Bioestatísticas: conceitos fundamentais e aplicações práticas

Resumos

A bioestatística ganha crescente importância e relevância nos últimos anos, sendo um dos principais pilares da investigação científica. Possui uma série de conceitos e regras que devem ser bem compreendidos para se realizar ou analisar um artigo. Nesta revisão são abordadas algumas das principais ferramentas utilizadas nos trabalhos de interesse da área oftalmológica, suas aplicações e limitações.

Bioestatística/métodos; Distribuições estatísticas; Interpretação estatística de dados

The biostatistics has gained significant importance in recent years, being one of the mainstays of current scientific research. It has a series of concepts and rules that must be understood to carry out or analyze an article. In this review we will discuss some of main tools utilized in works of interest in ophthalmology, its applications and limitations.

Biostatistics/methods; Statistical distributions; Data Interpretation, statistical

Introdução

O advento da Medicina Baseada em Evidências determinou novos padrões e exigências, o que marcou uma importante mudança na prática médica. A obtenção de conhecimento deixou de ser baseada apenas na sempre importante, mas limitada, experiência clínica, para ser adquirida por meio de metodologia científica. Esta envolve, de forma fundamental, o emprego de análise estatística⁽¹⁾. Com isso, o conhecimento em Bioestatística é habilidade fundamental para se realizar, avaliar ou interpretar adequadamente um trabalho científico. Entretanto, tal área representa um campo de dificuldades e preconceitos para o médico. Nesta revisão, abordamos de forma prática alguns dos principais testes para estudos de interesse em Oftalmologia.

Teste de hipóteses

Ao realizar um teste estatístico, em primeiro lugar, elaboramos hipóteses. Por exemplo, ao avaliarmos se espessura corneana central (ECC), espessura no ponto mais fino (EPMF) e valores de ceratometria central (K1 e K2) podem ser utilizados para diferenciar olhos normais de olhos com ceratocone, formulamos duas hipóteses. A hipótese de não haver diferença nos valores destas variáveis entre os grupos, chamada de hipótese nula (H₀). E a hipótese alternativa (H₁), que assume haver diferença entre os grupos normal e com ceratocone.

Amostras

Para iniciarmos o teste proposto é necessário estabelecer as amostras de investigação. Para que os resultados do trabalho sejam válidos é imprescindível que a amostra em cada grupo represente, da forma mais fidedigna possível, os diversos matizes da população. Entre as características mais relevantes da amostra devemos considerar sua forma de obtenção, tamanho, distribuição de suas variáveis e pareamento. Assim, podemos identificar potenciais fontes de viés e escolher a melhor metodologia e os melhores testes estatísticos para contorná-los.

Distribuição da amostra

A distribuição da amostra deve ser testada para verificar se ela é ou não paramétrica. Os testes estatísticos são altamente dependentes do tipo de distribuição dos valores obtidos na amostra. A distribuição normal ou gaussiana (paramétrica) é uma das formas de distribuição mais estudadas em bioestatística. Ela é definida por dois parâmetros: a média (µ) e a variância (σ²). Dentre as suas características observamos o formato em sino simétrico ao redor do centro, a presença de dois pontos de inflexão, um à direita e outro à esquerda, cuja distância do centro corresponde ao desvio padrão ou "sigma" (σ). Com estes dados, é possível calcular as probabilidades relacionadas a uma variável contínua com essa distribuição⁽²⁾.

Quando a amostra é relativamente grande, podemos aplicar o teorema do limite central e inferir a normalidade de sua distribuição. Esse teorema afirma que quando o tamanho de uma amostra aumenta, a distribuição amostral da sua média aproxima-se cada vez mais de uma distribuição normal⁽³⁾.

Entretanto, testes de aderência à normalidade podem ser utilizados. Entre eles, temos o teste de Kolmogorov-Smirnov, o teste de Lillefors, o teste de Shapiro-Wilk. Este último inicialmente descrito para amostras pequenas⁽⁴⁾. Nesses testes busca-se encontrar a hipótese nula, na qual não existe diferença entre a distribuição da amostra estudada e a distribuição normal. De forma geral, estes testes são bastante rigorosos e facilmente rejeitam a hipótese de Normalidade.

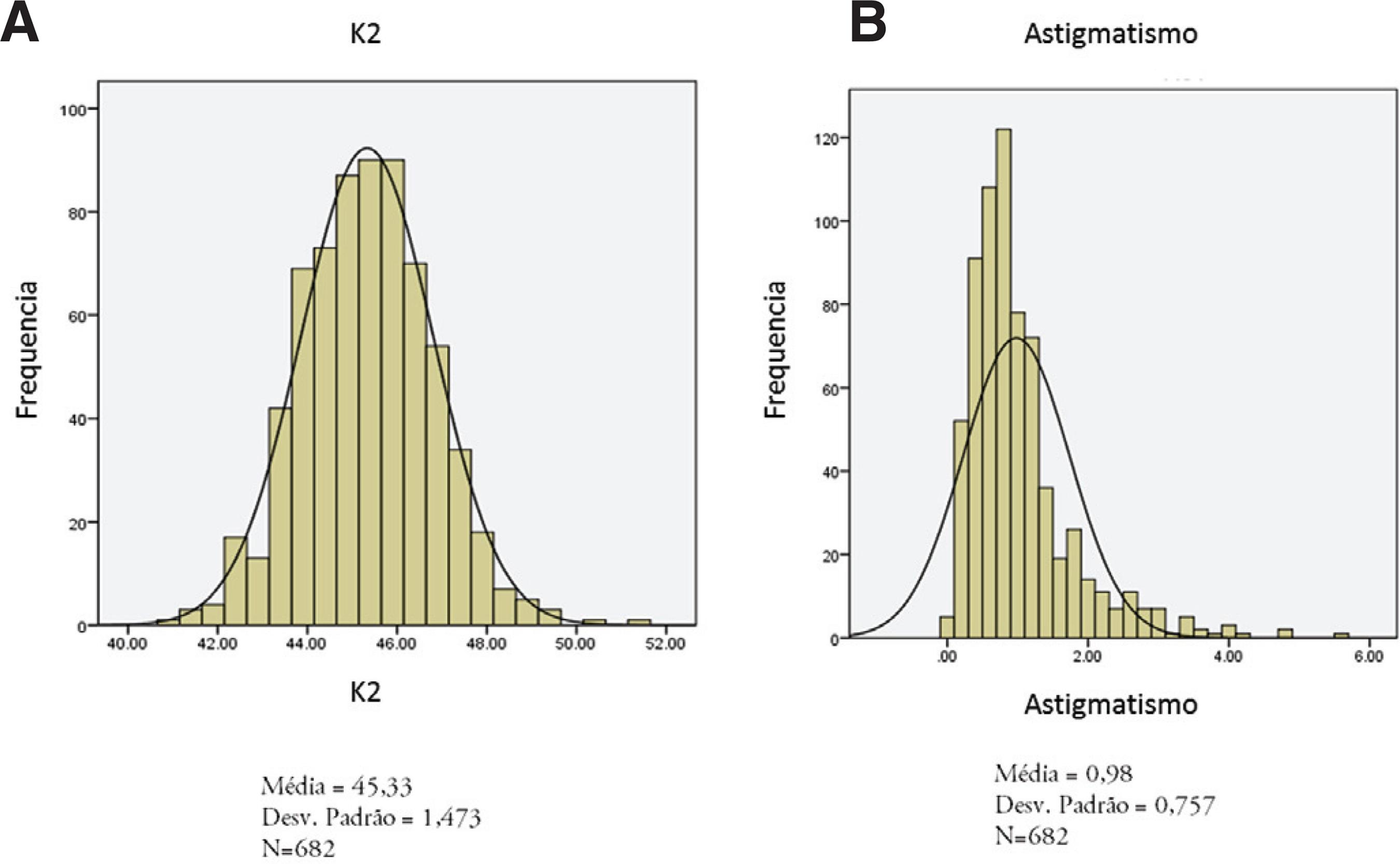
Outras ferramentas que podem ser utilizadas são os métodos descritivos, como a análise de histogramas (figura 1), coeficientes de assimetria e curtose. Quando a normalidade não pode ser inferida podemos utilizar testes não paramétricos ou realizar a transformação dos dados. A transformação mais comumente empregada é a transformação logarítmica cuja principal indicação é a assimetria dos dados. Outras transformações, como a raiz quadrada ou a recíproca também podem ser utilizadas em casos determinados⁽⁵⁾.

Figura 1
Histogramas. A: histograma de distribuição normal de K2 em pacientes com córneas saudáveis; B: histograma de distribuição não-normal de astigmatismo corneano em pacientes com córneas saudáveis

Amostras dependentes e independentes

Para escolhermos o tipo de teste a ser empregado, outra característica da amostra deve também ser considerada: se ela é pareada (dependente) ou não-pareada (independente). Um estudo com amostras pareadas ocorre quando cada observação no primeiro grupo for pareada com a mesma observação no segundo grupo. Em oftalmologia esse tipo de estudo é mais frequentemente empregado em casos em que há a observação da mesma amostra em dois ou mais tempos distintos, como o pré e o pós-operatório. Nesse caso, os dois grupos são compostos pelos mesmos indivíduos.

Nos casos não pareados, cada grupo é composto por indivíduos distintos, assim podemos comparar, por exemplo, grupos de saudáveis com grupos de portadores de alguma doença.

É importante ressaltar essa característica da amostra, pois duas observações em um mesmo indivíduo são mais prováveis de serem semelhantes que duas observações em dois indivíduos diferentes e, portanto, estatisticamente dependentes. Isso deve ser considerado pelo teste empregado para encontrar a validade estatística da diferença encontrada entre essas amostras.

Outra implicação do pareamento é o fato de os olhos serem órgãos pares. Existe uma simetria entre o olho direito e o esquerdo de um mesmo indivíduo. Se forem utilizados ambos os olhos de um paciente, poderão estar sendo mesclados dados dependentes com independentes, criando assim um erro metodológico⁽⁶⁾. Dessa forma, utilizar apenas um olho de cada paciente escolhido de forma aleatória é uma boa maneira de se realizar os estudos⁽⁷⁾.

Tipos de testes

Os testes estatísticos deverão obedecer às características da amostra citadas anteriormente: distribuição e pareamento. Entretanto, para escolha do melhor teste a ser empregado devemos considerar a quantidade de grupos ou observações. Os principais testes para cada situação estão resumidos no esquema 1.

Esquema 1

Exemplo de estudo

No exemplo a seguir vamos considerar a comparação de dois grupos. As amostras consistem em um olho randomicamente selecionado de 114 olhos normais e 44 casos de ceratocone⁽⁸⁾. O próximo passo é estabelecer as variáveis que serão estudadas. Considerando o objetivo de avaliar a capacidade de uma variável como teste diagnóstico, devemos testar se as diferenças entre os grupos são significantes. Sabendo-se que as amostras não são pareadas, a escolha do teste deve ser feita considerando-se a existência ou não de distribuição normal (paramétrica). Este teste confirma se a diferença não seria fruto do acaso. Um teste, como o de Kolmogorov-Smirnov deve ser realizado para verificar se as variáveis em cada grupo apresentam distribuição normal (com p>0,05), ou seja, ausência de diferença estatisticamente significante entre a distribuição dos dados na amostra e a distribuição normal. Histogramas também podem ser realizados para visualizar a distribuição em sino ou gaussiana.

O teste t de Student pode ser utilizado se ambas as amostras são paramétricas. De acordo com o teorema do limite central, por se tratar de amostra grande com mais de 30 indivíduos, a utilização do teste paramétrico a priori já poderia ser considerada como "correta". Entretanto, se a amostra fosse pequena e a normalidade não fosse verificada, poderíamos como mencionado anteriormente recorrer à transformação dos dados ou utilizar um teste não paramétrico. O teste não paramétrico como o de Mann-Whitney (Mann-Whitney U test ou Wilcoxonrank-sum test) seria uma boa alternativa.

Ao realizar a prova paramétricapara as variáveis K1, K2, ECC e EPMF, encontramos valor p (probabilidade de erro ao concluir que existe diferença estatisticamente significante) inferior a 0,001 (tabela 1), o que confirma haver diferença com significância estatística entre olhos normais e com ceratocone em cada uma dessas variáveis. Quando o mesmo teste é realizado para o eixo do astigmatismo encontramos p=0,12, ou seja, 12% de probabilidade de erro ao concluir que existe diferença significativa entre as duas amostras. Em geral, considera-se estatisticamente significante, uma chance de 5% de a diferença encontrada na amostra não representar uma diferença real existente entre as populações, ter sido apenas fruto do acaso. Dessa forma, devido a essa elevada margem de erro, consideramos não haver diferença estatisticamente significante nessa variável entre as duas populações (tabela 1).

Tabela 1
Diferenças entre grupos

	Normais			Ceratocone
	Média ± Desvio Padrão	Intervalo		Média ± Desvio Padrão	Intervalo	p valor*
K1	42.68 ± 1.47	39.5 - 46.7		49.35 ± 7.64	38.6 - 71.6	< 0.001
K2	43.66 ± 1.58	39.8 - 48.2		51.58 ± 9.1	42.6 - 77.5	<0.001
ECC	550 ± 35	444 - 632		460 ± 57	283 - 548	<0.001
EPMF	544 ± 35	443 - 629		443 ± 60	254 - 542	<0.001
Eixo Astig	97 ± 71	1 - 180		76 ± 64	0 - 179	0.12

• ^(*)
  Teste t de Student

Os gráficos Box-Plot e Dot-Plot (figura 2) ilustram a distribuição dos valores da ECC nos grupos normal e ceratocone. Nesses gráficos, podemos verificar que apesar de existir diferença significante entre os grupos, existe grande sobreposição dos seus valores, o que impossibilita separá-los por completo. Isso faz com que a aplicação desta variável seja limitada para diferenciar ou classificar olhos normais e com ceratocone, essa sobreposição provoca uma maior chance de erros.

Figura 2
Gráficos Box-Plot e Dot-Plot da distribuição da ECC

Erros de classificação e ponto de corte

Ao se classificar ou tentar diferenciar olhos normais e com ceratocone, utilizando variáveis tais como os valores da ECC, podem acontecer dois tipos de erro. O erro do tipo I ou α está relacionado com um resultado positivo no grupo de olhos classificados como normais, ou resultado falso positivo. O erro do tipo II ou β representa a possibilidade de um caso no grupo de olhos classificados como doentes ter um resultado negativo, o que é denominado um falso negativo (tabela 2).

Tabela 2
Resultados de um teste diagnóstico

Teste	Grupo Doente	Grupo Normal (sem doença)
Positivo para Doença	Decisão correta	Erro do tipo II
	Verdadeiro	ou β Falso
	Positivo (VP)	Negativo (FN)
Negativo para Doença	Erro do tipo I	Decisão correta
	ou α Falso	Verdadeiro
	Positivo (FP)	Negativo (VN)

Entretanto, a determinação de "positividade" de um teste diagnóstico (ou classificador) depende fundamentalmente da determinação de um ponto de corte. Considerando a variável em questão, apresentar-se como uma variável quantitativa contínua ou ordinal, cada valor pode ser testado como corte para determinar a presença ou ausência de doença. Por exemplo, se considerarmos o ponto de corte para ECC de 540µm (abaixo de 540µm=ceratocone), 37 (32,4%) dos 114 olhos com córneas normais apresentariam erro tipo I ou α, enquanto apenas um caso com ceratocone apresentaria erro do tipo II ou β. Desta forma podemos calcular a sensibilidade e a especificidade hipotéticas do teste, com cada possível valor de ponto de corte testado (tabela 3).

Tabela 3
Sensibilidade e Especificidade de cada ponto de corte

Ponto de Corte	Sensibilidade (%)	Especificidade (%)
< 283	0	100
<= 435	20.45	100
<= 444	20.45	99.12
<= 456	34.09	99.12
<= 459	34.09	98.25
<= 460	36.36	98.25
<= 462	36.36	97.37
<= 477	61.36	97.37
<= 479	63.64	96.49
<= 483	63.64	95.61
<= 493	68.18	95.61
<= 496	68.18	93.86
<= 498	72.73	93.86
<= 501	72.73	91.23
<= 502	75	91.23
<= 504	77.27	90.35
<= 505	79.55	88.6
<= 506	79.55	87.72
<= 507	81.82	87.72
<= 508	81.82	86.84
<= 509	88.64	85.96
<= 516	93.18	85.96
<= 523	93.18	78.07
<= 524	95.45	77.19
<= 529	95.45	72.81
<= 532	97.73	71.05
<= 547	97.73	53.51
<= 548	100	53.51
<= 632	100	0

Sensibilidade e especificidade

Sensibilidade é a probabilidade de um teste apresentar resultado positivo em um indivíduo acometido por uma doença, sendo calculada utilizando-se apenas os indivíduos doentes, como a razão entre os casos doentes com resultado positivo (VP - verdadeiro positivo) sobre o total de doentes que inclui também os casos falso-negativos (FN).

$\mathit{Sensibilidade}=\frac{\mathit{VP}}{\left(\mathit{VP}+\mathit{FN}\right)}$

Especificidade é definida como a probabilidade do teste apresentar resultado negativo em paciente sem doença, sendo calculada utilizando-se apenas os indivíduos sem doença, como a razão entre os casos não doentes com resultado negativo (VN - verdadeiro negativo) sobre o total de não doentes que inclui os casos falso positivos (FP).

$\mathit{Especificidade}=\frac{\mathit{VN}}{\left(\mathit{VN}+\mathit{FP}\right)}$

Os conceitos de sensibilidade e especificidade serão utilizados, a seguir, para descrever quantitativamente o desempenho de um teste diagnóstico por meio da construção de sua respectiva curva ROC.

Curva ROC1 e Acurácia de um teste

A curva ROC é construída em um plano cartesiano. No eixo Y encontra-se a sensibilidade e no eixo X, 1 menos a especificidade (1-E), ambos em valores decimais. Para cada ponto de corte utilizado pelo teste são calculadas a sensibilidade e a especificidade e inserido um ponto no gráfico. A união desses pontos forma a curva ROC.

No caso da ECC, o melhor ponto de corte foi 517µm, com sensibilidade de 86% e especificidade de 93,2%. A respectiva curva ROC pode ser visualizada na figura 3.

Figura 3
Curva ROC e ponto de corte para ECC normais versus ceratocone

A área sob a curva (AUC²) representa a acurácia ou performance global do teste, pois leva em consideração todos os valores de sensibilidade e especificidade para cada valor da variável do teste. Quanto maior o poder do teste em discriminar os indivíduos doentes e não doentes, mais a curva se aproxima do canto superior esquerdo, no ponto que representa a sensibilidade e 1-especificidade do melhor valor de corte. Quanto melhor o teste, mais a área sob a curva ROC se aproxima de 1. Um teste com pequeno poder diagnóstico tem curvas mais retilíneas. Um teste que represente simplesmente o acaso (como jogar uma moeda para alto e obter resultados binários aleatórios) teria cerca de 50% de chance de positivo e 50% de chance de negativo, independente do grupo em que esteja, tem área sob a curva bem próxima de 0,50 (figura 4).

Figura 4
Áreas sob a curva ROC

Comparação das áreas sob as curvas ROC

Após estabelecida a diferença estatisticamente significante entre as variáveis de pacientes saudáveis e doentes é preciso estabelecer se esse teste tem boa acurácia no diagnóstico. Conforme visto anteriormente podemos fazê-lo construindo uma curva ROC e estabelecendo o melhor ponto de corte.

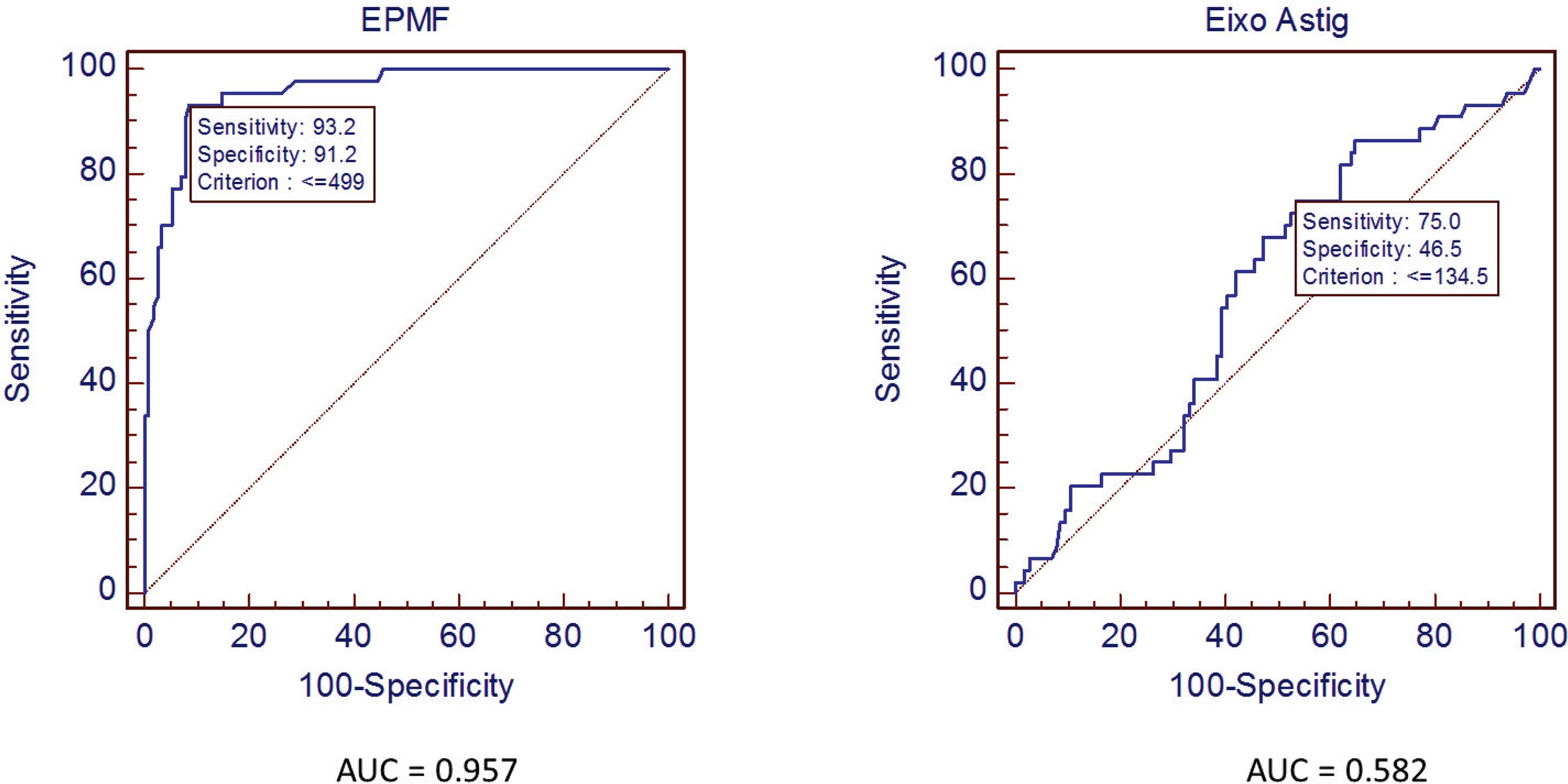
Se temos dois métodos para diagnóstico distintos, podemos compará-los utilizando a área sob a curva ROC. Para sabermos se a diferença entre elas é estatisticamente significativa devemos utilizar um teste que as compare, como por exemplo o teste de DeLong⁽⁹⁾. No exemplo anterior quando construímos as curvas ROC para as variáveis K1, K2, ECC e EPMF, observamos que os índices de espessura apresentam melhor desempenho que os de curvatura citados. Entre eles a AUC da EPMF (0.957) é maior que da ECC (0.939). A sua comparação com o teste de DeLong apresenta p=0.003, demonstrando que a maior acurácia da espessura medida no ponto mais fino é estatisticamente significante. Os resultados são resumidos na figura 5 e nas tabelas 4 e 5.

Figura 5
Comparação entre as curvas ROC

Tabela 4
Área sob a curva ROC

		AUC
K1		0.865
K2		0.859
ECC		0.939
EPMF		0.957

Tabela 5
Comparação par a par da AUC com método de DeLong (p-valores)

	K1	K2	ECC	EPMF
K1		0.85	0.049	0.036
K2			0.037	0.009
ECC				0.003
EPMF

Significância estatística versus significância clínica

Para verificarmos se a diferença encontrada em um teste diagnóstico possui significância estatística buscamos o valor p ou p-valor, denominado o nível descritivo, que tem relação direta com o poder do teste. Pode ser definido como a "probabilidade mínima de erro ao concluir que existe significância estatística"⁽¹⁰⁾.

Um resultado é dito estatisticamente significante quando o p-valor encontrado é menor que o erro tipo I estabelecido como "aceitável", em geral 0,05 (5% de chance de erro, ou seja, de concluir que a diferença encontrada é significativa quando na realidade reflete apenas o acaso).

Significância estatística, entretanto, não é necessariamente o mesmo que significância clínica. O p-valor é influenciado pelo tamanho da amostra. Amostras grandes tendem a apresentar p-valor pequeno, com menor significância prática de seus resultados. Por outro lado, amostras pequenas podem afetar o p-valor, de modo que fique mais alto.

Nesse caso, apesar de haver relevância clínica, devido ao tamanho inadequado da amostra, há uma interpretação equivocada dos resultados⁽¹¹⁾. O valor p, portanto, não determinará a acurácia de um teste, mas sim, como dito anteriormente, a AUC.

Intervalo de confiança

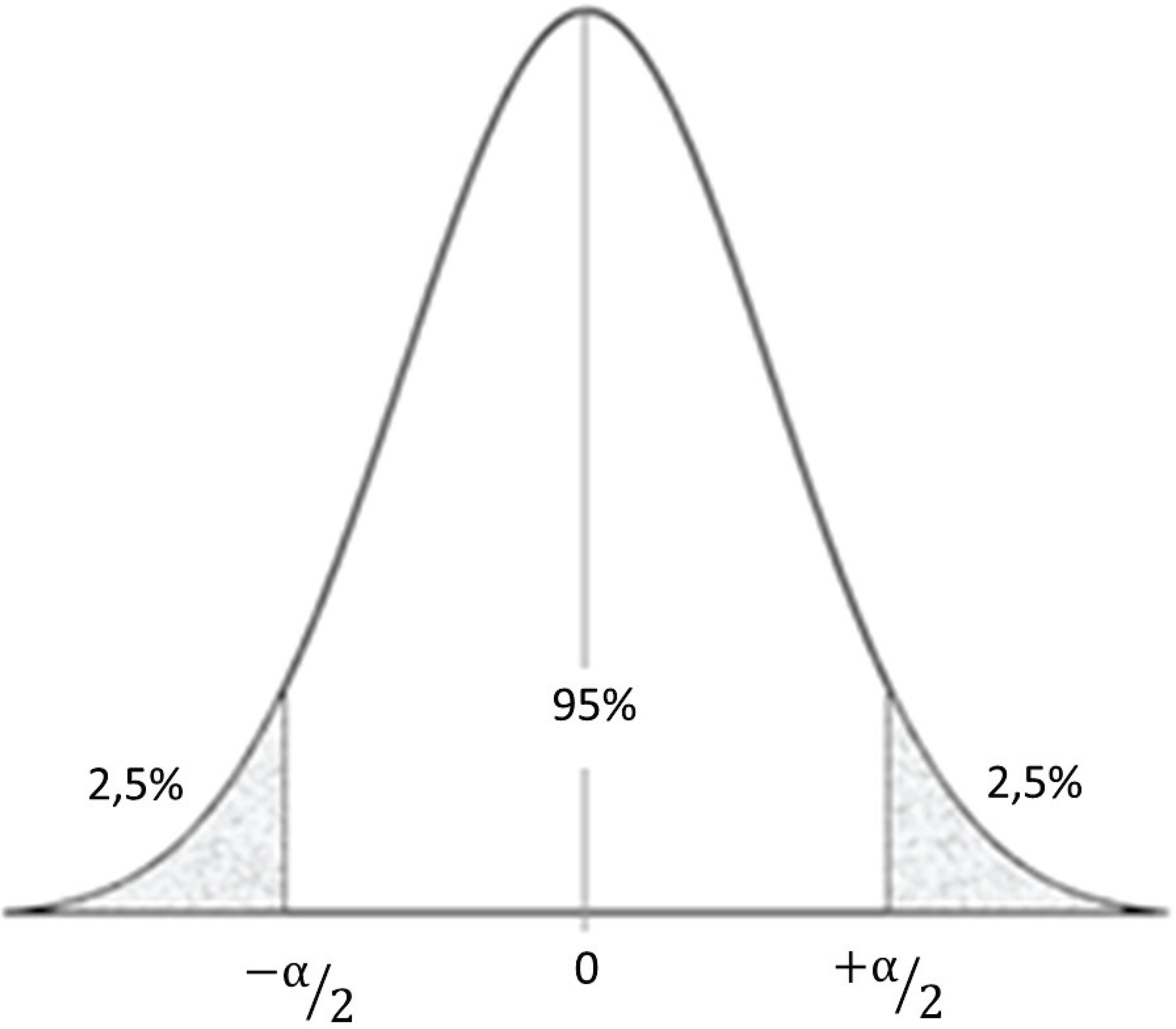
O conceito de intervalo de confiança está relacionado com a variabilidade das estimativas de acurácia. O seu cálculo está diretamente relacionado com o erro tipo I ou α, como pode ser visualizado na figura 6. Quanto menor o α, mais amplo o intervalo de confiança, ou seja, mais confiável aquele estimador. No exemplo da figura 6 em um teste bicaudal o α escolhido foi 5%. Então, com probabilidade de 95%, o valor estará dentro do intervalo entre - α/2 e +α/2. Tanto o intervalo de confiança como o erro padrão são calculados de acordo com as características e resultados obtidos nas amostras, servindo para interpretação da relevância clínica do variável diagnóstica⁽¹²⁾.

Figura 6
Intervalo de confiança em um teste bicaudal, α=5%

Aprimoramento das ferramentas diagnósticas

Enquanto os valores de curvatura corneana centrais (K1 e K2) e a ECC, não podem ser utilizados isoladamente para separar normais de ceratocone, outras variáveis derivadas do estudo tomográfico podem ser considerados de forma isolada ou combinada⁽¹³⁾.O mapa de curvatura topométrico nos fornece o dado do ponto mais curvo da superfície anterior. Esse índice apresenta maior acurácia (AUC maior) que os índices de curvatura central. No mapa tomográfico de espessura podemos obter a EPMF, que, como visto anteriormente, representa uma melhora na capacidade de detecção de ceratocone quando comparada à ECC.

Combinação de variáveis

Para aumentarmos ainda mais a acurácia no diagnóstico, podemos combinar diferentes variáveis. Essa combinação pode ser feita através de uma operação matemática fundamental como é o caso do Ambrósio's Relational Thickness (ART), que representa a razão da espessura corneana no ponto mais fino pela progressão paquimétrica. Tal índice demonstrou elevado poder diagnóstico na detecção do ceratocone⁽⁸⁾.

Outras formas mais sofisticadas de se combinar variáveis são a análise discriminante linear e a regressão logística, que a partir de um conjunto de variáveis, de maneira ponderada, é capaz de separar os indivíduos em grupos. Esse tipo de combinação tem grande valor em testes diagnósticos, pois pode separar com mais precisão os indivíduos normais dos doentes por meio dos diversos dados obtidos nos testes.

Com as amostras citadas anteriormente podemos realizar uma regressão logística incluindo os dados dos estudos dos mapas topográfico (Kmáx) e tomográfico (EPMF). Obtermos a fórmula:

- 960,27 + 44,29 * Kmax - 2,27 * EMPF

A partir dessa fórmula calculamos o valor para cada um dos indivíduos da amostra e obtemos uma nova variável. Ao construir os gráficos Box-Plot e Dot-Plot e a curva ROC, observamos uma separação perfeita entre os grupos, como visto na figura 7. Entretanto, fórmulas obtidas por meio desses métodos devem ser validadas em outras amostras para ter sua aplicabilidade comprovada nas mais diversas populações.

Figura 7
Gráficos Dot-Plot, Box-Plot da regressão logística (RL) criada a partir de Kmax e EPMF e curva ROC com máxima aproximação do canto superior esquerdo (normal: n=114, ceratocone: n=44)

Outras formas ainda mais sofisticadas como os complexos algoritmos de inteligência artificial tem sido implementados no estudo das patologias oftalmológicas. Já foi demonstrado que tal método aumenta consideravelmente a eficácia na detecção de doenças^(14,15).

Conclusão

Buscamos com essa revisão citar os principais conceitos em bioestatística e alguns testes para análise dos resultados de um estudo científico e sua aplicabilidade. Por ser um tema bastante amplo, não pretendemos com esse texto esgotá-lo, mas apenas estabelecer um guia para o seu estudo dada a importância do tema para a prática médica.

De fato, com o grande volume de informações gerado diariamente, é necessário chamar a atenção dos oftalmologistas para a bioestatística, pois a análise crítica das estatísticas com as quais o profissional da área médica se depara é de fundamental relevância para a melhora da sua prática.

Referências

• ¹
  El Dib RP. [How to practice evidence-based medicine]. J Vasc Bras. 2007;6(1):1-4. Editorial. Portuguese.
• ²
  Abrão FP, Araújo WA, Vieira GM. [Tonometer calibration in Brasília, Brazil]. Arq Bras Oftalmol. 2009;72(3):346-50. Portuguese.
• ³
  Altman DG, Bland JM. Statistics notes: the normal distribution. BMJ. 1995;310(6975):298.
• ⁴
  Flynn MR. Analysis of censored exposure data by constrained maximization of the Shapiro-Wilk W statistic. Ann Occup Hyg. 2010;54(3):263-71.
• ⁵
  Bland JM, Altman DG. Transformations, means, and confidence intervals. BMJ. 1996;312(7038):1079.
• ⁶
  Holopigian K, Bach M. A primer on common statistical errors in clinical ophthalmology. Doc Ophthalmol. 2010;121(3):215-22.cReview.
• ⁷
  Altman DG, Bland JM. Statistics notes. Treatment allocation in controlled trials: why randomise? BMJ. 1999;318(7192):1209. Review.
• ⁸
  Ambrósio R Jr, Caiado AL, Guerra FP, Louzada R, Roy AS, Luz A, et al. Novel pachymetric parameters based on corneal tomography for diagnosing keratoconus. J Refract Surg. 2011;27(10):753-8.
• ⁹
  DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988;44(3):837-45.
• ¹⁰
  Paes ÂT. Itens essenciais em bioestatística. Arq Bras Cardiol. 1998;71(4):575-80.
• ¹¹
  Altman DG, Bland JM. Absence of evidence is not evidence of absence. BMJ. 1995;311(7003):485.
• ¹²
  Azeredo AP. Prestígio clínico da estatística. Rev Bras Oftalmol. 2007;66(6):367-8. Editorial.
• ¹³
  Ambrósio R Jr, Belin MW. Imaging of the cornea: topography vs tomography. J Refract Surg. 2010;26(11):847-9.
• ¹⁴
  Maeda N, Klyce SD, Smolek MK. Neural network classification of corneal topography. Preliminary demonstration. Invest Ophthalmol Vis Sci. 1995;36(7):1327-35. Erratum in: Invest Ophthalmol Vis Sci 1995;36(10):1947-8.
• ¹⁵
  Lyra JM, Machado AP, Ventura BV, Ribeiro G, Araújo LP, Ramos I, et al. Applications of artificial intelligence techniques for improving tomographic screening for ectasia. In: Belin MW, Khachikian SS, Ambrósio Jr R. Elevation based corneal tomography. City of Knowledge: Jaypee Highlights Medical Publishers; 2012. p.123-36.

Datas de Publicação

• Publicação nesta coleção
  Jan-Feb 2014

Histórico

• Recebido
  23 Set 2013
• Aceito
  16 Out 2013