Variable phase equation in quantum scattering

Equação da fase variável no espalhamento quântico

ARTIGOS GERAIS

Variable phase equation in quantum scattering

Equação da fase variável no espalhamento quântico

Vitor D. Viterbo^I; Nelson H.T. LemesII, ¹; João P. Braga^I

^IDepartamento de Química, Universidade Federal de Minas Gerais, Belo Horizonte, MG, Brasil

^IIInstituto de Química, Universidade Federal de Alfenas, Alfenas, MG, Brasil

ABSTRACT

This paper presents the derivation and applications of the variable phase equation for single channel quantum scattering. The approach was first presented in 1933 by Morse and Allis and is based on a modification of the Schrödinger equation to a first order differential equation, appropriate to the scattering problem. The dependence of phase shift on angular momentum and energy, together with Levinson's theorem, is discussed. Because the variable phase equation method is easy to program it can be further explored in an introductory quantum mechanics course.

Keywords: phase equation, scattering matrix, phase shift.

RESUMO

Este artigo apresenta a dedução e aplicações da equação da fase variável para o caso de um canal no espalhamento quântico. Esta abordagem foi apresentada pela primeira vez em 1933 por Morse e Allis e baseia-se numa modificação da equação Schrödinger para uma equação diferencial de primeira ordem, adequada para o problema de espalhamento. A dependência do deslocamento de fase com o momento angular e a energia, juntamente com o teorema de Levinson, é discutida. A equação resultante do método da fase variável é de fácil programação e pode ser explorado em cursos introdutórios de mecânica quântica.

Palavras-chave: equação da fase, matriz de espalhamento, deslocamento de fase.

1 Introduction

The variable phase method was first introduced in 1933 by Morse and Allis [1] who established the basic equation for zero angular momentum scattering. In 1949, Drukarev extended their results in the book "The Theory of Electron-Atom Collision" [2]. In this book, the method was established in a more general form for angular momentum different from zero. A presentation of this method is given by F. Calogero [3] in his 1967 book, although the simplicity of the method is not fully explored. The present discussion will be based on a single channel problem, but the method can be generalised to several channels [3, 4]. The variable phase method has been used before in several applications, such as in detection of bound and meta-stable states [5].

Due to its simplicity, the variable phase method represents an attractive tool, both for the theoretical and numerical understanding of the scattering process. The objective of the present work is to emphasise this simplicity. The original Morse and Allis [1] derivation for zero angular momentum can be adequately adapted for any angular momentum, as will be discussed. There will be no need to apply boundary conditions or to calculate Bessel functions. This simplifies the approach considerably, presenting a very efficient and straightforward approach to elastic scattering. Numerical examples will be considered for model potential energy functions, together with the angular momentum and energy dependence for the phase shift. A discussion of the Levinson theorem will also be carried out.

2 Basic quantum scattering theory

In a central field collision process, one can seek a solution of the Schrödinger equation by expressing the total wavefunction as partial waves,

in which are the Legendre polynomials. If the interaction between the particles is described by a potential energy function , it is appropriate to define an effective potential, , with h the Planck's constant, µ the system reduced mass's, R the scattering coordinate and l the angular momentum. Substitution of Eq. (1) into Schrödinger equation then gives for

For a given potential energy function one has to find the solution . Because this potential energy function goes to zero at large distances, the appropriate boundary condition will be

in which S is the scattering matrix, , where denotes the phase shift. The phase shift, or the scattering matrix, gives complete information about the collision process, including the differential and total cross sections. The relation between the phase shift and cross section can be found in quantum scattering textbooks [6, 7].

The theoretical information about a collision process is completely described by the scattering matrix or phase shift. In a time independent formalism, this scattering matrix is calculated in a three steps procedure, involving the following: a) initial conditions for the wavefunction; b) numerical solution of the Schrödinger equation and c) boundary conditions with Bessel functions at the end point. There are a variety of methods to solve the Schrödinger equation, and a comparison between two common algorithms, log-derivatives and Numerov methods [8], is presented in the literature. These numerical procedures are simplified by using an important scattering matrix property: the matrix S is a ratio of amplitudes, and the overall wavefunction normalisation is irrelevant, a fact made clear in Eq. (3). This is an important point to be explored in the variable phase approach.

3 The variable phase equation

In the variable phase approach, the potential energy function is divided into two regions as

In an analogous way, the solution is considered in these two regions as . This method seeks the solution φ(R), because the solution for corresponds to a free particle wavefunction conveniently written as

The amplitude and phase for this free particle solution will carry information about the inner region and, as a consequence, must depend on .

From Schrödinger equation one obtains for the log-derivative wavefunction,

Using Eq. (5) one can develop

or (using cos²x = 1 - sin²x),

which is the variable phase equation for the one-dimensional case. This is essentially the Morse and Allis deduction but is developed here for the effective potential considering angular momentum different from zero. This extremely simple proof will be enough to understand the basic concepts in elastic atomic collision.

Equation (8) requires an initial condition to be propagated. To avoid numerical instability, it is convenient to start integration at a point, R0, close to the origin. Assuming the wavefunction to be zero at this point and for zero angular momentum, one must satisfy u0(R0)= 0. From Eq. (3), it is clear that , which can be used as an initial condition. Changing the angular momentum to larger values will shift the potential energy function to the right, making this initial condition appropriate for any angular momentum. The initial condition is then

The phase shift calculated from Eq. (8) will also carry information about the centrifugal term. To clarify this point, consider the solution of Eq. (2) for a very large scattering coordinate, in a region with Ep(R) = 0. In this case, solutions will be given by the Riccati-Bessel function, with asymptotic behaviour of and . Consequently, solutions of the Schrödinger equation for zero potential energy will carry a phase of due to the centrifugal contribution. Therefore, the phase for the potential can be calculated from the phase shift for the potential by subtracting the centrifugal term contribution, . The required phase shift will be

Consequently, usage of the variable phase equation can be summarised by three equations,

Implementation of this approach can be performed in any computer language, for it will involve the numerical propagation of a first order differential equation.

4 Model potential

A Morse potential energy function [9],

with , and [10], which are approximate values for hydrogen-hydrogen interaction, will be used to illustrate the method. Units for energy are in as, for example, in the term. These units are obtained by first calculating energy in atomic units and then converting to .

This prototype potential energy function is meant to be a model potential and does not precisely describe the H2 molecule. In fact, any model potential can be used, as long as results are compared with a more precise calculation. This will be done here by comparing scattering matrix values calculated by the variable phase approach with those calculated by the Renormalized Numerov method [8, 11].

5 Results and discussion

Propagation of the variable phase equation for k² = 25 Å^-2 and several values of angular momentum will be discussed. The initial condition was taken at R0=10^-3 Å, but the final integration coordinate has to be tested against convergence. For example, for l = 0, the maximum scattering coordinate was R_max = 10 Å. For angular momentum different from zero, integration has to be carried out to large scattering coordinates, because one must approximately cancel the centrifugal contribution. The maximum integration point will depend on the angular momentum and can be estimated by imposing the condition , in which ε is a small number. For a typical value of ε = 10^-4 and l = 30, one obtains the maximum integration point at 3000 Å, which is the consequence if Bessel function boundary conditions are not considered.

Numerical integration was performed using a Runge-Kutta fifth and sixth order method with variable step size, as in Forsythe and Moler [12]. This variable step size is very important because for low collision energy, the phase shift will have a step function behaviour. Additionally, for large scattering coordinates, considerable computer time can be saved by using larger step sizes.

The reliability of the present approach can be inferred by comparing phase shifts with another more precise scheme. The scattering matrices calculated from the variable phase method and the very precise Renormalized Numerov method are presented in Table 1. The real and imaginary parts of the scattering matrix are given by . The results indicate that the variable phase method gives essentially exact answers and can be further explored.

Phase shift convergence against the scattering coordinate is shown in Fig. 1. If the potential is positive, the phase shift will be negative. From Eq. (8) one may infer the sign of the phase shift, because it is proportional to -Ep(R). If an approximation is used for the phase shift derivative, one can write that for Eq. (8), . Then, for a positive potential energy function, the phase shift, together with the initial condition, will give negative values. However, if the potential changes sign, the phase shift will also carry this information, as exemplified in Fig. 1. The potential energy function changes sign at R = 0.46 Å, exactly at the point at which the phase shift changes its behaviour. The constant phase shift value for large R, shown in Fig. 1, is also evident from Eq. (8). In this region, the potential energy function will go to negligible values and, consequently, .

As the angular momentum is increased, the centrifugal term will become more important, making the potential energy function negligible. Hence, the total potential for large angular momentum will be approximately given by the centrifugal contribution. In this case, phase shift must go to zero, because the reference potential in the present formulation is the centrifugal potential. In fact, that is the reason for subtracting the phase from the computed phase shift. At approximately l = 30, the phase shift goes to zero, and no more scattering processes can take place, as shown in Fig. 2. This maximum angular momentum can be estimated from a classical analysis. The maximum impact parameter, b, above which there will be no scattering, can be estimated to be equal to the potential range, . Because total angular momentum is given by , one has. Considering the potential range to be 6 Å one has , as confirmed numerically. Additionally, this maximum angular momentum estimation is important to calculate cross section because it will involve a summation on phase shifts for different angular momenta.

Oscillations in Fig. 2 can also be explored to clarify the connection between classical and quantum scattering. In a semiclassical context, the derivative of the phase shift is proportional to the scattering angle. For this reason, the maximum in Fig. 2 corresponds to a concentration of trajectories, and consequently, greater intensity in the differential cross section, an effect known as the rainbow effect in atomic and molecular collision [13].

Levinson's theorem [6] states that at the limit of zero collision energy the phase shift is a multiple of π,

in which n_b is the number of bound states that the molecule can support. If there are bound states with zero energy and angular momentum different from zero, then Eq. (13) has to be modified to [5,6]. As confirmed numerically, these bound states with zero energy were not detected here. Equation (13) is thus used in the present study.

Levinson's theorem is a powerful and elegant theorem that makes a connection between the continuum and the discrete states of system. The variable phase equation is appropriate to investigate this theorem numerically. Because the energy will be small, only zero angular momentum has to be considered. Numerical integration will provide information on the number of bound states, and because transitions in infrared spectra are due to vibrational mode excitation, one can infer consequences, such as the number of lines, about the infrared spectrum [10]. The results are shown in Table 2. There is a clear tendency to show that the prototype molecule can accommodate 14 bound states. In fact, at the limit for k²=10^-4 Ų, it was found that , confirming this tendency. Thus, the prototype potential represents a molecule with 14 bound states. This procedure is the same as the procedure adopted for a realist potential energy function and was used to detect bound and meta-stable states of rare gas hydrides [5].

Further theoretical and computational aspects of the method can be explored. For example, the first Born approximation [6] is a special case of the variable phase method. For small phase shift values, such that is a valid approximation, the phase differential equation reduces to

which is the first Born approximation in differential form. Integration of this differential equation gives the usual presentation for this approximation,

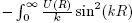.Thus, usage of the variable phase approach can provide a simple and convincing proof of the first Born approximation.

6 Conclusion

In contrast with numerical methods to calculate elastic scattering that require knowledge of Bessel functions, a simple approach based on the variable phase method was discussed. The algorithm discussed is very simple to implement and allows several important consequences to be explored. Calculation of the scattering matrices were conducted and compared with results obtained using the Renormalized Numerov method. Phase shift behaviour as a function of energy and angular momentum was discussed, together with numerical examples of Levinson's theorem.

The variable phase method as presented here can be explored further to calculate other quantum properties.

Acknowledgment

We would like to thank CNPq for financial support.

Recebido em 3/6/2013

Aceito em 6/9/2013

Publicado em 6/2/2014

• [1] P.M. Morse and W.P. Allis, Phys. Rev. 44, 269 (1933).
• [2] G.F. Drukarev, The theory of Electron-Atom Collision (Academic Press, London, 1965).
• [3] F. Calogero, Variable phase approach to potential scattering (Academic Press, New York, 1967).
• [4] R. Martinazzo, E. Bodo and F.A. Gianturco, Comput. Phys. Commun. 151, 187 (2003).
• [5] J. P. Braga and J.N. Murrell, Molecular Physics 53, 295 (1984).
• [6] C.J. Joachain, Quantum collision theory (North-Holland, Amsterdam, 1975).
• [7] J.N. Murrell and S.D. Bosanac, Introduction to the Theory of Atomic and Molecular Collisions (John Wiley, Chichester, 1989).
• [8] J.P. Braga, J. Comput. Chem. 10, 413 (1989).
• [9] P.M. Morse, Phys. Rev. 34, 57 (1929).
• [10] G. Herzberg, Molecular Spectra and Molecular Structure (Van Nostrand Reinhold, New York, 1950).
• [11] B.R. Johnson, J. Chem. Phys. 67, 4086 (1977).
• [12] G.E. Forsythe, M.A. Malcolm and C.B. Moler, Computer Methods for Mathematical Computations (Prentice-Hall, Englewood Cliffs, 1977).
• [13] J.R. Pliego, J.P. Braga and S.D. Bosanac, Phys. Rev. A 52, 342 (1995).

Publication Dates

• Publication in this collection
  29 Apr 2014
• Date of issue
  Mar 2014

History

• Received
  03 June 2013
• Accepted
  06 Sept 2013