Geometria fractal: propriedades e características de fractais ideais

Fractal geometry: properties and features of ideal fractals

ARTIGOS GERAIS

Geometria fractal: propriedades e características de fractais ideais

Fractal geometry: properties and features of ideal fractals

Thiago Albuquerque de Assis^I; José Garcia Vivas Miranda^II; Fernando de Brito Mota^II; Roberto Fernandes Silva Andrade^II; Caio Mário Castro de Castilho^II,1

^IGrupo de Sistemas Complejos, Departamento de Física y Mecánica ETSI Agrónomos, Universidad Politécnica de Madrid, Madrid, España

^IIInstituto de Física, Universidade Federal da Bahia, Salvador, BA, Brasil

RESUMO

Descobertas recentes revelam que modelos matemáticos euclidianos, de há muito estabelecidos e que procuram reproduzir a geometria da natureza, às vezes se apresentam incompletos e, em determinadas situações, inadequados. Especificamente, muitas das formas encontradas na natureza não são círculos, triângulos, esferas, icosaedros ou retângulos. Enfim, não são simples curvas, superfícies ou sólidos, conforme definidos na geometria clássica de Euclides (300 a.C), cujos teoremas possuem lugar de destaque nos textos de geometria. Neste trabalho apresenta-se uma breve e elementar, mas que busca ser consistente, discussão sobre algumas definições e aplicações relacionadas à geometria fractal, em particular fractais ideais. Caracterizaremos alguns fractais auto-similares que, por sua importância histórica ou riqueza de características, constituem exemplos ilustrativos "clássicos" de propriedades de fractais, propriedades estas que muitas vezes aparecem dispersas numa literatura mais especializada. Mostra-se, por construção, que suas medidas de comprimento, área e volume, nas dimensões euclidianas usuais, dão margem a resultados contraditórios. Estes podem ser explicados pelo fato de que tais objetos só podem ser adequadamente mensurados em espaços de dimensão fracionária.

Palavras-chave: fractais, auto-similaridade, dimensão fractal.

ABSTRACT

Recent discoveries reveal that mathematical models, established a long time ago and searching to reproduce the nature's geometry, sometimes result being incomplete and even inadequate in some situations. Specifically, many of the forms found in the nature are not circles, triangles, spheres, icosahedrons or rectangles. Finally, they are not simple curves, surfaces or solids, as defined in the classical geometry of Euclides (300 b.C), whose theorems possesses a prominent place in the geometry texts. In this work a brief and elementary, although intended to be consistent, discussion about some definitions and applications related to the fractal geometry is presented. It is also presented properties of some fractals that, for its historical importance or wealth of characteristics, constitute "classical" illustrative examples of the fractals properties which, despite this, many times appear dispersed in the specialized literature. It is shown, by construction, that the measures of length, area and volume for these objects, within the usual Euclidean dimensions, lead to contradictory results. This can be explained by considering that these objects can be adequately measured using spaces of fractional dimensions.

Keywords: fractals, self-similarity, fractal dimension.

1. Introdução

O emprego do termo fractal pode ser temporalmente localizado no ano de 1975, quando Benoit Mandelbrot pela primeira vez dele fez uso. Quando, na iminência da completude da sua primeira grande obra sobre o assunto [1], Benoit Mandelbrot sentiu a necessidade de encontrar um nome para descrever a geometria com que buscava representar as reais formas da natureza. Uma consulta a um dicionário de latim resultou no encontro do adjetivo fractus, do verbo frangere, que significa quebrar.² Foi assim criada a palavra fractal. A partir deste trabalho de Mandelbrot, questões relativas à similitude entre uma figura e a sua ampliação começaram a aparecer, cada vez com maior freqüência, na literatura científica.

Tecnicamente, um fractal é um objeto que apresenta invariância na sua forma à medida em que a escala, sob a qual o mesmo é analisado, é alterada, mantendo-se a sua estrutura idêntica à original. Isto não é o que ocorre, por exemplo, com uma circunferência, que parece reduzir a sua curvatura à medida em que ampliamos uma das suas partes.

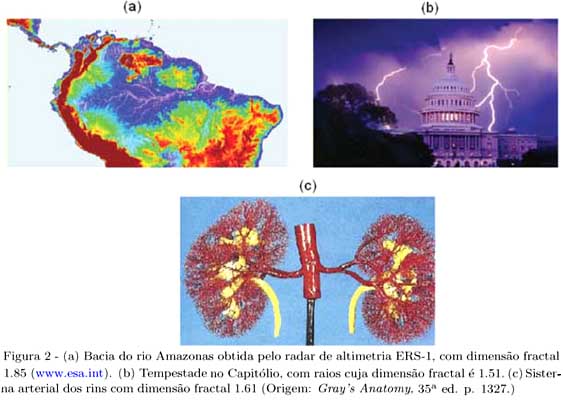
As principais propriedades que caracterizam os fractais são a auto-semelhança, a complexidade infinita e a sua dimensão. A auto-semelhança é identificada quando uma porção, de uma figura ou de um contorno, pode ser vista como uma réplica do todo, numa escala menor. Esta característica pode ser melhor entendida a partir do exame da Fig. 1. A complexidade infinita refere-se ao fato de que o processo de geração de uma figura, definida como sendo um fractal, é recursivo. Isto significa que, quando se executa um determinado procedimento, no decorrer da mesma encontra-se como sub-procedimento o próprio procedimento anteriormente executado. Vale salientar que, no caso da construção iterativa de um fractal matematicamente definido, dispõe-se de um número infinito de procedimentos a serem executados, gerando-se assim uma estrutura infinitamente complexa (ver Fig. 1). Finalmente, a dimensão de um fractal, ao contrário do que ocorre na Geometria Euclidiana, não é necessariamente um valor inteiro. Nela, um ponto possui dimensão zero, uma linha possui dimensão um, uma superfície possui dimensão dois e um volume possui dimensão três. No caso da dimensão fractal, ela é uma quantidade fracionária, representando o grau de ocupação da estrutura no espaço que a contém. Como exemplos, pode-se citar a dimensão fractal da bacia fluvial do rio Amazonas que é 1.85 [2], dos relâmpagos no espaço tridimensional, 1.51 [3], dos angiogramas dos rins, 1.61 [4], dentre outros (ver Fig. 2).

O conceito de dimensão fractal vem atualmente sendo aplicado e calculado para linhas, figuras ou superfícies em diversos campos. Na medicina, por exemplo, como método de diagnóstico quantitativo de patologias. Um dos campos onde este procedimento \'e mais desenvolvido é o diagnóstico do câncer, através da análise de imagens de tumores. As evidências experimentais sugerem que tumores de câncer apresentam uma fronteira com dimensão fractal superior às que ocorrem em agregados de tecidos normais. Um exemplo, nesta linha de investigação, é o da detecção de núcleos atípicos [5] (ver Fig. 3 (a)). Na tecnologia de fabricação de antenas, o conceito de dimensão fractal também ganha importância. A resposta das antenas fractais difere acentuadamente das tradicionais, uma vez que são capazes de funcionar de forma otimizada, simultaneamente em várias freqüências. Esta característica faz das antenas fractais uma excelente alternativa para aplicações de recepção de banda larga (ver Fig. 3 (b)). Pode-se também verificar aplicações nas mais diversas áreas da ciência, listando-se aplicações na Minerologia [6], com o objetivo de medir a densidade dos minerais, a evolução dos terrenos e a descontinuidade das rochas; na Biologia para a análise da rugosidade dos fungos [7] e de corais [8]; na indústria com a detecção automática de falhas em produtos têxteis [9]; no solo [10], na chuva [11], na economia [12], na ecologia [13].

O objetivo deste trabalho é apresentar, de maneira rigorosa, o cálculo da dimensão fractal de conjuntos definidos por leis de construção recorrentes, que levam a figuras auto-similares em todas as escalas. Este procedimento, conquanto não possa ser usado para a análise de objetos reais, é relevante por servir de base para a introdução e determinação quantitativa da geometria fractal.

2. Alguns aspectos a respeito da geometria fractal

O termo fractal aplica-se, em geral, a construções diversas, tanto nas ditas formas abstratas como nas formas inerentes à natureza, que são objeto de estudo da Física, enquanto forma e leis de formação e de escala. A discussão a respeito da geometria fractal requer uma análise sobre os tipos de fractais que existem, bem como das características matemáticas que os definem, como comprimentos, áreas e as correspondentes dimensões fractais.

Uma característica associada aos fractais gerados por sistemas de funções iterativas é a auto-similaridade exata, ou seja, a variação do comprimento de escala, sob a qual o fractal é analisado, o que leva sucessivamente a configurações idênticas à configuração inicial. Existem, contudo, fractais que são igualmente formados por minicópias, mas estas são anisotrópicas, ou seja, não são mantidas fixas às proporções originais em todas as direções. Ao se passar de uma escala para outra, observa-se que o tamanho destas cópias não varia uniformemente em todas as direções do espaço. Neste caso, os fractais são chamados de auto-afins. Como exemplo destes fractais aproximados, encontrados na natureza, tem-se as células tumorais pertencentes à evolução do câncer. Estudos feitos nesta área afirmam, que na transição de um tumor benigno para um maligno, a interface tumor/tecido sadio torna-se irregular com uma estatística que caracteriza a auto-afinidade [5] (ver Fig. 3(a)). Outros exemplos de configurações auto-afins podem ser verificados no estudo de séries temporais rugosas [14], precipitações [11], atividades financeiras [12], entre outras áreas de investigação.

2.1. Fractais determinísticos ou auto-similares

Neste texto abordaremos as estruturas com geometria fractal que, por apresentarem uma auto-similaridade exata, são denominadas de fractais determinísticos. Por auto-similaridade exata entende-se a invariância da estrutura após uma transformação isotrópica, i.e., que se dá com a mesma intensidade em todas as direções. Se tomarmos um objeto S, constituído por um conjunto de pontos R = {x₁,x₂,x₃,...}, a aplicação de uma tranformação auto-similar com um fator de escala b, muda as coordenadas dos pontos para bR = {bx₁,bx₂,bx₃,...}. Logo, o conjunto S, formado pelos pontos de coordenadas R, é auto-similar se este resulta invariante após a referida transformação. Para exemplificar, considere-se um fractal denominado de triângulo de Sierpinski, como mostrado na Fig. 4 (a). Sua construção básica começa com um triângulo equilátero, totalmente preenchido. Inicialmente toma-se os pontos médios dos três lados que, juntamente com os vértices do triângulo original, formam quatro triângulos congruentes. Em seguida, retira-se o triângulo central, concluindo-se assim a primeira etapa do processo básico de construção. Esta retirada resulta em três triângulos congruentes, cujos lados medem metade do lado do triângulo original. Repete-se, com cada um destes três triângulos, o procedimento anteriormente descrito. Com os triângulos resultantes repete-se o mesmo procedimento. Desta maneira, começando-se com um único triângulo, geram-se, seqüencialmente, 3, 9, 27, 81, ... triângulos, correspondentes aos níveis 1, 2, 3 e 4 respectivamente, representados na Fig. 4 (b). Esta mesma lei de formação é sucessivamente aplicada, de modo que sua estrutura com forma triangular é constituída por triângulos seqüencialmente menores que são cópias perfeitas da forma inicial da figura. Assim, ao ampliar-se ("zoom") uma parte qualquer, ter-se-á algo idêntico à figura como um todo (ver Fig. 4 (a)). No limite de infinitas aplicações deste procedimento obtém-se uma figura fractal auto-similar exata, ou simplesmente denominada de auto-similar.

2.2. A Dimensão Fractal

A dimensão euclidiana, é um conceito clássico, restando porém considerar importante ou pelo menos conveniente repeti-lo aqui. Tal dimensão, representa o número de coordenadas necessárias para descrever uma forma euclidiana. Por exemplo, uma coordenada (chamada comprimento) descreve uma linha. Duas coordenadas (comprimento e largura) são necessárias para descrever um plano e três coordenadas (comprimento, altura e largura) descrevem um volume. É simples então perceber, que desse ponto de vista um ponto tem dimensão zero. Usualmente, a dimensão euclidiana está associada a eixos perpendiculares, especificando portanto em uma, duas ou três dimensões algum ponto pertencente a uma linha, área ou volume respectivamente. Por indução, pode-se ampliar o raciocínio, sucessivamente, até n dimensões, ainda que reste sensorialmente impossível perceber além da terceira dimensão. Vale salientar que as dimensões associadas à geometria euclidiana são sempre números inteiros.

Considere-se, por exemplo, a curva de Koch, conforme mostrada na Fig. 5. A construção se dá a partir de um segmento de reta que, em seguida, é dividido em três segmentos iguais. Depois disto, substitui-se o terço médio por um triângulo equilátero retirando-lhe a base. O processo iterativo consiste em aplicar a mesma regra a cada um dos segmentos de reta que resultam da iteração imediatamente anterior. Considerando-se cada passo nota-se que, de um nível para a seguinte, substituem-se três segmentos por quatro de igual comprimento, ou seja, o comprimento total é multiplicado por 4/3 correlacionando-se níveis sucessivos. O limite de uma sucessão geométrica de razão 4/3 é infinito, o que significa que a figura final, i.e., aquela para a qual tende a sucessão descrita, terá um comprimento infinito. Este limite foi denominado por Mandelbrot como "infinito interno". Portanto, no n-ésimo nível, o comprimento da curva de Koch será dado por

Assim, no limite de um número infinito de níveis, tem-se o seguinte resultado

Uma curva deste tipo, devido à sua complexidade infinita, contém um número de infinitas "dobras" que, se ampliadas, continuam aparecendo indefinidamente. Devido a este infinito detalhamento, esta curva "ocupa mais espaço" que uma linha convencional, possuindo assim uma dimensão fractal maior que 1.0, sem chegar, no entanto, a ocupar o espaço de uma faixa que a contém (dimensão 2.0). Desta maneira, conceito de dimensão fractal, D, está intimamente relacionado com a estrutura de ocupação do espaço da figura. Para tal se fazem necessárias duas definições anteriores de dimensão: a dimensão topológica e a dimensão de imersão. A dimensão topológica D_t pode ser definida iterativamente a partir da definição da dimensão topológica de um ponto como sendo zero. A dimensão topológica de outros objetos é dada pelo valor de D_t do elemento que o torna desconexo [15] mais 1. Para uma curva, um ponto é suficiente para torná-la desconexa de forma que o correspondente valor de D_t será 0+1 = 1. Para o plano, uma curva o torna desconexo, o que leva a 1+1 = 2 e para um volume, uma vez que uma superfície o torna desconexo, 2+1 = 3. Vale observar que os valores numéricos das dimensões topológica e euclidiana, são usualmente coincidentes, apesar de serem dimensões distintas no que diz respeito à maneira pela qual são definidas. A dimensão de imersão, D_i, como sugere o nome, representa a dimensão na qual o objeto está imerso. Como ilustração, pode-se usar como exemplo as letras deste texto. Estas têm dimensão topológica 1, contudo estão imersas no espaço da folha do papel, ou tela do computador, o que implica em que sua dimensão de imersão seja 2.

A dimensão fractal, D, ou de medida, tem como conceito básico a noção intuitiva de preenchimento do espaço. Em razão disto, existe a necessidade de se estabelecer uma definição do que é um fractal e que atenda a todas as espécies de construção. Para Mandelbrot [1], "Um dado conjunto A constitui um fractal se, em A, D_i > D > D_t, sendo D a dimensão fractal e D_t a dimensão topológica do conjunto A". Kenneth Falconer [15] propõe uma definição menos rigorosa em termos das características dos fractais. Uma destas características seria a complexidade infinita, ou seja, o fato que sucessivas ampliações de um fractal levam, indefinidamente, a mais detalhes como já discutido.

A dimensão fractal de um conjunto, parte-se da definição de espaço métrico Rⁿ. Na reta definimos um intervalo como um segmento de reta, enquanto que no Rⁿ o intervalo é definido como uma esfera de raio e, centrada em x_i. Esta esfera será representada por B(x_i,ε), sendo então uma bola aberta definida como B(x_i,ε) = {y_i Є Rⁿ/d(x_i, y_i) < ε}, onde d(x_i, y_i) é a métrica do espaço Rⁿ que pode ser expressa por

onde x_i = (x₁, x₂,...,x_n) e y_i = (y₁,y₂,...,y_n), e satisfaz os seguintes axiomas

(i) d(x_i, y_i) > 0 ∀ x_i, y_iЄ Rⁿ, e d(x_i, y_i) = 0 ⇔ x_i = y_i

(ii) d(x_i, y_i) = d(y_i, x_i) ∀ x_i, y_i Є Rⁿ

(iii) d(x_i, z_i) < d(x_i, y_i) + d(y_i, z_i) ∀ x_i, y_i, z_i Є Rⁿ

Já uma bola fechada é definida como: B(x_i,ε) = {y_i Є Rⁿ/d(x_i, y_i) < ε}. Representa-se o menor número de bolas fechadas de raio e necessário para se ter uma cobertura A, com A ⊂ Rⁿ e ε > 0, por N(A,ε).

Um conjunto A, terá características fractais se [16]

sendo C uma constante positiva.

Daí segue-se que

Calculando-se o logaritmo neperiano dos dois membros da relação 5, tem-se

e, portanto

Como ln(C)/ln() tende a 0 à medida em que ε → 0, segue-se que a dimensão fractal de um conjunto pode ser definida pela seguinte expressão

2.3. Propriedades de alguns fractais auto-similares

Entre a segunda metade do século XIX e a primeira metade do século XX, foram propostos vários objetos matemáticos com características especiais que foram, durante muito tempo, considerados como "monstros matemáticos", uma vez que desafiavam as noções comuns de infinito e para os quais não havia uma explicação objetiva. Uma vez que os fractais exibem, como propriedade, a infinita complexidade, as medidas clássicas de comprimento, área ou de volume perdem o sentido intuitivo. Descrevemos neste trabalho algumas propriedades clássicas associadas a alguns fractais auto-similares que confirmam tal hipótese.

2.3.1. Conjunto de Cantor

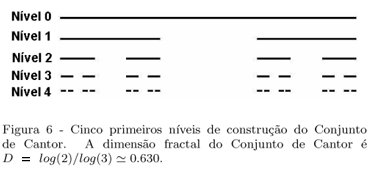
Cantor (1845-1918), que se destacou por apresentar idéias altamente inovadoras sobre o conceito de infinito, propôs a construção de um objeto que resultou chamar-se de conjunto de Cantor [18]. A construçcão geométrica do conjunto de Cantor recebe, por vezes, o nome de "Poeira de Cantor". Para sua construção, inicia-se com um segmento de reta de comprimento unitário. Divide-se este segmento em 3 partes iguais, retirando-se o seu terço médio. Essa é a primeira etapa, ou primeiro nível, da construção. Na segunda etapa, retira-se o terço médio de cada um dos dois segmentos restantes da primeira etapa. As porções restantes são novamente divididas e delas são retirados os terços médios, procedendo-se sucessivamente do mesmo modo. O processo é repetido fazendo-se o número de etapas, ou níveis, N, tender a um número infinitamente grande. A figura obtida quando N → ∞ é o conjunto de Cantor. Algumas etapas da sua construção são mostradas na Fig. 6.

É interessante analisar o que acontece com o número de segmentos, n_N, com o comprimento de cada segmento, c_N, bem como com o comprimento total do conjunto, C_tN, em cada geração N de sua construção. Entende-se por comprimento total a soma dos comprimentos dos segmentos de um conjunto. No nível inicial, ou seja, para N = 0, tem-se um segmento de modo que n₀ = 1. No nível 1, têm-se 2 segmentos. No nível 2 são quatro segmentos, enquanto na geração 3 são oito segmentos. Deste modo, decorre imediatamente desta construção, que no n-ésimo nível, o número de segmentos é 2^N, ou seja

No Conjunto de Cantor, isto é, para N → ∞, tem-se

ou seja, nesta estrutura, o número de segmentos tende ao infinito.

Uma característica, aparentemente paradoxal com a afirmação anterior, pode ser verificada ao se analisar o comprimento total do conjunto de Cantor, C_tN. Para isso, é necessário primeiramente analisar o comprimento de cada segmento, c_N, que compõe o Conjunto de Cantor no correspondente nível. No primeiro nível, N = 0, o comprimento do segmento é c_N=1; no segundo nível c_N = 1/3; no terceiro nível c_N = 1/9. Então, no n-ésimo nível, o comprimento de cada segmento é expresso por

Portanto tem-se que, no limite para infinitos níveis

Desta maneira, o comprimento de cada segmento tende a zero. Por isso, o resultado do conjunto de Cantor é uma série de pontos "pulverizados"; daí a denominação de "Poeira de Cantor".

Para se analisar o comprimento total C_tN do conjunto de Cantor, basta que se multiplique o número de segmentos pelo comprimento de cada um deles. Logo

Quando o número de gerações tende a infinito, tem-se

Portanto, o comprimento do Conjunto de Cantor tende a 0. Observam-se pois características do conjunto de Cantor que são paradoxais. Ao mesmo tempo em que o número de segmentos de que é composto o conjunto tende a infinito, conclui-se que o conjunto de segmentos possui um comprimento total nulo. As construções matemáticas que encerram tais contradições são comumente chamadas de "Monstros Matemáticos" ou ainda de "Casos Patológicos".

É natural então que se conclua que o Conjunto de Cantor possui uma dimensão que se situe entre 0 e 1. Com efeito, para este resultado basta considerar o conjunto de bolas unidimensionais como sendo formado, em cada nível, por segmentos de reta de comprimento = (1/3)^N e que para cobrir a estrutura, necessita-se de N (A, ) = 2^N segmentos. É claro que → 0 quando N → ∞. Assim, para esta configuração auto-similar, utilizando-se a expressão 7, tem-se D = log(2)/log(3) = 0.630...

2.3.2. Ilha de Koch

Nesta seção é discutido um dos processos de formação do que se denomina de Ilha de Koch. No caso, parte-se de uma linha fechada, denotada de "ilha", que tem como geração inicial a forma de um triângulo equilátero. O processo de construção se inicia substituindo o terço central de cada um dos lados, supostos cada um de comprimento unitário, por outros dois segmentos com comprimentos de 1/3, formando-se uma estrutura triangular, sem a base que justamente corresponderia à porção removida, como já explicado na seção 2.2. Obtem-se então uma estrutura com comprimento total de 4 unidades (três conjuntos de quatro partes cada um, cada parte com comprimento 1/3). O processo é repetido para cada um dos doze segmentos, sucessivamente, até que para infinitos níveis tem-se a estrutura chamada de Ilha de Koch (ver Fig. 7).

Primeiramente procede-se a uma análise de como a área, limitada pelos segmentos que constituem a figura, muda no processo iterativo. No nível inicial, N = 0, tem-se um triângulo equilátero de lado l, cuja área S₀ é dada por

Para o segundo nível, ou seja, para N = 1, acrescenta-se à área do triângulo original, 3 triângulos de lado l/3. Assim, a área S₁ da ilha será

Para o terceiro nível, ou seja, para N = 2, acrescenta-se à área da estrutura resultante para N = 1, 12 triângulos de lado l/9. Assim, a área S₂ será dada por

Logo, para o n-ésimo nível, tem-se

A Eq. (18) pode ser reescrita como

Fazendo N → ∞, tem-se que o somatório da Eq. (19) é uma série geométrica de razão q = 4/9, de modo que tem-se

Portanto, tomando-se o limite da área S_N para infinitos níveis, tem-se

A expressão para o perímetro da Ilha de Koch pode ser facilmente determinada, a partir da análise feita na seção 2.2. Como cada lado do triângulo equilátero (N = 0), corresponde a um segmento gerador da Curva de Koch, então o perímetro da construção da Ilha de Koch para o n-ésimo nível, T_N, é dado por

Estes resultados mostram que a área, delimitada por uma linha de comprimento infinito, de acordo com o processo de construção exposto nesta seção, é finita. A dimensão fractal da ilha de Koch é determinada de modo que, para o nível N, o número de segmentos de comprimento (1/3)^N que recobrem a correspondente curva, é dado por 4^N. Portanto, obtém-se, a partir da expressão 7, o valor D = log(4)/log(3) = 1.26...

2.3.3. Gaxeta de Sierpinski

Nesta seção será discutido o processo de construção da Gaxeta de Sierpinski, também conhecida como Triângulo de Sierpinski. São apresentadas algumas características geométricas do mesmo, como o cálculo da área obtida para diferentes níveis e o cálculo do comprimento resultante para infinitos níveis no processo de construção. Um processo simples de construção do Triângulo de Sierpinski se inicia a partir de um triângulo equilátero totalmente preenchido (nível inicial, N = 0). Posteriormente determinam-se os pontos médios de cada um dos três segmentos que delimitam o triângulo inicial, de modo que, ligando-se estes três pontos médios, obtém-se quatro triângulos onde cada lado corresponde à metade do lado do triângulo inicial. Ao retirar-se o triângulo central tem-se a segunda configuração correspondente a N = 1, concluindo-se portanto o processo básico de construção. O processo é repetido com cada um dos três triângulos restantes (Ver Fig. 4(b)), e sucessivamente com cada triângulo equilátero formado na seqüência.

Para a determinação da área do Triângulo de Sierpinski, considera-se inicialmente um triângulo equilátero de lado l, cuja área, S₀, é dada por

Em cada passo N, subtrai-se a área de n_N triângulos com lados l_N. Tem-se então que n₁ = 1, n₂ = 3, n₃ = 9, ..., n_N = 3^N-1. Os lados l_N, são obtidos pela redução dos lados do triângulo original por um fator 1/2, ou seja

Desse modo, a área S₁ será expressa por

A área S₂ será dada por

Para N = 3, ter-se-á

Multiplicando e dividindo o segundo membro da Eq. (27) por 3, a mesma pode ser simplificada à seguinte forma

Portanto, para N → ∞ obtém-se

É interessante discutir o perímetro de cada um dos triângulos obtidos em cada nível da construção para se calcular a soma do perímetro dos 3^N triângulos no nível N. Esta análise permite calcular a soma dos perímetros dos triângulos da figura como um todo. Analogamente ao que foi feito para determinação do número de triângulos, n_N, determina-se o perímetro de cada triângulo para um determinado nível. Para N = 0, tem-se o perímetro do triângulo original de lado l, ou seja, T₀ = 3l. Para N = 1, o lado de cada triângulo gerado será l/2, o que resulta em um perímetro 3l/2. Para N = 2 o lado de cada triângulo gerado será l/4, o que resulta em um perímetro 3l/4, para cada triângulo. Portanto, para o nível N, tem-se que o perímetro de cada triângulo, T_N, resulta em

Como o número adicional de triângulos removidos do nível N é 3^N, a soma P_N dos perímetros dos triângulos no nível N é dada por

Para o Triângulo de Sierpinski, quando N → ∞, tem-se

Logo, o perímetro aumenta indefinidamente à medida que aumentamos o número de níveis na construção do Triângulo de Sierpinski. Isto leva a uma conclusão aparentemente paradoxal: a área total de todos os triângulos tende para zero enquanto que o perímetro da estrutura formada, aumenta indefinidamente. A dimensão fractal deste fractal pode ser determinada se notarmos que tal estrutura é formada por três cópias de si mesma, cada uma reduzida por um fator de 1/2. Assim, a partir da expressão 7, substituindo as bolas de raio por triângulos equiláteros de lado l/2^N, chega-se portanto à expressão D = log(3)/log(2) = 1.58... Este resultado indica, portanto, que a gaxeta de Sierpinski só pode ser adequadamente medida em um espaço cuja dimensão é determinada pela sua dimensão fractal D_f.

2.3.4. Esponja de Menger

A construção da Esponja de Menger é baseada no mesmo princípio utilizado para a construção do Triângulo de Sierpinski. Contudo, o processo iterativo é feito com um cubo, estendendo-se portanto a uma situação tri-dimensional (ver Fig. 8).

O processo de construção se dá de tal forma que, para N = 0, tem-se um cubo maciço de lado l e com volume V₀ = l³. Para N = 1, o cubo é dividido em 27 cubos menores e iguais, cada um com uma aresta igual a l/3. Remove-se o cubo central, bem como os seis cubos situados no meio de cada face do cubo maior. Este processo é repetido seqüencialmente com todos os cubos restantes, dividindo cada um em 27 outros com 1/3 da aresta do cubo imediatamente anterior. Similarmente, remove-se o cubo central e cada cubo na porção central das faces. No segundo nível, ou seja, N = 1, o volume da esponja, V₁, será dado por

No terceiro nível, ou seja, N = 2, cada um dos 20 cubos restantes são divididos em mais 27 cubos iguais, dos quais 7 são retirados, cada um com volume (l/9)³. Deste modo, o volume da esponja, V₂, será dado pela expressão

A Eq. (34) pode simplesmente ser reescrita na forma

Portanto, para o n-ésimo nível, fazendo N → ∞, o volume da esponja será dado por

Logo, observa-se que o volume da Esponja de Menger tende a zero, quando o número de níveis tende a infinito. Para determinação da área da superfície desta estrutura fractal, S_N, tem-se que para N = 0, S₀ = 6l². Para N = 1 tem-se

Portanto, para o n-ésimo nível, com N → ∞, a área da superfície associada à esponja será dada por

Conclui-se então, que a Esponja de Menger possui volume nulo e uma área infinita na medida em que o número de níveis tende a infinito. Neste caso o cálculo da dimensão fractal, pelo mesmo método usado anteriormente, leva a D = (log 20)/(log 3) = 2,726...

3. Considerações finais

O objetivo deste trabalho foi trazer ao leitor casos simples, mas ilustrativos, que mostram como diversos objetos auto-similares só podem ser adequadamente medidos em espaços de dimensão fracionada. Através do cálculo de comprimento, área e volume, para tais objetos, fica explicitado que estas medidas podem divergir ou se anular identicamente quando a sua dimensão é respectivamente maior ou menor do que aquela dimensão Euclidiana escolhida pra se efetuar a medida. Conquanto o conceito de dimensão fractal seja apresentado em diversos textos, cremos que o cálculo explícito de medidas de objetos fractais em espaços de dimesão inteira facilitará ao leitor a apreensão do conceito de medidas de dimensão fracionada.

4. Agradecimentos

O trabalho de pesquisa que os autores desenvolvem nas suas respectivas instituições tem o apoio da FAPESB, CNPq e AECI.

Referências

[1] B.B. Mandelbrot, The Fractal Geometry of Nature (W.H. Freeman and Company, Nova Iorque, 1975).

[2] H. Takayasu, Fractals in the Physical Sciences (Manchester Univ. Press, Manchester, 1990).

[3] J. Sanudo, J.B. Gomez, F. Castano, A.F. Pacheco, Nonlinear Processes in Geophysics 2, 101 (1995).

[4] S.S. Cross, R.D. Start, P.B. Silcocks, A.D. Bull, D.W. Cotton and J.C Underwood, J. Pathol. 170, 479 (1993).

[5] R. Sedivy, M.D. Windischberger, M.K. Svozil, E. Moser and G. Breitenecker, Gynecologic Oncology 75, 78 (1995).

[6] Z. Zheru, M. Huahai and Q. Cheng, Math. Geol. 33, 33 (2001).

[7] L.C. Jones and G.T. Lonergan, Biotech. Lett. 19, 65 (2004).

[8] H. Bradbury and E. Reichelt, Mar. Ecol. Prog. Ser. 10, 169 (1983).

[9] C.B. Proença, A. Conci and S.A. Segenreich, J. Braz. Soc. Mech. Sci. 21, 493 (1999).

[10] S.W. Tyler and S.W. Wheatcraft, Soil Sci. Soc. Amer. 25, 109 (1990).

[11] J.G.V. Miranda and R.F.S. Andrade, Physica A 295, 38 (2001).

[12] P.C. Muñoz, M.F. da Silva, J.G.V. Miranda, F. Claro and R. G. Diniz, Physica A (in press).

[13] G. Sugihara, B. Grenfell and R.M. May, Phil. Trans. R. Soc. London B, 330, 235 (1990).

[14] J.G.V. Miranda and R.F.S. Andrade, Theor. Appl. Climatol. 63, 79 (1999).

[15] K. Falconer, Fractal Geometry - Mathematical Foundation and Applications (John Wiley & Sons, Chichester, 1990).

[16] A.L. Barabási and H.E. Stanley, Fractal Concepts in Surface Growth (Cambridge University Press, Cambridge, 1995).

[17] R.R. Goldberg, Methods of Real Analysis (Blaisdell, Nova Iorque, 1963).

[18] J.W. Dauben, Georg Cantor: His Mathematics and Philosophy of the Infinite (Cambridge, Massachusetts , 1979).

Recebido em 27/9/2007; Revisado em 27/12/2007; Aceito em 31/1/2008; Publicado em 21/7/2008

2

No Português arcaico,

franger significa fazer em pedacos; quebrar, destrocar, frangir.

Datas de Publicação

• Publicação nesta coleção
  20 Ago 2008
• Data do Fascículo
  2008

Histórico

• Revisado
  27 Dez 2007
• Recebido
  27 Set 2007
• Aceito
  31 Jan 2008