Conservation laws for non-potential operators

Conservation Laws for Non-Potential Operators

Vera Lia Marcondes Criscuolo de Almeida

Universidade Estadual Paulista, UNESP

Departamento de Matemática C.P. 205

12500-000 Guaratinguetá, SP Brazil

Email: [e-mail]

Antonio Marmo de Oliveira

Universidade de Taubaté, UNITAU

Departamento de Engenharia Civil

12010-170 Taubaté, SP Brazil

Abstract

The aim of this work is to study the conservation laws of continuous means mechanics and also to extend the Hamiltonian method for these kind of systems in order to valid for non-potential operators through variational approach. Besides illustrating with various examples of mechanical applications we also introduce in this work the new technique in order to treat such problems as the non-potential problem.

Keywords: Conservation Laws, Non-Potential Operators, Hamilton's Method.

Introduction

Nowadays the variational principles are used mainly in the following contexts:

i) obtaining the differential equations for a physical problem with its corresponding boundary conditions;

ii) the study of the symmetry and conservation laws under infinitesimal transformation groups;

iii) it proves that a given boundary problem has solution (that is, demonstration of the existence solution for non-linear equations);

iv) obtaining solutions of linear and non-linear problems using direct methods of variational calculus

The use of variational principles in cases (iii) and (iv) leads to the so-called "inverse problem of the calculation of variations", that is, the existence and formulation of a functional one, in which the variation, once disappeared, supplies the boundary problem in consideration.

Historically the inverse problem of the calculation of variations is related to the idea of finding a potential for a non-conservative force.

The first work in this context, due to Lagrange, 1773, defines as conservative any force (F) that derives of a potential (V), which is function only of the position:

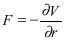
Even so, not all the forces are potential in the Lagrangean sense.

The first attempt to enlarge this notion was made by Weber [13]. He tried to generalize the idea of a potential (V), supposing that it depends could not only on the position, but also on the velocity of the particles.

In this case the force is defined for

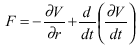
The condition for F be derivable from a potential is that the following symmetry condition between the force F and the vectorial position r is valid:

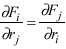
For the potential forces proposed by Weber [13], the symmetry conditions were deduced by Helmholtz, 1886.

As one can observe, Weber's definition [13] is equivalent to declare that F must be the same to variational derivative of a potential scalar function (V), when it depends only on the position and velocity.

The generalization of those ideas came from the definition of a potential operator as an operator is acting of a space of Hilbert for its dual one, that it can be obtained of a gradient of a functional one for all the elements of its domain.

The symmetry conditions and potentiability for operators, first enunciated by Kerner, 1933 and they were demonstrated by Vainberg, 1973, relating the symmetry of an operator to an equality of its second-order Gateaux derivatives.

Definition 1:

Let U be a vectorial space, U' its dual one, N : U®U' an operator non-linear Gateaux differentiable. The operator N is non-potential if

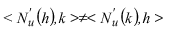
where < .,. > represents duality between appropriate spaces U and U' (Sobolev's spaces, for example).

In the following it is associated to all equation of evolution of the type shown above

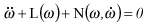
(where L is the symmetrical linear operator and N is a non-symmetrical operator) a function M invariant in the time. Initially a study on how to build such function M is presented by means of a Hamiltonian function H, with the purpose of obtaining Conservation Laws for Non-conservative problems. As H is associated to the energy of the conservative systems, it is by analogy that M is a meta-energy of the system. When the considered system was conservative M should coincide with H.

The demonstration that M is invariant, associated the evolution equation , is seen in the theorem 1.

Some typical problems of the literature are selected to illustrate the concept presented in the theorem 1. The first one is denominated

Beck's Problem, which represents a classic example of a loaded elastic system non-conservatively; the second one is the case of the Leipholz's bar and finally, the third one is the application of the meta-energy M for a cantilever Euler-Bernoulli beam, endowed with visco-elastic material of the Kelvin's type, subjects to a compressive force P in its free extremity.

Meta-energy for the Case of Non-Potential Operators

The class of operators considered in this work is the differentiable operators for differentiable Gateaux, these operators and acting in Sobolev's spaces chosen for the approached problems.

Theorem 1: Almeida, 1993,

Let it be w = w(x, t) a function, L a symmetrical linear operator, N a non-symmetrical operator and the function Hamiltonian H given for

(1)

where

If

(2)

it describes the equation of the motion (evolution equation), then

(3)

is an invariant, of that movement, that is

.

Test:

From the definition of M it can be obtained that

(4)

However,

and

(5)

therefore,

(6)

From equation (6) one can demonstrate that M is an invariant in the time.

Reciprocally, if

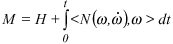
With

, then

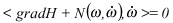
and

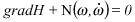
is the equation of motion of the system.

It is observed that the applicability of the Theorem 1 to physical models depends only on the differenciability restrictions and on non-symmetry of the involved N operators.

In the following sections three restricted examples of the theory are given of the beams analysing in small deformations. These restrictions can be eliminated substituting the linear operator symmetrical L for a non-linear symmetrical operator F = grad H. This implies a small modification in the hypotheses of the Theorem 1 and it will not be done due to space limitation.

Depending on the nature of the non-linear, non-symmetrical operator N, the studied physical model can be here more complex than the examples presented in this work, it's involving, for example, the processes non-isotermics.

The first two examples are about elastic beams which are submitted to followers loads (Beck and Leipholz's problem); they are interesting because of the break symmetry the boundary conditions (In the physical point of view it can be noticed), due to the fact of the follower load work depends on the trajectory.

The third example is about a beam with simple visco-elastic behavior, where the loss of the symmetry happens due to the existence of a dissipation associated to the nature of the material.

On the other hand, in the Theorem 1, it is demanded that N is not symmetrical. That hypothesis is fundamental, because if N is symmetrical the problem will be conservative and consequently suject of the classic Hamiltonian analysis.

Example 1: The Beck's problem, Leipholz, 1977, Oliveira et al., 1982, Terni, 1990

The motion of Beck's column is described by the following equation which the boundary conditions given by equation (8):

(7)

(8)

where w( x, t ) indicates the lateral deflection of the beam; EI is the rigidity to the flexion; P is the tangential load ,compressive and independent of the time; is the length of the bar and m denotes the mass density for unit of length.

In the sense of the mechanics, the adjoint system for the Beck's column can be interpreted as the Reut's column shown in the illustration 2

In the literature regarding the bar of Beck, Leipholz, 1977, it is generally considered the following approaches: Pv PeP_H = Pj, where j (, t ) it is the angle between the load P and the axis x. The moment in the clamped extremity of the bar is given by M(0,t) = El(0,t) and the shear effort by Q(0,t) = – El(0,t).

Corresponding to all those efforts there is an energy H and two meta energy M and M_cont. The function hamiltonian H is the sum of the kinetic energies, of flexion and compression

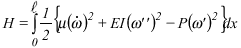
It is noticed that to the horizontal component P_H of the load P varies with the trajectory, consequently the operator N will correspond to the Non-conservative load, that is, N = P(l,t) = P_H[7] , and as before , increased of the portion M_cont, that is exactly the work of the internal efforts due to the contour conditions in the point x = 0, that is to say,

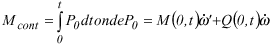
Therefore, it is conclude D that

(9)

where

(10)

It is shown that M is an invariant in the time, because,

(11)

by observing the equations (7) and (8). Reciprocally M = 0 implies the equation of the motion (7) and the conditions contour (8).

Example 2: The Leipholz's bar ,Leipholz, 1977

It is considered the problem of Leipholz's bar presented as the following boundary problem

(12)

(13)

where w (x, t) indicates the lateral deflection; EI is the rigidity to the flexion and m denotes the mass density for unit of lenght .

This problem describes the case of a set column in its inferior extremity, free in the superior extremity, with a load follower g tangencial to the deformed axis of such column, according to illustration 3.

Examining the expressions (12) and (13), it is identified the following operators:

(14)

and

(15)

so that the equation of the problem results in:

(16)

Defining

(17)

the expression invariant in the time, can be obtained as

(18)

where

(19)

It appears due to the entail, once the moment in the setting of the bar is given by M(0,t) = EI

(0,t) and the sharp effort by Q(0,t) = – EI

(0,t)

In fact, if , it is obtained:

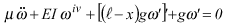
that is the equation of the motion of Leipholz' bar. The several terms presented in the expression (18) can be interpreted in the following way:

• the term is the potency due to there horizontal component of the force g, while the term , present in , is the potency of the internal efforts due to the contour conditions in the point x = 0.

However M – M _cont is the sum of two integrals, the density of mechanical energy H and the density of energy G of the force follower horizontal component g, that is to say,

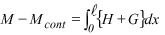
where

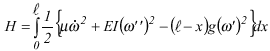
and

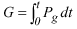
In the following example, it is illustrated how to obtain the equation of the motion derived the meta-energy M.

Example 3: Beam with viscous reduction

Let be considered a beam of Euler-Bernoulli (in swinging) whose material is visco-elastic of the type length Kelvin , subject to a compresive force P in its free extremity see:

Fig. 5 Beam with viscous reduction

Suppose that the material of the bar obeys the following relationship of Kelvin 's type,Gurtin et al., 1962.

(20)

where s is the normal tension, E the elasticity module, E' the viscous reduction module and e the normal deformation.

If w represents the deflexible beam, then it can be energies kinetics

(21)

stored potential,

(22)

and the dissipated energy,

(23)

where m is the density of mass.

The energy M will be given by M=T+V+D+M _contorno, that is to say,

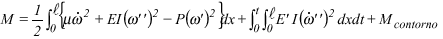
with

(25)

The term M _contorno was built by analogy with the contour terms that appear in the formulation classic Hamiltonian, however there is a difference on its physical meaning. Examining the expression (25) it can be noticed that M _contorno is a work in the resulting contour of the integration in the time of potencies (instead of work). For example, the terms it is the potency due to the sharp effort in the setting x = 0. The other terms have similar interpretation.

The expression M = 0 will supply the motion equation and the contour conditions, as it proceeds:

(26)

Making integration by parts, one arrives to

(27)

And it can be concluded that M = 0, if and only if

(28)

(29)

Conclusion

A study was developed in this work in order to build a function M invariant in time, by means of Hamiltonian's formulation, taking into account the equation of evolution associated to the problem, showing that starting from this function the equation of the motion of the system with the contour conditions for Non-conservative considered problems can be obtained.

Manuscript received: March 1997, Technical Editor: Leonardo Goldstein Jr.

• Almeida, V.L.M.C., 1993, "Leis de Conservação na Mecânica do Contínuo". ITA, Tese de Doutorado
• Gurtin, M.E. and Sternberg, E., 1962, "On the Linear Theory of Viscoelasticity", vol. 11. Arch. Rational Mech. Anal, Berlim.
• Helmholtz, J., 1886, Math.c..
• Lagrange, J.L., 1773, Oeuvres VI, 355.
• Kerner, M., 1933, "Die differentiale in der algemeinen analysis". Ann. Math. 34 (2), 546-572.
• Leipholz, H., 1974, "On Conservative Elastic Systems of the First and Second Kind". Ing. - Arch. v. 43, London.
• Leipholz, H., 1977, "Direct Variational Methods and Eigenvalue Problems in Engineering". Nordholf International Publishing, Leyden, Netherland.
• Oliveira, A. M. and Altman, W., 1982, "The Quadratic Functional and its Applications to Blasius Problem", Tensor N. S. Chigasaki, v. 38.
• Oliveira, A.M., 1988, "Método da T ^_ Convolução". p. 132-133, III e IV ERMAC - INPE - São José dos Campos.
• Stakgold, I. A Boundary Value of Math. Physics. London.
• Terni, A.W., 1990, "Métodos dos Lagrangeanos Modificados e suas Aplicações na Formulação Variacional em Problemas Não-Conservativos". Tese de Mestrado, ITA
• Vainberg, M.M., 1973, "Variational Methods of Monotone Operators in the Theory of Nonlinear Equations", Wiley, New York.
• Weber, W. , 1848. Annalen der Phys, LXXIII, pp.193.

Publication Dates

• Publication in this collection
  15 Oct 2001
• Date of issue
  Dec 1999

History

• Received
  Mar 1997