Space-time finite element approximation andnumerical solution of hereditary linearviscoelasticity problems

Space-time finite element approximation andnumerical solution of hereditary linearviscoelasticity problems

Julia Orlik; Arina Ostrovska

Fraunhoferplatz 1, 67663 Kaiserslautern, Germany, E-mails: [e-mail] / [e-mail]

ABSTRACT

In this paper we suggest a fast numerical approach to treat problems of the hereditary linear viscoelasticity, which results in the system of elliptic partial differential equations in space variables, who's coefficients are Volterra integral operators of the second kind in time. We propose to approximate the relaxation kernels by the product of purely time- and space-dependent terms, which is achieved by their piecewise-polynomial space-interpolation. A priori error estimate was obtained and it was shown, that such approximation does not decrease the convergence order, when an interpolation polynomial is chosen of the same order as the shape functions for the spatial finite element approximation, while the computational effort is significantly reduced.

Mathematical subject classification: 22E46, 53C35, 57S20.

Key words: hereditary viscoelasticity; kern approximation by interpolation; space-time finite element approximation, stability and a priori estimate.

1 Introduction

Our task is to develop an approach for the numerical treatment of mathematical problems, which arise from considering the behavior of hereditary viscoelastic solids. These result in a system of elliptic partial differential equations in space variables, whose coefficients are Volterra integral operators of the second kind in time, which allow for weak-singular kernels, i.e.,

In Sections 2 and 3 a general mathematical model of the boundary value problem of the inhomogeneous hereditary ageing viscoelasticity is given in classical and weak formulations. The solvability of such a Volterra integral equation in Sobolev spaces and the stability of the solution with respect to the right-hand side is recalled here in Theorem 3.2 and proven in [3], [6], [5]. It will be used for the proof of Lemmas 6.1, 6.2, therefore is recalled here.

Our basic idea for the numerical solution of such a problem, was to treat the space and time dependence of the solution separately, with Finite Elementstechnique in x and with spline collocation in t, τ. Similar idea is presented in [13] with only difference that we allow for the non-convolutional and weakly singular relaxation kernels, i.e., our kernels must be only integrable and continuous after the integration and not necessary essentially bounded in the integrating time-variable as in [13].

The separate numerical space-time treatment of the problem can be performed trivially, if the time and space dependence in the instantaneous elastic coefficients a₀(x, t), relaxation kernels a(x, t,τ) and the external forces f(x, t) can be separated in a straightforward manner.

In Section 5 we suggest to approximate the integral kernels, out-of-integral terms and right-hand side in space by polynomial interpolation, possibly with the same shape functions that we use in the FE approximation of the solution, thus representing them by a product of purely time- and space-dependent terms. The idea of the kernel approximation by interpolation allows us to reduce the calculation time. It is widely used in spatial boundary integral equations of the kind

see, e.g., works of Hackbusch [21], [20].

Our next innovation is employing suitable quadrature formulas for the weakly singular kernel approximation in the well-known [7] collocation method for Volterra integral equations. Like in [25], where finite dimensional integral equations with weakly singular kernels are treated, we suggested to approximate the kernels by interpolation in singular points with the Lagrange canonical polynomials. This allows to avoid the singularity and analytically pre-calculate the weights in quadrature formulas.

We also use the fine property of the Volterra integral here, that if split the full integration interval on many subintervals and start the solution from the first subinterval, we are able to solve the problem on each subinterval separately and get a recurrent formula containing solution on all previous subintervals in the right-hand side.

In Section 6 the errors, introduced by the approximation of kernels, out-of-integral coefficients and external loads as well as the total error due to the numerical treatment are estimated. It is shown, that choosing an interpolation polynomial of the same or even one order less compared to the shape functions in the finite element approximation of the solution, we do not decrease the convergence order. Therefore we suggest the analyst to use the kernel approximation method, even though it requires more effort in preliminary work.

For the software realization of our numerical method we have chosen ANSYS as the basic simulation tool due to its extensive modeling capabilities and convenient user interface. The operations, that are not standard for ANSYS, like, for example, spline collocation in time or kernel approximation in space, were coded in separate procedures and integrated into the ANSYS environment as User Predefined Routines. A corresponding numerical example is considered in Section 7.

2 Definition of the problem

We consider a linear viscoelastic and aging (of the non-convolutional integral type) body, which is subject to some external loading. We denote the volume occupied by the body by Ω, which is assumed to be a Lipschitz domain.

We are going to consider the equilibrium equations for such a solid. Note that a viscoelastic solid is still a solid and therefore its deformation is slow and we restrict ourselves to the quasi-static case description, i.e., classical for the solid mechanics statement of problem, without the inertial term. A summation from 1 to n over repeating indices is assumed in all the present work, unless the opposite is stated.

with boundary conditions:

i = 1, 2, 3, ∀x Є Ω holding for any t Є [0, T].

are Volterra integral operators with kernels (x, t, τ); ₀(x, t) are instantaneous elastic coefficients (out-of-integral terms) and

f_i0 are components of a vector of external forces; ø_i(x, t) are components of a vector of boundary traction on the part ∂Ω_σ of the external boundary; ψ_i(x, t) are components of the displacement vector on the rest part ∂Ω_u of the boundary, n_h are components of the outer unit normal vector to the boundary of Ω. All functions are supposed to be continuous w.r.t. t Є [0, T] and sufficiently smooth w.r.t. x in domain Ω (for performing a partial integration).

The whole viscoelastic operator tensor is assumed to be symmetric at each point x Є Ω:

The tensor is additionally positive-definite, with elementsbounded at each point x Є Ω

for all Є and t Є [0, T], where the constants 0 < c₀< C₀ < ∞ are independent of x and t.

For isotropic materials we get:

Example 2.1.

(i) Often, the kernels (x, t, τ) are of the convolution type and are taken in the exponential form:

where the β_p(x) and the _p(x) are piecewise continuous functions for x Є Ω, often β_p are just constants;

(ii) The (x, t, τ) may also be kernels of the Abel type (e.g., relaxation kernels of concrete, rocks [1], polymers [2]):

with 0 < α, β, γ < 1. The , p = 1, 2, 3, are continuous in t and τ, and piece-wise continuous in x Є Ω.

3 Weak problem formulation and results on solvability and stability estimate

In this section we derive a weak problem formulation from the classical one, given by (2.1)-(2.3) in the previous section, by partial integration, and then assume general functional classes for its coefficients and right-hand sides.

In order to obtain the variational formulation, we multiply equation (2.1) by test functions v_i(x) Є 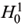(Ω,∂ Ω_u), i = 1,…, n, where 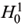(Ω, ∂ Ω_u) := {v Є H¹(Ω): v(x) = 0, x Є ∂ Ω_u}, and integrate over the whole domain Ω. Integrating by parts and taking into account boundary condition (2.2), we obtain:

If for equation (3.1) we take into consideration the boundary condition, we will obtain the following weak problem:

Find u_j Є H¹(Ω), j = 1,…, n, satisfying (2.2) and equation:

∀v_i Є (Ω,∂Ω_u), i = 1,…, n.

Definition 3.1 (General weak formulation). Consider the matrix of instantaneous elastic coefficients Є C([0,T]; L^∞(Ω)), the relaxation operators

, such that

(t, τ) = 0 ∀τ > t, and

Є C ([0, T]; L¹ ([0, T], L^∞(Ω))), and

f₀ := (f_i0)_nЄ C([0,T]; H^-1(Ω)),

the boundary tractionsø:= (ø_i)_nЄ C([0,T]; H^-1/2(∂Ω_σ)) and boundary displacements ψ:= (ψ_i)_nЄ C([0, T]; H^1/2(∂Ω_u)).

We define a weak solution of problem (2.1)-(2.3) as a vector-valued function u Є C([0, T]; H¹(W)), which can be represented in the form u = û + , where Є C([0,T]; H¹(Ω)) satisfies (

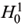|_{∂ Ωu}) = ψ and û_iЄ C([0, T]; (Ω, ∂Ω_u)), i = 1,…, n, satisfies the integral identity

for any v_iЄ 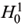(Ω,∂Ω_u). The right hand-side of (3.3) is, for all t Є [0, T], a linear functional on the (Ω, ∂Ω_u)

The space of linear bounded functionals on (Ω,∂ Ω_u) is denoted by H^-1(Ω).

We denote further

Obviously,

Note that a₀(û, v) and a(û, v) are bilinear forms on (Ω, ∂Ω_u) for every t and almost every τ. We can rewrite the weak formulation (3.3) as follows

Now let us rewrite equation (3.6) in the operator form. For this purpose we introduce the following notations:

A_0x(t), A_x(t, τ): (Ω,∂Ω_u) → H^-1(Ω) for all fixed t and almost all τ Є [0, T]. Now we can represent equation (3.3) in the form

where is an infinite dimensional integro-differential operator of the following form:

and the weak problem formulation (3.3) takes the form:

Equation (3.8) provides the most general form of the time-space integro-differential dependencies of the considered problem. The following theorem is used as an auxiliary result for showing the solvability of such equations.

Theorem 3.2 (Data stability). Let Ω⊂ ⁿ be a Lipschitz domain and ∂ Ω_u≠ ∂Ω, let A_0xЄ C([0,T]; ((Ω, ∂Ω_u), H^-1)), and let A_0x(t) be boundedly-invertible uniformly in [0,T], A_x(t, τ) = 0 ∀τ > t, A_xЄ C([0, T]; L¹([0, T], ((Ω, ∂Ω_u), H^-1))), and F Є C([0, T]; H^-1). Then there exists a unique global solution u of the problem

in C([0, T]; (Ω, ∂Ω_u)), which depends continuously on F, that is

where the constant C ₁ is independent of F, and if

, then

where

is some real-valued function, independent of f.

The proof of this theorem can be found in [3], [6].

Lemma 3.3. Let Ω be a Lipschitz domain in

ⁿ, the instantaneous elastic (out-of-integral) coefficients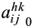 Є C([0,T]; L^∞(Ω)) satisfy the symmetry (2.5) and positivity condition (the first of (2.6)) with a constant c₀, and the relaxation kernels

^Є C([0,T], L¹([0,T], L^∞(Ω))) also satisfy the symmetry condition (2.5). Then

(i) A_0x belongs to C([0, T]; ((Ω,∂Ω_u), H^-1)), and A_0x(t) has an inverse operator (t) ∀t Є [0, T]. This inverse operator is uniformly bounded in [0, T], that is, the following estimate

holds for any t Є [0, T], and c₀is independent from t.

(ii) A_x(t, τ) satisfies the following estimate

∀t and almost all τ Є [0, T]. Furthermore, the condition

See [3], [6] for proof.

Lemma 3.2. In both cases of Example 2.1,

See [3], [6] for proof.

Remark 3.5. Consider the weak problem given by Definition 3.1. The functional defined by (3.4) is a continuous functional, satisfying the following estimate

where C depends on Ω, ∂Ω_σ, max_i,j,h,k.

See [3], [6], [10] for proof.

4 Preliminaries w.r.t. approximation and interpolation

We construct on domain a quasi-uniform triangular/tetrahedral space mesh of N_el elements and denote each element j of Ω by Ω_j. We denote h := max_j (diam Ω_j) . Then, we perform the semi-discrete (spatial) FE approximation of the solution in space by:

where N_j(x) are shape functions, n_nodes denotes the number of nodes in each finite element and P_r is a projection on the space of polynomials of degree at most r.

The following standard (see, e.g. [17] or (32), Th. 5 in [13]) error estimate

or

is known for the solution u of problem (2.1)-(2.3), and its semi-discrete projection u_h defined by (4.1), if the triangulation of Ω is quasi-uniform. It is known from the standard theory of elliptic second order problems [12], that if Ω is C^1,1 convex domain in ⁿ, ∂Ω_u is non-empty and the coefficients are piece-wise smooth in the space variable then the solution of the problem (2.1)-(2.3) is regular in H² and, according to [12], Chap. 8, Th. 8.12, using (3.14) (assuming ø, ψ = 0),

Furthermore, if Ω has a C^r+1-boundary, then the problem (2.1)-(2.3) is H^r+1-regular, and,

Remark 4.1. Note only that this is difficult to reach for r higher value than 1, since C³-regular boundary may arise some problems with a suitable triangulation at the boundaries. Therefore the best choice for the FE-approximation are linear shape functions.

Using (4.2) and the stability estimate (4.4), (3.10), (3.14), we estimate the error of the spatial semi-discrete FE-discretization:

or

Then we can refer to Theorem 2 from [13] or Theorem 6 from [15] for discrete data stability estimate

We should only replace in its proof the estimate of the history term by the following estimate

Further, we divide the time interval [0,T] by (n₁ + 1) points 0 = t₀ < t₁ < … < t_n1 = T and denote q := max_i |t_i - t_i-1|. In the next step, we perform fully discrete polynomial approximation of the n-dimensional vectors U_j = (U_{j 1},…, U_{j n}), j = 1,…, n_nodes, in time:

where are polynomials of the power p Є [0, ∞) on intervals [t_i, t_i+1] ≠ [0, T]. Thus, we obtain the complete space-time approximation π_p P_r u of the exact solution u(x, t).

According to Lemma 12 from [14],

where B = {H¹(Ω), L²(Ω)}, = p + 1 > 0 and q := max_i |t_i - t_i-1|, i = 1,…, n₁. The same result is presented in [8] (Theorem 1.1) and [21] (Theorems 4.4.7 and 4.3.15) for spline collocation approximation (4.10) of finite dimensional functions with collocation parameters {c_k} chosen as equidistant points in [0,1].

Remark 4.2. In general, for p > 1, the stability constant C_π depends upon the numerical solution and discretization ||π_p||. But for piece-wise constant or linear interpolation, C_π is an independent constant (see Sec. 4.4 in [21] orLem. 12 in [14]).

We restrict ourselves on the case p < 1 in this paper.

Remark 4.3. Estimate (4.11) again requires a higher regularity (now w.r.t. time) as it is assumed in Section 3. Nevertheless, looking through the proofs (see [1]) of statements recalled in Section 3, one can see that all estimates could be justified also for right-hand side functions, integral kernels (after integration) and instantaneous elastic coefficient from C¹([0, T]).

In the next step we analyze the space-time dependencies in the out-of-integral (instantaneous elastic) coefficients, the integral kernels and the right-hand side of the problem (2.1)-(2.3). In our following considerations we will represent the integral kernels in the form:

where (x, t, τ) are the well-behaved parts of the kernel, normally piecewise-smooth and bounded, and (t, τ) are singular parts.

If it is possible to separate the space and time dependence in the non-singular part of the kernels, as well as in the out-of-integral coefficients and the right-hand side functions, and use their global stiffness matrix (matrices) as the constant coefficient matrix in constructing the system of finite dimensional integral equations later on.

If such separation is not applicable, we are forced to discretize the time interval and carry out the series of FEM analyzes for large number of values of t_m and τ_l. The stiffness matrices, which we obtain, are used afterwards for approximating the coefficient matrices of the resulting system of integral equations.

It is obvious, that for the second, more complicated case, the time interval discretization points must be chosen very carefully in order to minimize the number of spatial analyzes on the one hand (note that even a single run of the FEM package on a non-trivial geometry can appear extremely time- and resource-consuming), and on the other hand, to capture all the non-smoothness properties of the kernel, like oscillations, jumps etc.

In the sections below we suggest an approach to the numerical treatment of the equations with relaxation kernels (x, t, τ), the instantaneous elastic coefficients (out-of-integral terms) 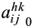(x, t), components of vectors of external forces f_i0 and boundary traction ø_i(x, t), with inseparable time and space dependencies. Let us recall the following error estimate for multidimensional interpolation from [22].

Theorem 4.4. Let Ω ≠ ⁿ, f Є C^r+1(Ω) and S^r f(·) be its unique interpolation by Lagrange polynomials of degree < r taken on the triangular/tetrahedral discretization (Ω_j)_j=1,…, _Nel of domain Ω. Let further N = N(r) = dim S^r be the number of interpolation points in each Ω_j, j = 1,…,N_el. Then the following interpolation estimate

is valid, where C = C(r, n) and

where the notation D^r f = , α₁+ ¼ + α_n = r is used.

Furthermore, if fЄ H^r+1(Ω), and S^rЄ (H^r+1(Ω), H^m(Ω))

These estimates can be generalized for the essentially bounded (like in [13], [15]) or continuous on a closed interval, i.e., bounded (like in our case) in time semi-discrete (spatial) approximations.

5 Spatial approximation via interpolation and subsequent FE/collocation methods

By the space-time approximations (4.1) and (4.10) we reduce the infinite dimensional system of integral equations (1.1) in Hilbert spaces to the system of linear algebraic equations and the viscoelastic problem with memory (1.2) to the system of recurrent pure elastic problems in this section.

Suppose that ψ ≡ 0, and functions , , 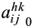f_i0 and ø _i are m + 1 time differentiable in Ω. We suggest to approximate all these terms with respect to x Є Ω by continuous functions that are piecewise-polynomial on the finite elements Ω_p, p = 1,…,N_el, i.e.

where N_el is the number of elements in the model, x_q is the node of the p-th element, χ _p is a characteristic function on the elements, i.e.:

and (x) is a Lagrange polynomial of power m in the q-th node of the p-th element.

Performing FE-approximation (4.1), we obtain entries of the global stiffness matrix

where i, j = 1,…,n, stand for displacement vector components, u, l are global numbers of the nodes belonging to element p, and Φ_{nd, γ}(x_q, t, [u_d]) are integrals

with n = 0,…n₁ and γ standing for a generic 4-index.

Now, let us apply approximation (5.1) to the instantaneous elastic coefficients 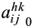(x, t) and then apply the Finite Element approximation (4.1) to the out-of-integral term of operator equation (3.6). Thus we eliminate the space dependence, and obtain elements of the out-of-integral stiffness matrix

Finally, we calculate the elements entries of the global load vector. For this reason we refer to (3.4), keeping in mind that we let for simplicity ψ(x, t) ≡ 0.

Collecting these element stiffness matrices and load vectors to the global ones by the standard assembly procedure, we can rewrite the variational statement of the problem (3.1) in the form:

Further, we look for the solution of (5.6) recurrently in each subinterval using (4.10), which can be done by standard collocation procedure.

Remark 5.1. Note that we can replace (x) in definitions (5.2), (5.4), (5.5) by N_q(x), if the shape functions approximating the solution and the Lagrange shape functions (x), approximating the inhomogeneous coefficients and the external loading, all are of the same order.

In most applications the integrals (5.3) occurring in the collocation equation (5.6) cannot be evaluated analytically. Besides, the term β(t, τ) possesses a weak singularity in the end of every subinterval (see (2.9)). One is forced to resort the collocation algorithm given in [7] to employing suitable quadrature formulae for kernel approximation. Thus, we suggest here to use the Lagrange canonical polynomials

for collocation parameters {c_j} with 0 < c₁ < … < c_p+1< 1 as weights for quadrature approximation of integrals (5.3), i.e., replace (5.3) by the sum:

with the quadrature weights given by

A similar idea was also presented in [25].

Example 5.2. Let β(t, s) ≡ 1. Then we are in a framework of the standardcollocation and

Example 5.3. Let β(t, s) = (t - s)^-α and let the discretization by t_n, n = {0, n₁} be equidistant with step size q. Then

This integral could be analytically taken in the form of a hypergeometric series (see [23]). However it can be reduced to the finite expression through Euler's Γ- or - functions only for n - i + c_j = 1. Therefore, we prefer to avoid the weak singularity by partial integration

The detailed recurrent formulas for the weights can be found in [24].

6 A priori error estimates

Let us first suppose that the instantaneous elastic coefficients 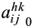as well as the external loads f_i0 and ø_i are either space-independent functions or change homogeneously in space, i.e. they are represented as a product of purely space and time dependent functions respectively. Furthermore, we suppose, that Є L¹([0, T]), i.e., the weak singular part of integral kernels is space independent, Є C([0, T] × [0, T], C^m+1 (Ω)). We apply the suggested in Section 5 approximation in space by interpolation to the relaxation kernels only. Let

where S^m(x, t, τ) is the approximation of the non-singular part of the kernels, defined by (5.1), and u_S denotes the solution of our problem (3.9) corresponding to this approximation. We introduce the error in the solution caused by the kernel approximation by interpolation as:

Lemma 6.1. The error in the solution caused by kernel approximation (5.1) isof the same order as the error of kernel approximation itself, i.e.

for any t Є [0,T], where

Proof. To begin with, let us represent equation (3.9) in the form:

Similarly, we can write for u_S(t):

The difference u - u_S should then satisfy equation

Owing to Theorem 3.2, (4.8), the error (6.3) can then be estimated as follows:

Let now the instantaneous elastic coefficients 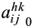and the external loads f_i0 and ø_i also possess inseparable time-space dependencies and 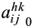, f_i0 and ø_i belong to C([0, T], C^m+1(Ω)). So, we apply the approximation S^m, defined by (5.1), to these terms too. We define, additionally to (6.1), (6.2),

where S^m is the approximation defined by (5.1), and u_S denotes the solution of (3.9) corresponding to this approximation.

Lemma 6.2. The error in the solution of (3.9) caused by approximations S^m

, S^m

, S^m f_i0 and S^m+1ø_i is again of the order O(h^m+1), i.e.,

for any t Є [0, T].

Proof. Consider again equations (6.5) and

We estimate the error on the same way as in previous lemma just extending the proof by the triangle inequality:

First we estimate

and, according to Remark (3.5)

Let us estimate the term now:

Application of Theorem 4.4 to each term of (6.11), to (6.12) and to (6.13) completes the proof.

The following lemma gives the a priori estimate for the total solution error.

Theorem 6.3 (A priori error estimate). The error estimate satisfies:

Proof. Using triangle inequality, we can see that:

The estimates for the first term in the right-hand side are given by (6.4), (6.9), for the second by (4.2) and (4.6) for L²- and H¹-norms respectively, and for the third term by (4.11).

Thus, we can conclude that the error, introduced by spatial approximation of relaxation kernels, instantaneous elastic coefficients and external loads, does not increase the total error, if m > r. On the other hand, it significantly simplifies the calculation procedure, allowing us to significantly reduce the computations of the spatial finite element analysis.

7 Numerical example

Consider the homogeneous isotropic viscoelastic prismatic rod of length ℓ, as shown in Figure 1.

It is subject to stretching under its own weight and under an external tension pressure p, homogeneously distributed over its lower end. The rod is rigidly fixed in the middle point A = (0, 0, 0) on its upper face. Besides, the zero displacement constraints in vertical direction are applied to the circle of diameter m, which completely belongs to the upper face of the rod.

Consider the system of equilibrium equations (2.1)-(2.3) under isotropy condition (2.7), and switch over to Poisson's ratio and Young's modulus through the relation:

We assume further that the Poisson's ratio ν is time-independent and that the Young's modulus E is taken in the form of the following Volterra integral operator

Now, the system of equilibrium equations (2.1)-(2.3) can be rewritten as follows:

with boundary conditions:

holding for any t Є [0, T]. Here

where ρ is the material density, and we choose

Since the right-hand side of our system can be represented as a product of a purely space- and time-dependent function, and the kernel (7.9) of operator (7.2) is space-independent, the solution of the problem (7.3)-(7.7) will be of the form:

We rewrite our system as:

Then the pair of equations, consisting of the purely spatial one:

and the temporal one:

can be solved analytically to yield the desired solution:

for the spatial part of the solution, and

For a numerical simulation of the system's space-dependent part we used the ANSYS Finite Element package. Since the ANSYS element library does not contain elements supporting materials with weakly singular kernels, we combined ANSYS with the collocation method implemented in an own fortran code based on the algorithm from [8]. The latter algorithm was modified to allow for weak-singular kernel parts as well as a coefficient matrix in front of the out-of-integral term.

The FEM discretization of w.r.t. the space variable is obtained as the global stiffness matrix of the problem with appropriate material properties, and the one for the right-hand side as a global load vector. For the extraction of the global stiffness matrix from ANSYS in a text format, we modified rdsubs.F code, taken from the ANSYS distribution medium and incorporated into original ANSYS as a User Predefined Routine (UPF). Thus, we reduced the infinite-dimensional system of the Volterra integral equations to a finite-dimensional one. Then, the obtained integral equation system was solved numerically with the spline collocation method described in Section 5. Finally the numerical solution for the system of integral equations was obtained by iteratively solving a system of linear algebraic equations with help of the conjugate gradient method, as u_ij = u_i(t_j), j = 0,…, n₁, i = 1, …, 3N, where n₁ is the number of discretization points for the time interval and N is the number of nodes in the finite element discretization of the body.

7.1 Convergence in time

To test the temporal convergence of the collocation method, we solve both problems, (7.14) and (7.15), on the unit time interval with five collocation points on a unit subinterval and compare the analytical u₂(t) and numerical U₂(t) solutions in the arbitrary chosen time point T = . The summary of numerical performance is presented in Table 1.

7.2 Spatial and full convergence

The following parameter set: E₀ = 8.5 ·10¹⁰ Pa, ν = 0.16, ρ = 1.2770 kg/m³, p = -10·10⁷ Pa, m = 1 cm, l = 10 cm was used for a numerical example. To perform the numerical simulation with ANSYS, we took advantage of the symmetry of the modeled body and therefore considered only a quarter of it (see Fig. 3). The body has been discretized with 244 elements, 620 nodes. The summary of successive spatial and temporal numerical performances of ANSYS and the collocation fortran-routine is presented in Tables 2 and 3.

Received: 31/X/06. Accepted: 27/III/08.

#685/06.

• [1] Yu. N. Rabotnov, Creep problems in structural members Nord-Holland Publishing Company, 1969.
• [2] P. Hubsch, S. Seibold, J. Orlik and J. Middleton, Identification of the visco-elastic properties of curing dental composites Recent Advances in Computer Methods in Biomechanics and Biomedical Engineering, Lisbon, October 1999.
• [3] J. Orlik, Transmission and Homogenization in Hereditary Viscoelasticity with Aging and Shrinkage Shaker Verlag, 2000.
• [4] J. Orlik and S.E. Mikhailov, Homogenization in Integral Viscoelasticity ZAMM, 81 (Suppl. 4) (2001), 983-984.
• [5] J. Orlik, Homogenization for Viscoelasticity Progress in industrial mathematics at ECMI 2000, Angelo Marcello Anile… ed., Berlin, Heidelberg, New York, …: Springer, pp. 618-624, 2002.
• [6] J. Orlik, Existence and stability estimate for the solution of the ageing hereditary linear viscoelasticity problem, submitted to Journal of Math. An. and Appl. (JMAA).
• [7] J.G. Blom and H. Brunner, The Numerical Solution of Nonlinear Volterra Integral Equations of the Second Kind by Collocation and Iterated Collocation Method SIAM J. Sci. Stat. Comput., 8(5), September 1987.
• [8] J.G. Blom and H. Brunner, Algorithm 689: Discretized Collocation And Iterated Collocation For Nonlinear Volterra Integral Equations of the Second Kind ACM Transactions on Mathematical Software, 17(2), June 1991.
• [9] Christophe T. Baker, An Introduction to the Numerical Treatment of Volterra and Abel-type Integral Equations Manchester, Dep. of Math., Univ., 1982.
• [10] O.A. Oleinik, A.S. Schamaev and G.A. Yosifian, Mathematical problems in elasticity andhomogenization North-Holland Publishing Company - Amsterdam/ London/ New York/ Tokyo, 1992.
• [11] Yu. Rabotnov, L. Papernik and E.N. Zvonov, Tables of the Fractional Exponentional Functions of Negative Parameters and its integral (In Russian), Moskaw, Nauka, 1969.
• [12] D. Gilbarg and N.S. Trudinger, Elliptic Partial Differential Equation of Second Order Springer-Verlag, 1983.
• [13] Simon Shaw and J.R. Whiteman, A Posteriori Error Estimate For Space-Time Finite Element Approximation of Quasistatic Hereditary Linear Viscoelasticity Problems March 2003.
• [14] Simon Shaw and J.R. Whiteman, Numerical Solution of Linear Quasistatic Hereditary Viscoelasticity Problems I: A Priori Estimates 08.01.1999, BICOM: http://www.brunel.ac.uk/icsrbicm
• [15] Simon Shaw and J.R. Whiteman, Numerical Solution of Linear Quasistatic Hereditary Viscoelasticity Problems SIAM J. Numer. Anal., 38(1) (2000), 80-97, BICOM: http://www.brunel.ac.uk/icsrbicm
• [16] K. Eriksson and C. Johnson, Adaptive finite element methods for parabolic problems. I: a linear model problem SIAM J. Numer. Anal., 28 (1991), 43-77.
• [17] S. Brenner and L.R. Scott, The Mathematical Theory of Finite Element Methods Springer, New York, 1994.
• [18] L.R. Scott and S. Zhang, Finite element interpolation of nonsmooth functions satisfying boundary conditions Math. Comp., 54 (1990), 483-493.
• [19] T. Dupont and R. Scott, Polynomial approximation of functions in Sobolev spaces Math. Comp., 34 (1980), 441-463.
• [20] W. Hackbusch and S. Boerm, H² - Matrix Approximation of Integral Operators by Interpolation Max-Planck-Institut Leipzig, April 19, 2004.
• [21] W. Hackbusch, Integralgleichungen, Theorie und Numerik B.G. Teubner Stuttgart, 1997.
• [22] P.G. Ciarlet and P.A. Raviart, General Lagrange and Hermite interpolation in Rⁿ with applications to finite element method Arch. Rat. Mech. Anal., 46 (1972), 177-199.
• [23] I.S. Grandshteyn and I.M. Ryzhik, Table of integrals, series and products Transl. from Russian, Acad. Pr. New York, 1979.
• [24] C.T.H. Baker, The Numerical Treatment of Integral Equations Claredon Press, Oxford, 1977.
• [25] Annamaria Palamara Orsi, Product Integration for Volterra Integral Equations of the Second Kind With Weakly Singular Kernels Math. Comp., 65, 1201-1212, July 1996.

Publication Dates

• Publication in this collection
  21 July 2008
• Date of issue
  2008

History

• Accepted
  27 Mar 2008
• Received
  31 Oct 2006