Picard and Adomian methods for quadratic integral equation

Picard and Adomian methods for quadratic integral equation

El-Sayed A.M.A.^I; Hashem H.H.G.^II; Ziada E.A.A.^II

^IFaculty of Science, Alexandria University, Alexandria, Egypt

^IIFaculty of Engineering, Mansoura University, Mansoura, Egypt E-mails: [e-mail] / [e-mail] / [e-mail]

ABSTRACT

We are concerning with two analytical methods; the classical method of successive approximations (Picard method) [14] which consists the construction of a sequence of functions such that the limit of this sequence of functions in the sense of uniform convergence is the solution of a quadratic integral equation, and Adomian method which gives the solution as a series see ([1-6], [12] and [13]). The existence and uniqueness of the solution and the convergence will be discussed for each method.

Mathematical subject classification: Primary: 39B82; Secondary: 44B20, 46C05.

Key words: quadratic integral equation, Picard method, Adomian method, continuous unique solution, convergence analysis, error analysis.

1 Introduction

Quadratic integral equations (QIEs) are often applicable in the theory of radiative transfer, kinetic theory of gases, in the theory of neutron transport and in the traffic theory. The quadratic integral equations can be very often encountered in many applications.

The quadratic integral equations have been studied in several papers andmonographs (see for examples [7-11] and [16-22]).

The Picard-Lindelof theorem for the initial value problem

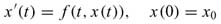
was proved in [14] and the solution can be shown as the limit of constructed sequence.

The existence of continuous solution of the nonlinear quadratic integral equation

was proved in [18] by using Tychonov fixed point theorem where f and g satisfy Carathéodory condition.

In this work, we will prove the existence and the uniqueness of continuous solution for (1) by using the principle of contraction mapping. Also, we are concerning with the two methods; Picard method and Adomian method.

2 Main Theorem

Now, equation (1) will be investigated under the assumptions:

is continuous on I where I = [0,1];

are continuous and there exist positive constants M₁ and M₂ such that |g(t,x)| < M₁ and |f(t,x)| < M₂ on D;

(iii) f,g satisfy Lipschitz condition with Lipschitz constants L₁ and L₂ such that,

Let C = C(I) be the space of all real valued functions which are continuous on I.

Define the operator F as

Theorem 1. Let the assumptions (i)-(iii) be satisfied. If h = (L₁M₂+L₂M₁) < 1, then the nonlinear quadratic integral equation (1) has a unique positive solution x∈C.

Proof. It is clear that the operator F maps C into C.

Now define a subset S of C as

Then the operator F maps S into S, since for x ∈ S

Moreover it is easy to see that S is a closed subset of C. In order to show thatF is a contraction we compute

Since

then F is a contraction and F has a unique fixed point in S, thus there exists a unique solution for (1). □

3 Method of successive approximations (Picard method)

Applying Picard method to the quadratic integral equation (1), the solution is constructed by the sequence

All the functions x_n(t) are continuous functions and x_n can be written as a sum of successive differences:

This means that convergence of the sequence x_nis equivalent to convergence of the infinite series Σ(x_j-x_j-1) and the solution will be,

i.e. if the infinite series Σ(x_j-x_j-1) converges, then the sequence x_n(t) will converge to x(t). To prove the uniform convergence of {x_n(t)}, we shall consider the associated series

From (2) for n = 1, we get

and

Now, we shall obtain an estimate for x_n(t)-x_n-1(t), n > 2

using assumptions (ii) and (iii), we get

Putting n = 2, then using (3) we get

Repeating this technique, we obtain the general estimate for the terms of the series:

Since (L₁M₂+L₂M₁) < 1, then the uniform convergence of

is proved and so the sequence {x_n(t)} is uniformly convergent.

Since f(t,x) and g(t,x) are continuous in x, then

thus, the existence of a solution is proved.

To prove the uniqueness, let y(t) be a continuous solution of (1). Then

and

using assumptions (ii) and (iii), we get

But

and using (4) then we get

Hence

which completes the proof. □

When g(t,x) = 1, then M₁ = 1 and L₁ = 0 and we obtain the original Picard theorem [14] and [15].

Corollary 1. Let the assumptions of Theorem 1 (with g(t,x) = 1) be satisfied. If L₂ < 1, then the integral equation

has a unique continuous solution.

4 Adomian Decomposition Method (ADM)

The Adomian decomposition method (ADM) is a nonnumerical method forsolving a wide variety of functional equations and usually gets the solution in a series form.

Since the beginning of the 1980s, Adomian ([1-6] and [12-13]) has presented and developed a so-called decomposition method for solving algebraic, differential, integro-differential, differential-delay, and partial differential equations. The solution is found as an infinite series which converges rapidly to accurate solutions. The method has many advantages over the classical techniques, mainly, it makes unnecessary the linearization, perturbation and other restrictive methods and assumptions which may change the problem being solved, sometimes seriously. In recent decades, there has been a great deal of interest in the Adomian decomposition method. The method was successfully applied to a large amount of applications in applied sciences. For more details about the method and its application, see ([1-6] and [12-13]).

In this section, we shall study Adomian decomposition method (ADM) for the quadratic integral equation (1).

The solution algorithm of the quadratic integral equation (1) using ADM is,

where A_iand B_i are Adomian polynomials of the nonlinear terms g(t,x) and f(s,x) respectively, which have the form

and the solution will be,

4.1 Convergence analysis

Theorem 2. Let the solution of the QIE (1) exists. If |x₁(t)| < l,l is a positive constant, then the series solution (9) of the QIE (1) using ADM converges.

Proof. Define the sequence {S_p} such that,

is the sequence of partial sums from the series solution , and we have

Let S_p and S_q be two arbitrary partial sums with p > q. Now, we are going to prove that {S_p} is a Cauchy sequence in this Banach space E.

Let p = q+1 then,

From the triangle inequality we have,

Now 0 < h < 1, and p > q implies that (1-h^p-q) < 1. Consequently,

converges.

□

4.2 Error analysis

Theorem 3. The maximum absolute truncation error of the series solution (9) to the problem (1) is estimated to be,

Proof. From Theorem 2 we have,

so, the maximum absolute truncation error in the interval I is,

and this completes the proof. □

5 Numerical Examples

In this section, we shall study some numerical examples and applying Picard and ADM methods, then comparing the results.

Example 1. Consider the following nonlinear QIE,

and has the exact solution x(t) = t².

Applying Picard method to equation (10), we get

and the solution will be,

Applying ADM to equation (10), we get

where A_i are Adomian polynomials of the nonlinear term x², and the solution will be,

Table 1 shows a comparison between the absolute error of Picard (when n = 5) and ADM solutions (when q = 5).

Example 2. Consider the following nonlinear QIE,

and has the exact solution x(t) = t³.

Applying Picard method to equation (11), we get

and the solution will be,

Applying ADM to equation (11), we get

where A_i and B_i are Adomian polynomials of the nonlinear terms x² and x³ respectively, and the solution will be,

Table 2 shows a comparison between the absolute error of Picard (when n = 3) and ADM solutions (when q = 3).

Example 3. Consider the following nonlinear QIE [9],

Applying Picard method to equation (12), we get

and the solution will be,

Applying ADM to equation (12), we get

where A_i are Adomian polynomials of the nonlinear term cos ()and the solution will be,

Table 3 shows a caparison between ADM and Picard solutions.

Example 4. Consider the following nonlinear QIE [8],

Applying Picard method to equation (13), we get

and the solution will be,

Applying ADM to equation (13), we get

where A_i are Adomian polynomials of the nonlinear term ln(1+s|x(s)|) and the solution will be,

Table 4 shows a caparison between ADM and Picard solutions.

6 Conclusion

We used two analytical methods to solve QIEs; Picard method and ADM, from the results in the tables we see that Picard method gives more accurate solution than ADM.

Received: 07/VI/09

Accepted: 02/XII/09.

#CAM-118/09

• [1] G. Adomian, Stochastic System Academic Press (1983).
• [2] G. Adomian, Nonlinear Stochastic Operator Equations Academic Press, San Diego (1986).
• [3] G. Adomian, Nonlinear Stochastic Systems: Theory and Applications to Physics Kluwer (1989).
• [4] G. Adomian, R. Rach and R. Mayer, Modified decomposition J. Appl. Math. Comput., 23 (1992), 17-23.
• [5] K. Abbaoui and Y. Cherruault, Convergence of Adomian's method Applied to Differential Equations. Computers Math. Applic., 28 (1994) 103-109.
• [6] G. Adomian, Solving Frontier Problems of Physics: The Decomposition Method. Kluwer (1995).
• [7] J. Banaś, M. Lecko and W.G. El-Sayed, Existence Theorems of Some Quadratic Integral Equation J. Math. Anal. Appl., 227 (1998), 276-279.
• [8] J. Banaś and A. Martinon, Monotonic Solutions of a quadratic Integral Equation of Volterra Type Comput. Math. Appl., 47 (2004), 271-279.
• [9] J. Banaś, J. Caballero, J. Rocha and K. Sadarangani, Monotonic Solutions of a Class of Quadratic Integral Equations of Volterra Type. Computers and Mathematics with Applications, 49 (2005), 943-952.
• [10] J. Banaś, J. Rocha Martin and K. Sadarangani, On the solution of a quadratic integral equation of Hammerstein type. Mathematical and Computer Modelling, 43 (2006), 97-104.
• [11] J. Banaś and B. Rzepka, Monotonic solutions of a quadratic integral equations of fractional order. J. Math. Anal. Appl., 332 (2007), 1370-11378.
• [12] Y. Cherruault, Convergence of Adomian method. Kybernetes, 18 (1989), 31-38.
• [13] Y. Cherruault, G. Adomian, K. Abbaoui and R. Rach, Further remarks on convergence of decomposition method. Int. J. of Bio-Medical Computing., 38 (1995), 89-93.
• [14] R.F. Curtain and A.J. Pritchard, Functional Analysis in Modern Applied Mathematics. Academic Press (1977).
• [15] C. Corduneanu, Principles of Differential and integral equations. Allyn and Bacon. Hnc., New York (1971).
• [16] A.M.A. El-Sayed, M.M. Saleh and E.A.A. Ziada, Numerical and Analytic Solution for Nonlinear Quadratic Integral Equations. Math. Sci. Res. J., 12(8) (2008), 183-191.
• [17] A.M.A. El-Sayed and H.H.G. Hashem, Carathéodory type theorem for a nonlinear quadratic integral equation. Math. Sci. Res. J., 12(4) (2008), 71-95.
• [18] A.M.A. El-Sayed and H.H.G. Hashem, Integrable and continuous solutions of nonlinear quadratic integral equation. Electronic Journal of Qualitative Theory of Differential Equations, 25 (2008), 1-10.
• [19] A.M.A. El-Sayed and H.H.G. Hashem, Monotonic positive solution of nonlinear quadratic Hammerstein and Urysohn functional integral equations. Commentationes Mathematicae, 48(2) (2008), 199-207.
• [20] A.M.A. El-Sayed and H.H.G. Hashem, Weak maximal and minimal solutions for Hammerstein and Urysohn integral equations in reflexive Banach spaces. Differential Equation and Control Processes, 4 (2008), 50-62.
• [21] A.M.A. El-Sayed and H.H.G. Hashem, Monotonic solutions of functional integral and differential equations of fractional order. E.J. Qualitative Theory of Diff. Equ., 7 (2009), 1-8.
• [22] A.M.A. El-Sayed and H.H.G. Hashem, Solvability of nonlinear Hammerstein quadratic integral equations. J. Nonlinear Sci. Appl., 2(3) (2009), 152-160.

Publication Dates

• Publication in this collection
  22 Nov 2010
• Date of issue
  2010

History

• Accepted
  02 Dec 2009
• Received
  07 June 2009