Chain control sets and fiber bundles

Abstract

Let S be a semigroup of homeomorphisms of a compact metric space M and suppose that <img border=0 id="_x0000_i1026" src="../../../../../img/revistas/cam/v22n3/a03img86.gif" align=absmiddle>is a family of subsets of S. This paper gives a characterization of the <img border=0 id="_x0000_i1027" src="../../../../../img/revistas/cam/v22n3/a03img86.gif" align=absmiddle>-chain control sets as intersection of control sets for the semigroups generated by the neighborhoods of the subsets in <img border=0 id="_x0000_i1028" src="../../../../../img/revistas/cam/v22n3/a03img86.gif" align=absmiddle>. We also study the behavior of <img border=0 id="_x0000_i1029" src="../../../../../img/revistas/cam/v22n3/a03img86.gif" align=absmiddle>-chain control sets on principal bundles and their associated bundles.

semigroups; control sets; chain control sets; principal bundles; associated bundles

Chain control sets and fiber bundles

Carlos J. Braga Barros^*

Departamento de Matemática, Universidade Estadual de Maringá, 87020-900 Maringá, PR, Brasil, E-mail: [e-mail]

ABSTRACT

Let S be a semigroup of homeomorphisms of a compact metric space M and suppose that is a family of subsets of S. This paper gives a characterization of the -chain control sets as intersection of control sets for the semigroups generated by the neighborhoods of the subsets in . We also study the behavior of -chain control sets on principal bundles and their associated bundles.

Mathematical subject classification: 93B03, 93B05.

Key words: semigroups, control sets, chain control sets, principal bundles, associated bundles.

1 Introduction

The concept of chain control set for control systems was introduced by Colonius and Kliemann [4], [7]. These sets appear as a tool for the analysis of the asymptotic properties of control systems (see [4], [5], [6], [7]). Extending this notion for general classes of semigroups Braga Barros and San Martin [2] defined chain control sets for a family of subsets of a semigroup acting on a homogeneous space. In that paper chain control sets were characterized as intersection of control sets for the semigroups generated by the neighborhoods of the subsets in the family. This paper shows a similar result for semigroups of homeomorphisms of a compact metric space. The approach is different from that of [2] because the semigroup may have empty interior in the group of homeomorphisms. An important fact which permits our generalization of [2] is that the hypothesis H defined there can be extended to semigroup of homeomorphisms acting on a compact metric space.

Apart from this general characterization of chain control sets we also study chain control sets on fiber bundles. The action of semigroups in fiber bundles arises naturally in many contexts. For instance in nonlinear control systems the linearized flow evolves on a fiber bundle over the state space of the system (see [4], [7]). The action of semigroups of diffeomorphisms on fiber bundles were studied by Braga Barros and San Martin [3]. In [3] the control sets were described from their projections onto the base space and their intersections with the fibers.

In this paper we pursue the same kind of results for chain control sets. We show that a chain control set in the total space of a fiber bundle projects inside a chain control set in the base space. On the other hand, we also show that a chain control set in the fiber is contained in a chain control set in the total space. Assuming that the structural group of a principal bundle is compact we use the characterization of chain control sets as intersections of control sets to show that the inverse image by the projection of a chain control set in the base space of the fiber bundle is a chain control set in the total space.

We believe that these topological results are useful for further developments of the dynamical aspects of control systems.

2

-chain control sets

In this section we recall the concept of a chain control set associated with a family of subsets of a semigroup. We refer to [2] for the definition of chain control sets for semigroup actions and corresponding results on homogeneous spaces of Lie groups.

For a semigroup of homeomorphisms of a compact metric space it is shown, under certain conditions, that a chain control set is the intersection of control sets for the semigroups generated by the neighborhoods of the subsets in the family.

We begin by assuming that S is a semigroup of homeomorphisms of a compact metric space M. From now on, and in the whole paper we assume that S and S^–1 have the accessibility property, that is, int (Sx) ¹ Æ and int (S^–1x) ¹ Æ for every x Î M.

We fix a distance d on M and define chain control sets for a family of subsets of S.

Definition 1. Let be a family of subsets of S. Take x, y Î M, a real e > 0 and A Î . A (S, e, A)-chain from x to y consists of points x₀ = x, x₁,¼, x_n–1, x_n = y in M and f₀,¼, f_n–1Î A such that d(f_j(x_j), x_j+1) < e for j = 0,¼, n – 1. A subset E Ì M is called a -chain control set if it satisfies

1. int(E) ¹ Æ.

2. For every x, y Î E, there exists a (S, e, A)-chain from x to y, for every e > 0 and A Î .

3. E is maximal satisfying these properties.

It is easy to see that the notion of -chain control set does not change if an equivalent distance is considered. Also, it follows from the third condition that two -chain control sets are either disjoint or coincident. Furthermore, an application of Zorn's Lemma shows that any subset satisfying the first two conditions in the Definition 1 is contained in a -chain control set.

Next, we show that effective control sets (for the theory of control sets we refer to [11], [7]) are contained in -chain control sets. We need to impose the following conditions on .

Definition 2. Let be a family of subsets of a semigroup S. We say that satisfies property P_l (respectively P_r) if for every f, y Î S, f ¹ 1 and every A Î , there exists a positive integer n such that fⁿy Î A (respectively yfⁿ Î A).

Let's denote by S_A the semigroup generated by a subset A Ì S.

Proposition 1. Assume that

is a family of subsets of a semigroup S satisfying the properties P_l and P_r and take A Î . Let D be an effective control set for S. Then D Ì cl(S_Ax) for any x Î D.

Proof. Take x, y Î D. Let us show that y Î cl (S_Ax). Let D₀ = {x Î D : x Î int(Sx) Ç int(S^–1x)} be the core of D. We know that D₀ is nonempty by the definition of effectiveness. Suppose first that y Î D₀. Since D Ì int(S^–1y) for every y Î D₀ (see [3], Proposition 2.2), there exists y Î S such that y = y(x). Also, there exists f Î S – {1} such that f(y) = y. By P_l we have fⁿy Î A, and fⁿy(x) = y, so that y Î S_Ax. For an arbitrary y take z Î D₀. We have seen that z Î S_Ax. We have to show that y Î cl(S_Az). Take f Î S – {1} such that f(z) = z and a sequence y_mÎ S such that y_m(z) ® y. By P_l, y_mfⁿÎ S_A for large enough n, and since y_mfⁿ(z) = y_m(z), there exists a sequence r_kÎ S_A with r_k(z) ® y.

As a consequence we have.

Corollary 1. Suppose that

satisfies both P_l and P_r. Then any effective control set for S is contained in a

-chain control set.

We can define effective -chain control sets.

Definition 3. Let be a family of subsets of S. A -chain control set is called effective if it contains an effective control set for S.

We observe that for a family satisfying both P_l and P_r a -chain control set E is effective if and only if the subset E₀ = {x Î E : x Î int(Sx) Ç int(S^–1x)} is not empty. In fact, if we assume that x Î int(Sx) Ç int(S^–1x) then there exists an effective control set D such that x Î D₀ (see [3], Proposition 2.3).

Let M be a compact metric space. Assume that S is a semigroup of homeomorphisms of M and suppose that d is a metric on M. In the group G of homeomorphisms of M we consider the metric of uniform convergence

which is right invariant under G. For a subset A Ì S we put

B(A, e) = {f Î G : $y Î A, d^¢(f, y) < e}.

We denote by S_e,A the subsemigroup of G generated by B(A, e).

We intend to show that points reachable by chains can be reached by the action of the perturbed semigroup S_e,A. For this it is required to consider the following assumption about the action of G on M.

Hypothesis H: There exist real numbers c > 0 and h > 0 satisfying the following property: for all x Î M and y Î B_h(x), there exists f Î G such that f(x) = y and d(f(x), x) > cd¢(f, 1_M).

In general this condition is not satisfied.

Example 1. Consider the compact metric space

where C_n are the circles C_n = {(x, y) Î ² : x² + y² = 1/n}, with the metric inherited from the standard metric of ². All homeomorphisms f of M have the property that f(0) = 0, and therefore the hypothesis H is not satisfied at 0. In fact, if f(0) ¹ 0 then the connected component containing f(0) is a circle. The connected component containing 0 is the set {0}. And clearly this set in not homeomorphic to a circle.

However, we observe that in [2] it was shown that hypothesis H holds for the action of a Lie group G on a large class of homogeneous spaces G/H, namely those for which there is a compact subgroup K Ì G which acts transitively on G/H. This class of homogeneous spaces includes the flag manifolds (Furstenberg boundaries) of semi-simple Lie groups G.

Now, we can relate (S, e, A)-chains with reachability of S_e,A.

Proposition 2. Take x,y Î M and A Ì S. Then

1. There exists an (S, e, A)-chain from x to y if y Î S_e,Ax. We also have that there is a (S, e^¢, A)-chain from x to y for every e^¢ > e if y Î cl(S_e,Ax).

2. Suppose that the hypothesis H is satisfied and take e such that 0 < e < h. Assume that x₀,¼, x_nÎ M and f₀,¼,f_n–1, determine a (S, e, A)-chain from x₀ to x_n. Then there exists y Î S_e¢,A such that y(x₀) = x_n, where e^¢ = e/c.

Proof. 1. Take y Î S_e,Ax. Then, there exists f Î S_e,A such that y = f(x). It follows from the definition of S_e,A that f = f_k–1¼f₀ with f_iÎ B(A, e), i = 0,¼, k – 1. We choose y₀,¼, y_k–1Î A with d¢(y_i, f_i) < e, i = 0.., k – 1. The sequences x₀, x₁ = f₀(x₀),¼, x_k = f_k–1(x_k–1) = y and y₀,¼, y_k–1 determine an (S, e, A)-chain from x to y. In fact,

for i = 0,¼, k – 1. Consequently there exists a (S, e, A)-chain from x to y. Now, suppose that y Î cl(S_e,Ax). There exists a sequence f_nÎ S_e,A such that f_n(x) converges to y. Take e^¢ > e and let n₀ be such that d((x), y) < e^¢ – e. As before, there exist a (S, e, A)-chain from x to (x). Let y₀ = x,¼, y_n = (x₀) Î M, y₀,¼, y_n–1Î A be a (S, e, A)-chain from x to (x). Thus d(y_i(y_i), y_i+1) < e for i = 0,¼, n – 1. Therefore, the chain z₀ = x, z₁ = y₁,¼, z_n–1 = y_n–1, z_n = y and y₀,¼, y_n–1Î A determine an (S, e, A)-chain from x to y. In fact,

and d(y_i–1(y_i–1), y_i) < e < e^¢ for i = 1,¼, n – 1.

2. Since d(f_i(x_i), x_i+1) < e < h, the hypothesis H implies that there is y_i Î G such that

i = 0,¼, n – 1, and therefore d¢(y_i, 1_M) < e/c = e^¢. Define t_i = y_if_i. We have

because d¢ is right invariant. Therefore, t_iÎ B(A, e^¢). On the other hand, t_i(x_i) = y_if_i(x_i) = x_i+1, and x_n = t_n–1¼t₀(x₀).

Proposition 3. Suppose that the hypothesis H is satisfied and assume that

satisfies P_l and P_r. Let D be an effective control set for S on M. Then, for each e > 0 and A Î there exists a control set D_e,A for the perturbed semigroup S_e,A such that D Ì D_e,A.

Proof. In fact, for x, y Î D, we will show that y Î S_e,Ax, for e small enough. By Proposition 1, there exists, f Î S_A such that f(x) is near y. On the other hand, by the definition of S_A we have f = f₁¼f_n with f_iÎ A. Using H, there is g with d¢(gf, f) = d¢(g, 1) < e and gf(x) = y so that gf Î S_e,A and y Î S_e,Ax.

The next theorem characterizes the -chain control sets as intersections of control sets for the perturbed semigroups.

Theorem 1. Let S be a semigroup of homeomorphisms of a compact metric space M. Suppose that the action of S on M satisfies H, and consider a family

of subsets of S satisfying P_l and P_r. Let D be an effective control set for S on M, and for e > 0 and A Î , denote by D_e,A the S_e,A control set containing D. Then

is the only -chain control set containing D.

Proof. Since D Ì E we have int(E) ¹ Æ. Also, for any x, y Î E, y Î cl(S_e¢,Ax) for all e¢ > 0 and A Î . Therefore, by the Proposition 2 there exists a (S, e, A)-chain from x to y for all e > 0 and A Î , which shows that E is chain transitive. It remains to verify the maximality of E. Take x Ï E and y Î E and suppose that for every e > 0 and A Î there are (S, e, A)-chains from x to y and from y to x. Since the action of S on M satisfies H and S_e,AÌ S_e¢,A for e^¢ > e, Proposition 2 shows that y Î S_e,Ax and x Î S_e,Ay for all e > 0 and A Î . However, y Î D_e,A, so that x Î D_e,A for all e, A contradicting the assumption that x Ï E. Hence, there is no chain either from x to y or from y to x, which shows the maximality of E.

Proposition 4. Let the assumptions be as in the previous theorem and suppose moreover that there is just one invariant control set, say D, for S in M. Then D _{e ,A} is the S _{e ,A}-invariant control set containing the invariant control set for S.

Proof. By [1, Lemma 3.1] there is only one closed invariant control set, say C, for S in a compact metric space M if and only if C = Ç_xÎM cl(Sx) ¹ Æ. Define C_e,A = Ç_xÎM cl(S_e,Ax). Thus, it is enough to show that D_e,AÇ C_e,A¹ Æ. Pick x Î M. Since D Ì int(S^–1y) for every y Î D₀ we can choose f Î S such that f(x) Î D₀. But satisfies property P_l and therefore fⁿ Î A for some integer n (take f = y in the definition of P_l). We have that fⁿ(x) Î D because D is invariant. Since D Ì D_e,A, and D_e,A is a control set for S_e,A it follows that D_e,A Ì cl(S_e,Ax).

3 Fiber bundles

In this section we study the behavior of -chain control sets on principal bundles and their associated bundles. We refer to [9] for the theory of fiber bundles.

We start by settling some notation. Let G be a topological group. Suppose that G acts effectively and on the right on a topological space Q. We denote by Q(M,G) the principal bundle with total space Q , base space M and structural group G. We denote by p_Q : Q ® M the canonical projection.

Let S_Q be a semigroup of homeomorphisms of Q commuting with the right action, i.e., Qf(q · a) = Qf(q) · a, a Î G if Qf Î S_Q. The semigroup S_Q induces a semigroup S_M of homeomorphisms of M. In fact, if y Î M and y = p_Q(q) we define an element Mf Î S_M as

Mf(y) = p_Q(Qf(q)),

if Qf Î S_Q.

Suppose that the structural group G acts on the left and transitively on the topological group F. We consider the fiber bundle associated to the principal bundle Q(M, G) with typical fiber F. This bundle is denoted by E(M, F, G, Q), or simply by E, the total space of the bundle. Since we will be interested in the study of chain control sets we assume, in the paper, that E, Q and M are metric spaces.

The elements of E are equivalence classes with respect to the relation on Q × F given by (q, v) ~ (qa, a^–1v), a Î G. We use the notation [q, v], q Î Q, v Î F for an element of E.

The canonical projection p_E : E ® M on the fiber bundle is defined as p_E([q, v]) = p_Q(q).

Let Qf be a homeomorphism of Q commuting with the right action of G. Then Qf induces the homeomorphism of E defined by Ef([q, v]) = [Qf(q), v]. Therefore the semigroup S_Q of homeomorphisms of Q induces a semigroup S_E of homeomorphisms of E and

S_E([q, v]) = [S_Q(q), v]

Given q Î Q we define the subset

Through the identification of the fiber over x with G via a Î G q · a Î 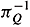(x), S_q can be viewed as a subset of G

It follows immediately that S_q is a subsemigroup of G if S_q ¹ Æ. We observe that S_q is the subsemigroup acting on the typical fiber.

The semigroups S_Q, S_E and S_q were also considered in [3].

Suppose that is a family of subsets of S_Q. The family induces a family _M in the semigroup S_M, a family _E in S_E and a family _q in S_q. In fact, for each A Î we define A_M = {Mf Î S_M : $Qf Î A and Mf(p_Q(q)) = p_Q(Qf(q))}, A_E = {Ef Î S_E : $Qf Î A and Ef([q, v]) = [Qf(q), v]} and A_q = {a Î G : $Qf Î A and Qf(q) = q · a}. Thus we can define the induced families _M = {A_M : A Î }, _E = {A_E : A Î } and _q = {A_q : A Î }.

Proposition 5. Let

be a family of subsets of S_Q satisfying both P_l and P_r. Then

_M,

_E and

_q also satisfy P_l and P_r.

Proof. In fact, take A Î . There exists n such that Qf(Qr)ⁿ = s Î A if Qf, Qr Î S_Q. Thus

and therefore Mf(Mr)ⁿÎ A_M. For the family _E we have

and Ef(Er)ⁿÎ A_E. Now, take a, b Î S_q and A_q Î _q. Then there exist Qf, Qy Î S_Q such that Qf(q) = q · a and Qy(q) = q · b. Thus Qf(Qy)ⁿ(q) = Qf(q·aⁿ) = q·baⁿ. Since Qf(Qy)ⁿÎ A we have baⁿ Î A_q. We argue in the same way for the P_r property.

The following theorem shows that chain control sets in the total space of a fiber bundle project into chain control sets in the base of the bundle.

Theorem 2. Let E be a fiber bundle with projection p : E ® M. Let

be a family of subsets in S_Q. Suppose that E is compact, and let H Ì E be a

_E-chain control set. Then there exists a

_M-chain control set B Ì M such that p(H) Ì B.

Proof. Since int(H) ¹ Æ and p is an open map, p(H) has nonempty interior. Take e > 0, A_M Î _M and x¢, y^¢ Î p(H). Pick x, y Î H such that p(x) = x¢ and p(y) = y¢. Let's show that there exists an (S_M, e, A_M))-chain from x¢ to y¢. Since E is compact, p is uniformly continuous so that there is d > 0 such that d(p(z), p(z¢)) < e if d(z, z¢) < d, z, z¢ Î E. Let x₀ = x, x₁,¼, x_n–1, x_n = y in E together with Ef₀, Ef₁,¼, Ef_n–1 in A_E form a (S_E, d, A_E)-chain from x to y. Since d(x_j, Ef_j(x_j)) < d we have that d(p(x_j), p(Ef_j(x_j))) = d(p(x_j), Mf_j(p(x_j))) < e which shows that p(x_i), Mf_i determine a (S_M, e, A_M))-chain from x^¢ to y^¢. Since p(H) satisfies properties 1 and 2 in the definition of a _M-chain control set it is contained in a _M-chain control set.

We recall that we are assuming that S_Q and have the accessibility property. However, since we wish to work over effective _M- chain control sets, the following version of accessibility is needed.

Definition 4. Let be a family of subsets of S_Q satisfying both P_l and P_r. Suppose that H is an effective _M-chain control set in M and take H₀ = {x Î H : x Î int(S_Mx) Ç int(x)}. The semigroup S_Q is said to be accessible over H₀ if for every q Î 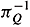(H₀), int(S_Qq) Ç 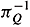(H₀) ¹ Æ.

Lemma 1. Let H Ì M be an effective

_M-chain control set and suppose that S_Q is accessible over H₀. Then int(S_q) ¹ Æ if q Î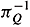 (H₀).

Proof. Take Qf Î S_Q such that Qf(q) Î int(S_Qq) Ç 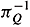(H₀). There exists an effective control set D for S_M such that x = p_Q(q) Î D₀. Thus p_Q(Qf(q)) = Mf(p_Q(q)) Î D₀ and there exists Qy Î S_Q such that My(p_Q(Qf(q))) = x, so that QyQf(q) belongs to the same fiber as q. Now, QyQf(q) Î int(S_Qq) hence if we let a Î G be such that QyQf(q) = q · a then a Î int(S_q) showing the lemma.

As a converse of Theorem 2, we have

Theorem 3. Let E be a fiber bundle with projection p : E ® M. Let

be a family of subsets in S_Q satisfying both P_l and P_r. Suppose that E is compact, B Ì M is an effective

_M-chain control set and that S_Q is accessible over B₀. Then there exists an effective

_E-chain control set H Ì E and such that p(H) Ì B.

Proof. Take x Î B₀ = {x Î B : x Î int(S_Mx) Ç int(x)} . Then x belongs to an effective control set C contained in B ([3, Proposition 2.3]). We have shown in [3, Proposition 3.4] that there exists an effective control set D Ì E for S_E with p(D) Ì C. Corollary 1 implies that D is contained in a _E-chain control set, say H. Using the fact that chain control sets do not overlap and the Theorem 2 there exists a _M-chain control set B Ì M satisfying p(E) Ì B.

Let d_E be a metric on the total space E of the fiber bundle with typical fiber F. Let also d_F be a right invariant metric on the fiber F. Consider a metric d_M on the base space M such that the canonical projection p_E : E ® M is Lipschitizian, that is, there exists a constant c > 0 such that for every x, y Î E we have d_E(x, y) < cd_M( p_E(x), p_E(y)).

The characterization of the chain control sets as intersection of control sets of the perturbed semigroup gives us the following result.

Theorem 4. Let E be an fiber bundle associated to the principal bundle Q whose structural group is compact. Suppose that M and E are compact and that Q is connected. Assume that

is a family of subsets of S_Q satisfying P_l and P_r. We also assume that the actions of the groups of homeomophisms on M and E satisfy the hypothesis H. Let B be an effective

_M-chain control set on M and suppose that S_Q is accessible over B₀. Then

(B) is an effective

_E-chain control set on E. Therefore there are as many effective

_E-chain control sets in E as

_M-chain control sets in M.

Proof. We first show that ((S_M)e,A_M)_EÌ (S_E)ce,A_E, that is, Ef Î (S_E)ce,A_E if Mf Î (S_M)e,A_M. It is enough to show that Ef Î B(A_E, ce) if Mf Î B(A_M, e). This is true because

By the Theorem 1 we have B = Ç_e,A_M De,A_M where De,A_M is a control set for (S_M)e,A_M. Thus p^–1(B) = Ç_e,A_M p^–1(De,A_M). Now, [3, Proposition 3.7 and Proposition 3.9] implies that p^–1(De,A_M) is a control set for ((S_M)e,A_M)_EÌ (S_E)ce,A_E and therefore p^–1(B) is a _E chain control set in E, again by the characterization of chain control sets as intersections of control sets.

The next theorem shows that a

_q-chain control set in a fiber of a bundle is contained in a -chain control set in the total space.

Theorem 5. Let E be the bundle associated to the principal bundle Q with projections p_E and p_Q, respectively. Suppose that

is a family of subsets of S_Q. Take q Î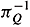 (x), x Î M. Assume that H is a

_q-chain control set on F. Then

1. Any

_q-chain control set in (x) is contained in a -chain control set in Q.

2. [q,H] is contained in a

_E-chain control set in E.

Proof.

1. Let H be a _q-chain control set in (x). Pick z, z^¢ Î H. Then for every e > 0 and A_q Î _q there exists x₀ = z, x₁,¼ > ,x_n–1, x_n = z^¢ in (x) and >a₀, a₁,¼, a_n–1Î A_q such that >d(x_ja_j, x_j+1) < e for j = 0,¼, n – 1. Let >Qf_j Î A be defined as Qf_j(q) = qa_j. Then >x₀,¼, x_n and Qf_j, j = 0,¼, n – 1 determine a >-chain from z to z^¢.

2. Take [q, v] and [q, v¢] in [q, H]. Since H is a _q-chain control set, for every e > 0 and A_q Î _q there exist v₀ = v,¼, v_n = v^¢ in F and a₀,¼, a_n–1Î A_q such that d_F(a_jv_j, v_j+1) < e for j = 0,¼, n – 1. Let Qf_jÎ A be defined as Qf_j(q) = qa_j. Then [q, v₀],¼,[q, v_n] and Ef_j, j = 0,¼, n – 1 determine a (S_E, e, A)-chain from [q, v] to [q, v¢]. In fact,

Remark. Since we can construct the invariant control sets in the total space of an associated bundle in terms of the invariant control sets in the fibers (see [3]) we could ask if this is also true for the chain control sets which contains the invariant control set. We have tried to answer this question using the characterization of chain control sets as intersections of control sets (Theorem 1). The proof does not work because the semigroup associated (in the fiber) of the perturbed semigroup in the total space does not coincide with the perturbed semigroup of the fiber and there is no useful inclusion between them. We observe that Theorem 5 can be regarded as a lemma in this expected description of the chain control sets in fiber bundles.

4 Acknowledgment

I would like to thank an anonymous referee for suggestions to improve the paper, in particular for providing Example 1.

Received: 19/IX/03.

Accepted: 30/IX/03.

#460/98.

• [1] L. Arnold, W. Kliemann and E. Oeljeklaus, Lyapunov, A exponents of linear stochastic systems in: Lyapunov Exponents, Arnold L. and Wihstutz V. (eds), LNM-Springer 1186 (1986), Berlin.
• [2] C.J. Braga Barros and L.A.B. San Martin, Chain control sets for semigroup actions Computational and Applied Mathematics, 15, 3 (1996), Birkhäuser, 257-276.
• [3] C.J. Braga Barros and L.A.B. San Martin, On the action of semigroups in fiber bundles Matemática Contemporânea, 13 (1997), Sociedade Brasileira de Matemática, 1-19.
• [4] F. Colonius and W. Kliemann, Linear control semigroups acting on projective spaces Journal of Dynamics and Differential Equations, 5, 3 (1993), 495-528.
• [5] F. Colonius and W. Kliemann, Some aspects of control systems as dynamical systems Journal of Dynamics and Differential Equations, 5, 3 (1993), 469-494.
• [6] F. Colonius and W. Kliemann, Remarks on ergodic theory of stochastic flows and control flows In Proceedings of the Conference on Stochastic Flows (Wihstutz V. ed.) Birkhäuser, Boston (1990).
• [7] F. Colonius and W. Kliemann, The dynamics of control Birkhäuser, Boston (2000).
• [8] F. Colonius, W. Kliemann and L.A.B. San Martin, Asymptotic problems - from control systems to semigroups Positivity in Lie Theory: Open Problems Walter de Gruyter GmbH & Co. Berlin - New York (1998).
• [9] D. Husemoller, Fibre Bundles Graduate texts in Mathematics 20. Springer Verlag, New York Heidelberg Berlin (1975).
• [10] S. Kobayashi and K. Nomizu, Foundations of differential geometry John Wiley & Sons, New York (1963).
• [11] L.A.B. San Martin and P.A. Tonelli, Semigroup actions on homogeneous spaces Semigroup Forum, 50 (1995), 59-88.
• [12] L.A.B. San Martin, Control sets and semigroups in semi-simple Lie groups In Semigroups in algebra, geometry and analysis. Gruyter Verlag, Berlin (1994).

*

Research partially supported by CAPES/PROCAD - Teoria de Lie e Aplicações, grant n. 00186/00-7.

Publication Dates

• Publication in this collection
  20 July 2004
• Date of issue
  2003

History

• Received
  19 Sept 2003
• Accepted
  30 Sept 2003