Photoproduction of excited baryons in the 1 /Nc expansion of QCD

TALK

Photoproduction of excited baryons in the 1 /N_c expansion of QCD

N. N. Scoccola^*

Physics Department, Comisión Nacional de Energía Atómica, (1429) Buenos Aires, Argentina, CONICET, Rivadavia 1917, (1033) Buenos Aires, Argentina, and Universidad Favaloro, Solís 453, (1078) Buenos Aires, Argentina

ABSTRACT

We present results for the photoproduction helicity amplitudes of excited baryons obtained in the context of the 1 /Nc expansion of QCD. The results show that, in order to get a satisfactory description of the observed photoproduction amplitudes, the sub-leading corrections in 1/Nc are important. We also find that, while one-body effective operators are dominant, there is some evidence for the need of two-body effects which, in general, are not included in quark model calculations.

Keywords: Excited baryon photoproduction; Large Nc QCD

1. INTRODUCTION

Baryon photo-couplings have been the subject of many studies over the last forty years, and are key elements in the understanding of baryon structure and dynamics. In this talk I will present the results of the photoproduction helicity amplitudes for excited baryons in the context of the 1/N_c expansion of QCD [1]. Such an expansion has been shown to provide a useful and systematic framework for the analysis of various baryon properties. This is mostly due to the existence of a contracted spin-flavor symmetry in the large N_c limit[2, 3]. Although SU (2Nf) is not an exact symmetry in the excited baryon sector[4], its breaking is small as several analyses of the baryon spectrum have shown[5-7]. In this context the photoproduction helicity amplitudes for the negative parity excited baryons have been first analyzed in [8]. Here we report on an extension of such analysis which includes a systematic building of a complete basis of current operators to sub-leading order in the 1/N_c expansion, for both negative and positive parity resonances[9, 10].

2. FORMALISM

The helicity amplitudes of interest are defined in the standard form[11]

where δ = 1/2 or 3/2 is the helicity defined along the -axis, which coincides with the photon momentum, is the photon's polarization vector for helicity + 1, a is the fine-structure constant, and N and B* denote respectively the initial nucleon and the excited baryon. A sign factor η(B*) from the strong amplitude for πN → B* is included. The electromagnetic current is represented as a linear combination of effective current operators which have the most general form where the upper scripts display the angular momentum and isospin, and throughout the neutral component, i.e. I₃ = 0, is taken.is an irreducible tensor built with the photon momentum, chosen here to be a spherical harmonic, and are operators where is the 0(3) tensor associated with the excited baryon state normalized by its reduced matrix element (RME) is a spin-flavor tensor operator with I = 0 or 1, which can be expressed in terms of products of the generators of SU (4) acting either on the excited quark,λ= s, t, g, or the N_c - 1 quark core,. We assume here that quark charges are N_c independent. Bases of effective operators B^[LI] can be obtained along similar steps to those followed, for instance, in the study of strong transitions[12, 13]. Since there is a one to one correspondence between L and the multipole to which an operator contributes to, we denote them accordingly, e.g., EL^S_n is the n^th EL isoscalar operator. The bases of operators are given in Table I for the negative parity multiplet [20',1-] in Table II for the Roper multiplet [20, 0+] and in Table III for the [20, 2+]-plet. Note that for the photoproduction of positive parity resonances we need only to consider the total SU(4) generators Λ =λ + Λ_c, and in the case of the [20, 0+]-plet we can simply replace ξ(=0) = 1. The numerical factors in front of each operator conveniently normalize the largest RME (see Eq.(2) below) to be equal to 1 (1/3) for operators 0(1) (O(1/Nc)) when Nc = 3. The E- and M-multipole components of a given helicity amplitude of isospin I can be expressed in terms of the RME of the operators B^[LI] as follows

where X = M (E) and w_X (L) = 1with = negative (positive). Here, π_ex is the parity of the excited multiplet. In Eq.(2) I₃ denotes the isospin projection of the initial nucleon. The factor results from taking transition matrix elements between excited and ground state baryons[14]. The RME in Eq.(2) can be evaluated using similar techniques to those in [5]. The coefficients are determined by fitting to the empirical helicity amplitudes[11]. Their co-dependencies are taken here to be the natural ones for the multipole transitions. The sign η(B*) can be fixed from the studies in [12, 13]. Those analyses determine the signs up to an overall sign for each pion partial wave. In the case of the Roper multiplet this does not bring in any ambiguity. Since the partial waves involved in the case of the [20', 1^—]-plet are S and D waves, we have one extra relative sign, which we will call ξ. In the case of the [20, 2+] the contributions come from the P and F waves and we will denote the extra sign ξ' = sign(P/F).

3. RESULTS AND THEIR ANALYSIS

In this section we present and analyze the different fits to the helicity amplitudes. The coefficients to be fitted are expressed by including the barrier penetration factor: , where L' = L — 1 for EL operators, L' = L for ML operators. Throughout we will choose the scale Γ = m_p. For each multiplet we have performed several leading order (LO) and next-to-leading order (NLO) fits.

3.1. Negative parity resonances

We start by the results for the [20', 1^—]-plet. For N_c = 3, the states contained in such multiplet are as follows: two N states with J* = 1/2, two with J* = 3/2 and one Δ with J* = 5/2, and one Δ with J* = 1/2 and one with J* = 3/2. There are two mixing angles, θ₁ for the pair of excited N states with J* = 1/2, and θ3 for the N pair with J* = 3/2. The mixing angles are defined in the standard fashion [5], and have been determined in different ways. In the 1 /N_c expansion in particular, they can be obtained from an analysis of the masses [5], and more precisely from analyzing strong transitions [12]. We use the latter in this work. Such analysis gives two consistent but different results for the mixing angle θ₃. The values (in radians) θ₃ = 2.82 and θ₃ = 2.38 cannot be distinguished from the strong fits. One finds that some of the η signs are different for these two values. We take into account this with an extra sign factor κ, which is equal to +1 ( — 1) for θ₃ = 2.82 (2.38). A first analysis concerns the choices left by the values of the mixing angle θ₃, and the signs ξ and κ. Using all the LO operators, the choices are made by considering the χ² for all possibilities. The sign ξ = —1 is strongly favored. This is in agreement with an old determination based on the single-quark-transition model [15, 16]. The second choice that is favored, although less markedly than the one for ξ is θ3 = 2.82. Finally, for κ there is no indication of a preference from the fits; for the sake a definiteness we will take κ = +1 in our fits. This latter sign basically depends on strong amplitudes which are small and have large relative errors, which imply that its determination is subject to a degree of uncertainty. The helicity amplitudes show here their importance by allowing to determine the relative sign ξ between the strong S and D wave amplitudes, and by selecting between the two possible values of θ₃ consistent with the strong transitions. Note that θ₃ = 2.82 corresponds to "small"mixing, while 2.32 corresponds to "large"mixing. A simultaneous fit of strong transitions and photoproduction amplitudes is the best way of extracting the mixing angles. This will be carried out in a future project.

The helicity amplitudes resulting from the fits we have carried out are displayed in Fig. 1; the corresponding fit coefficients are given in Table I. In the fits we expand the operator matrix elements in powers of 1/N_c to the order corresponding to the fit. In the LO fits, we have set the errors in the input helicity amplitudes to be equal to 0.3 of the value of the helicity amplitude or the experimental value if this is larger. The point of this is to test whether or not the LO analysis is consistent in the sense that it gives a χ² per degree of freedom (χ²d_of) close to unity. For the NLO fits, we use of course the empirical errors. We now proceed to discuss the results.

The LO fit shows a 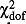of 2.42. This indicates that there are NLO effects to be taken into account for a satisfactory fit. The main deficiencies are in the fitting of the N( 1520) and the Δ(1620) amplitudes as one can readily ascertain from their individual contributions to the total χ². If one keeps only the LO operators with the largest coefficients (say coefficients bigger than 2), the 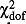does not change much from the one obtained with all LO operators. Notice that one 2-body LO operator seems to be significant, namely . We have checked that a fit taking κ = -1 leads to similar results except that the coefficient of results to be only 40% of the caseκ = +1. If indeed 2-body operators should give small effects, then this would be a way to discriminate about the sign κ. In fact, a LO fit using only 1-body operators gives respectively 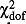= 2.48 and 2.12 for κ = +1 and -1.

One can perform a LO fit motivated by the single-quark-transition model [15, 16], which is also commonly used in quark model calculations. In that model, the photon only couples to the excited quark with a fixed ratio for the isoscalar versus the isovector coupling as given by the bare quark charges. Here this is achieved by locking 1-body operators as follows: , and . Note that the isoscalar counterpart of the last operator does not appear in the operator basis because it is spin-flavor singlet. The fit has at LO, which is similar to the result with unlocked operators, thus indicating that at LO one cannot draw a clear conclusion.

As it is well known, in the single-quark-transition model the so-called Moorhouse selection rule [17] holds. That rule states that the amplitudes for photoexcitation of protons to ⁴N* states vanish. In the present analysis, the rule is violated by the unlocking of the 1-body operators, and by 2-body operators. At the level of physical states, the rule tends to suppress the amplitudes pγ→N(1650), N(1700), and N(1675). In the first two cases, the mixing angles θ₁ and θ₃ work against that suppression as they give to these states a component ²N^*. In the case of N(1675), the rule turns out to be mostly violated by 2-body effects, at least for κ = +1.

The NLO order fit NLO1, involves all operators in the basis. It gives values for the coefficients of the LO operators which are, within the expected deviations from 1 /N_c counting, consistent with the values obtained in the LO fits. Moreover, none of the coefficients of the NLO operators has a magnitude larger than that of the largest LO coefficients. This is a strong indication of the consistency of the 1 /N_c expansion. We find that this consistency is more clearly manifested here than in the case of the positive parity baryons analyzed below. From the magnitude of the coefficients, it is obvious that only a few NLO operators are needed for a consistent fit. In fact, as shown by the fit NLO2 in Table I, a consistent fit is obtained with only five LO and one NLO operators. Of these dominant operators four are one-body and LO, and two are two-body with one of them LO and the other NLO. Note also that none of the 2-body E3 operators is required. It is remarkable that out of eleven NLO operators only one is essential for obtaining consistent fits. At this point it is important to mention that many of the empirical amplitudes have errors that are larger than what is needed for an accurate NLO analysis. It is for this reason that one cannot draw a more precise NLO picture which could unveil the role of other operators. To test for deviations from the single-quark-transition model at NLO, we have performed a NLO fit including all operators with locked the 1-body operators. The result is a 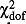~ 2.5, which gives a good indication that there are deviations from that model.

At this stage we can compare our analysis with that of Carlson and Carone [8]. We have checked that their set of operators, eleven in total, corresponds to a subset of our operator basis, which can be obtained by locking several pairs of operators using the isoscalar to isovector ratio of the electric charge operator as we explained earlier. In this case, 1- as well as 2-body operators are locked. A fit with that set of locked operators gives a 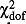~ 3.2. This result clearly indicates the necessity for the more general basis we use in this work. However, one should emphasize that the main features of most helicity amplitudes are obtained in the analysis of Ref. [8]. Another point where we differ from Ref. [8] is in the mixing angles: in our analysis we take the mixing angles from the strong decays, while in Ref. [8] some of the fits include fitting the mixing angles. Their mixing angles are somewhat different from ours, leaving an open issue which should be sorted out. We plan to carry out simultaneous fits of strong decays and helicity amplitudes, from where we expect to extract more reliable values for the mixing angles.

3.2. Positive parity resonances

We first discuss the helicity amplitudes of the Roper multiplet. The results of the fits are displayed in Table II and the corresponding amplitudes in Fig.2. At leading order (LO), only the isotriplet operator contributes, and the fit gives . The main problem is the small magnitude of the δ = 3/2 amplitude, especially because a 2-body operator is necessary to fit it. As seen from fit NLO, the operator is the one that brings agreement while the operators M1^S₁ and turn out to be less important as shown by the relative error of their coefficients. A definite conclusion requires, however, an improvement in the empirical values of the Δ(1600) amplitudes.

In the [20, 2⁺] multiplet, the helicity amplitudes associated with the N(1680) and Δ(1950) are well known, with the others less well established. The results of our fits for the choice ξ'= -1 are displayed in Table III and corresponding amplitudes in Fig.3. The main contribution to the χ² at LO is due to the large δ = 3/2 amplitude of the proton N(1680), which is badly underestimated. It should be noted that the choice ξ' = +1 leads to a qualitatively similar LO fit. The NLO analysis is somewhat limited by the large errors of the inputs, which exceed in general the 10% error that would allow for an accurate NLO analysis. The NLO1 fit shows that for ξ' = -1 the coefficientsneeded to reproduce the empirical amplitudes are all of natural magnitude, indicating a good convergence of the 1 /N_c expansion.

It also implies that a reduced number of operators give the significant contributions as shown by the relative errors of the coefficients. This is confirmed by the NLO2 fit where we have included the minimum number of operators that allow for a

~ 1. This is not the case for ξ' = +1 choice. It is important to note that a fit that keeps only 1B operators among the significant operators leads to a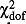 ~ 2, which is showing that the dominant effects result from the coupling of the photon to a single quark. Returning to the large δ = 3/2 amplitude of the N(1680), at NLO it receives several contributions. All of them have the same sign and none is dominating, which makes the understanding of the large magnitude of this amplitude difficult.

4. SUMMARY AND CONCLUSIONS

In this contribution I have reported on the 1 /Nc expansion analysis of baryon photoproduction helicity amplitudes of both negative and parity excited baryons. The most important outcome of the analysis is that the expected hierarchies implied by the 1 /Nc power counting are respected. Another important aspect is that, in general, only a reduced number of operators in the basis turn out to be relevant. Several of those operators can be easily identified with those in quark models, but there are also 2-body operators usually not included in quark models which are necessary for an accurate description of the empirical helicity amplitudes. In the case of the [20', 1^-] the present analysis allows one to select between the two possible values of the mixing angle 6₃ which are consistent with strong decays, as well as the relative sign £ between the S and D-wave strong amplitudes. A comprehensive analysis that includes strong and helicity amplitudes will further refine the results of this work, and is expected to be presented elsewhere. Our analysis also shows the dominance of M1 transitions in the amplitudes of the [20, 0+] excited baryons and of the M3 and E2 transitions in the [20, 2+] ones.

Acknowledgements

I am indebted to J. Goity and N. Matagne in collaboration with whom the work reported in this contribution has been done. I would also like to thank the organizers for their warm hospitality during the workshop. This work was supported by CONICET (Argentina) grant # PIP 6084 and by ANPCyT (Argentina) grant # PICT04 03-25374.

[1] G. 't Hooft, Nucl. Phys. B 72, 461 (1974); E. Witten, Nucl. Phys. B 160, 57 (1979).

[2] J.L. Gervais and B. Sakita, Phys. Rev. Lett. 52, 87 (1984) ; Phys. Rev. D 30, 1795 (1984).

[3] R. Dashen and A.V. Manohar, Phys. Lett. B 315, 425 (1993); Phys. Lett. B 315, 438 (1993); E. Jenkins, Phys. Lett. B 315, 441 (1993).

[4] J.L. Goity, Phys. Lett. B 414, 140 (1997).

[5] C. E. Carlson, C. D. Carone, J. L. Goity, and R. F. Lebed, Phys. Lett. B 438, 327 (1998); Phys. Rev. D 59, 114008 (1999).

[6] C. L. Schat, J. L. Goity, and N. N. Scoccola, Phys. Rev. Lett.88, 102002 (2002); Phys. Rev. D 66, 114014 (2002); Phys. Lett. B 564, 83 (2003) .

[7] N. Matagne and F. Stancu, Phys. Rev. D 71, 014010 (2005); Phys. Lett. B 631, 7 (2005); Phys. Rev. D 73, 114025 (2006).

[8] C. E. Carlson and C. D. Carone, Phys. Rev. D 58, 053005 (1998).

[9] J. L. Goity and N. N. Scoccola, Phys. Rev. Lett. 99, 062002 (2007)

[10] N. N. Scoccola, J. L. Goity, and N. Matagne, Phys. Lett. B 663, 222 (2008)

[11] Particle Data Group, W.-M. Yao et al., J. Phys. G33, 1 (2006).

[12] J. L. Goity, C. L. Schat, and N. N. Scoccola, Phys. Rev. D 71, 034016 (2005).

[13] J. L. Goity and N. N. Scoccola, Phys. Rev. D 72, 034024 (2005).

[14] J. L. Goity, Phys. Atom. Nucl. 68, 624 (2005) [Yad. Fiz. 68, 655 (2005)] .

[15] F. J. Gilman and I. Karliner, Phys. Rev. D 10, 2194 (1974); A. J. O. Hey and J. Weyers, Phys. Lett. B 48, 69 (1974)

[16] J. Babcock and J. L. Rosner, Ann. Phys. 96, 191 (1976); J. Bab-cock, J. L. Rosner, R. J. Cashmore, and A. J. O. Hey, Nucl. Phys. B 126, 87 (1977).

[17] R. O. Moorhouse, Phys. Rev. Lett. 16, 772 (1966); F. E. Close, An introduction to quarks and partons, (Academic Press, London, 1979).

[18] R. Koniuk and N. Isgur, Phys. Rev. D 21, 1868 (1980)

(Received on 16 April, 2008)

Publication Dates

• Publication in this collection
  18 Nov 2008
• Date of issue
  Sept 2008

History

• Accepted
  16 Apr 2008
• Received
  16 Apr 2008