Abstract
A double barrier resonant tunneling device in which the well is made of a semi-magnetic material can work as an efficient spin filter. Today it is possible to make semiconductors that are ferromagnetic at room temperature. Therefore the device studied here has a great potential to be used as a polarizer, an analyzer and other spintronic applications. We discuss here the case of a Ga1-xMn xAs/Ga1-yAl yAs system because it can be integrated into the well known AlGaAs/GaAs technology. Our tight-binding Hamiltonian includes the kinetic energy, the double-barrier profile, the electric field, the magnetic term, the hole-impurity and the hole-hole interactions. The profile and the charge distribution are calculated self-consistently. In previous works we studied this system by solving the Hamiltonian in the reciprocal space, in order to simplify the treatment of the Poisson equation for the charge distribution. Here we introduce a simple one dimensional Green function that permits to solve all terms in the real space. Besides, a real space renormalization formalism is used to calculate exactly the electronic currents for each spin polarization. The results confirm that the proposed system is a good device for spintronics.
Transport properties; Double barrier spin filter; Tight-binding Hamiltonian
SPINTRONICS
A selfconsistent calculation of the transport properties of a double barrier spin filter
S. S. MaklerI; C. F. RitterI; I. C. da Cunha LimaII
IInst. de Física, Univ. Fed. Fluminense, Av. Gal. M. T. de Souza s/n, 24210-340, Niterói, RJ, Brazil
IIInst. de Física, Univ. do Estado de Rio de Janeiro, Rua S. F. Xavier 524, 20550-013, Rio de Janeiro, Brazil
ABSTRACT
A double barrier resonant tunneling device in which the well is made of a semi-magnetic material can work as an efficient spin filter. Today it is possible to make semiconductors that are ferromagnetic at room temperature. Therefore the device studied here has a great potential to be used as a polarizer, an analyzer and other spintronic applications. We discuss here the case of a Ga1-xMnxAs/Ga1-yAlyAs system because it can be integrated into the well known AlGaAs/GaAs technology. Our tight-binding Hamiltonian includes the kinetic energy, the double-barrier profile, the electric field, the magnetic term, the hole-impurity and the hole-hole interactions. The profile and the charge distribution are calculated self-consistently. In previous works we studied this system by solving the Hamiltonian in the reciprocal space, in order to simplify the treatment of the Poisson equation for the charge distribution. Here we introduce a simple one dimensional Green function that permits to solve all terms in the real space. Besides, a real space renormalization formalism is used to calculate exactly the electronic currents for each spin polarization. The results confirm that the proposed system is a good device for spintronics.
Keywords: Transport properties; Double barrier spin filter; Tight-binding Hamiltonian
I. INTRODUCTION
In the last years were developed diluted magnetic semiconductors (DMS), such as Ga1-xMnxAs [1,2] that are easily integrated in the AlGaAs/GaAs heterostructures technology. Today many electronic and opto-electronic devices such as leads, lasers are industrially produced using this technology. Besides, some semiconductors are ferromagnetic at room temperature [3-6].
Heterostructures using DMS can be tailored in order to make spintronic devices [7-10], such as spin polarizers and analyzers, spin valves and spin filters. By manipulating the electron spin degree of freedom we can produce smaller and faster processors and perhaps elements for quantum computing.
The device presented here was studied using Ga1-xMnxAs due to its potential applications. However, it is easy to extend our results for a variety of different DMS. It is important to search for devices operating at high temperatures, and in the absence of an external magnetic field. Homogeneous samples of Ga1-xMnxAs alloys with x up to 10% have been produced by molecular beam epitaxy at low temperatures, avoiding the formation of MnAs clusters [1,2]. In Ga1-xMnxAs the Mn2+ cations have the 3d shell partially filled with five electrons, in such a way that they carry a spin of S = 
 . In addition, the Mn ion binds a hole to satisfy charge neutrality. This kind of DMS introduces an interesting problem from the physical point of view: Mn in the alloy is a strong p dopant, the free hole concentration reaching even p = 1020-21cm-3. At small Mn concentrations, the alloy is a paramagnetic insulator. As x increases, it becomes ferromagnetic, going through a non-metal/metal transition for higher concentrations (x » 0.03) and keeping its ferromagnetic phase. For x above 5%, the alloy becomes a ferromagnetic insulator. In the metallic phase, the ferromagnetic transition is observed in the range of 30 - 110K, depending on the value of x. In samples of Ga1-xMnxAs with selective p-doping [11] it was reported a Curie temperature Tc ~ 172K.
. In addition, the Mn ion binds a hole to satisfy charge neutrality. This kind of DMS introduces an interesting problem from the physical point of view: Mn in the alloy is a strong p dopant, the free hole concentration reaching even p = 1020-21cm-3. At small Mn concentrations, the alloy is a paramagnetic insulator. As x increases, it becomes ferromagnetic, going through a non-metal/metal transition for higher concentrations (x » 0.03) and keeping its ferromagnetic phase. For x above 5%, the alloy becomes a ferromagnetic insulator. In the metallic phase, the ferromagnetic transition is observed in the range of 30 - 110K, depending on the value of x. In samples of Ga1-xMnxAs with selective p-doping [11] it was reported a Curie temperature Tc ~ 172K.
II. THE HAMILTONIAN
We consider a double barrier heterostructure made of Ga1-yAlyAs in the middle of which lies a Ga1-xMnxAs quantum well in its metallic ferromagnetic phase.
As in previous works [12-14], the system is described by a tight-binding Hamiltonian
In those works the emitter and the collector had an aluminium content in order to rise the left and right Fermi levels above the fermi level of the well. This was done to prevent the holes to escape the well. As holes mediates ferromagnetism that could modify strongly the properties of the device. In this work we consider that the holes that escapes the well remain close tho the barriers due to the electrostatic attraction. The results of the present article confirm this assumption.
In expression (1)
K is the kinetic energy and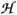 P describes the double-barrier profile. The term
P describes the double-barrier profile. The term 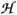 E, which represents the potential energy due to the applied bias, together with
E, which represents the potential energy due to the applied bias, together with 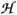 h-i and
h-i and 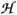 h-h, that take into account the interaction of the carriers with the potentials generated by the negative Mn impurities and the holes itself are calculated self-consistently. The potentials generated by the impurity and hole distributions are calculated by solving the Poisson equation,
h-h, that take into account the interaction of the carriers with the potentials generated by the negative Mn impurities and the holes itself are calculated self-consistently. The potentials generated by the impurity and hole distributions are calculated by solving the Poisson equation,
where r = ri + rh includes both the impurity and hole contributions. This potential gives a contribution
As the Hamiltonian is modified by this term so are modified its wave functions, from which the hole charge density rh is calculated.
Usually equation (2) is solved in the momentum space because it becomes an algebraic equation. On the other side, to solve the Hamiltonian (1) in the reciprocal space requires a big computational effort. In the context of a tight-binding calculation it is natural to express the Poisson equation in a finite difference formalism, in which it turns out to be a simple N × N matricial equation,
where a is the distance between layers. The inverse operator of the discretized one-dimensional Laplacian (its Green function) is obtained easily as
and it is symmetric. Using this Green function it is easy to obtain the potential as
Let us discuss now the mean field approximation used for the magnetic term. The hole interaction with the magnetic impurities is described through the contact potential,
where I is the p - d exchange coupling constant, Ri denotes the positions of the Ni impurities of Mn, S(Ri) is the (classical) spin of the impurity, and s(r) is the spin of the hole. We assume the layer in its metallic and ferromagnetic phase. Thus, the spin of the hole is well defined in that direction, being polarized either up (parallel) or down (anti-parallel). In order to write the magnetic term in the new basis we have to integrate over r. To do that, the magnetic impurities are assumed to be uniformly distributed in the Ga1-xMnxAs DMS layer, having the same magnetization < M > .
Therefore, a net Mn++ magnetization < M > polarizes the hole gas by introducing an additional effective confining potential given by
for z inside the well. Here s = ±1 for the hole spin and N0b = I/v0.
III. THE SPIN POLARIZED CURRENTS
We are dealing here with an open system, but the Hamiltonian given by equation (1) is first solved in a finite region including the double barrier and a small part of the contacts where the band bending, due to charge accumulation, occurs. This region can be seen in Fig. 1. Outside this region the profile is flat. Therefore the solutions are plane waves for energies above the Fermi level and evanescent modes below it. The total Hamiltonian can be written as 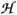 =
= 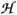 0 +
0 + 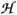 1, where
1, where 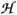 0 =
0 = 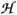 L +
L + 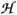 S+
S+ 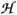 R describes the uncoupled regions corresponding to the left contact, the scattering region and the right contact, respectively. Thus each part of
R describes the uncoupled regions corresponding to the left contact, the scattering region and the right contact, respectively. Thus each part of 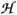 0 can be diagonalized exactly. We shall connect the three regions depicted in Fig.2 to get the exact solution for the open system. This method is the extension of the standard procedure described in elementary quantum text books, to the tight binding formalism.
0 can be diagonalized exactly. We shall connect the three regions depicted in Fig.2 to get the exact solution for the open system. This method is the extension of the standard procedure described in elementary quantum text books, to the tight binding formalism.
To relate the plane wave amplitudes on right and left of the double barrier we reconnect the three regions using the Hamiltonian
where v is the hopping that gives the effective mass m*. Here the left region goes from -¥ to -1, the N sites from 0 to N - 1 belong to the scattering region and labels from N to ¥ correspond to the right region. By labeling m = 0,...,N - 1 the eigenstates inside the scattering region, that come out from the numerical diagonalization of 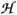 S, we can represent the reconnected regions by the diagram of Fig. 3.
S, we can represent the reconnected regions by the diagram of Fig. 3.
Here  = á
= á |
|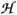 1|mñ = vá
1|mñ = vá |mñ are the hoppings from the left contact to the levels of the scattering region. In similar way we get vm1 = vám|1ñ. It easy to see that ám|1ñ = uNm, i. e., the last component of the m-th eigenvector.
|mñ are the hoppings from the left contact to the levels of the scattering region. In similar way we get vm1 = vám|1ñ. It easy to see that ám|1ñ = uNm, i. e., the last component of the m-th eigenvector.
Now it is easy to decimate all the states in the well. The result is a renormalization of the energies at sites -1 and N and the effective hopping between them. We get
where we denote the site -1 as  to simplify the notation. After that, to obtain the transmittance and therefore the current, is direct.
to simplify the notation. After that, to obtain the transmittance and therefore the current, is direct.
We emphasize that this procedure is non-perturbative. Thus the results are exact. The diagram representing the renormalized equations is shown in Fig. 4, where we have renamed the layers from N to ¥ as 1,2,...,¥
Now the solutions at the emitter (layers  and
and  ) can be easily connected with the solutions at the collector (Layers 1 and 2) to obtain the transmittance. Finally we get the current using the Landauer-Bütiker formalism.
) can be easily connected with the solutions at the collector (Layers 1 and 2) to obtain the transmittance. Finally we get the current using the Landauer-Bütiker formalism.
IV. RESULTS
We describe here a device in which the contacts are made of GaAs, the barriers of AlAs and the well of MnxGa1-xAs with x » 0.05 that correspond to a hole concentration p = 1020cm-3. The calculation is made at T = 0. Only heavy holes are considered here.
Due to the very high hole density inside the well, a simple iterative procedure to get selfconsistency does not converge. Instead, a quasi-Newton procedure for solving non-linear systems is used. It requires to diagonalize
S many times for each applied potential. However the diagonalization of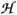 S is very fast because it is a finite tridiagonal matrix.
S is very fast because it is a finite tridiagonal matrix.
After this process, the selfconsistent profile and the spin polarized levels shown in Fig. 1 are obtained. Through the procedure described in the previous section we get the electronic current as a function of the applied bias shown in Fig. 5.
When a bias is applied, it is easy to see that the three polarized levels above the Fermi in Fig.1 begin to descend. When one of these levels is in between the Fermi level and the bottom of the band a current peak appear.
V. CONCLUSIONS
Using a decimation technique in a tight binding model we obtained the transmission probability and the current as a function of the bias. The strong spin-polarization inside the quantum well gives rise to a separation of the resonant peaks for each spin polarization of the order of 0.15eV, providing an excellent diode for applications in spin filtering [15-19].
As discussed in previous works [12-14] the device described here produces a current strongly polarized. Without taken into account the Rashba effect, the polarization is almost total. The only spin mixture is due to the very small tail of a -s transmittance peak at the central region of a s peak.
In a previous work [20] the peaks were not completely polarized because we considered the Rashba effect at the well walls that flip the spin of the carriers. Nevertheless this effect is quadratic in the small Rashba parameter a. Therefore the depolarization is small.
We conclude that a double-barrier heterostructure with a diluted ferromagnetic semiconductor at the well can be a very effective spin polarizer. Other effects, such as the disordered distribution of magnetic impurities have to be studied to confirm this prediction.
Acknowledgments
We thank FAPERJ and CNPq for financial support.
Received on 4 April, 2005
- [1] R. Fiederling, M. Keim, G. Reuscher, W. Ossau, G. Schmidt, A. Waag, and L. W. Molenkamp, Nature 402, 787 (1999).
- [2] Y. Ohno, D. K. Young, B. Beschoten, F. Matsukura, H. Ohno, and D. D. Awschalom, Nature 402, 790 (1999).
- [3] Y. Matsumoto, M. Murakami, T. Shono, T. Hasegawa, T. Fukumura, M. Kawasaki, P. Ahmet, T. Chikyow, S. Koshihara, and H. Koinuma, Science 291, 854 (2001).
- [4] Y. Matsumoto, Science 294, 1003 (2001).
- [5] K. Ueda, H. Tabata, and T. Kawai, Appl. Phys. Lett. 79, 988 (2001).
- [6] G. T. Thaler, M. E. Overberg, B. Gila, R. Frazier, C. R. Abernathy, S. J. Pearton, J. L. Lee, S. Y. Lee, Y. D. Park, Z. G. Khim, J. Kim, and F. Ren, Appl. Phys. Lett. 80 (21): 3964 (2002).
- [7] G. A. Prinz, Phys. Today (Apr 1995) 58.
- [8] J. Gregg et al, J. Magn. Magn. Mater. 175, 1 (1997).
- [9] S. Das Sarma, J. Fabian, X. Hu, and I. Zutic, Solid State Commun. 119, 207 (2001).
- [10] M. Oestreich, Nature 402, 735 (1999).
- [11] A. M. Nazmul, S. Kobayashi, S. Sugahara, and M. Tanaka, Physica E 21, 937 (2004).
- [12] S. S. Makler, M. A. Boselli, J. Weberszpil, X. F. Wang, and I. C. da Cunha Lima, Physica B 320, 396 (2002).
- [13] L. L. da Silva, M. A. Boselli, X.-F. Wang, J. Weberszpil, S. S. Makler, and I. C. da Cunha Lima, Braz. J. Phys. 32 433 (2002).
- [14] S. S. Makler, M. A. Boselli, and I. C. da Cunha Lima, proceedings of the 26th International Conference on the Physics of Semiconductors (ICPS-26) Edimburgh - UK, P152 (2002).
- [15] J. C. Egues, Phys. Rev. Lett. 80, 4578 (1998).
- [16] J. C. Egues and J. W. Wilkins, Phys. Rev. B 58, R16 012 (1998).
- [17] P. Bruno and J. Wunderlich, J. Appl. Phys. 84, 978 (1998).
- [18] V. A. Chitta, M. Z. Maiale, S. A. Leăo, and M. A. Degani, Appl. Phys. Lett. 74 2845 (1999).
- [19] E. A. de Andrada e Silva and G. C. La Rocca, Braz. J. Phys. 29, 719 (1999).
- [20] S. S. Makler, J. G. Zelcovit, M. A. Boselli, and I. C. da Cunha Lima, Physica B 354, 348 (2004).
Publication Dates
-
Publication in this collection
06 July 2006 -
Date of issue
June 2006
History
-
Received
04 Apr 2005
















