Electronic transport through a single-wall carbon nanotube with a magnetic impurity

NANOSTRUCTURES

Electronic transport through a single-wall carbon nanotube with a magnetic impurity

T. Lobo^I; M. S. Figueira^I; M. S. Ferreira^II

^IDepartamento de Física, Universidade Federal Fluminense Av. Litorânea s/n, 24210-346 Niterói-RJ, Brazil

^IIPhysics Department, Trinity College, Dublin 2, Ireland

ABSTRACT

We are interested in studying the transport properties of metallic single-wall carbon nanotubes (SWCNTs) with isolated magnetic impurities. We consider a metallic zigzag SWCNT in the form of an infinitely long cylinder of diameter D, connected by two metallic electrodes under a bias voltage $E$, with a magnetic impurity located on its surface. To describe the Kondo resonance we employ an impurity version of the atomic model, previously developed to study the Kondo insulator properties in the lattice case. We calculate the approximate Green's functions of the impurity Anderson model by employing the exact solution of the atomic limit of the Anderson model, where we use the completeness condition to choose the position of the chemical potential. We consider the SWCNT Green's functions in a tight-binding approach. We calculate density of states curves that characterize well the structure of the Kondo peak and we also present the dependence of the conductance with the diameter of the SWCNT.

Keywords: Transport properties; Single-wall carbon nanotubes; Magnetic impurities

I. THE ZIGZAG SINGLE-WALL CARBON NANOTUBE

A single-wall carbon nanotube (SWCNT) can be described as a graphene sheet rolled into a cylindrical shape so that the structure is one-dimensional with axial symmetry. Depending on their chirality, that can be expressed by the real space unit vectors and of the hexagonal lattice, the SWCNT vary from being metallic ( see Fig. 2) to semi-conducting (see Fig. 3). In this paper we are interested in studying zigzag SWCNT's that correspond to the chiral vectors (n, 0), where n is an integer proportional to the diameter D of the nanotube [1]. The zigzag SWCNT is always metallic when n is a multiple of 3 and the energy dispersion relation (k) for the zigzag nanotube can be written as [1]

with (-< ka < ), (q = 1,..., 2n) , where and the hopping energy between the carbon atoms of the nanotube, g₀, is considered as » 2.7 eV.

II. CONDUCTANCE OF A ZIGZAG SWCNT

The Kondo effect explains the enhancement of the low-temperature resistivity shown by a metal with magnetic impurities at low temperatures. The Kondo effect was experimentally detected in quantum dots [2] and in carbon nanotube devices [3]. These systems can be modeled by the Anderson impurity model and in this paper we employ an impurity version of the atomic model, previously applied to study the Kondo insulators [8], to describe the electronic transport properties of zigzag SWCNT's. In Fig. 1 we represent a pictorial view of the zigzag SWCNT with an impurity laterally attached [4]. At low temperatures and bias voltage, electron transport is coherent and a linear-response conductance is given by the Landauer-type formula [5]

where n_F is the Fermi function and S(w) is the transmission probability of an electron with energy w. This probability is given by S(w) = G² | |², where G corresponds to the coupling strength of the site 0 of the SWCNT conduction band to the impurity, here represented by the site 1, which is proportional to the kinetic energy of the electrons in the zigzag SWCNT. The Green function can be rewritten in terms of the exact Green function of the impurity, , calculated by the Dyson equation with V = |0ñ V á1| + |1ñ V á0| being the hybridization. The dressed Green's functions at the site 0 can be written in terms of the undressed Green's functions localized at the impurity, g₁₁, and the undressed Green's functions of the conduction band, g₀₀

Solving the equation system above and considering g₁₀ = 0 and g₀₁ = 0, we can write

where is given by [1]

and k_x obeys the relation

and

where (z) is calculated in Sec. IV.

III. THE ANDERSON IMPURITY MODEL

The Hamiltonian for the Anderson impurity with infinite Coulomb repulsion U is given by

where the first term represents the conduction electrons (c-electrons), the second describes the Anderson impurity characterized by a localized f level E_f,s, (we employ the f letter to indicate localized electrons at the impurity site) and the last one corresponds to the interaction between the c-electrons and the impurity. For simplicity we consider a constant hybridization V. We employ the Hubbard operators [6] to project out the double occupation state |f,2ñ, from the local states on the impurity. The identity decomposition in the reduced space of local states at the impurity is given by X_f,00 + X_f,ss + = I, where = -s, and the three X_f,aa are the projectors into the states |f,añ. The occupation numbers on the impurity n_f,a = < X_f,aa > should then satisfy the "completeness" relation

IV. THE ATOMIC MODEL

To obtain the exact f Green function G_ff,s(j_i, z) in real space for the impurity at site j_i, one can follow a procedure similar to the one used in [7] within the chain approximation, but considering all the possible cumulants in the expansion as it was done in [8] for the Anderson lattice. As with the Feynmann diagrams, one can rearrange all those that contribute to the exact G_ff,s(j_i, z) by defining an effective cumulant (j_i, z), that is given by all the diagrams of G_ff,s(j_i, z) that can not be separated by cutting a single edge (usually called proper or irreducible diagrams). We shall consider that the impurity is at the origin, and drop the index j_i from all the quantities. The exact GF G_ff,s(z) is then given by replacing the bare cumulant (z) = -/(z - e_f), where = << X_f,00 + X_f,ss >> _o, by the effective cumulant (z) at all the filled vertices of the chain diagrams in [7].The exact GF for the f electron is then written as

where (k,z) = -1/(z - e(k)). The exact atomic f Green function has the same form of Eq. (11), and it is calculated exactly in the ^{Appendix A} (cf. Eq. 13), and we write

From this equation we then obtain an explicit expression for (z) in terms of (z). To decrease the contribution of the c electrons, whose effect was overestimated by concentrating them at a single energy level we shall replace V² by D², with D = pV²/W is of the order of the Kondo peak's width, where W is related to the nanotube hopping energy by W = 6g_o. The atomic approximation consists in substituting (z) in Eq. (11) by the approximate (z) given by Eq. (12). As (z) is k independent, we can easily obtain the local Green function for the Anderson impurity for the zigzag nanotube, which is given by Eq. (11) but with (k,z) given by Eq. (6) and in the same way we obtain the conduction (G_c) and mixed (G_fc) Green's functions. One still has to decide what value of E₀ should be taken. As the most important region of the conduction electrons is the Fermi energy, we shall use E₀ = µ - dE₀, leaving the freedom of small changes dE₀ to adjust the results in such way that the completeness relation given by Eq. (10) should be satisfied.

V. RESULTS AND CONCLUSIONS

In Fig. 4 we plot the evolution of the density of states corresponding to a Kondo situation for three representative n values. We can see the two structures characteristic of the Kondo densities of states. One non-resonant peak located at the E_f position and the Kondo peak located at the chemical potential µ = 0. In the insets we represent details of each structure.

In Fig. 5 we represent the conductance of a side-coupled impurity in the zigzag nanotube. The Kondo effect depends on the diameter of the SWCNT and change the conductance of the system. The conductance varies more than two orders of magnitude as the nanotube diameter parameter n increases. At the same time, the Kondo peak becomes more steep, indicating that the Kondo temperature decreases as can be seen in the right inset of Fig. 4.

Received on 4 April, 2005

where W is the thermodynamical potential and the poles of the Green's functions are given by

where the residues are

where D = , D¢ = , tan f = and tan l = .

• [1] R. Saito, G. Dresselhaus, and M. S. Dresselhaus, Physical Properties of Carbon Nanotubes, Imperial College Press, (1999).
• [2] D. Goldhaber-Gordon, Hadas Shtrikman, D. Mahalu, David Abusch-Magder, U. Meirav, and M. A. Kastner, Nature 391, 156 (1998).
• [3] Jesper Nygard, David Henry Cobden, and Paul Erik Lindelof, Nature 408, 342 (2000).
• [4] R. Franco, M. S. Figueira, and E. V. Anda, Phys. Rev. B 67, 155301 (2003).
• [5] K. C. Kang, S. Y. Cho, J. J. Kim, and S. C. Shin, Phys. Rev. B. 63, 113304 (2001).
• [6] M. S. Figueira, M. E. Foglio, and G. G. Martinez, Phys. Rev. B 50, 17933 (1994).
• [7] R. Franco, M. S. Figueira, and M. E. Foglio, Phys. Rev. B 66, 45112 (2002).
• [8] M. E. Foglio and M. S. Figueira, Phys. Rev. B 60, 11361 (1999).

Appendix A:  Atomic solution

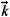state of the conduction band and one localized

We assume the zero conduction bandwidth W = 0. Therefore we eliminate from the Hamiltonian the hoping contributions. This corresponds to consider the relationship between a given 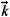state of the conduction band and one localized f state. In this case the analytical solution of the Hamiltonian is known [8]. The f atomic Green function is given by

Publication Dates

• Publication in this collection
  06 July 2006
• Date of issue
  June 2006

History

• Received
  04 Apr 2005