Controlling nonholonomic Chaplygin systems

Controlling nonholonomic Chaplygin systems

Antonio Carlos Baptista Antunes^I,*; Cássio Sigaud^I,†; Pedro Claudio Guaranho de Moraes^II,‡

^IDeptamento Física Matemática, Instituto de Física, Universidade Federal do Rio de Janeiro, Caixa Postal 68.528, 21.941-972 Rio de Janeiro RJ, Brasil

^IIDepartamento de Engenharia de Biossistemas, Universidade Federal de São João del-Rei, 36.301-160 São João del-Rei MG, Brasil

ABSTRACT

In this paper we deal with the problem of controlling some Chaplygin systems in the framework of the vakonomic approach for nonholonomic systems. Equations of motion for these systems are obtained which contain a free parameter that permits to control the system. It is show that given a prescribed path it is possible to determine the parameter of control which inserted in the equations of motion compel the trajectory of the system to follow the input function.

Keywords: Nonholonomic systems; vakonomic approach; Chaplygin systems.

1. INTRODUCTION

The subject of nonholonomic systems has a long history since the observation by Hertz that some types of mechanical systems subjected to nonintegrable constraints cannot be analysed in the framework of the lagrangian mechanics [1]. This means that the lagrangian formulation of mechanics does not give the correct equations of motion for these systems. The problem introduced by the so called nonholonomic constraints was circunvented by the introduction of the method of the lagrangian multipliers in lagrangian mechanics [2–4]. Since that times, nonholonomic systems are analysed on the basis of the Lagrange-d'Alambert principle and some others equivalent approaches [5].

More recently, it was observed that the nonholonomic contraints are an open window to the possibility of controlling nonholonomic systems. The Lagrange multiplier method conjugated with an adequate variational procedure gives a set of equations of motion which contain free parameters that can be used to compel the system to follow a prescribed path. This formulation, the so called variational axiomatic kind for nonholonomic systems or shortly vakonomic approach for nonholonomic system [6], is the procedure used in this paper to obtain the equations of motion of an instructive example, the Chaplygin sleigh [7], which is very convenient to shed some light on the details of the controlling mechanisms.

The general problem of the nonholonomic scleronomous systems consists in given a lagrangian L(q,) and a set of constraint equations,

to seek for the correct equations that describe the autonomous motion of the system, can be approached by the Lagrange-d'Alembert principle.

On the other hand, if we intend to obtain the equations of motion for a prescritive mechanics which admits the possibility of controlling the system, according to the vakonomic approach, the lagrangian must be extended to include the nonholonomic constraint conditions,

where λ_l(l = 1,...,m) are the Lagrange multipliers.

The Hamiltonian principle,

where L^' is the constrained lagrangian, gives the equations of the motion,

which are explicitly,

together with the constraint equations,

Using these n+m equations, it is possible to determine the _l(l = 1,...,m), which are the forces of the constraints on the system. The remaining λ_l are free parameters which can be conveniently chosen in order to force the system to follow a prescribed path in the coordinate space.

Our aim is to use a simple model, the Chaplygin sleigh to enlighten the procedure of determining the free parameters of control λ_l, which drive the system along a chosen curve given by a function on the horizontal plane.

2. THE MODEL

The vakonomic approach to nonholonomic systems summarized in the preceding section is applied to the Chaplygin sleigh. This apparatus consists of an eliptical board moving on a horizontal plane supported by two sliding points and a knife edge rigidly fixed under the board along the longitudinal axis. The contact point of the knife with the horizontal plane is at a distance a of the center of mass of the system. The coordinates used to describe the motion of this system are (x,y), the coordinates of the point of contact of the knife with the plane, Φ the angle between the knife (and the longitudinal axis of the board) and the x axis on the plane.

Let be the velocity of the point of contact of the knife. Its cartesian components are,

The equation for the constraint condition on the system is,

Let m be the mass of the sleigh and I the moment of inertia of the board and the knife around a vertical axis passing through the center of mass. The kinetic energy of the system is,

Following the vakonomic prescriptions described above, we write the extended lagrangian,

or

where,

is the radius of gyration of the system and

The equations (4) are used to obtain the equations of motion of the Chaplygin sleigh. In this way, we obtain the equations of the motion of the system,

Together with the equation that gives the force of the constraint,

Using the constraint equation 8 and the velocity of the knife contact point,

the set of equations above can be written more compactly as,

and

A more convenient set of variables is,

and

where

In terms of these variables, the set of equations above reads,

and

Besides these equations, we have the dynamical condition,

which comes from the expression for the kinetic energy. The relations (26), (27) and (29) suggest that the variables u₁ and u₂ can be written in sinusoidal forms:

where Ψ is an angle that can easily be related to the parameter λ . Putting the functions (30) and (31) in the equations (26) and (27), we obtain,

then,

In terms of the configuration coordinates the above equations read:

and

where,

This set of equations is usually obtained in the framework of the differential geometric formulation of nonholonomic mechanics [8] and u₁ = sin(Ψ) and u₂ = cos(Ψ) are called the controls of the system. Using a matrix notation and defining u = (u₁,u₂) ^Tthe set of equations (26), (27) and (32) can be integrated giving,

where J is the simpletic matrix,

3. THE AUTONOMOUS MOTION

Choosing χ = 0, the equations of motion (36) and (37) become,

These are the same equations obtained by Neimark and Fufaev [5] for the motion of the Chaplygin sleigh in the horizontal plane and free from external forces and torques.

4. THE CONTROLLED MOTION

The angle Ψ is related to the components of the center of mass velocity. Using the equations (34), (35) and the definitions of u₁ and u₂, we obtain,

Where is the component of the center of mass velocity in the direction of the longitudinal axis of the sleigh ( and of the knife ) and b is the transversal component. We introduce the variable,

where, |ρ| is the radius of curvature of the trajectory. Then the above equation reads,

The equation (45) is of fundamental importance in the process of controlling the system. It is this equation that determines the control parameter Ψ, for a prescribed path imposed to the system.

In order to clarify this detail of the controlling procedure we consider the problem of to compel the Chaplygin sleigh to follow a path described by a well behaved function y = y(x) in the plane (x,y) with finite derivatives y^'(x) = tanΦ and y^"(x). The radius of curvature of this path is given by,

Then, the angle of control Ψ is obtained from,

Under the above conditions we have tan(Ψ) ∈ (-∞,∞) and Ψ ∈

For a parametric curve x(s) , y(s) the equation (45) gives,

This kind of procedure by which the equations of motion of the system are determined such that the trajectory of the system follows on the prescribed path is the first stage of the control process sometimes called planning or tracking [9].

An immediate application of these results is the computation of the time of the motion along the given trajectory between two points s = 0 and s(t) .

The kinetic energy of the system is,

and can be rewritten as,

Then, the time of the motion is given by:

For a given input function x(s), y(s),

and the time expended along the motion is given by

5. THE CONTROL SYSTEM

In order to examine the physical aspects of the control process, we return to the constrained Lagrangian,

The angular momentum of the system

is not a conserved quantity because there is a torque:

or

This torque changes the angular momentum of the Chaplygin sleigh around the contact point of the knife which is shown by the equation of motion

This first term (- λ) is due to an external system which controls the motion of the Chaplygin sleigh. The second term is a torque due to the centrifugal force that appears in the accelerated frame fixed in the Chaplygin sleigh.

However, the formulation above requires that the kinetic energy

must be a constant along the controlled motion. The equations (26) and (27) give,

It is easy to see that if the system is under the action of a torque solely, the energy is not conserved. The kinetic energy is,

where,

then,

However, = and I = , which are a force applied on the center of mass and a torque, respectively.

Using these relations, we obtain:

If = 0 and ≠ 0 then ≠ 0.

In order to obtain a control system that does not change the kinetic energy, we must impose F_cs+( aF_cΦ+) = 0. Using = ρ , we obtain,

In the absence of a torque, = 0, the condition for energy conservation is

then, ⊥ and,

Introducing the following notation,

where c_c is the center of the curvature of the path, we obtain · = 0,then ||, and the force is applied in c in the direction of c_c.

In order to determine the force that must be applied on the CM for the system to follow a given path, we use the relations,

and

then

where

6. EXAMPLES OF TRACKING

The first example is the motion along a straigh line given by,

The angles of this trajectory are:

then,

and

which are all constants. The scalar velocity is,

and the equations of motion are,

The equations of the trajectory are,

A second example is the case of a circular trajectory with radius R,

Then

and the equation (45) gives,

which is a constant.

The period of circulation is

Besides the angle Ψ we have

then,

The angle χ which is the parameter that drives the system along the circular path is,

The time evolution is given by,

then,

The cartesian coordinates of the trajectory are given by,

Then,

and

is the angular velocity of the system along the circular trajectory. The time dependence of the driving angle is,

The third example consists of an input path given by the parametric equations of a catenary,

where s > 0 is the arc lengh of the path.

The radius of curvature is,

and the angle of control along this path is given by,

The parametric equation of the motion

reads,

and the time evolution of the system along the path is given by,

In order to obtain the equations of trajectory x = x(t) and y = y(t), we use the parametric equations of the input path x = x(s) and y = y(s), which give x = x(s(t)) and y = y(s(t)).

We integrate numerically the parametric equations of motion (102), with v_T = 1 and b = x_o = 1, obtaining s_j = s(t_j), x_j = x(s(t_j)) and y_j = y(s(t_j)) . The graphic of these results is shown in figure (2).

The force that drives the system along the catenary path can be easily obtained. The equations of the motion are,

and

From tan(Ψ) = ( x_o²+s²) / (bx_o) , we obtain

therefore, we are able to compute

As a fourth example, we consider a sinusoidal path y(x) = -Rsin(x/R) with R = 1. The equations of motion are,

The angles are given by,

then

which can be integrated to give x(t) and y(t) = -sin(x(t)).

The result of numerical integration of the above equation, which b = 1 and v_T = 1, is shown in figure (3).

Finally, we observe that, from the equation (21), we obtain,

where, at the right hand side, the first term is the constraint reaction and the second term is the centrifugal force acting on the system. In the straigh line and the circular trajectories we have = 0, the angular momentum, p_Φ = mb², is constant under the action of the control system and the constraint reaction and the centrifugal force are in equilibrium.

7. CONCLUSION

The equations of motion for nonholonomic nonautonomous controlled systems can be obtained by different methods. Differential geometry approaches to mechanics are usually employed to obtain the equation of motion for this kind of systems [8]. However, we used the vakonomic formulation [6], an extension of the lagrangian formulation in which the lagrangian function is added with a linear combination of the constraint conditions. The coefficients of this linear combination are the Lagrange multipliers which are the free parameters that permit to control the system. The next step is to solve the equations of motion using the free parameters to compel the system to follow a prescribed pathway. This procedure, usually called planning or tracking, requires a prescription that relates the free parameters, or control parameters, of the theory with the input function that describes the chosen trajectory. In this paper, we give a prescription to obtain the control angle Ψ of the Chaplygin sleigh. This control angle is given by tanΨ = where b is the radius of gyration of the system and ρ is the radius of curvature of the prescribed pathway. In the appendices we show some examples of Chaplygin systems that can be controlled with the same prescription. All these examples pertain to the class of the unicycles [9]. Some of these examples, the sleigh and the vertical disk, need to be controlled by external force and torque. However, the two wheeled carriage which has an internal degree of freedom can be controlled using internal torque and force. In a next paper, we intend to extend the present formulation to include the process of linear feedback or adaptative control [9]

(Received on 6 April, 2009)

APPENDIX A: A DISK ROLLING VERTICALLY ON A PLANE WITHOUT SLIPPING [8]

The parameters of this system are the mass m of the disc, the momentum of inertia I₁ relative to the axis and the momentum of inertia I₂ relative to a diameter.

The coordinates of this system are: the cartesian components (x,y) of the contact point with the plane, the angle of direction Φ that the plane of the disk forms with the axis x on the plane and the angle θ that denotes a rotation of the disk. In terms of these coordinates the kinetic energy of the disk reads,

Let 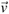= 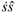be the velocity of the point of contact or the center of mass of the disk. Its cartesian components are:

Then the motion of the point of contact is constrained by the relation,

Besides this anti-transverse motion constraint, the motion of the disk is constrained by the nonslipping condition

This last relation can be used to rewrite the kinetic energy in the form

Defining the new variables,

The kinetic energy reads,

The vakonomic formulation can be used to obtain the equations of the motion from the extended lagrangian,

Similarly as was done for the Chaplygin sleigh, it can be shown that u₁ and u₂ are given by,

where Ψ is the angle of control given by,

with

APPENDIX B: A TWO-WHEELED CARRIAGE ROLLING ON A PLANE WITHOUT SLIPPING [8]

The parameters of this system are the radius R of the wheels, the lenght of the axis 2a, the mass m and the moments of inertia I₁ and I₂ of each wheel, the mass M, the principal moments of inertia I of the axis and platform relative to the vertical axis. In this car the center of mass coincides with the center of the axis between the wheels. Let 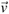= 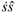be the velocity of the CM of the car. It cartesian components are,

which give the anti-transverse constraint

The rolling without slipping constraints on the wheels are,

Defining the new coordinates

The nonslipping constraints become,

The kinetic energy of the system is

Changing the variables

and using the nonslipping constraints we obtain

Defining the variables

The kinetics energy reads,

Using the vakonomic formulation with the extended lagrangian,

simmilarly as in the case of the Chaplygin sleigh, we can obtain the equations of the motion and show that u₁ and u₂ have the forms

The angle of the control Ψ is given by,

with

From the extended lagrangian we obtain the angular momentum of the system,

which is not conserved because there is a torque:

Using the constraint equation a = R we obtain,

This result shows that the two-wheeled car can be controlled by an internal torque that produces a difference in the acelerations of the wheels , and a force F_s.

APPENDIX C: COMPARING THE VAKONOMIC FORMULATION WITH HEURISTIC SOLUTION

In this appendix we show that, for the class of systems considered in this work, the results obtained using the vakonomic approach can also be obtained with an independent method. The prototype of these systems is the chaplygin sleigh moving on a horizontal plane. Using the same coordinates and the notations defined in the section II, the kinetic energy reads

The constraint condition is

and the scalar velocity of the point of contact of the knife is

Using these relations, the knife energy becomes

where b² = a²+I/m. The velocity of the center of gyration is

then v_T = We define

Then (π/2- Ψ) is the angle between the velocities

_T and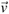 _A = 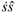. From the kinetic energy and the definition of Ψ we obtain,

The equations of motion of the system can be obtained using = cosΦ and = sinΦ, that give

These equations of motion depend on two parameters, v_T and Ψ which must be determined for a prescribed controlled motion of the system along a given path. Let the path be given by y = y(x). Its radius of curvature is

which is related to the scalar and angular velocities of the system by

The angle Ψ is then determined by

The second parameter of control v_T can be determined choosing a particular motion along this path. If the kinetic energy must be constant along the motion, then v_T = is constant. If the scalar velocity must be constant = v_s, v_T is given by

and the angular velocity is

The other equations of motion in this particular case are

APPENDIX D: COMPARING THE VAKONOMIC FORMULATION WITH THE LAGRANGE-D'ALEMBERT PRINCIPLE

The equations of motion for the chaplygin sleigh derived using the vakonomic formulation, equation (21-54), can be rewritten as

and

These are control equation that can be used to impose a prescribed path to the system.

For autonomous motion we must apply the Lagrange-D'Alembert (LD) principle. For the Chaplygin sleigh the lagrangian is

and the constraint condition reads

The equations of motion given by the LD principle are

with q = x,y,Φ, where µ is a Lagrange multiplier, and the constraint equation:

After some algebra, we obtain the equations of motion:

and the force of constraint:

It is well known that the set of vakonomic equations (D2-D6) and the set of LD equations (D12-D14) are not, in general, dynamically equivalents, in the sense that there are not any initial condition λ(t = 0) such that the solutions of both sets give the same trajectory in the configuration space [16]. The vakonomic formalism does not describe the autonomous motion of the system. It is a kind of prescritive mechanics which can be used to describe the motion of a nonholonomic system along a prescribed path in the configuration space.

• [1] H. Hertz, Die Prinzipien der Mechanik Gesammelte Werke, vol. 3, Barth, Leipzig, 1894.
• [2] H. Goldstein, Classical Mechanics Addison Wesley Publishing Company University Moscow, 1970.
• [3] F. Gantmacher, Lectures in Analytical Mechanics Mir Publisher University Moscow, 1970.
• [4] C. Lanczos, The Variational Principles of Mechanics London: University of Toronto press, 1974.
• [5] J. I. Neimark and N. A. Fufaev, Dynamics of Nonholonomic Systems (Translations of Mathematical Monographs, vol. 33), American Mathematical Society, Providence, RI, 1972.
• [6] V. I. Arnold, V. V. Kozlov and A. I. Neishtadt, Dynamical Systems Vol. III, Springer-Verlag, New York-Heidelberg-Berlin, 1988.
• [7] S. A. Chaplygin, "On theory of motion of nonholonomic systems, The reducing multiplier theorem". Math. Collection. vol. 28, no. 2, pp. 303-314, 1911.
• [8] A. M. Vershik and V. Y. Gershkovich,"Nonholonomic problems and the theory of distributions," Acta Applic. Math., vol. 12, pp. 181-209, 1988.
• [9] C. C. de Wit, B. Siciliano and G. Bastin (The Zodiac), Theory of Robot Control, London: Springer-Verlag, 1997.
• [10] P. Pitanga, Quantization of a nonholonomic system with symmetry N. Cimento, vol. 109B, pp. 583-594, 1994.
• [11] P. Pitanga and P. R. Rodrigues, Projection methods for some constrained systems Rendiconti di Matematica, vol. 23, pp. 303-328, 2003.
• [12] A. S. Sumbatov, Nonholonomic systems Regular and chaotic dynamics, vol. 7, no. 2, pp. 221-238, 2002.
• [13] N. H. Getz and J. E. Marsden, Control for an autonomous bicycle in Proc. IEEE Int. Conf. Robotics and Automation, (Nagoya, Japan), 1397-1402.
• [14] S. Martínez, J. Cortés and M. de León, The geometric theory of constraints applied to the dynamics of vakonomic mechanical systems. The vakonomic bracket J. Math. Phys., vol. 41, pp. 2090-2120, 2000.
• [15] J. C. Monforte, Geometric, control and numerical aspects of nonholonomic systems, Springer-Verlag, 2002.
• [16] O. E. Fernandez and A. M. Bloch, Equivalence of the dynamics of nonholonomic and variational nonholonomic systems for certain initial data, J. Phys. Math. Theor., vol. 41, pp. 344005, 2008.

Publication Dates

• Publication in this collection
  23 June 2010
• Date of issue
  June 2010

History

• Received
  06 Apr 2009