Abstract
Conservation of the bubble size distribution function was applied to the reactive absorption of carbon dioxide in a bubble column reactor. The model developed was solved by the method of characteristics and by a Monte Carlo method. Simulations were carried out using simplified models for the liquid phase and for the gas-liquid mass transfer. Predictions of gas holdup and outlet gas composition showed that the concept of a mean bubble diameter is not applicable when the bubble size distribution is reasonably polydispersed. In these cases, the mass mean velocity and the numerical mean velocity of the bubbles are very different. Therefore, quantification of the polydispersion of bubbles was shown to be essential to gas-phase hydrodynamics modeling.
bubble column; size distribution; absorption; polydispersion; bubble; Monte Carlo
Conservation of bubble size distribution during gas reactive absorption in bubble column reactors
P. L.C. LAGE
Programa de Engenharia Química, COPPE/UFRJ, C. P. 68502, 21945-970, Rio de Janeiro - RJ,
Phone (021) 590-2241, Fax (021) 290-6626
E-mail: paulo@peq.coppe.ufrj.br
(Received: July 22, 1999; Accepted : August 26, 1999)
Abstract - Conservation of the bubble size distribution function was applied to the reactive absorption of carbon dioxide in a bubble column reactor. The model developed was solved by the method of characteristics and by a Monte Carlo method. Simulations were carried out using simplified models for the liquid phase and for the gas-liquid mass transfer. Predictions of gas holdup and outlet gas composition showed that the concept of a mean bubble diameter is not applicable when the bubble size distribution is reasonably polydispersed. In these cases, the mass mean velocity and the numerical mean velocity of the bubbles are very different. Therefore, quantification of the polydispersion of bubbles was shown to be essential to gas-phase hydrodynamics modeling.
Keywords: bubble column, size distribution, absorption, polydispersion, bubble, Monte Carlo.
INTRODUCTION
Bubble column reactors have a very complex hydrodynamic behavior. They are usually modeled by the idealization of a plug-flow reactor with axial dispersion (axial dispersion models). However, this modeling produces results for the effective gas-phase dispersion that are in disagreement with experimental values (Deckwer and Schumpe, 1993). This occurs due to the inadequacy of the axial dispersion model for the gas phase.
Recently Hyndman and Guy (1995a, 1995b) and Hyndman et al. (1997) have experimentally shown that the gas phase in a bubble column has to be modeled by the movement of its bubbles, i.e., a convective model is necessary. Experimentally determined bubble dispersion has been explained by the existence of a distribution for the ascension velocities of bubbles. However, the use of the absolute bubble ascension velocity as independent variable in the distribution function does not allow an evaluation of the separate effects of bubble size distribution and liquid-phase velocity field. Besides, correlations are required to determine the parameters present in these distribution functions.
On the other hand, Fleischer et al. (1996) developed a model for the reactive absorption of carbon dioxide in sodium hydroxide solutions that uses an axial dispersion model for the liquid phase and a gas-phase model based on the conservation of the bubble size distribution function. The formulation of their model restricts its applicability to the absorption of a pure gas when changes in the gas density can be neglected. The chemical enhancement factor for the gas absorption reaction had been determined a priori by a double film model. Fleischer et al. (1996) included the terms for bubble breakup and coalescence in their model. However, their experimental data for large bubbles (4 mm in diameter) indicate that breakup and coalescence had a negligible effect in that case. These data also show that it could be assumed that the liquid phase was well mixed. Results were presented only for monodispersed initial bubble distributions, with little attention given to the evolution of the bubble size distribution along the bubble column height.
In this work, a gas-phase model was developed for reactive absorption in a bubble column reactor based on the conservation of the bubble size distribution function (population balance), which was applied to carbon dioxide absorption in aqueous solutions of sodium hydroxide. For sodium hydroxide concentrations above 0.1 molar, bubble coalescence is practically suppressed (Zahradník et al., 1995), which allows the effects of bubble coalescence and breakup in the gas-phase model to be neglected for the time being. This agrees with some of the experimental data of Fleischer et al. (1996). In addition, homogeneous bubbling regime with a well-mixed liquid phase and a constant sodium hydroxide concentration is assumed. This allows the implementation of the gas-phase model, but restricts its applicability to the initial stages of a semi-batch absorption process or to a continuous absorption process.
The present aim is the analysis of the effect the polydispersion of bubbles on mass transfer and gas holdup in bubble columns. The use of a mean bubble size in this bubbling process was also studied.
CONSERVATION OF THE BUBBLE SIZE DISTRIBUTION FUNCTION
Particle, drop or bubble polydispersion in a given process is characterized by a distribution function which is a function of the size (mass, volume or equivalent diameter), composition and any other relevant bubble variable. For a bubbling process with mass transfer and variable gas density, it is convenient to define this size distribution function using the mass of each chemical species that may be present in the gas phase (mi, i = 1, n).
Let f(t,x,mi) be the normalized distribution function and N(t,x) be the number of bubbles per unit volume (number density). Then, the conservation equation for the bubble distribution function can be written as
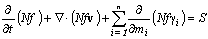
(1)
where S stands for the terms that model the breakup and coalescence phenomena.
Since f is normalized, it is possible to integrate Equation (1) over mi, "i, which gives the conservation equation for the bubble number density
 (2)
(2)
where
 (3)
(3)
The mass balance for the gas phase is obtained with the first moment of Equation (1) in relation to  , which, after some algebraic manipulation, gives
, which, after some algebraic manipulation, gives
 (4)
(4)
where
 (5)
(5)
 (6)
(6)
Using the definitions of gas holdup,  , and of gas mean density,
, and of gas mean density,  , the mass balance is written by the well-known formulae
, the mass balance is written by the well-known formulae
 (7)
(7)
BUBBLE COLUMNS IN THE HOMOGENEOUS REGIME
The present analysis assumes the following hypotheses: pseudo steady-state, homogeneous bubbling regime, binary gas mixture, only one gas component soluble in the liquid phase, one-dimensional problem and no effect of bubble breakup or coalescence (S = 0). Using these assumptions, we have N = N(z) and f = f(z,m1,m2), where the subscript 1 indicates the component that can be absorbed. Thus, Equations (1) and (2) can be simplified to
 (8)
(8)
 (9)
(9)
because g2 = 0. In these equations, v(z,m1,m2) is the bubble velocity and  is the corresponding numeric mean velocity.
is the corresponding numeric mean velocity.
Equation (9) can be integrated from a given inlet condition to give
 (10)
(10)
Using Equation (10), we can rewrite Equation (8) as
 (11)
(11)
which must be integrated from the inlet condition z = 0, f(m1,m2,z) = fe(m1,m2,0). It should be noted that the m2 variable in Equation (11) appears as a parameter in the functional dependence of f, v and g1.
Equation (11) gives a hyperbolic initial value problem which can be solved by the method of characteristics. After some algebraic manipulation, the equations that determine the characteristic curves in the (z,m1,m2,f) space are given by
 (12)
(12)
 (13)
(13)
 (14)
(14)
 (15)
(15)
which should be integrated from the initial conditions t = 0, z = 0, m1 = m1e, m2 = m2e and f = fe.
The mapping from (z,m1,m2) to (t ,m1e,m2e) is proper at t = 0 if ve ¹ 0, i.e., if the bubble really enters the column. Thus, the solution for Equations (12) to (15) gives the solution for the initial value problem given by Equation (11) in a neighborhood of t = 0 (Courant and Hilbert, 1989). Since Equation (11) is semi-linear, there is no shock development in the solution, thus allowing use of the method of characteristics to solve for all t > 0 (Whitham, 1974). In addition and for the same reason, Equations (12), (13) and (14) can be solved independently from Equation (15), which allows the calculation of the characteristic base curves once and for all (Aris and Amundson, 1973). This requires little computational effort in the solution of this population balance problem.
Finally, it is clear from Equations (12), (13) and (14) that the variable along each characteristic curve, t , corresponds to the ascension time for each bubble. Thus, each characteristic base curve can be individually drawn from the solution of the problem of mass transfer during the ascension of a characteristic bubble, which has the properties determined by one of the characteristic curves.
MODEL FOR MASS TRANSFER FROM A BUBBLE
Siciliano et al. (1997) developed a simplified model to calculate the mass transfer from a bubble during the reactive absorption of a mixture of carbon dioxide (component 1) and air (component 2) in alkali solutions. This model was used to draw the characteristic base curves, assuming that the bubbles were injected at the terminal ascension velocity for its initial conditions. Then the one-dimensional trajectory, velocity, composition and density of each bubble were calculated during its ascension. Penetration theory was used to determine the mass transfer coefficient, assuming a spherical bubble with a free-moving interface and a pseudo first-order absorption reaction. Gas-phase mass transfer resistance was neglected, although there is some evidence that it may be important (Souza, 1997). More details are given in the original reference (Siciliano et al., 1997).
GAS HOLDUP
Gas holdup can be determined from bubble number density and mean bubble volume by
 (16)
(16)
Using Equation (10) with
 (17)
(17)
we have
 (18)
(18)
which is a well-known formulae, showing that  corresponds to the interstitial gas-phase velocity. It should be noted that
corresponds to the interstitial gas-phase velocity. It should be noted that  , even though several analyses of particulate systems (bubble columns, pneumatic transport, etc.) assume that
, even though several analyses of particulate systems (bubble columns, pneumatic transport, etc.) assume that  is equal to uG, which is valid only when the particles are monodispersed (see Equations (3), (5) and (6)).
is equal to uG, which is valid only when the particles are monodispersed (see Equations (3), (5) and (6)).
The overall gas holdup is calculated by
 (19)
(19)
MONTE CARLO METHOD
The Monte Carlo method was applied to the problem described above, in order to compare its results to those obtained by the method of characteristics. The Monte Carlo method basically consists of choosing a relatively large number of bubbles, with initial conditions randomly chosen according to a given initial distribution, and simulating the mass transfer process for each one of these bubbles. Then the mean values for extensive variables are obtained using
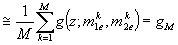 (20)
(20)
An estimate of the error can be obtained by the application of the central limit theorem, using some subgroups of the sampling space. Thus, if there are J subgroups with j = M/J bubbles, the variance in a property estimate is calculated by
 (21)
(21)
where gj are the estimates of  using the j elements of each one of the J subgroups. Considering a confidence level of 99%, we have
using the j elements of each one of the J subgroups. Considering a confidence level of 99%, we have  Î [gM- 2,58 dJ, gM+ 2,58 dJ].
Î [gM- 2,58 dJ, gM+ 2,58 dJ].
NUMERICAL PROCEDURE
Equations (12) and (14) were solved using the Siciliano et al. model (1997), slightly modified in order to perform the integration along the z instead of the t variable. The integration was implemented using the DASSL routine (Petzold, 1989).
The operational conditions and an overall gas holdup estimate were used to simulate the behavior of a given number of characteristic bubbles, C, with a constant initial concentration and sizes distributed within a selected range for the analysis. The values for the nonhomogeneous term of Equation (15), G, were stored in a z grid and, therefore, known at several t values, for each of the characteristic bubbles. The partial derivatives that appear in the definition of G, as given by Equation (15), were determined at each z grid point by numerical perturbation. Equation (15) can be integrated between consecutive z grid points, giving
 (22)
(22)
which was used to simultaneously integrate for all characteristic bubbles between consecutive points in the z grid, using an initial condition for f determined from a given initial bubble distribution. The value of  at zn+1 in Equation (22) depends on distribution f at the same point and it was obtained by iteration, using the value of
at zn+1 in Equation (22) depends on distribution f at the same point and it was obtained by iteration, using the value of  at zn as the initial guess. The G integral in Equation (22) was obtained by the trapezoidal quadrature.
at zn as the initial guess. The G integral in Equation (22) was obtained by the trapezoidal quadrature.
For the results of this work, which are described in the next section, Equations (12) to (14) were integrated using an absolute tolerance of 10-10 and a relative tolerance of 10-6. The exponential factor in Equation (22) was shown to be close to one for the present conditions, introducing a very small correction to the distribution function calculated with G = 0. As expected, the ¶g1/¶z term present in the definition of G was shown to be extremely small because it originated only by the change in bubble size caused by a variation in gas density as a function of z. For the integration tolerances employed, the values obtained for this term were affected by the numerical truncation error, oscillating in sign as m1 changes. In order to avoid the presence of these small oscillations in the solution of the distribution function, the term (v/g1¶g1/¶z) was been neglected in the calculation of the G values used in Equation (22). The results presented in the next section correspond to the distribution functions obtained with this approximation, which are virtually identical to those obtained with G = 0. In any case, the approximation given by G = 0, i.e.,
 , (23)
, (23)
is very good. In this work, it has been assumed that the initial bubble size distribution function is given by a log-normal distribution based on bubble diameters, written as
 (24)
(24)
When g1 became smaller than the precision used in the calculations, Equation (22) was substituted by  , which is valid for no mass transfer. Following the procedure described above, where the base characteristic curves are calculated first, the problem is solved by integrating C times a system of four ordinary differential equations (Siciliano et al. model, 1997) instead of integrating a system of 4C ordinary differential equations.
, which is valid for no mass transfer. Following the procedure described above, where the base characteristic curves are calculated first, the problem is solved by integrating C times a system of four ordinary differential equations (Siciliano et al. model, 1997) instead of integrating a system of 4C ordinary differential equations.
Then, knowing the bubble distribution function,  ,
,  , N and e were calculated with Equations (3), (6), (10) and (18), respectively, by using the Simpson quadrature for non-equal intervals (Minkowycz et al., 1988). The values of
, N and e were calculated with Equations (3), (6), (10) and (18), respectively, by using the Simpson quadrature for non-equal intervals (Minkowycz et al., 1988). The values of  in Equation (5) and
in Equation (5) and  from a similar definition were determined and used to calculate the mean mass fraction of carbon dioxide in the gas phase,
from a similar definition were determined and used to calculate the mean mass fraction of carbon dioxide in the gas phase,  .
.
In these equations, the double integration in relation to m1 and m2 was reduced to a single integration in m, by the assumption of a constant initial composition for all bubbles that are injected into the column (Y1e = constant = Y10). This can be deducted from f(z,m1,m2) dm1 dm2 = f1(z,me,Y1e) dme dY1e because m1 = m1(z,me,Y1e) and m2 = (1-Y1e) me. In addition, since f1(z,me,Y1e) = f2(z,me) d (Y1e - Y10) and m = m(z,me,Y10), for any variable, g, we can write that
 (25)
(25)
The Simpson quadrature was also used to calculate an updated value for the overall gas holdup, eT, from Equation (19). This value was compared to the initial estimate and the whole procedure was repeated until convergence was reached. Two iterations sufficed for all the cases analyzed.
The calculations expressed by Equations (20) and (21) were used to determine  , e ,
, e ,  and
and  along the z variable, allowing
along the z variable, allowing  determination. The bubble number density, N, was obtained from Equations (10) and (17), and the standard deviation of
determination. The bubble number density, N, was obtained from Equations (10) and (17), and the standard deviation of  was estimated from those for
was estimated from those for  and
and  .
.
RESULTS AND DISCUSSION
The results that are presented here were obtained for the simulation of the reactive absorption of a mixture of carbon dioxide and air with  and a superficial gas velocity of 3.61 cm/s in a 0.2 molar solution of sodium hydroxide. The column was assumed to have a diameter of 7 cm and a height of 1 meter and was operated at 298 K. In order to simplify the calculations, physical properties of pure water were used for the liquid phase. Moreover, a log-normal distribution with d50 = 0.01 m and several values for s was assumed for the injected bubbles, which is in accordance with some experimental data (Lage and Espósito, 1999). For these cases, it was found that C = 80 and a uniform z grid with 21 points were enough to obtain converged results.
and a superficial gas velocity of 3.61 cm/s in a 0.2 molar solution of sodium hydroxide. The column was assumed to have a diameter of 7 cm and a height of 1 meter and was operated at 298 K. In order to simplify the calculations, physical properties of pure water were used for the liquid phase. Moreover, a log-normal distribution with d50 = 0.01 m and several values for s was assumed for the injected bubbles, which is in accordance with some experimental data (Lage and Espósito, 1999). For these cases, it was found that C = 80 and a uniform z grid with 21 points were enough to obtain converged results.
The results for the evolution of the bubble distribution function F(z,de) for s = 1.1 and 1.5 are shown in Figure 1, which also shows the converged values for eT. Comparing the distributions shown in these figures, it is easy to note the effect of bubble size polydispersion. For s = 1.1, the size distribution function changes very little along z. On the other hand, for s = 1.5, the larger bubbles pass through the column very quickly, undergoing little absorption, while the smaller bubbles are highly absorbed, becoming even smaller, which leads to a reduction in ascension velocity, increasing their number densities. From a given height on (between 0.25 and 0.50 m), the smaller bubbles consist of pure air and, consequently, they expand as the hydrostatic pressure drops. This can be seen in Figure 1b, noting the movement of the maximum value of F(z,de) to larger diameters.
Table 1 lists the converged results obtained for NT, eT, q and  for several s values. Monte Carlo results for s = 1.1 (M = 400, J = 20) and the results obtained by using the Sauter mean diameter are also shown. The gas holdup value obtained by the Akita and Yoshida (1974) correlation is also given in Table 1. As s increases, q and NT drop due to the formation of large bubbles, which ascend quickly in the column, resulting in a decrease in eT. In addition, as the larger bubbles have smaller specific areas and residence times,
for several s values. Monte Carlo results for s = 1.1 (M = 400, J = 20) and the results obtained by using the Sauter mean diameter are also shown. The gas holdup value obtained by the Akita and Yoshida (1974) correlation is also given in Table 1. As s increases, q and NT drop due to the formation of large bubbles, which ascend quickly in the column, resulting in a decrease in eT. In addition, as the larger bubbles have smaller specific areas and residence times,  increases as s increases.
increases as s increases.
The Monte Carlo results are in agreement with those obtained from the conservation equation for the distribution function, even for the small M value used. The error represented for  corresponds to a 99% confidence level. It should be noted that the Akita and Yoshida (1974) correlation predicts an overall gas holdup value comparable to that obtained for the smaller s value. As s increases, differences of almost 100% are observed between the present results and the correlation predictions.
corresponds to a 99% confidence level. It should be noted that the Akita and Yoshida (1974) correlation predicts an overall gas holdup value comparable to that obtained for the smaller s value. As s increases, differences of almost 100% are observed between the present results and the correlation predictions.
The Sauter mean diameters for the log-normal distribution with d50 = 0.01 m and s = 1.1, 1.3 and 1.5 are given by d32 = 0.0102, 0.0119 and 0.0151 m, respectively. These values were used to calculate the NT, T, q, and  values shown in Table 1. The use of the Sauter mean diameter leads to errors of 72% in
values shown in Table 1. The use of the Sauter mean diameter leads to errors of 72% in  and 81% in eT for s = 1.5, which shows that this procedure is not adequate when the polydispersion of bubble properties (size, composition, etc.) is appreciable.
and 81% in eT for s = 1.5, which shows that this procedure is not adequate when the polydispersion of bubble properties (size, composition, etc.) is appreciable.
Figures 2, 3, 4 and 5 show the behavior along the z variable for the number density, mean velocities, gas holdup and mean mass fraction of carbon dioxide in the gas phase, respectively, for s = 1.1, 1.3 and 1.5. Monte Carlo results for s = 1.1 are also depicted in these figures, showing good agreement with the results obtained by the conservation of the distribution function. Figures 2 and 4 show the polydispersion effect on NT and e, which is caused by the increasing fraction of the gas phase that is carried as large bubbles as the s value increases. Figure 3 shows clearly the difference between  and
and  , which increases as the s value increases. Thus, the use of
, which increases as the s value increases. Thus, the use of  in Equation (7) is incorrect for systems with a large degree of polydispersion of bubble size.
in Equation (7) is incorrect for systems with a large degree of polydispersion of bubble size.
The carbon dioxide mass fraction profiles along the column height are shown in Figure 5. They also indicate the effect of the increasing presence of larger bubbles as the s value increases. Large bubbles have smaller specific areas and residence times, losing less mass than the smaller bubbles. Outlet values for  , which are listed in Table 1, show large differences between the values obtained for different s values.
, which are listed in Table 1, show large differences between the values obtained for different s values.
CONCLUSIONS
A theoretical and numerical analysis of the conservation of the bubble distribution function in bubble columns was used to simulate the reactive absorption of carbon dioxide in homogeneous bubbling processes. A Monte Carlo method was also utilized to solve the same problem. Comparison of the results obtained with both methodologies showed good agreement.
Predictions of gas holdup and outlet gas composition have been used to show the inadequacy of use of the Sauter mean bubble diameter when the polydispersion of bubble size is appreciable. In these cases, it was also shown that there is a large difference in the values for mass and numeric mean bubble velocities, which are usually considered equal in the models that ignore polydispersion of bubble size. It could be concluded that the quantification of size polydispersion is essential to the modeling of gas-phase hydrodynamics in bubble columns.
ACKNOWLEDGEMENTS
The author would like to acknowledge the financial support received from CNPq, grant number 520660/98-6.
NOMENCLATURE
< > mass mean
C number of characteristic bubbles
d diameter (m)
de equivalent diameter (m)
d50 parameter in log-normal distribution (m)
d32 Sauter mean diameter (m)
f size distribution function (kg-n)
F size distribution function in terms of the equivalent diameter (m-1)
G nonhomogeneous term of Equation (15)
g generic extensive variable
j bubble flux (m-2 s-1)
m bubble mass (kg)
vn number of gas-phase components
N bubble number density (m-3)
NTnumber of bubbles in column
M number of events in Monte Carlo method
q bubble formation frequency (s-1)
u superficial velocity (m/s)
v velocity vector of bubble (m/s)
v vertical velocity of bubble (m/s)
V bubble volume (m3)
S rate of bubble breakup and coalescence (s-1m-3kg-n)
t time (s)
Y mass fraction
z vertical coordinate (m)
Z column height (m)
Greek letters
d standard deviation
e gas holdup
g rate of increase of bubble mass (kg/s)
G rate of increase of gas-phase mass (kg m-3s-1)
r density (kg/m3)
s parameter in log-normal distribution
t ascension time coordinate (s)
Subscripts
e column inlet
i chemical species (1 for carbon dioxide)
G gas phase
m mass basis
T whole column
Superscripts
numeric mean
- Akita, K. and Yoshida, F., Bubble Interfacial Area and Liquid Phase Mass Transfer Coefficient in Bubble Columns, Ind. Eng. Chem. Proc. Des. Dev., Vol. 13, 84 (1974).
- Aris, R. and Amundson, N. R., Mathematical Methods in Chemical Engineering First
- Order Partial Differential Equations with Applications. Vol. 2, Prentice-Hall, Englewood Cliffs (1973).
- Courant, R. and Hilbert, D., Methods of Mathematical Physics. Vol. 2, Wiley-Interscience, New York (1989).
- Deckwer,W.-D. and Schumpe, A., Improved tools for bubble column reactor design and scale-up, Chem. Engng. Sci., Vol. 48, 889-911 (1993).
- Fleischer, C., Becker, S. and Eigenberger, G., Detailed Modelling of the Chemisorption of CO2 into NaOH in a Bubble Column, Chem. Engng. Sci., Vol. 51, 1715-1724 (1996).
- Hyndman, C. L. and Guy, C., Gas Phase Flow in Bubble Columns: A Convective Phenomenon, Can. J. Chem. Engng., Vol. 73, 426-434 (1995a).
- Hyndman, C. L. and Guy, C., Gas-Phase Hydrodynamics in Bubble Columns, Trans. IChemE: Part A, Vol. 73, 302-307 (1995b).
- Hyndman, C. L., Larachi, F. and Guy, C., Understanding Gas-Phase Hydrodynamics in Bubble Columns: A Convective Model Based on Kinetic Theory, Chem. Engng. Sci., Vol. 52, 63-77 (1997).
- Lage, P. L. C. and Espósito, R. O., Experimental Determination of Bubble Size Distributions in Bubble Columns: Prediction of Mean Bubble Diameter and Gas Holdup, Powder Technology, Vol. 101, No. 2, 142-150 (1999).
- Minkowycz, W. J., Sparrow, W. M., Schneider, G. E. and Pletcher, R. H., Handbook of Numerical Heat Transfer. Wiley-Interscience, New York (1988).
- Petzold, L. R., DASSL code, version 1989, Computing and Mathematics Research Division, Lawrence Livermore National Laboratory, L316, Livermore, CA (1989).
- Siciliano, A. M., Marinho, M. R. and Lage, P. L. C., Um Modelo Simplificado para a Absorçăo Reativa de Bolhas Ascendentes em Colunas de Borbulhamento, Proceedings of XXV ENEMP, Vol. 1, 219-226 (1997).
- Souza, A. L., Transferęncia de Massa com Reaçăo Química em Processos de Borbulhamento. M. Sc. thesis, FEQ, UNICAMP, Campinas (1997).
- Whitham, G. B., Liner and Nonlinear Waves. John Wiley & Sons, New York (1974).
- Zahardník, J., Fialova, M., Kastánek, F., Green, K. D. and Thomas, N. H., The Effect of Electrolytes on Bubble Coalescence and Gas Holdup in Bubble Column Reactors. Trans. IChemE: Part A, Vol. 73, 341-346 (1995).
Publication Dates
-
Publication in this collection
01 Mar 2000 -
Date of issue
Dec 1999
History
-
Accepted
26 Aug 1999 -
Received
22 July 1999










