Marcinkiewicz strong laws for linear statistics of rho*-mixing sequences of random variables

Abstracts

Strong laws are established for linear statistics that are weighted sums of a random sample. We show extensions of the Marcinkiewicz-Zygmund strong laws under certain moment conditions on both the weights and the distribution. These not only generalize the result of Bai and Cheng (2000, Statist Probab Lett 46: 105-112) to rho*-mixing sequences of random variables, but also improve them.

rho*-mixing; Marcinkiewicz-Zygmund strong laws; weighted sums

Leis fortes são estabelecidas para estatísticas lineares que são somas ponderadas de uma amostra aleatória. Mostramos extensões das leis fortes de Marcinkiewicz-Zygmund sob certas condições tanto nos pesos quanto na distribuição. Estas últimas não só generalizam o resultado de Bai e Cheng (2000, Statist Probab Lett 46: 105-112) para sequências aleatórias "ro*-mixing" como também o melhoram.

"ro*-mixing"; Marcinkiewicz-Zygmund leis fortes; somas ponderadas

MATHEMATICAL SCIENCES

Marcinkiewicz strong laws for linear statistics of r^*-mixing sequences of random variables

Guang-Hui Cai

Department of Mathematics and Statistics, Zhejiang Gongshang University, Hangzhou 310035 P. R. China

ABSTRACT

Strong laws are established for linear statistics that are weighted sums of a random sample. We show extensions of the Marcinkiewicz-Zygmund strong laws under certain moment conditions on both the weights and the distribution. These not only generalize the result of Bai and Cheng (2000, Statist Probab Lett 46: 105–112) to r*-mixing sequences of random variables, but also improve them.

Key words: r*-mixing, Marcinkiewicz-Zygmund strong laws, weighted sums.

RESUMO

Leis fortes são estabelecidas para estatísticas lineares que são somas ponderadas de uma amostra aleatória. Mostramos extensões das leis fortes de Marcinkiewicz-Zygmund sob certas condições tanto nos pesos quanto na distribuição. Estas últimas não só generalizam o resultado de Bai e Cheng (2000, Statist Probab Lett 46: 105-112) para sequências aleatórias "r*-mixing" como também o melhoram.

Palavras-chave: "r*-mixing", Marcinkiewicz-Zygmund leis fortes, somas ponderadas.

1 INTRODUCTION

As Bai and Cheng (2000) remarked, many useful linear statistics based on a random sample are weighted sums of i.i.d. random variables. Examples include least-squares estimators, nonparametric regression function estimators and jackknife estimates, among others. In this respect, studies of strong laws for these weighted sums have demonstrated significant progress in probability theory with applications in mathematical statistics. But a random sample is often dependent. So we want to know if the results obtained for i.i.d. random variables are still true for r*-mixing sequences of random variables.

Let S,T Ì be nonempty and define _S = s(X_k, k Î S), and the maximal correlation coefficient = sup corr(f, g) where the supremum is taken over all (S, T) with dist(S, T) > n and all f Î L₂(_S), g Î L₂(_T) and where dist(S, T) = inf_{x Î S, y Î T}|x - y|.

A sequence of random variables {X_n, n > 1} on a probability space {W, , P} is called r*-mixing if

As for r*-mixing sequences of random variables, one can refer to Bryc and Smolenski (1993), who found bounds for the moments of partial sums for a sequence of random variables satisfying (1.1), and to Peligrad (1996) for CLT, Peligrad (1998) for invariance principles, Peligrad and Gut (1999) for the Rosenthal type maximal inequality, Utev and Peligrad (2003) for invariance principles of nonstationary sequences. The main purpose of this paper is to establish the Marcinkiewicz-Zygmund strong laws for linear statistics of r*-mixing sequences of random variables. The results obtained (see Theorem 2.1 and Corollary 2.1) not only generalize the result of Bai and Cheng (2000) to r*-mixing sequences of random variables, but also improve them. In Theorem 2.2 of Bai and Cheng (2000), they believe the choice of b_n can hardly be improved in view of Cuzick (1995, Lemma 2.1), but now we improve the choice of b_n using a new method.

2 THE MARCINKIEWICZ-ZYGMUND STRONG LAWS

Throughout this paper, C will represent a positive constant though its value may change from one appearance to the next, and a_n = O(b_n) will mean a_n < Cb_n.

In order to prove our results, we need the following lemma.

LEMMA 2.1. (Utev and Peligrad, 2003). Let {X_i, i > 1} be a r*-mixing sequence of random variables, EX_i= 0, E|X_i|^p< ¥ for some p > 2 and for every i > 1. Then there exists C = C(p), such that

THEOREM 2.1. Let {X, X_i, i > 1} be a r*-mixing sequence of identically distributed random variables, T_n= a_niX_i, n > 1, where the weights {a_ni, 1 < i < n, n > 1} are random variables which are independent of {X_i, i > 1} (the case of deterministic weights is included). Suppose that for some a with 0 < a < 2 we have that

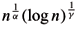|a_ni|^a = O(n) almost surely. If 1 < a < 2, we assume additionally that EX = 0. Set b_n= . We assume that for some h, g > 0, we have

Then

PROOF. "i > 1, define = X_iI(|X_i| < b_n), , then "e > 0,we have

First we show that

By |a_ni|ª = O(n) and Hölder inequality "1 < k < a, then

When 1 < a < 2, using EX = 0, (2.4), Markov inequality and (2.0), when n ® ¥, then

|a_ni|^a = O(n) implies that max_1<i<n |a_ni| = O(). By this and Hölder inequality, "k >a, then

When 0 < a < 1, using (2.6), Markov inequality and (2.0), when n ® ¥, then

From (2.5) and (2.7), Hence (2.3) is true.

From (2.2) and (2.3), it follows that for n large enough

Hence we need only to prove that

From the fact that E exp(h|X|^g) < ¥, it follows easily that

By Lemma 2.1, it follows that for q > 2

Let max(2, a, g + 1) < q, using (2.6), we have

By 0 < a < 2, (2.6) and q > (g + 1), we have

Putting (2.11) and (2.12) into (2.10) yields II < ¥. Now we complete the prove of Theorem 2.1.

COROLLARY 2.1. Under the conditions of Theorem 2.1, then = 0 a.s.

PROOF. By (2.1), we have

By Borel-Cantelli Lemma, we have

Hence

and using

We have

REMARK 2.1. Corollary 2.1 generalizes the Theorem 2.2 of Bai and Cheng (2000) to r*-mixing sequences of random variables and the restricton of b_n in Corollary 2.1 is weaker than the restricton of b_n in Theorem 2.2 of Bai and Cheng (2000).

ACKNOWLEDGMENTS

The author would like to thank an anonymous referee for his/her valuable comments. Research supported by National Natural Science Foundation of China.

Manuscript received on April 4, 2006; accepted for publication on August 1st, 2006; presented by MANFREDO DO CARMO

E-mail: [e-mail]

AMS Classification: 60F15; 62G05

• BAI ZD AND CHENG PE. 2000. Marcinkiewicz strong laws for linear statistics. Statist Probab Lett 46: 105-112.
• BRYC W AND SMOLENSKI W. 1993. Moment conditions for almost sure convergence of weakly correlated random variables. Proc Amer Math Soc 2: 629-635.
• CUZICK J. 1995. A strong law for weighted sums of i.i.d. random variables. J Theoret Probab 8: 625-641.
• PELIGRAD M. 1996. On the asymptotic normality of sequences of weak dependent random variables. J Theoret Probab 9: 703-715.
• PELIGRAD M. 1998. Maximum of partial sums and an invariance principle for a class weak dependent random variables. Proc Amer Math Soc 126: 1181-1189.
• PELIGRAD M AND GUT A. 1999. Almost sure results for a class of dependent random variables. J Theoret Probab 12: 87-104.
• UTEV S AND PELIGRAD M. 2003. Maximal inequalities and an invariance principle for a class of weakly dependent random variables. J Theoret Probab 16: 101-115.

Publication Dates

• Publication in this collection
  28 Nov 2006
• Date of issue
  Dec 2006

History

• Received
  04 Apr 2006
• Accepted
  01 Aug 2006