Spectral properties of the preconditioned AHSS iteration method for generalized saddle point problems

Spectral properties of the preconditioned AHSS iteration method for generalized saddle point problems

Zhuo-Hong Huang; Ting-Zhu Huang

School of Applied Mathematics, University of Electronic Science and Technology of China Chengdu, Sichuan, 610054, P.R. China

E-mails: [e-mail] / [e-mail] / [e-mail]

ABSTRACT

In this paper, we study the distribution on the eigenvalues of the preconditioned matrices that arise in solving two-by-two block non-Hermitian positive semidefinite linear systems by use of the accelerated Hermitian and skew-Hermitian splitting iteration methods. According to theoretical analysis, we prove that all eigenvalues of the preconditioned matrices are very clustered with any positive iteration parameters α and β; especially, when the iteration parameters α and β approximate to 1, all eigenvalues approach 1. We also prove that the real parts of all eigenvalues of the preconditioned matrices are positive, i.e., the preconditioned matrix is positive stable. Numerical experiments show the correctness and feasibility of the theoretical analysis.

Mathematical subject classification: 65F10, 65N22, 65F50.

Key words: PAHSS, generalized saddle point problem, splitting iteration method, positive stable.

1 Introduction

Let us first consider the nonsingular saddle point system Ax = b as follows:

where, B ∈ C^n×n is Hermitian positive definite, D ∈ C^m×m is Hermitian positive semidefinite, E ∈ C^n×m (n ≥ m) has full column rank, ƒ ∈ Cⁿ, g ∈ C^m, and E^* denotes the conjugate transpose of E.

We review the Hermitian and skew-Hermitian splitting:

A = H + S,

where

Obviously, H is a Hermitian positive semidefinite matrix, and S is a skew-Hermitian matrix, see [1].

To solve the linear system (1), we have usually used efficient splittings of the coefficient matrix A. Many studies have shown that the Hermitian and skew-Hermitian splitting (HSS) iteration method is very efficient, see e.g., [1-15].In particular, Benzi and Golub [2] considered the HSS iteration method and pointed out that it converges unconditionally to the unique solution of the saddle point linear system (1) for any iteration parameter. In the case of D = 0, Bai et al. [3] proposed the PHSS iteration method and showed the advantages of the PHSS iteration method over the HSS iteration method by solving the Stokes problem. Bai et al. [4] generalized the PHSS iteration method by introducing two iteration parameters and proved theoretically the convergence rate of the obtained AHSS iterative method is faster than that of the PHSS iteration method, when they are applied to solve the saddle point problems. Under the condition that B is symmetric and positive definite and D = 0, Simoncini and Benzi [5] estimated bounds on the spectral radius of the preconditioned matrix of the HSS iteration method and pointed out that any eigenvalue (denote by λ) of the preconditioned matrix approximates to 0 or 2, i.e., λ ∈ (0, ε₁)∪ (ε₂, 2), with ε₁, ε₂ > 0 and ε₁, ε₂→ 0, as α → 0; meanwhile, they pointed out that all eigenvalues are real while the iteration parameter α ≤λ_n, where λ_n is the smallest eigenvalue of B; Bychenkov [6] obtained more accurate result than that in [5] and believed that all eigenvalues are real, as the iteration parameter α ≤ λ_n. Chan, Ng and Tsing [7] studied the spectral analysis of the preconditioned matrix of the HSS iteration method for the generalized saddle point problem for the case of D = µI_m, researched the spectral properties of the preconditioned matrices,and gave sufficient conditions that all eigenvalues of the preconditioned matrix are real. Huang, Wu and Li [8] studied the spectral properties of the preconditioned matrix of the HSS iteration method for nonsymmetric generalized saddle problems and pointed out that the eigenvalues of the preconditioned matrixgather to (0,0) or (2,0) on the complex plane as the iteration parameter approaches 0. Benzi [9] presented a generalized HSS (GHSS) iteration method by splitting H into the sum of two Hermitian positive semidefinite matrices.

In [1, 2], the following Hermitian and skew-Hermitian splitting iteration method was used to solve the large sparse non-Hermitian positive semidefinite linear system (1) with D = 0:

where α is a given positive constant and I_n+m is the identity matrix of order n+m. The equation (3) can be rewritten as

x^k+1 = M(α)x^k + N(α)b,

where

M(α) = (αI_n+m + S)^-1 (αI_n+m - H) (αI_n+m + H)^-1 (αI_n+m - S),

N(α) = 2α(αI_n+m + S)^-1 (αI_n+m + H)^-1.

By simple manipulation, the authors of [1, 2] obtained the preconditioner of the following form

P(α) = [N(α)]^-1 = (2α)^-1 (αI_n+m + S)(αI_n+m + H)

According to theoretical analysis, they proved the spectral radius ρ(M(α)) < 1 and the optimal iteration parameter

where γ_min, γ_max and λ denote the minimum, the maximum and the arbitrary eigenvalue of H, respectively.

We review the accelerated Hermitian and skew-Hermitian splitting (AHSS) iteration method established in [4] and first consider the simpler case that D = 0. Let U ∈ C^n×n be nonsingular such that U^*BU = I_n, and V ∈ C^m×m be also nonsingular. We denote by

Then, the linear system (1) is equivalent to

where

with

Therefore, the AHSS iteration method proposed in [4] can be written as follows:

where

with α and β are any positive constants.

Further, by straightforward computation, it is easy to see that

A = M(α, β) - N(α, β) and = (α, β)- (α, β),

where

and

Now we consider the general case that D ≠ 0, Bai and Golub in [4] further extended the AHSS iteration method to solve the generalized saddle point problems and proposed the AHSS preconditioner of the following form

In this paper, we use the AHSS iteration method to solve the generalized saddle point system (1) with D being positive semidefinite. According to the analysis, we easily know that the preconditioner proposed in this paper is different from the AHSS preconditioner in (5). We prove that all eigenvalues of the preconditioned matrices are very clustered with any positive iteration parameters α and β; especially when the iteration parameters α and β approximate to 1, all eigenvalues approach 1. We also prove that the real parts of all eigenvalues of the preconditioned matrix are positive, i.e., the preconditioned matrix is positive stable. Numerical experiments show the correctness and feasibility of the theoretical analysis.

2 Spectral analysis for PAHSS iteration method

Bai [16] studied algebraic properties of the AHSS iteration method for solving the general saddle point problem (1) when D = 0 and obtained the optimal parameters. By theoretical analysis and numerical experiments, we easily see that the AHSS iteration method is considerably robust and efficient. For the large sparse generalized saddle-point problems, Bai in [17] only introduced the AHSS iteration methods and the AHSS preconditioner in (5). In this paper, we propose a preconditioner based on the AHSS iteration method, called the preconditioned AHSS (PAHSS) preconditioner, which is different from the AHSS preconditioner in (5), and study in detail the related spectral properties of the PAHSS iteration method. So, the study in this paper is a complement and an extention of that in [17]. In this section, our main contribution is to use the PAHSS iteration method to solve the generalized saddle point problem (1) when D is positive semidefinite and to analyze the spectral properties of the preconditioned matrix. First, we consider the special case that D is a Hermitian positive definite matrix, and we begin our analysis by giving some notations.

Assume that UB E (D )^*V^* = Σ is the singular value decomposition [17, 18], both U ∈ C^n×n and V ∈ C^m×m are unitary matrices, where B = B

B₁, D = D

D₁ and

Σ₁ = Σ = diag{σ₁, σ₂,..., σ_m} ∈ C^m×m,

where σ_i (i = 1, 2,..., m) denote the singular values of B E (D)^*.

We apply the following preconditioned AHSS iteration method to solve the generalized saddle point system (1),

where H and S are defined as in (2), and

with α and β being any positive constants. When the iterative parameter α = β, we can easily know that the iteration method (6) reduces to the PHSS iteration method [3]. Bai, Golub and Li proposed in [19] the preconditioned HSS iteration method. When we properly select the matrix P or the parameter matrix in [19], we easily know the AHSS iteration method is a special case of that in [19].

By simple calculation, the iteration scheme (6) can be equivalently written as

where

Φ(α, β) = (Λ + S)-1 (Λ - H)(Λ + H)-1(Λ - S)

Ψ(α, β) = 2(Λ + S)-1 (Λ + H)-1 .

After straightforward operations, we obtain the following preconditioner

It is straightforward to show that

A = M(α, β) - N(α, β),

where

In the following, we denote by

Then, we obtain the following two equalities:

According to (9), we further get

where

Subsequently, by analysing the eigenproblem

we obtain the following related properties for the eigenvalues λ of the iteration matrix [M(α, β)]-1 N(α, β).

Theorem 2.1. Consider the linear system (1), let B and D be Hermitian positive definite matrices, E ∈ C^n×m have full column rank, and α, β be positive constants. If σ_k (k = 1,2,...,m) are the singular values of the matrix BE(D)^*, where B = BB₁, and D = DD₁, then the eigenvalues of the iteration matrix [M(α, β)]^-1N(α, β) of the PAHSS iteration method are with multiplicity n - m, and, for k = 1,2,...,m, the remainder eigenvalues are

Proof. Equivalently, the eigenvalue problem (12) can be written as the following generalized eigenvalue problem:

Then, according to (8) we obtain

T*N (α, β) TT^-1x = λT*M(α, β) TT^-1x.

Therefore, according to the formulas (9) and (10), the generalized eigenvalue problem (13) is equivalent to

(α, β) = λ(α, β),

where

i.e.,

[(α, β)]^-1 (α, β) = λ,

By straightforward computation, we see that

where

For the convenience of our statements, we denote by

By [17, Lemma 2.6], we obtain the kth (k = 1,2,..., m) block submatrix of (α, β):

where

We denote by 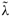an arbitrary eigenvalue of Θ(α, β)_k. Then it holds that

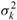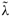² - 2 (αβ - 1) (αβ - ) + (α² - 1)(β² - 1)(αβ + 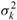)² = 0.

Further, for k = 1,2,...,m, we have

Therefore, we complete the proof of Theorem 2.1.

Theorem 2.2.

Let the conditions of Theorem 2.1 be satisfied. Then all eigenvalues of [M(α,β)]^-1N(α,β) are real, provided α and β meet one of the following cases:

i) α < 1, β > 1 or α > 1, β < 1;

ii) α = 1, β ≠ 1 or β = 1, α ≠ 1;

iii) 0 < α, β < 1 or α, β > 1, α ≠ β, and σ_k < σ_-, or σ_k > σ₊, k = 1,2,...,m,

where σ_- and σ₊ are the roots of the quadratic equation:

|α - β|σ²-2|αβ-1|σ + αβ|α - β| = 0,

with

Proof. According to (15), we obtain that 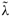k_± (k = 1,2,...,m) are all real if and only if

(α - β)² (αβ + 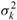)² - 4αβ 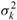(αβ - 1)²≥ 0,

i.e.,

|α - β|(αβ+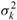) ≥ 2σ_k|αβ-1|.

Further, we have

|α - β|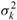 - 2|αβ - 1|σ_k + αβ|α - β| ≥ 0.

Consider the following inequality

On one hand, if α and β satisfy the conditions i) and ii), then

4αβ(α - 1)²- 4αβ(α - β)² = 4αβ(α² - 1)(β² - 1) ≤ 0.

It is easy to obtain the inequality (16). On the other hand, if 0 < α, β < 1 or α, β > 1 and α ≠ β, then we have

4αβ(αβ - 1)²- 4αβ(α - β)² = 4αβ(α² - 1)(β² - 1) > 0.

So, for all σ_k (k = 1,2,...,m), we can find out some positive constants α and β such that σ_k < σ_-, or σ_k > σ₊. Then, the inequality (16) is obtained.

Hence, as α and β meet one of the cases i), ii) and iii), we obtain 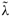k_± (k = 1,2,...,m) are all real, i.e., λk_± = (k = 1,2,..., m) are all real.

So, we complete the proof of Theorem 2.2.

Theorem 2.3.

Let the conditions of Theorem 2.1 be satisfied. Denote byρ_PAHSS the spectral radius of the iteration matrices [M(α, β)]^-1N(α, β). Then, we have

1) if the iteration parameters α and α satisfy one of the following conditions

i) α > β ≥ 1,

ii) α < β ≤ 1,

iii) β > 1, α < 1, and αβ ≤ 1,

iv) β < 1, α > 1, and αβ ≥ 1,

v) α = β ≠ 1,

then, ρ_PAHSS =

2) if the iteration parameters α and β satisfy one of the following conditions

i) β > α ≥ 1,

ii) β < α ≤ 1,

iii) β > 1, α < 1, and αβ > 1,

iv) β < 1, α > 1, and αβ < 1,

then, ρ_PAHSS≤

Proof. In order to complete the above proves, we first estimate the bounds of 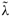and λ ( 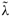and λ defined as in Theorem 2.1). As one of the conditions i), ii) or iii) in Theorem 2.2 are satisfied, then, we easily obtain the following result

Further, we obtain

If 0 < α, β < 1, or α, β > 1, and σ_k ∈ [σ_-, σ₊],(k = 1, 2,..., m), (σ_-, σ₊ defined as in Theorem 2.2), it is obvious that

Further, we have

Secondly, since ƒ₁(x) = (x > 1) and ƒ₂(x) = (0 < x < 1) are monotone increasing function and monotone decreasing function, respectively, then

and

According to Theorem 2.1, the iteration matrices [M(α, β)]^-1 N(α, β) have n - m eigenvalues . Then, for any other eigenvalues of the iteration matrices, we complete the proves of the conclusions in 1) by the following four cases:

(i) If α > β ≥ 1, then, by (17), we obtain

and by (18), we have

(ii) If α < β ≤ 1, then, by (17), we have

and by (18), we get

(iii) If β > 1, α < 1, and αβ ≤ 1, or β < 1, α > 1, and αβ > 1, by (17), the inequality (21) can be straightforwardly obtained.

(iv) If α = β ≠ 1, according to (18), we have

Therefore, combining the above proves, we obtain

ρ_PAHSS = .

It is similar to prove the conclusion in 2). Therefore, we complete theproves.

Corollary 2.1. Let the conditions of Theorem 2.1 be satisfied.ρ_PAHSS defined as in Theorem 2.3. To solve the generalized saddle point problem (1), the PAHSS method unconditionally converges to the unique solution for any positive iteration parametersαandβ, i.e.,

ρ_PAHSS < 1.

Proof. According to Theorem 2.3, we straightforwardly obtain the above result.

Remark 2.1. According to Theorem 2.3, on the one hand, as the iteration parameters α and β approach 1, the spectral radius ρ_PAHSS approximates to 0, on the other hand, when the iteration parameter α is fixed, for different value β, we have

ρPAHSS_min = ,

where we denote by ρ_PAHSSmin the smallest spectral radius of the iteration matrix [M(α, β)]^-1 N(α, β) with different value β.

In the following, we study the spectral properties of the preconditioned matrix. Since

M(α, β)^-1 A(α, β) = I - M(α, β)^-1 N(α, β),

then

λ[M(α, β)^-1 A(α, β)] = 1 - λ[M(α, β)^-1 N(α, β)], (see e.g., [3])

Thus

with multiplicity n - m, the remainder eigenvalues of the preconditioned matrices are

where

For the convenience of our statements, we denote

and

According to the above analysis, we obtain the following results:

To generalized saddle point problem (1), Bai [16] proved the preconditioned matrix [M(α, β)]^-1A is positive stable (cf. [20] for the definition of positive stable matrix). In the following, we also obtain the same property.

Theorem 2.4. Let the conditions of Theorem 2.1 be satisfied. Then, for any positive constants a and b, the real parts of 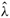k_- and 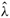k₊ (k = 1,2,..., m) are all positive, i.e., the preconditioned matrices [M(α, β)]^-1 A(α, β) are positive stable.

Proof. Obviously, is positive real. Denote by Re(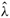) the real part o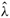f , if

0 < α, β < 1 or α, β > 1 and α ≠ β, for any k = 1, 2,..., m, σ_k∈ [σ_-, σ₊],

then according to (23) or (24), we get

Re(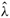) ≥ 0.

If a and b meet one of the cases i), ii) or iii) in Theorem 2.2, then, we have

(α - β)²(αβ + 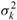)²- 4αβ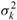(αβ - 1)²≥ 0.

Thus

Re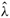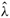(k_± ) = k_±.

Obviously

Re(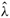k₊ ) ≥ 0.

According to (24), we obtain

i.e.,

Re(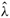k_{_} ) ≥ 0.

Therefore, we complete the proof of Theorem 2.5.

Theorem 2.5.

Let

k₊, and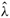 k_{_} defined as in (23) and (24), respectively. Then, we obtain the following properties of the eigenvalues of the preconditioned matrices M(α, β)^-1A(α, β)

1) As the iteration parameters α and β approximate to 1, all eigenvalues of the preconditioned matrices M(α, β)^-1 A(α, β) approach 1.

2) For any positive iteration parameters α and β, the moduluses of all eigenvalues of the preconditioned matrices M(α, β)^-1 A(α, β) cluster in the interval (0,2).

Proof. According to Theorem 2.3 and Theorem 2.4, we can easily obtain the above results.

Further, we consider the general case with D being Hermitian positive semidefinite, then, we generalize our conclusions by taking steps similar to those taken in [3, Theorem 5.1]. Denote the Moore-Penrose generalized inverse of B₁ and D₁ by B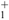and D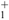, respectively, and the positive singular values of the matrix B

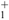E(D)^* by σ_i (i = 1, 2,..., m). By the similar analysis, we can obtained the similar results with the above spectral properties.

3 Numerical examples

In this section, we use two examples to illustrate the feasibility and effectiveness of the PAHSS iteration method for the generalized saddle point problems. We perform the numerical examples by using MATLAB with machine precision 10^-16 and using

║r_k║₂/║r₀║₂ = ║b - Ax^(k)║₂/║b║₂ < 10^-6

as a stopping criterion, where r_k is the residual at the kth iterate. Bai, Golub and Pan [3] considered the Stokes problem:

where Ω = (0, 1) × (0, 1) ⊂ R², ∂Ω is the boundary of Ω, Δ is the componentwise Laplace operator, u is a vector-valued function representing the velocity, and w is a scalar function represeting the pressure. By discretizing the above equation, linear system (1) be obtained with A ∈ R(3m²)×(3m²) and D = 0.

Example 1 [3]. Consider the following linear system:

where

and

in this example, we assume

D = (I ⊗ T + T ⊗ I) e Rm² x m²

where h = is the discretization meshsize, ⊗ is the Kronecker product symbol. Then, we confirm the correctness and accuracy of our theoretical analysis by solving the generalized saddle problem.

Example 2 [12]. Consider the following linear system:

where W = (w_k,j) ∈ R^q×q, N = (n_k,j) ∈ R^n-q×n-q, F = (f_k,j) ∈ R^(n-q)×q and 2q > n, where

In Figures 1, 2, ⁴ and ⁵, for different iteration parameters α and β, we depict the distribution on the eigenvalues of the preconditioned matrices [(α, β)]^-1. From these images, we see that the eigenvalues l of the preconditioned matrix are quite clustered.

In Tables 1 and 2, we can know that the smallest real part Re(λ)_min of the eigenvalues of the preconditioned matrix [(α, β)]^-1 are all positive, as the iteration parameters α and β take different values. Further, we know that the real parts of all eigenvalues of the preconditioned matrices are all positive, therefore, we numerically verify the accuracy of the Theorem 2.4.

In Figures 3 and ⁶, we plot the curves of the spectral radius denote by ρ_PAHSS, and with the change of β. From subfigure a, we know that ρ_PAHSS≤ , as β ∈ [0.1,0.5], ρ_PAHSS = , as β ∈ [0.5,2], and ρ_PAHSS ≤ , as β ∈ [2,4], From subfigure b, we know that ρ_PAHSS≤ , as β ∈ [0.1,0.4], ρ_PAHSS = , as β ∈ [0.4,2.5], and ρ_PAHSS≤ , as β ∈ [2.5,4]. Therefore, through the two images, we verify the efficiency and accuracy of Theorem 2.3.

In Tables 3 and 4, by using GMRES(l) (l = 5,10,20,100) iterative methods with PAHSS preconditioning, we compare between the preconditioner proposed in this paper and the preconditioner in (5) by the iteration numbers (denote by "IT") and the solution of times in seconds (denote by "CPU"). From the two tables, we can easily see that the superiority of the PAHSS iteration method is very evident.

Acknowledgements. The authors are grateful to the referee and associate editor Prof. M. Raydan who made much useful and detailed suggestions that helped us to improve the quality of the paper, especially in English grammar. This research was supported by NSFC (10926190, 60973015), Specialized Research Fund for the Doctoral Program of Higher Education (20070614001), Sichuan Province Sci. & Tech. Research Project (2009HH0025).

Received: 13/XI/09.

Accepted: 17/II/10.

#CAM-154/09.

• [1] Z.-Z. Bai, G.H. Golub and M.K. Ng, Hermitian and skew-Hermitian splitting methods for non-Hermitian positive definite linear systems. SIAM J. Matrix. Anal. Appl., 24 (2003), 603-626.
• [2] M. Benzi and G.H. Golub, A preconditioner for generalized saddle point problems. SIAM J. Matrix Anal. Appl., 26 (2004), 20-41.
• [3] Z.-Z. Bai, G.H. Golub and J.-Y. Pan, Preconditioned Hermitian and skew-Hermitian splitting methods for non-Hermitian positive semidefinite linear systems. Numer. Math., 98 (2004), 1-32.
• [4] Z.-Z. Bai and G.-H. Golub, Accelerated Hermitian and skew-Hermitian splitting iteration methods for saddle point problems. IMA J. Numer. Anal., 27 (2007), 1-23.
• [5] V. Simoncini and M. Benzi, Spectral properties of the Hermitian and skew-Hermitian splitting preconditioner for saddle point problems. SIAM J. Matrix Anal. Appl., 26 (2004), 377-389.
• [6] Yu.V. Bychenkov, Preconditioning of saddle point problems by the method of Hermitian and skew-Hermitian splitting iterations. Comput. Math. Math. Phys., 49 (2009), 411-421.
• [7] L.-C. Chan, M.K. Ng and N.-K. Tsing, Spectral analysis for HSS preconditioners. Numer. Math-Theory, Methods Appl., 1 (2008), 57-77.
• [8] T.-Z. Huang, S.-L. Wu, C.-X. Li, The spectral properties of the Hermitian and skew-Hermitian splitting preconditioner for generalized saddle point problems. J. Comput. Appl. Math., 229 (2009), 37-46.
• [9] M. Benzi, A generalization of the Hermitian and skew-Hermitian splitting iteration. SIAM J. Matrix Anal. Appl., 31 (2009), 360-374.
• [10] M. Benzi, M.J. Gander and G.H. Golub, Optimization of the Hermitian and skew-Hermitian splitting iteration for saddle-point problems. BIT, 43 (2003), 881-900.
• [11] Z.-Z. Bai, G.H. Golub and M.K. Ng, On successive-overrelaxation acceleration of the Hermitian and skew-Hermitian splitting iterations. Numer. Linear Algebra Appl., 14 (2007), 319-335.
• [12] Z.-Z. Bai, G.H. Golub, L.-Z. Lu and J.-F. Yin, Block triangular and skew-Hermitian splitting methods for positive-definite linear systems. SIAM J. Sci. Comput., 26 (2005), 844-863.
• [13] D. Bertaccini, G.H. Golub, S.S. Capizzano and C.T. Possio, Preconditioned HSS methods for the solution of non-Hermitian positive definite linear systems and applications to the discrete convection-diffusion equation. Numer. Math., 99 (2005), 441-484.
• [14] Z.-Z. Bai, G.H. Golub and C.K. Li, Optimal parameter in Hermitian and skew-Hermitian splitting method for certain two-by-two block matrices. SIAM J. Sci. Comput., 28 (2006), 583-603.
• [15] Y.V. Bychenkov, Optimization of the generalized method of Hermitian and skew-Hermitian splitting iterations for solving symmetric saddle-point problems. Comput. Math. Math. Phys., 46 (2006), 937-948.
• [16] Z.-Z. Bai, Optimal parameters in the HSS-like methods for saddle-point problems. Numer. Linear Algebra Appl., 16 (2009), 431-516.
• [17] G.H. Golub and C. Greif, On solving block-structured indefinite linear systems. SIAM J. Sci. Comput., 24 (2003), 2076-2092.
• [18] G.H. Golub and C.F. Van Loan, Matrix Computations. 3rd Edition, The Johns Hopkins University Press, Baltimore (1996).
• [19] Z.-Z. Bai, G.H. Golub and C.-K. Li, Convergence properties of preconditioned Hermitian and skew-Hermitian splitting methods for non-Hermitian positive semidefinite matrices. Math. Comput., 76 (2007), 287-298.
• [20] R.A. Horn and C.R. Johnson, Topics in Matrix Analysis. Cambridge University Press, Cambridge (1991).
• [21] M. Eiermann, W. Niethammer and R.S. Varga, Acceleration of relaxation methods for non-Hermitian linear systems. SIAM J. Matrix Anal. Appl., 13 (1992), 979-991.

Publication Dates

• Publication in this collection
  22 July 2010
• Date of issue
  June 2010

History

• Received
  13 June 2009
• Accepted
  17 Feb 2010