Application of interval analysis for gibbs and helmholtz free energy global minimization in phase stability analysis

THERMODYNAMICS

Application of interval analysis for gibbs and helmholtz free energy global minimization in phase stability analysis

A. T. Souza^I; L. Cardozo-FilhoII, ^*; F. Wolff^II; R. Guirardello^I

^IFaculdade de Engenharia Química, UNICAMP/FEQ/DPQ, 13081-970, Campinas - SP, Brazil, E-mail: [e-mail]

^IIDepartamento de Engenharia Química, UEM/DEQ 87020-900, Maringá - PR - Brazil E-mail:[e-mail]

ABSTRACT

The tangent plane criterion has become important for a correct solution evaluation phase and chemical of equilibrium problem. This method, applicable to single and multiphase systems, is mainly used for a single equation of state modeling all phases involved. The present work is mainly concerned with the application of interval analysis methods for global energy minimization in high-pressure phase stability problems. Two approaches are applied: (i) the Gibbs free energy global minimization under conditions of constant temperature and pressure and (ii) the Helmholtz free energy density global minimization under conditions of constant temperature and volume. Five case studies, one ternary and four binary systems, are analyzed in connection with the Peng-Robinson equation of state (PREOS) model. Five more case studies, for the CO₂ + trans-2-hexen-1-ol system at high pressures, are used to compare different methods of phase equilibrium calculation with the approach using interval analysis. Finally, a complex system, clove oil + CO₂, is analyzed. The results indicate that the interval analysis method is robust and reliable for all the problems studied.

Keywords: Phase stability; Interval analysis; Mathematical modeling, Gibbs free energy; Helmholtz free energy.

INTRODUCTION

Nonreactive Phase Stability

Stability analysis of an admissible state is illustratively described in terms of behavior of the system when submitted to perturbations. Depending on this behavior, the state is usually defined as stable, metastable, or unstable equilibrium. In what follows, the main interest is to verify whether or not an admissible state is stable.

The stable equilibrium criterion for closed systems is a well-established result in thermodynamics and may be presented in several equivalent forms. In nonreactive phase stability analysis, much attention has been given to the criterion in terms of the Gibbs free energy, G (Michelsen, 1982a,b; Sun and Seider, 1995; McKinnon, et al., 1996; Wasylkiewicz, et al., 1996; McDonald and Floudas, 1997; Hua, et al., 1997), and in terms of the Helmholtz free energy density, Ã (Nagarajan and Cullick, 1991; Xu, 2001; Xu et al., 2002).

Phase Stability Analysis Using the Gibbs Free Energy

The equilibrium criterion in terms of the Gibbs free energy can be expressed as follows: the stable equilibrium state of a closed system with given internal constraints at constant T = T₀ and P = P₀ is characterized by a global minimum of G with regard to all equilibrium states compatible with the fixed values of T₀ and P₀ and the given internal constraints (Callen, 1985; Tester and Modell, 1997).

When applied to a nonreactive single-phase and closed simple system at constant T₀ and P₀, this criterion requires that no admissible two-phase configuration have a value for G value smaller than , the original value. If G < G₀ for any two-phase configuration, then the state under study is not stable.

Suppose that an arbitrarily small perturbation converts the single-phase system into a two-phase system. At constant T₀ and P₀, the following simplified notation will be used: Thus, the variation in the Gibbs free energy for the above change of state can be represented by

A Taylor expansion of G^I in becomes

where is the chemical potential of species i in the original phase and y_i is the molar fraction of species i in the new phase. In the above expansion, use was made of

and

Substituting (2) and (3) into (1) gives

For sufficiently small e and taking into account that e > 0, the sign of DG in (4) is given by the sign of

Therefore a necessary and sufficient condition for a phase to be in stable equilibrium is that for any composition .

Phase Stability Analysis Using the Helmholtz Free Energy

The equilibrium criterion in terms of the Helmholtz free energy can be expressed as follows: the stable equilibrium state of a closed system with given internal constraints at constant T = T₀ and V = V₀ is characterized by a global minimum of A with regard to all equilibrium states compatible with the fixed values of T₀ and V₀ and the given internal constraints (Callen, 1985; Tester and Modell, 1997).

This criterion, when applied to a nonreactive single-phase system, requires that no admissible two-phase configuration have a value for A smaller than , the original value. If A < A₀ for any two-phase configuration, then the state studied is not stable.

Suppose that an arbitrarily small perturbation converts the single-phase system into a two-phase system. At constant T₀, the following simplified notation will be used: Thus, variation in the Helmholtz free energy for the above change of state can be represented by

A Taylor expansion of A^I in becomes

where is the chemical potential of species i in the original phase and V and y_i are the molar volume and molar fraction of species i in the new phase. In the above expansion, use was made of

and

where

Substituting (7) and (8) into (6) gives:

For sufficiently small e and taking into account that e > 0, the sign of DA in (9) is given by the sign of

Therefore, a necessary and sufficient condition for a phase to be in stable equilibrium is that for any molar volume V and any composition .

Nagarajan and Cullick (1991) developed an alternative criterion involving the Helmholtz free energy for a unit volume (Helmholtz free energy density, Ã), for a system with constant T and P. Using the following species molar densities

it can be observed that the Helmholtz free energy density at a given temperature can be represented by a function:

It can be readily shown that µ_i and P can also be expressed as functions:

Combining (10) and (13) allows to be expressed as a function:

Therefore, a necessary and sufficient condition for a phase to be in stable equilibrium is that for any acceptable value of .

The advantage of using this last approach is that the function à versus is smooth, while G versus is not always a smooth function.

Mathematical Modeling

In order to verify whether for all admissible variable values, it is sufficient to test these criteria at the stationary points of or For the Helmholtz free energy density approach, the stationary points satisfy the following equation:

Determination of the stationary point coordinates corresponds to finding all the roots of the nonlinear equation given by (15). A reliable and robust method for this is given by the interval for the Newton/generalized bisection algorithm, based on interval analysis and interval arithmetic (Stadtherr, et al., 1995; Kearfott, 1996). The main advantage of this method is that it finds with certainty all the roots of the nonlinear set of equations, proving that each solution is enclosed within some bounds. The main drawback is that, depending on the nature of the problem a long computational time may be required to achieve this certainty.

In this work, the interval Newton/generalized bisection algorithm was used in connection with the Peng-Robinson equation of state (PREOS) model to solve the stability problems, using the Van der Walls mixing rules. The INTBIS and INTLIB softwares were used for the numerical calculations of the roots (Kearfott and Novoa, 1990; Kearfott et al., 1994).

NUMERICAL RESULTS

Five stability analysis sample problems and their respective computational results using the Helmholtz free energy density formulation are given below. The results for each case include the stationary point coordinates and the corresponding values. The same problems were studied by Hua et al. (1997, 1998) with the Gibbs free energy approach. The corresponding results will not be reproduced here and can be found in the above - cited references. With respect to the computational time required to solve the problems, it was observed that the approach based on the Helmholtz free energy density required roughly less than half of the time needed by the approach based on the Gibbs free energy, using the same machine and software.

Problem 1. Hydrogen sulfide (1) + Methane (2)

This is a binary mixture of H₂S (1) and CH₄ (2) at 190 K and 40.35 bar. The PREOS model was used with parameters calculated from T_c1=373.2 K, P_c1=89.4 bar, w₁=0.1, T_c2=190.6 K, P_c2=46.0 bar, w₂=0.008, and the binary interaction parameter k₁₂=0.08. Six original compositions were considered, with results shown in Table 1.

Problem 2. Methane (1) + Propane (2)

This is a binary mixture of CH₄ (1) and C₃H₈ (2) at 277.6 K and 50 bar. The PREOS model was used with parameters calculated from methane data given above, T_c2=369.8 K, P_c2=42.5 bar, w₂=0.152, and the binary interaction parameter k₁₂=0.029. Four original compositions were considered, with results shown in Table 2.

Problem 3. Nitrogen (1) + Ethane (2)

This is a binary mixture of N₂ (1) and C₂H₆ (2) at 270 K and 76 bar. The PREOS model was used with parameters calculated from T_c1=126.2 K, P_c1=33.9 bar, w₁=0.04, T_c2=305.4 K, P_c2=48.8 bar, w₂=0.098, and the binary interaction parameter k₁₂=0.08. Four original compositions were considered, with results shown in Table 3.

Problem 4. Carbon dioxide (1) + Methane (2)

This is a binary mixture of CO₂ (1) and CH₄ (2) at 220 K and 60.8 bar. The PREOS model was used with parameters calculated from T_c1=304.2 K, P_c1=73.8 bar, w₁=0.225, the methane parameters given above, and the binary interaction parameter k₁₂=0.095. Four original compositions were considered, with results shown in Table 4.

Problem 5. Nitrogen (1) + Methane (2) and Ethane (3)

This is a ternary mixture of N₂ (1), CH₄ (2) and C₂H₆ (3) at 270 K and 76 bar. The PREOS model was used with T_c1=126.2 K, P_c1=33.9 bar, w₁=0.04, T_c2=190.6 K, P_c2=46.0 bar, w₂=0.008, T_c3=305.4 K, P_c3=48.8 bar, w₃=0.098, and binary interaction parameters k₁₂=0.038, k₁₃=0.08, and k₂₃=0.021. Four original compositions were considered, with results shown in Table 5.

COMPARING DIFFERENT APPROACHES

In order to show the advantages of using the interval analysis method, a number of different methods in the literature were compared, using as example the CO₂ + trans-2-Hexen-1-ol system at high pressures, whose phase behave is known to be difficult to model (Stradi et al., 2001a,b). Table 6 shows the results for the molar fractions (x_CO2 and x_CO2) for different methods used to calculate the flash equilibrium. The case studies are the same as those presented in Stradi et al. (2001a,b), where P1, P2, and P3 are the methods used by those authors, and M1 is the approach used in this paper with interval analysis.

In case study 1, the same results were found with conventional methods P1, P2 and P3, but all were incorrect. In case study 2, using P1, P2, and P3 it was incorrectly found that there would be no phase splitting. In these two cases, the pressure was close to the point of the three-phase line, therefore presenting numerical difficulties that caused these methods to fail. These difficulties were avoided with the approach used in this paper, M1, which resulted in consistently reliable results.

For case studies 3, 4, and 5, it can be observed that methods P1, P2, and P3 failed once for the flash calculations. P3 failed in case study 4 by not predicting the phase splitting. P2 failed in case study 5 by not predicting the phase splitting. In case study 3, P1 correctly predicted the phase split, but it resulted in numerical errors and was not able to find the solution. All these difficulties are very common in conventional methods used to model phase equilibrium. Again, the approach used here was able to find the correct solutions in all cases.

EQUILIBRIUM ANALYSIS FOR A COMPLEX SYSTEM

The approach used in this paper was applied to describe the phase equilibrium behavior of the clove oil + CO₂ system, using experimental data from Souza et al. (2004). The main characteristic of this system, formed of an essential oil and carbon dioxide, is the large variety of different types of chemical groups found in the essential oil, which is in fact a complex system.

The calculations were done at two temperatures, 303.15 K and 308.15 K, and the model predicted a three-phase line at pressures of 71.25 and 80.15 bar, respectively. Above these pressures there is a liquid-liquid phase region, and below these pressures there is a liquid-vapor phase region. This can be observed in Figures 1a and 1b. It can be seen that the model was able to fit the experimental data for the clove oil + CO₂ system reasonably well. The values for the fitted parameters (k₁₂, l₁₂) as well as the critical properties and the accentric factors were determined by Souza et al. (2004).

CONCLUSIONS

The foregoing results show that interval analysis provides a reliable method for solving phase stability problems with the Gibbs or Helmholtz free energy approach. However, higher convergence speeds are obtained with the Helmholtz free energy density formulation than with the Gibbs free energy formulation. This is probably due to the smooth behavior of the Helmholtz energy density function, as pointed out by Nagarajan and Cullick (1991). The method is general purpose and can be applied in connection with other EOS models, such as the SAFT EOS model (Xu et al., 2002).

ACKNOWLEDGMENTS

We gratefully acknowledge the financial support received for this research from FAPESP process number 00/02566-1.

NOMENCLATURE

A Helmholtz free energy A^I Helmholtz free energy in phase I A^II Helmholtz free energy in phase II Ã(r)

Helmholtz energy density surface

D

tangent plane distance

G Gibbs free energy G^I Gibbs free energy in phase I G^II Gibbs free energy in phase II k_ij binary interaction parameter of component i in phase j n number of moles N number of species P pressure P_c

critical pressure

R gas constant T temperature T_c critical temperature V volume V_e infinitesimal volume of phase formed molar volume y_i mole fraction of species I Z molar fraction of the feed e infinitesimal mole number of phase formed µ_i chemical potential of species I r_i molar density of species I w acentric factor Ñ gradient vector 0 used to indicate evaluation of feed composition

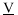
Received: October 15, 2003

Accepted: August 18, 2005

• Callen, H.B., Thermodynamics and an Introduction to Thermostatistics, 2nd Ed., Wiley, New York (1985).
• Hua, J.Z., Brennecke, J.F, and Stadtherr, M.A., Combined Local and Global Approach to Reliable Computation Phase Equilibria. Presented at AIChE Annual Meeting, Los Angeles, CA, 16-21 (1997).
• Hua, J.Z., Brennecke, J.F, and Stadtherr, M.A., Reliable Computation of Phase Stability using Interval Analysis: Cubic Equation of State Models. Computers & Chemical Engineering, 20, 1207 (1998).
• Kearfott, R.B., and Novoa, M., Algorithm 681: INTBIS - A Portable Interval Newton/Bisection Package. ACM Trans. Math. Software, 16 (2), 152-157 (1990).
• Kearfott, R.B., Dawande, M., Du, K.S., and Hu, C.Y., Algorithm 737: INTLIB - A Portable FORTRAN 77 Interval Standard Function Library. ACM Trans. Math. Software, 20 (4), 447-459 (1994).
• Kearfott, R.B., Rigorous Global Search: Continuous Problems, Kluwer Academic Publishers, Netherlands (1996).
• McDonald, C.M. and Floudas, C.A., GLOPEQ: A New Computational Tool for the Phase and Chemical Equilibrium Problem. Comput. Chem. Eng. 21, 1 (1997).
• McKinnon, K.I. M., Millar, C.G., and Mongeau, M., Global Optimization for the Chemical and Phase Equilibrium Problem using Interval Analysis. In: Floudas, C.A., Pardalos, P.M. (Eds.), State of the Art in Global Optimization: Computation Methods and Applications, 365-382 (1996).
• Michelsen, M.L., The Isothermal Flash Problem. Part I. Stability. Fluid Phase, 9, 1-19 (1982a).
• Michelsen, M.L., The Isothermal Flash Problem. Part II: Phase-split calculation. Fluid Phase Equilibria, 9, 21-40 (1982b).
• Nagarajan, N.R. and Cullick, A.S., New Strategy for Phase Equilibrium and Critical Point Calculation by Thermodynamic Energy Analysis. Part I. Stability Analysis and Flash. Fluid Phase, 62, 191-210 (1991).
• Souza, A.T. de; Corazza, M.L.; Cardozo-Filho, L.; Guirardello, R.; and Meireles, M.A. de A. Phase Equilibrium Measurements for the Systems Clove (Eugenia carophyllus) Oil + CO₂ Journal of Chemical and Engineering Data, USA, 49, 352-356 (2004).
• Stadtherr, M.A., Schnepper, C.A. and Brennecke, J.F., Robust Phase Stability Analysis Using Interval Method. AIChE Symposium Series, 91(304), 356-359 (1995).
• Stradi, B.A., Xu, G., Brennecke, J.F., and Stadtherr, M.A., Modeling and Design of an Environmentally Begun Reaction Process. Departament of Chemical Engineering, University of Notre Dame, IN 46556 (2001a).
• Stradi, B.A., Stadtherr, M.A., and Brennecke, J.F., Multicomponent Phase Equilibrium Measurements and Modeling for the Allylic Epoxidation of Trans-2-hexen-1-ol to (2R,3R)-(+)-propyloxiranemethanol in High Pressure with Carbon Dioxide, Journal of Supercritical Fluids, 20, 1-13 (2001b).
• Sun, A.S. and Seider, W.D., Homotopy-Continuation Method for Stability Analysis in the Global Minimization of Gibbs Free Energy. Fluid Phase Equilibria 103,213-249 (1995).
• Tester, J.W. and Modell, M., Thermodynamics and Its Applications, 3r Ed., Prentice Hall, USA (1997).
• Wasylkiewicz, S.K., Sridhar, L.N., Doherty, M.F. and Malone, M.F., Global Stability Analysis and Calculation of Liquid-Liquid Equilibrium in Multicomponent Mixtures. Ind. Eng. Chem. Res., 35, 1395-1408 (1996).
• Xu, G., Reliable Phase Stability and Equilibrium Calculation Using Interval Analysis for Equation of State Models. Ph.D. dissertation. University of Notre Dame, Notre Dame, Indiana (2001).
• Xu, G., Brennecke, J.F., and Stadtherr, M. A., Reliable Computation of Phase Stability and Equilibrium from the SAFT Equation of State, Ind. Eng. Chem. Res., 41, 938-952 (2002).

*

To whom correspondence should be adressed

Publication Dates

• Publication in this collection
  07 July 2006
• Date of issue
  Mar 2006

History

• Received
  15 Oct 2003
• Accepted
  18 Aug 2005