First principle calculation of potential and multi-channel transport in Fe/MgO/Fe hetero-junction

First principle calculation of potential and multi-channel transport in Fe/MgO/Fe hetero-junction

Sebastian Ujevic^*; J. A. Gómez^†; Ivan A. Larkin^‡

International Center of Condensed Matter Physics, University of Brasília, Brasília - Distrito Federal, 70904-970 Brazil

ABSTRACT

In this work we studied the behavior of multi-channel tunneling through a realistic Fe/MgO/Fe hetero-junction ab initio potential. For this purpose we obtained Fe/MgO/Fe(001) hetero-junction effective potentials using the full potential-linear augmented plane wave WIEN2k code together with the generalized gradient approximation for the exchange-correlation potential. Multi-channel tunneling through the Fe/MgO/Fe hetero-junction barrier was studied within a few modes model. The transfer matrix technique was used to calculate the transmission and reflection amplitudes between Bloch states in the semi-infinite leads. The transmission coefficients were used in Fisher and Lee formula for conductance, an expression derived from Kubo formula and valid for any number of scattering channels.

Keywords: Hetero-Junctions; Electronic Transport; S-Matrix Theory

I. INTRODUCTION

In recent years much effort was devoted in the understanding of the mechanisms of spin-dependent tunneling conductance between ferromagnetic electrodes separated by insulating oxide barrier. Most of the studies were addressed to the Fe/MgO/Fe(001) magnetic tunnel junctions (MTJ). Experimentally, the ability to deposit epitaxially [1-6] MgO over Fe-bcc and then another Fe electrode on top of MgO was able to demonstrate large values of tunnel magnetoresistance (TMR) of up to 220 per cent [7,8]. Even larger values of TMR were obtained for MTJ with Co electrodes of more that 400 per cent at room temperature [9]. The high values of TMR make these MTJs potential candidates for future high-density [10,11] and logic [12] device applications.

One of the goals of the present paper is to study the behavior of scattering wave functions in realistic ab initio potential. In this work we studied the behavior of multi-channel tunneling through Fe/MgO/Fe(001) hetero-junctions, however our methods are applicable to any tunneling multi-channel problem. To do that, we first obtained effective potentials by performing first-principle calculations on super-cells that simulate Fe/MgO/Fe(001) MTJ with the full-potential augmented plane waves (FP-LAPW) WIEN2k code [13]. Next, in order to calculate the conductance of the system, we used the wave function matching technique to calculate the transmission and reflection amplitudes between Bloch waves in the leads [14]. Then by separating incoming and outgoing waves we build up the scattering matrix S. The matrix elements of S provides all the necessary information to calculate conductance [15]. Contrary to [16] we have not calculated eigen-vectors of S as we can use for conductance the relation Tr (tt⁺) = .

The paper is organized as follows: in the next section the details and results of the Fe/MgO/Fe hetero-junction potential calculations are given. In Sec. III the mathematical general solution of the Schrodinger equation for the system is found and in Sec. IV the available physical solutions for the system, that corresponds to traveling or evanescent waves, are build. In Sec. V we shown the procedure employed to calculate the conductance through the hetero-junction. The conductance results for a two modes model within the Fe/MgO/Fe system are shown in Sec. VI. Finally in Sec. VII the conclusions are presented.

II. THE HETERO-JUNCTION POTENTIAL

We calculated the electronic structure of pure bulk α-Fe and MgO and also the magnetic hetero-junction α-Fe/MgO/α-Fe(001) with the FP-LAPW WIEN2k code within the framework of density functional theory [17,18]. We considered for the calculation of the hetero-junction a super-cell with 3 and 17 mono-layers of MgO and Fe respectively; we will labeled this super-cell as 9Fe/3MgO/8Fe(001). For the bulk elements calculations (Fe and MgO), the experimental lattice parameters were employed. For the 9Fe/3MgO/8Fe(001) hetero-junction calculations, we imposed the MgO mono-layers to have their in-plane lattice parameter slightly reduced in order to match with the Fe (bcc) interface. Furthermore the distance between MgO mono-layers have been increased to keep the volume of the conventional unit cell equal to the bulk MgO. In addition, we considered that Fe atoms sits atop the oxygen atoms on the interface. The distance between iron and oxygen atoms considered in our calculation was 2.16 Å.

After the electronic structure calculation for the hetero-junction was done, we analyzed how the MgO potential perturbed the Fe-bcc region inside the super-cell. It was seen that this perturbation decays quickly with a length of about 2 to 3 Fe layers near the Fe-MgO interface and from this point the potential behave like a periodic bulk iron. This quick decay of the perturbation is due to the small screening length of the Fe electrons (few Bohr distance). In this sense, the nFe/MgO/mFe super-cells with n and m 5 number of Fe layers will represent good MTJ for transport calculations.

The next step for the electronic structure calculations of the MTJs is to compare the averaged electron charge densities of Fe atoms at the edge sites of the super-cell that simulate the 9Fe/3MgO/8Fe(001) MTJ, with the charge density of the pure Fe bulk calculation and check that there are equal. Atomic positions of Fe at the edge of the MTJ must simulate properties of the bulk Fe like charge, potential density profiles and symmetry (cubic in this case), but in super-cells with a finite number of Fe layers there are not quantitatively the same. This will depend on the number of Fe layers used to describe the MTJs in the super-cell. In our 17 Fe layers MTJ calculation, we observed that the charge density profile of the most distant Fe layers are quite similar to the charge density of bulk Fe. We performed this comparison by checking the total electronic charges inside the muffin-tin (MT) radius for spin up and spin down populations. This is a good check because we chose as large as possible MT radius that approximately 96 percent of the electronic charge is inside the spheres, and at the interstitial region the charge density is near homogeneous and very similar to bulk Fe. From the calculation of neutral 9Fe/3MgO/8Fe(001) super-cell we found a slightly leakage of electronic charge of Fe (compared to bulk Fe) at the edge and next to the edge layers of less that 1 per cent. To adjust this electronic charge we performed a series of calculations in charged super-cells adding fractional electron charges until we reached quite similar electronic charges compared to bulk Fe with a difference of less than 0.1 per cent. The electronic valence charge of neutral 9Fe/3MgO/8Fe(001) super-cell is 286 electrons. A charged super-cell with +0.4 electron was needed to fill the MT spheres at the edge of the Fe layer with appropriate electronic charge.

The converged potential for bulk iron and 9Fe/3MgO/8Fe(001) hetero-junction were used in spin-dependent conductance calculations as described in the next sections. In this calculation, the bulk Fe potential obtained above was considered as the lead potential and two semi-infinite Fe crystals, representing the left and right sides of the 9Fe/3MgO/8F(001) hetero-structure, were built. Due to applications in the next sections, we need to calculate the Fourier components of the full-potential along the z axis. For this purpose we defined a 2D unit cell in the XY plane with periodic conditions, and within this plane the Fourier expansion of the potential for the (x,y) coordinates are constructed. To performed this calculation we considered a conventional unit cell, i.e. a cubic with bulk Fe lattice parameter. We built XY planes of grid points r_|| along the z coordinate with no regular spacing (more dense around atomic layer positions) for discretization. We proceed similarly for the 9Fe/3MgO/8Fe(001) super-cell.

To obtain the Fourier components of the potential within this XY unit plane, we used a two-dimensional plane wave (r_||) defined in the (x,y) coordinates as

where n_|| is a pair of indexes (n₁,n₂) that define the reciprocal lattice vector G_|| = n₁b₁ + n₂b₂, (b₁,b₂) are primitive vectors from a fixed origin of the crystal in the reciprocal space, k_|| represent a point (k_x,k_y) inside the first Brillouin zone in the two dimensional reciprocal space and A is the area of the squared XY unit cell in the real space. The unit cell has a lattice parameter a equal to the experimental Fe-bcc bulk lattice parameter. Two primitive orthogonal vectors t₁ = ai and t₂ = aj, that reproduce a two dimensional crystal, are defined. With these vectors, primitive vectors in the reciprocal space can be constructed, named b₁ = (2π/a)i and b₂ = (2π/a)j. This information together with r_|| = xi + yj and k_|| = k_xi + k_yj define the (x,y) plane wave for our system, Eq. 1.

With the above definitions, the Fourier components of the potential can be obtained by

Note that (z) in Eq. 2 is k_|| independent since it involves multiplication of complex conjugates with the same k_||. In Fig. 1 are displayed the Fourier components of the potential as a function of the z coordinates, considering a few pairs of indexes {m_||,n_||}, for bulk iron and 9Fe/3MgO/8Fe(001) hetero-structure respectively.

III. THEORY OF 3D TUNNELING

In order to calculate tunneling conductance through the hetero-junction, we must solve the 3D Schrodinger equation that in Hartree atomic units looks

where r is the coordinate of the particle, σ indicates spin and V^σ(r) is the potential for the system. If the system has periodicity in the (x,y) coordinates, as in our case, it is possible to reduce the three dimensional Schrodinger equation of Eq. 3 to a 1D one. To obtain the one dimensional Schrodinger equation along the z direction (through the barrier layer) we used an substitution for the wave function Ψ^σ of the whole system of the form

where (r_||) is the two dimensional plane wave defined in Eq. 1 and (z) is a z coordinate dependent function. We substitute Eq. 4 into Eq. 3 and integrate over the (x,y) coordinates. This integration was accomplished after multiplying Eq. 3 by and recalling the orthogonal properties between functions and . This procedure lead us to

where (z) = E - (z) - [k_||+G_||]² and (z) being the Fourier components of the potential defined in Eq. 2. The Eq. 5 form a set of one dimensional coupled second order differential equations that relates the functions {}. In order to solve the set of linear differential equations of Eq. 5 it is necessary to obtain the set of Fourier components of the potential (z). Since the number of Fourier components determine the number of coupled differential equations in Eq. 5, we will have for N Fourier components N coupled differential equations involving (n_|| = n₁ to n_N) functions in each differential equation. Note that we have used here n₁,...,n_N to specify different pair of indexes; do not be confused with the previous notation of n₁ being one component of the pair n_||.

To proceed further we introduce 2N initial conditions e_i at z = 0 in Eq. 5. With this set linear independent solutions {} are found, and the wave functions can be expanded as (z) = (z) using a set of coefficients {α_j}. Finally the wave function of Eq. 4 can be written as

The wave function of Eq. 6 represents the general mathematical solution to the Schrodinger equation of Eq. 3. This solution depends on a set of unknown parameters {α_j} and typically growth exponentially at z → ±∞. To obtain physically acceptable solutions one has to consider additional boundary conditions.

IV.BAND STRUCTURE AND BLOCH FUNCTIONS FOR BULK MATERIALS

In this section we exercise the set system of Eq. 5 to calculate the band structure of bulk Fe and obtain the Bloch functions that propagates through the z direction in the crystal.

We can used the wave function found in the previous section to write the general solution for bulk Fe. It has the form of Eq. 6 with (z) →(z), in which the functions {} are the solutions of the set of coupled differential equations of Eq. 5 using specific Fourier components (z) of the potential for bulk Fe. To find the available Bloch states along z direction we applied Bloch condition, Ψ(r + R) = exp^{ik R}Ψ(r) with R = (R_x,R_y,R_z) a Bravais lattice vector, and its first derivative over z to our Fe wave function. We obtained

where M_r is a 2Nx2N matrix given by

with f_i,j(r) = (r_||)(z). Recalling that the functions (r_||) satisfies

we can introduce Eq. 9 into the M_{r + R} matrix of Eq. 7 and cancel the functions (r_||) at both sides. This procedure reduced the expression to

where

_z is a 2Nx2N matrix similar to the M_r matrix with elements f_i,j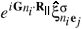(z) = (z).

Since we are interested in bulk Fe, we considered a Bravais bcc vector of the form R = a/2(- + +). With this choice and evaluating the Bloch condition, Eq. 7, at the point r = (0,0,0) we can write the M_{z = 0} matrix as the identity matrix and the interval z ∈ (0,a/2) will not contain singularities. The non-trivial solutions of Eq. 10 can be divided into two classes. The first class consider solutions with positive real or positive imaginary wave vectors; the corresponding eigen-values are denoted λ₊. The second class consider solutions with negative real or negative imaginary wave vectors; the eigen-values are denoted by λ_-. The Bloch states found with λ₊ and λ_- are associated to each branch of the band diagram. The eigen-values of the propagating waves have |λ_±| = 1 and for evanescent waves |λ_±| 1. The evanescent states come in pairs, since it is easy to show that for every solution λ₊ there is a corresponding solution λ_- = 1/λ₊. It can be shown that the propagating states also come in pairs, i.e., for every propagating wave λ₊ there is a λ_- propagating wave [19]. In total we will find k_zi (i = 1,2N) wave vectors (real or imaginary) each one associated to an eigen-vector (α₁,α₂,...,α_2N) → (_i1,_i2,...,_i2N). This implies that we can built 2N solutions for the bulk Fe. Each one of these solutions (that can represent traveling or evanescent waves) can be written as

Typically for any given energy there are few propagating states. For bulk Iron this number is never more than three. It may be also an energy interval where no propagating states exists, that corresponds to the gap in the electron spectrum. The wave functions as given in Eq. 11 are suitable for calculating the transmission through the barrier in the hetero-structure. This is the goal of the next section.

V. CONDUCTANCE

In order to solve the tunneling problem we divided and distinguished three different regions in our system. Two semi-infinite bulk Fe systems, to the right (Region I) and to the left (Region III) of the barrier, where potential is assumed to be perfectly periodic and one central barrier (Region II). The central barrier (of length b) is formed by the 9Fe/3MgO/8Fe(001) MTJ. This is done in order to simulate a continuous transition of Bloch states from the semi-infinite Fe bulk system to the central barrier at both sides of the barrier. We proceed as follows.

First we must built the general solutions for Regions I, II and III. These are

where can be evanescence or traveling wave functions and ({A_i,I},{A_i,III}) his respective amplitudes. The solution in the central barrier can be written as

where the wave functions have the general form of Eq. 6. In order to write the wave function , we need to find the solutions of the set of coupled equations of Eq. 5 in Region II; we called these solutions . The function have no Bloch properties, it is only a bridge between Regions I and III.

To relate the amplitudes of the wave functions between Regions I and III ({A_i,I},{A_i,III}), we imposed to the solutions Φ_I, Φ_II and Φ_III the continuity of the wave function, and its first derivative, at the matching point between Regions I and II (r = r₁), and between Regions II and III (r = r₂). For convinience we choose r₁ = (x,y,-b/2) and r₂ = (x,y,b/2).

After some matrix operations we can related the wave function amplitudes of Regions I and III as

where T = is called the transfer matrix. Here Q_b/2 and Q_-b/2 are identical matrices with elements given by Q_ij = _ji, with {i,j} = 1...2N, and P_z is a matrix defined as in Eq. 8 with elements f_i,j(r) = (z).

To obtain S from T we procedure as follows. We first switch from T to a matrix by means of a linear transformation. The scattering matrix relates the outgoing amplitudes of the wave functions of Regions I and III with their incoming ones. To proceed further we must define a priori the positive and negative directions of propagation of the traveling and evanescent modes. This requirement is necessary since in order to build up the scattering matrix we must distinguished between our solutions the incoming and outgoing waves. We define as the positive direction of propagation of a Bloch function (from left to right) to the mode that have a positive real wave vector and positive group velocity v_g. We considered as the negative direction of propagation (from right to left) the case when we have positive real wave function and negative group velocity. Since the solutions of Eq. 11 come in pairs, we determined the direction of propagation of the pair by defining the direction of propagation of one member of the pair. For the evanescent states the positive direction (from left to right) is define as the direction in which the wave function decays and the negative direction (from right to left) as the direction in which it grows. In this sense the positive direction of propagation in Regions I and III are related to the incoming and outgoing waves respectively. On the other hand the negative direction of propagation in Regions I and III are related to the outgoing and incoming waves respectively.

In order to calculate the total conductance of the system we need to select from the matrix the transmission elements that refers to propagating modes (this modes fulfill |λ_±| = 1) and discard the ones that refers to evanescent modes (|λ_±| 1). This is necessary since after the tunneling and away from the central barrier the evanescent solutions can not define a current flow. So all transmission elements that relates amplitudes that are associated to |λ_±| 1 modes must be removed from the scattering matrix. This is performed by eliminating such rows and columns from the scattering matrix. After this procedure, the transmission elements _ij that survived need to be normalized by the factor . Here v_gi and v_gj are the group velocities, i.e. v_g = ∇_kε(k)/ħ, in the z-direction of the Bloch functions i and j involved in the calculation of _ij. Introducing the velocities results from flux normalizing the modes, which is required by current conservation. The coefficients t_ij = ij found in this way defines the transmission elements of the scattering matrix S.

After eliminating all evanescent contributions and normalizing the remaining and coefficients by their group velocities we arrived at the scattering S matrix

were only transmission through Bloch states were considered.

The tunneling conductance through the barrier in the hetero-structure can be easily calculated by use of a very general result due to Fisher and Lee [15]. The Fisher and Lee formula relates the conductance of the system to the probability of a Bloch electron in one of the Fe electrodes (with chemical potential µ₁) being transmitted through the MgO barrier to the opposite electrode (with chemical potential µ₂). The net current in the Fisher and Lee approach yields the following conductance formula

where the t_ij are the elements of the transmission t matrix that represents the transmission through the barrier of an electron in a channel i using channel j. We show conductance results for the system within a few modes model in the next section.

VI. RESULTS

In this section we applied the developed formalism to a few modes model. For this purpose we focus in the conductance calculation of the Fe/MgO/Fe hetero-junction when five functions (r_||) were considered for the expansion of the set of linear ordinary differential equations of Eq. 5. The five functions we choose have n_|| equal to (0,0) and (±1,±1) to obtain a symmetric solution. Since we will focus only in the conductance through the Γ &– H direction, we set k_x and k_y equal to zero.

The transmission between zero and one Hartree obtained with the above procedure for the two modes model are display in Fig. 2. We have considered in our calculations energies that lies above the higher hetero-structure potential since for lower energies a total reflection is observed. From Fig. 2 we observed a very low transmission between 0.22 and 0.55 Hartree, increasing up to its maximum value of one when it approaches the band gap. The transmission maintained this maximum for a small energy interval and near the band gap it drops approximately one order of magnitude. After the gap we can clearly identify from our results some resonance behavior. The origin of these resonances are the available narrow energy bands inside the barrier that allows the Bloch states to propagate through the hetero-junction. We identify three resonance peaks in this region as shown enclosed in Fig. 2 in linear scale. After the resonance, the transmission drops three order of magnitude and slowly start to increase.

The results presented in Fig. 2 refers to the direct transitions. We found very low (close to zero) inter-channel transmission in the whole range of energy treated. However we obtained interesting inter-channel reflecting results in the two modes regime between 0.218 and 0.386 Hartree. In this interval the direct reflections are much more smaller than the non-direct ones. This suggest a process in which different modes preferred not their own channel to performed the reflection. We did not observe this behavior in the two modes regime between 0.926 and one Hartree in which almost all the reflection is carried out in a direct way.

It is also important to comment that the transmission experience a three order of magnitude jump when we changed from two to one mode regime at the energy value of 0.387 Hartree. Probably the system experiences some pressure change caused by the appearance of the non-propagating evanescent modes. This change in pressure slightly shrink the system helping in this way the propagation of the Bloch state.

VII. CONCLUSION

In this work we studied multi-channel tunneling through an Fe/MgO/Fe(001) hetero-junction barrier. However, the developed multi-channel formalism is valid for any metal/dielectric/metal hetero-junction. The basic idea of our (k_||,z) formalism is the way to transform and solve the 3D Schrodinger equation, which describes Bloch states being reflected from and transmitted through the barrier, into a set of ordinary second order differential equations. This set of equations describes both traveling and evanescent solutions of the Schrodinger equation for the metal. Within the sub-space of the traveling Bloch states we obtained a scattering matrix that transfer incoming states to outgoing ones. We extract from this scattering matrix the transmission and reflection coefficients necessary for the implementation of Fisher and Lee formula for conductance.

This formalism was applied to a five modes model that generates two non-trivial Bloch states. Although simple, this two modes model pointed out important features like resonant tunneling and surface reflection due to bands mismatch that must be taken into account in order to properly calculate the conductance of more sophisticated problems. If we consider to go further than mean field approximation and/or to take into account electron-electron and electron-phonon interaction then Tunneling Hamiltonian is a very efficient approach.

The accuracy of the mean-field potential that feel individual electron is one of the most important points in any ab initio calculation. We have experience in some cases a considerable 25 per cent difference in the conductance calculation with variations in the hetero-junction potential amplitude not greater than 5 per cent. In this work the electronic and magnetic properties of Fe/MgO/Fe(001) hetero-junction were obtained by performing density-functional calculations with generalized gradient approximation for the exchange-correlation potential.

As a part of our results we have found simple analytical parametrization for the Fourier components of the hetero-structure potential. As a function of the coordinate z they have only weak, cusp like singularity at the ion position. The regular behavior of these parameters easily permits the generation of any amount of Fourier components. Another tight spot that we resolved in the present work is the problem associated to infinite leads. As shown in Sec. II, we carefully match the electronic charge density distribution and potential profile between the hetero-junction and bulk Fe.

The conductance through the Fe/MgO/Fe hetero-junction for the two modes model show that even in this simple case the multi-scattering behavior is present. The calculation of the available coefficients in the scattering matrix S show us exactly what fraction of the incoming Bloch state was reflected/transmitted using the individual available channel. This is very important if we want to identify new mechanism of tunneling in scattering problems or the importance of a particular available channel of transmission in bulk materials.

Two important points were considered in our conductance calculation in order to obtain reliable results, the group velocity of the traveling states and the proper direction of propagation of these states inside the crystal. The normalization of the transmission coefficient by the group velocity is extremely important if we expect flux conservation in our system since different modes can tunnel along channels associated with different group velocities. Furthermore the group velocities need to be precisely calculated.

Finally a few words about the enhancement of the method to finite bias or the calculation of the I &– V curve. For small transmission coefficients our approach can be generalized naturally. First self-consistent potential should be generalized for finite chemical potential difference. Second, evanescent states also bring contribution to the current that might be taken into account throughout generalization of the scattering matrix. This research is under way and will appear shortly. We believe that the theory and results of this work could be used as guidance in more detailed investigations of multi-channel tunneling and calculations of transport in nano-structures.

acknowledgments

The authors acknowledge financial support from "Financiadora de Estudos e Projetos - FINEP" and Brazilian "Ministério da Ciência e Tecnologia - MCT".

(Received 01/07/2008)

• [1] W. Wulfhekel, M. Klaua, D. Ullmann, F. Zavaliche, J. Kirschner, R. Urban, T. Monchesky and B. Heinrich, Appl. Phys. Lett. 78, 509 (2001).
• [2] M. Bowen, V. Cros, F. Petroff, A. Fert, C. M. Boubeta, J. L. Costa-Krämer, J. V. Anguita, A. Cebollada, F. Briones, J. M. de Teresa, L. Morellón, M. R. Ibarra, F. Güell, F. Peiró and A. Cornet, Appl. Phys. Lett. 79, 1655 (2001).
• [3] C. Tusche, H. L. Meyerheim, N. Jedrecy, G. Renaud, A. Ernst, J. Henk, P. Bruno and J. Kirschner, Phys. Rev. Lett. 95, 176101 (2005).
• [4] S. G. Wang, G. Han, G. H. Yu, Y. Jiang, C. Wang, A. Kohn and R. C. C. Ward, J. Magn. Magn. Mater. 310(2), 1935 (2007).
• [5] R. Matsumoto, A. Fukushima, T. Nagahama, Y. Suzuki, K. Ando and S. Yuasa, Appl. Phys. Lett. 90, 252506 (2007).
• [6] T. Marukame, K. Matsuda, T. Uemura and M. Yamamoto, Jpn. J. Appl. Phys. 44, 6012 (2005).
• [7] Stuart S. P. Parkin, C. Kaiser, A. Panchula, P. M. Rice, B. Hughes, M. Samant and S. -H. Yang, Nat. Mater. 3(12), 862 (2004).
• [8] S. Yuasa, T. Nagahama, A. Fukushima, Y. Suzuki and K. Ando, Nat. Mater. 3(12), 868 (2004).
• [9] S. Yuasa, A. Fukushima, H. Kubota, Y. Suzuki and K. Ando, Appl. Phys. Lett. 89, 042505 (2006).
• [10] S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. von Molnár, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Science 294, 1488 (2001).
• [11] X. Liu, D. Mazumdar, W. Shen, B. D. Schrag and G. Xiao, Appl. Phys. Lett. 89, 023504 (2006).
• [12] D. A. Allwood, G. Xiong, C. C. Faulkner, D. Atkinson, D. Petit and R. P. Cowburn, Science 309, 1688 (2005).
• [13] P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, and J. Luitz, WIEN2k, an Augmented Plane Wave and Local Orbitals Program for Calculating Crystal Properties, edited by K. Schwarz, Techn. Univ. Wien, Austria (2001).
• [14] P. A. Khomyakov and G. Brocks, Phys. Rev. B 70, 195402 (2004).
• [15] D. S. Fisher and P. A. Lee, Phys. Rev. B 23, 6851 (1981).
• [16] A. Bagrets, N. Papanikolaou, and I. Mertig, Phys. Rev. B 75, 235448 (2007).
• [17] P. Hohenberg and W. Kohn, Phys. Rev. 136, B864 (1964).
• [18] W. Kohn and L. J. Sham, Phys. Rev. 140, A1133 (1965).
• [19] L. Molinari, J. Phys. A Math. Gen. 30, 983 (1997).

Publication Dates

• Publication in this collection
  03 July 2009
• Date of issue
  Apr 2009

History

• Accepted
  01 July 2008
• Received
  01 July 2008