Ground state energy of charged particles clusters by quantum Monte Carlo method

Ground state energy of charged particles clusters by quantum Monte Carlo method

N. L. Moreira^I; J. N. Teixeira Rabelo^II; L. Cândido^II

^IDepartamento de Física, Universidade Federal de São Carlos, C.P. 676, 13.565-905, São Carlos, SP, Brazil

^IIInstituto de Física, Universidade Federal de Goiás Campus Samambaia, 74001-970 Goiânia, GO, Brazil

ABSTRACT

Using variational and diffusion Monte Carlo methods, we have calculated the ground state energy of spinless charged particles (for N < 10) interacting through a repulsive Coulomb potential, moving in two-dimensions and kept together by an external parabolic potential. Using a very simple trial wave function, we obtain results comparable to those of a sophisticated model of a quantum dot.

Keywords: Quantum Monte Carlo; Quantum dot; Ground state

I. INTRODUCTION AND MODEL

With technological advances in the preparation and in the fabrication of microstructures it is now possible to confine electrons and atoms in restricted regions. The principal exemples of experimental progress in this area are semiconductor quantum dots [1] and laser trapping of cold atoms [2]. Semiconductor quantum dots constitute a quasi ideal system for the study of the physical properties of a two-dimensional system of strongly interacting electrons, laterally confined by an external potential. From the theoretical point of view, computer simulation [3, 4] has achieved the greatest success inusmuch as approximate analytical methods [5] have encountered dificulties, since both the many body effects and the individual behavior of each electron have a crucial role in these systems. The major difficulty in the theoretical methods is due to the fact that the electrons in the quantum dots are confined in a very small area and hence they cannot be treated as part of a continuous distribution of charges. These systems, consisiting of a finite number of electrons confined to a small region in semiconductor structures are known as quantum dots and more recently as artificial atoms.

In this paper we report an application of Variational Monte Carlo and Diffusion Monte Carlo method (VMC-DMC) to calculate the ground state energy of a two-dimensional system used as a model for quantum dots. The simulations are performed with a confinement frequency 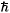w = 0.28 Hartree (H). We consider a system consisting of a small number of spinless charged particles interacting through a repulsive Coulomb potential, moving in two dimensions and an external parabolic potential well. The Hamiltonian is given by

Here,

_i is the position of the ith particle relative to the center of the confinement; m* is the effective mass and e is the dielectric constant of the semiconductor. In effective atomic units, defined by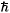 = = 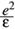m* = 1, the energy and length units are Ry* = m*e²/2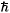²( 4pee₀)² and 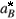= 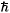²( 4pee₀)/m*e² [6]. The average density n₀ of electrons in the dot may be represented by a parameter r_s defined by n₀ = N/pr² = 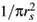. Thus, because the external parabolic confinement is responsible for the average density of electrons, the confinement frequency is w² = e²/4pe e₀m*.

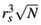II. NUMERICAL SIMULATION

In this work most of the VMC-DMC calculations were performed for clusters with the electron number varying between N = 1 and 10. The simulations were performed in two steps: first we perform a calculation using the VMC method. In this method the main idea is to assume a trial wave function Y_T, which can be optimized with respect to a set of variational parameters a, in order to minimize the expectation value of the energy. In this step use variance minimization of the local energy to improve the trial wave function [7]. Next, we improve the variational estimate by using the DMC method. In this method one propagates the trial wave function in imaginary time t using the operator e^-tH in the long time limit to eliminate higher excited states and project out the ground state. For more details of the VMC and DMC method see ref.[8]. We use a simplified algorithm as suggested in Ref.[8]. In our work we use a simple trial wave function given by a single particle Gaussian times a correlation Jastrow factor product

Here a, b and g are variational parameters. The parameter b is fixed to give the necessary cusp condition when electrons approach one another, r_ij® 0. Parameters a and g are optimized in order to minimize the expectation value of energy and its variance. Several independent Monte Carlo runs consisting of different initial electron distributions are performed in order to make sure that the ground state energy is reached. Physical quantities are obtained for each set of parameters during several independent Monte Carlo runs consisting of approximately 100 000 steps carried out after the system has reached equilibrium.

III. RESULTS AND DISCUSSION

Table I shows the results of DMC for a system of charged spinless particles (column 3) and the results by Pederiva et al. [9] (column 2) for a circular quantum dot in a semiconductor structure using the Quantum Monte Carlo method. We originally intended to compare our results (column 3) to those of Bedanov et al. [3], for a system of classical particles confined by a parabolic potential, in order to get a first estimate of quantum effects for such system. The direct comparison to those results is however puzzling due to the differences in the definition of the system of units, a problem that has been noted by several authors. For this reason we decided to make a comparison with the results of Pederiva [9] for a semiconductor quantum dot. We do not expect excelent agreement since we consider a system of spinless particles. In spite of the differences mentioned above, our results show an overall qualitative agreement and a reasonable quantitative behavior as is shown in Table I. The quantitative differences in the results come basically from the contribution of the exchange interaction to the total energy. The qualitative behavior is brought about by the Coulombic interaction and the parabolic type of confinement. We can see that the values by Pederiva et al. are always above ours. This is expected, since the inclusion of spins will allow for smaller typical distances between electrons, thus augmenting the potential energy and consequently the total energy.

In Fig. 1 we plot the change in the electrochemical potential E_N as a function of N. This change is due to the addition of an extra electron E_N = µ(N+1)-µ(N), where N is the number of electrons in the cluster, µ(N) = E(N)-E(N-1) is the electrochemical potential of the system. As one can see, the electrochemical potential decreases as a function of the number of electrons, and seems to show valleys and peaks in electron numbers 2,6 and 9 that are related to changes in the structure of the cluster in agreement with experiment [10]. The most remarkable change observable in the Figure occurs when the number of particles is equal to six. For this particular number of particles one electron lies in an internal shell and the other five in the external shell. For the configurations with five or less electrons the changes are not so drastic since all the electrons form a single shell.

IV. CONCLUSION

A combination of the variational and diffusion Monte Carlo methods using a very simple wave function provides a good description of a system of spinless charged particles. In spite of this simplicity, our results are in good agreement with more sophisticated models of quantum dots. Because of this, we believe our results could be of interest as a first estimate of quantum corrections to classical approaches.

Acknowledgments

This research was partially sponsored by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) and Fundação Nacional de Apoio a Pesquisa (FUNAPE-UFG). N.L.M is supported by Fundação Coordenacão de Aperfeiçoamento de Pessoal de Nível Superior (CAPES).

Received on 7 November, 2005

• [1] Nanostructure Physics and Fabrication (edited by M. A. Reed and W. P. Kirk) (Academic Press, Boston, 1989).
• [2] New Trends in Atomic Physics, Les Houches, Session 38, (edited by G. Grynberg and R. Stora) (North-Holland, Amsterdam, 1984), Vol. 1, p. 383.
• [3] V. M. Bedanov, and F. M. Peeters, Phys. Rev. B 49, 2667 (1994).
• [4] L. Cândido, J. P. Rino, N. Studart, and F. M. Peeters, J. Phys. Condens. Matter. 10, 11627 (1998).
• [5] P. F. Farinas, G. E. Marques, and N. Studart, J. Appl. Phys. 79, 8475 (1996).
• [6] M. Koskinen, M. Manninen, and S. M. Reimann. Phys. Rev. Let. 79, 1389, (1997).
• [7] C. J. Umrigar, M. P. Nightingale, and K. J. Runge. J. Chem. Phys. 99(4), 2865, (1993).
• [8] B. L. Hammond, W. A. Lester, Jr., and P. J. Reynolds. Monte Carlo Methods in Ab Initio Quantum Chemistry World Scientific lecture and course note in chemistry; vol. 1, ADDRESS, (1994).
• [9] F. Pederiva, C. J. Umrigar, and E. Lipparini, Phys. Rev. B62, 8120 (2000).
• [10] S. Tarucha, D. G. Austing, T. Honda, R. J. van der Hage, and L. P. Kouwenhoven, Phys. Rev. Lett. 77, 3613 (1996).

Publication Dates

• Publication in this collection
  16 Oct 2006
• Date of issue
  Sept 2006

History

• Received
  07 Nov 2005