Fluxes and chern morphisms of hyperbolic orbifolds

Fluxes and chern morphisms of hyperbolic orbifolds

A. A. Bytsenko^I; M. E. X. Guimarães^II

^IDepartamento de Física, Universidade Estadual de Londrina, Caixa Postal 6001, Londrina, PR, Brazil

^IIDepartamento de Matemática, Universidade de Brasília, CEP: 70910-900, Brasília, DF, Brazil

ABSTRACT

Methods of K-theory and spectral theory of Dirac operators are applied to describe the Chern isomorphisms and quantum fields on branes on hyperbolic manifolds.

I. INTRODUCTION

In superstring and superconformal field theories D-branes play a significant role. The K-theory method has been applied to compute D-brane charges [1-3] which identifies with elements of Grothendick K-groups [4-6] for horizon manifolds. The relevant description of the Ramond-Ramond charges in term of equivariant K-theory has been demonstrated in [1, 7-9]. It leads to a formalism of fractional branes pinned on the orbifold singularities which have components in the twisted sectors of the closed strings.

In this note the Chern isomorphism for fluxes and brane charges interpretation is considered. We examine the Chern classes and charges of branes using the methods of K-theory and spectral theory of differential operators related to hyperbolic spaces (for string compactifications with hyperbolic horizons, see for example [10]).

II. RAMOND- RAMOND FIELDS OVER BRANE

The Ramond-Ramond fields and their flux quantization could be formulated in terms of differential K-theory [11, 12]. These fields get precise characterization by means of bundles with connections [13]. The groups K^j(X,U(1)) (see [14] for details) describe the flat Ramond-Ramond fluxes on a compactification X, where j matters modulo two by Bott periodicity and j = 1 for the IIA and j = 0 for the IIB theory. These groups fit the following exact sequence:

The maps from K-theory to cohomology are the usual Chern character maps, that are isomorphisms over the reals. Since the character is one of the features of the K-theory, which is useful in a variety of applications, we shall review briefly the Chern construction in the topological K-theory.

For a finite-dimensional smooth manifold X the Ramond-Ramond phase admits a description of the form [15]:

The component group is given by the torsion classes in Kº(X), while the trivial component consists of the torus H^odd(X, )/(K¹(X)/Tor). The interpretation of the elements of the group K¹(X,U(1)) is complicate, we can restrict ourselves to the case where the cohomology H^odd(X, ) vanishes. The group of fluxes is simply K¹(X,U(1)) @ Tor Kº(X), and the corresponding Ramond-Ramond flux can be represented by a pair (E_c,E_c') of flat vector bundles with rank(E_c) = rank(E_c'), i.e., a virtual flat bundle E_c = E_c-E_c' of rank zero (see Section 3 for notations). In the string theory path integral a torsion Ramond-Ramond flux gives an additional phase factor to a D-brane. A brane can be represented by a K-homology class, that is a map of an odd spin-manifold X (possibly equipped with an additional Chan-Paton vector bundle) into the space-time M [15]. Therefore, the holonomy of the Ramond-Ramond fields over this brane can be associated with the eta invariant of virtual bundle E_c restricted to X. The complex eta functions of hyperbolic spaces will be considered in the next section.

III. CHERN CLASSES AND K-THEORY OF HYPERBOLIC ORBIFOLDS

A.U(n)-gauge bundles and the Chern-Simons invariants

Methods of spectral theory of differential operators can be used in the type II string compactified on spaces with the real hyperbolic horizon X. Let X = G/ be an irreducible rank one symmetric space of non-compact type. Thus G will be a connected non-compact simple split rank one Lie group with finite center, and Ì G will be a maximal compact subgroup. The object of interest is the groups G = SO₁(n,1) (n Î 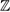₊) and = SO(n). The corresponding symmetric space of non-compact type is the real hyperbolic space X = ⁿ = SO₁(n, 1)/SO(n) of sectional curvature -1. Let X_G = G\G/ be a real compact hyperbolic manifold. The fundamental group of X_G acts by covering transformations on X and gives rise to a discrete, co-compact subgroup G Ì G. Let P = X_G Ä be a principal bundle over X_G with the gauge group = U(n) and let U_XG = W¹(X_G;) be the space of all connections on P; this space is an affine space of one-forms on X_G with values in the Lie algebra of . Suppose that c is any one-dimensional representation of G factors through a representation of H¹(X;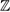). It can be shown that for a unitary representation c: G ® U(n), the corresponding flat vector bundle 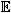_c is topologically trivial (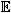_c @ X Ä ⁿ) if and only if : Tor¹® U(1) is the trivial representation. Here Tor¹ is the torsion part of H¹(M;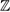) and detc is a one-dimensional representation of G defined by detc(g): = det(c(g)), for g Î G.

A three form flux associates a phase to a Euclidean brane world-volume X_G which is given by the eta invariant of the virtual bundle restricted to X_G. We can express this phase directly in terms of the Chern-Simons invariant. For any extension Ã_c of a flat connection A_c corresponding to c the second Chern character ch₂(_c) ( = -(1/8p²)Tr( Ù )) of _c can be expressed in terms of the first and second Chern classes: ch₂(_c) = (1/2)c₁(_c)²-c₂(_c). The Chern character and the Â-genus, the usual polynomial related to Riemannian curvature W, are given by

Here p₁(W^M) is the first Pontriagin class, W^M is the Riemannian curvature of four-manifold M which has a boundary ¶M = X_G. Thus we have

The integral over the manifold M takes the form

For any representation c one can construct a vector bundle

_c over a certain four-manifold M which is an extension of a flat complex vector bundle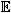 _c over X_G. The second Chern character for the U(1) part is half the Chern-Simons term. The relevant cobordism group vanish, and in fact for three-manifold X_G we found a four-manifold M and extended the U(n) bundle such that manifold M is spin. Therefore the intersection form on M allows one to define the Chern-Simons invariant using 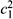. For the chern classes we have c₁(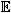_c) Î H²(X_G, 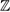), c₂(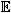_c) Î H⁴(X_G, 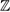), and H⁴(X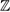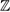_G, ) @ _|G|.

The Dirac index is given by [16-18]

where h(0,_c) is the dimension of the space of harmonic spinors on X_G (h(0,_c) = dimKer _c = multiplicity of the 0-eigenvalue of _c acting on X_G); _c is a Dirac operator on X_G acting on spinors with coefficients in c. The Chern-Simons action CS_U(n)(Ã_c) = -(1/8p²)ò_MTr (Ù ) can be derived from Eq. (5). Indeed,

There exists a Selberg type (Shintani) zeta function Z(s,_c) associated with a twisted Dirac operator _c acting on oriented odd dimensional real hyperbolic spaces. Z(s,_c) is a meromorphic on , and for Â(s²) >> 0 one has [19]:

Thus, finally we get the U(n)-Chern-Simons invariant of an irreducible flat connection on the real hyperbolic three-manifolds:

The value of the Chern-Simons functional on the space of connections at a critical point can be regarded as a topological invariant of a pair (X_G,c). If the one form flux is zero and c₁(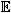_c) = 0 then the flux is measured by c₂(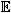_c) Î H³(X_G, U(1)). This group of three-form fluxes is generated by the two-dimensional representation and is given by [15]: H⁴(X_G, 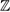) = H³(X_G, U(1)) = 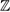_|G|. Using K-theory the groups of fluxes can be computed confirming our computation via the Chern-Simons invariants (for more details see [15]).

B. Brane charges

Before discussing the brane charge formula we begin with some conventions which apply throughout. Let X be an oriented manifold, and let H*(X) be the cohomology ring of X. The Poincaré duality, which is well-known result of differential topology, gives a canonical isomorphism

Let f:Y ® X be a continuous map from Y to X and m = dim Y. For all p > m-n there is a linear map, called the Gysin homomorphism:

f_! : H^j (Y) ® H^j-(m-n)(X)

which is defined such a way that the sequence

is commutative. Thus f_! = , where f_* is the natural push-forward map acting on homology. As an example of that construction let us assume that Y is an oriented vector bundle E over X of fiber dimension . The canonical projection map p:E ® X and the inclusion i :X ® E of the zero section induce maps on homology with p_*i_* = Id. For all j we have the following isomorphisms:

p_! is the Gysin map; it can be associated with integration over the fibers of E ® X. We have p_!i_! = Id, so that p_! = (i_!)^-1. The map i_! is called the Thom isomorphism of the oriented vector bundle E. The particular example j = 0 is an important case of the Thom isomorphism. For j = 0 a map Hº(X) ® (E), and the image of 1 Î Hº(X) determines a cohomology class F[E] = i_!(1) Î (E) , which is called the Thom class of E.

Let us consider U(n) gauge bundle 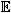on the brane. It has been shown that, as an element of H*(X), the Ramond-Ramond charge associated with a D-brane wrapping a supersymmetric cycle in spacetime f :Y X with Chan-Paton bundle 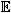® Y is given by

The map

is an isomorphism, and it can be extend to a ring isomorphism [20]: ch: , which maps K^-1(X) onto H^odd(X,). Note that the rational cohomology ring H^even(X, ) has a natural inner product, while the pairing K(X), associated with the cohomology ring K(X), is given by the index of the Dirac operator.

The result (9) is in complete agreement with the fact that D-brane charge is given by f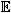_![] Î K(X), and it gives an explicit formula for the brane charges in terms of the Chern character homomorphism on K-theory. The Chern characters ch* (cohomology) and ch_* (homology) preserve the "cap" product Ç. It means that for every it topological space X there is a ₂-degree preserving commutative sequence [21, 22]:

For a finite CW-complex X, K_*(X) is a finitely generated abelian group and ch_* induced an isomorphism K_*(X) ® H_*(X, ) of ₂-graded vector spaces over .

C. Spaces stratified fibered over hyperbolic orbifolds

Here we consider algebraic K-groups which can be applied for computation of charges of branes located at points of spaces stratified fibered over real hyperbolic spaces. Let as before X_G be a closed (means compact and without boundary) connected Riemannian manifold with negative curvature. Let Y¹Ì Y²Ì Y³Ì ... be a sequence of connected compact smooth manifolds and F be a finite group which acting on X_G via isometries and on each via smooth maps. Assume also the smooth embedding is both F-equivariant and -connected. Let Y º Y^¥ = and give Y the direct limit topology. The induced action of F on Y is free. Assuming that is the orbit space X_G× under the diagonal action of F and W º W^¥ is direct . Let X be the orbit space X_G/F and : ® X be the map induced from the canonical projection of X_G×. The each ( = 1,2,..., ¥) is a stratified system of fibrations on X [23] (Definition 8.2).

Let R be a ring with unity and GL_n(R) be the invertible n×n matrices with entries in R. Let E_n(R) be the subgroup of elementary matrices. By definition an elementary matrix E_ij(a) has 1 on the diagonal entry, a Î R-{0} at the (i,j)-position while the remaining entries are 0. Define GL: = lim_n®¥GL_n(R), E(R): = lim_n®¥E_n(R); the limit is taken over the following maps: GL_n(R) ® GL_n+1(R), (a)(a,1). Let

C_* := C₀® C₁® ... ®

be a finite CW-complex.

The Whitehead group Wh(G) of G is C₁([G])/s( < G, -G > ), where C₁([G]) = GL(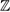[G])/E(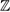[G]), and s: < G, -G > ® K₁(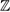[G]) is determine by sending ±g to the 1×1 matrix (±g), "g Î G. As a consequence, Wh(1) = 0. The group Wh(G) has been checked for several classes of groups: for free Abelian groups [24]; for free non-Abelian groups [25]; for the fundamental group of any complete non-positively curved Riemannian manifold [26]; for the fundamental group of finite polyhedra with non-positive curvature [27]; for the fundamental group of any Haken three-manifold [28], etc. The Whitehead group of the finite cyclic group is trivial [29].

Let Y be a contractible; denoting p₁W by G we have result valid all integers n [30]:

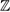Here G_y = p₁(r^-1(y)) for y Î X and (G_y) Ä , (G_y) Ä are the corresponding stratified systems of Abelian groups over X. More precise information contains the following formulas [30]:

where is a stratified system of vector spaces over G\G/, and GÇ

^-1 is a finite subgroup of G.

The isomorphism conjecture of Farrell and Jones [31] states that the algebraic K-theory of the integral group ring 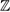G may be computed from the algebraic K- theory of the virtually cyclic subgroups of G (a group G is called virtually cyclic if it has a cyclic subgroup of finite index). For precise statement and definitions see [32]. In [31] the isomorphism conjecture has been proved in lower algebraic K-theory for co-compact discrete subgroups of a virtually connected Lie group, in particular for discrete groups acting discontinuously and co-compactly by isometries on a simply connected Riemannian manifold X with non-positive sectional curvature. In [33] this result has been extended to the discrete groups acting discontinuously on real hyperbolic n-space via isometries whose orbit space has finite volume.

Acknowledgements

The authors would like to thank CNPq and Fundação Araucária (Paraná) for support.

Received on 11 October, 2005

• [1] E. Witten, D-branes and K-theory, JHEP 9812, 019 (1998) [hep-th/9810188].
• [2] S. Gukov, K-Theory, Relality, and Orientifolds, Commun. Math. Phys. 210, 621 (2000) [hep-th/9901042].
• [3] E. Sharpe, D-Branes, Derived Categories, and Grothendieck Groups, Nucl. Phys. B 561, 433 (1999) [hep-th/9902116].
• [4] M. F. Atiyah, K-Theory, Benjamin, New York, 1967.
• [5] M. Karoubi, K-Theory. An Introduction, Springer-Verlag, Berlin 1978.
• [6] D. Husemoller, Fibre Bundles McGraw-Hill, New York 1966.
• [7] D. Diaconescu and J. Gomis, Fractional branes and boundary states in orbifold theories, JHEP 0010, 001 (2000) [hep-th/9906242].
• [8] H. Garcia-Compean, D-branes in orbifold singularities and equivariant K-theory, Nucl. Phys. B 557, 480 (1999) [hep-th/9812226].
• [9] O. Bergman, E. Gimon, and B. Kol, Strings on Orbifold Lines, JHEP 0105, 019 (2001) [hep-th/0102095].
• [10] A. A. Bytsenko, M. E. X. Guimarăes, and J. A. Helayel-Neto, Hyperbolic Space Forms and Orbifold Compactification in M-Theory, Proc. Sci. WC2004, 17 (2004).
• [11] G. Moore and E. Witten, Self-duality, Ramond-Ramond fields, and K-theory, JHEP 0005, 032 (2000) [hep-th/9912279].
• [12] D. S. Freed, Determinant line bundles revisted, Lecture Notes in Pure and Appl. Math. 184 187, Marcel Dekker, New York 1997.
• [13] D. S. Freed, Dirac charge quantization and generalized differential cohomology, hep-th/0011220.
• [14] J. Lott, {$\mathbb R}/{\mathbb Z}$-Index Theory, Comm. in Anal. and Geom. 2, 279 (1994).
• [15] J. de Boer, R. Dijgraaf, K. Hori, A. Keurentjes, J. Morgan, D. R. Morrison, and S. Sethi, Triples, Fluxes, and Strings, Adv. Teor. Math. Phys. 4, 995 (2002) [hep-th/0103170].
• [16] M. F. Atiyah, V. K. Patodi, and I. M. Singer, Spectral Asymmetry and Riemannian Geometry. I, Math. Proc. Camb. Phil. Soc. 77, 43 (1975).
• [17] M. F. Atiyah, V. K. Patodi, and I. M. Singer, Spectral Asymmetry and Riemannian Geometry. II, Math. Proc. Camb. Phil. Soc. 78, 405 (1975).
• [18] M. F. Atiyah, V. K. Patodi, and I. M. Singer, Spectral Asymmetry and Riemannian Geometry. III, Math. Proc. Camb. Phil. Soc. 79, 71 (1976).
• [19] H. Moscovici and R. Stanton, Eta invariants of Dirac operators on locally symmetric manifolds, Invent. Math. 95, 629 (1989).
• [20] M. F. Atiyah and F. Hirzebruch, Analytical Cycles on Complex Manifolds, Topology 1, 25 (1962).
• [21] R. M. Switzer, Algebraic Topology: An Introduction, Springer-Verlag, 1978.
• [22] R. M. G. Reis and R. J. Szabo, Geometric K-Homology of Flat D-Brtanes, hep-th/0507043.
• [23] F. Quinn, Ends of Maps, II, Invet. Math. 68, 353 (1982).
• [24] H. Bass, A. Heller, and R. Swan, The Whitehead group of a polynomial extension, Publ. Inst. Hautes Etudes Sci. 22, 61 (1964).
• [25] J. Stallings, Whitehead torsion of free products, Ann. of Math. 82, 354 (1965).
• [26] F. T. Farrell and L. E. Jones, Topological rigidity for compact nonpositively curved manifolds, Differential Geometry: Riemannian Geometry (Los Angeles, CA 1990), Proc. Sympos. Pure Math. 54, Part 3, American Mathematical Society, Providence, R. I. (1993) 229.
• [27] B. Hu, Whitehead groups of finite polyhedra with non-positive curvature, J. Diff. Geom. 38, 501 (1993).
• [28] F. Waldhausen, Algebraic K-theory of generalized free products, Parts 1 and 2, Ann. of Math. 108, 135 (1978).
• [29] G. Higman, The units of group-rings, Proc. London Math. Soc. 46, 231 (1940).
• [30] F. T. Farrell and L. E. Jones, Algebraic K-theory of spaces stratified fibered over hyperbolic orbifolds, Proc. Natl. Acad. Sci. USA, 83, 5364 (1986).
• [31] F. T. Farrell and L. E. Jones, Isomorphism congectures in algebraic K-theory, J. Amer. Math. Soc. 6, 249 (1993).
• [32] J. F. Davis and W. Lück, Spaces over a category and essembly maps in isomorphim congectures in K- and L-theory, K-theory 15, 201 (1998).
• [33] E. Bercove, F. T. Farrell, D. J. Pineda, and K. Pearson, The Farrell-Jones isomorphism conjecture for finite covolume hyperbolic actions and the algebraic K-theory of Bianchi groups, Trans. Amer. Math. Soc. 352, 5689 (2000).

Publication Dates

• Publication in this collection
  16 Jan 2006
• Date of issue
  Dec 2005

History

• Received
  11 Oct 2005