Abstract
We discuss the gravitomagnetism in the context of scalar-tensor theories of gravity. We obtain the equation of motion of a particle in terms of gravitoelectric and gravitomagnetic fields. We discuss the gravitomagnetic time delay and the Lense-Thirring effect in the context of scalar-tensor theories of gravity. In the particular case of Brans-Dicke Theory, we compare the results obtained with those predicted by general relativity and show that within the accuracy of experiments designed to measure these effects, both theories predict essentially the same results.
On some aspects of gravitomagnetism in scalar-tensor theories of gravity
V. B. BezerraI; A. BarrosII; C. RomeroI
IDepartamento de Física, Universidade Federal da Paraíba, 58059-970, João Pessoa, PB, Brazil
IIDepartamento de Física, Universidade Federal de Roraima, 69310-270 Boa Vista, RR, Brazil
ABSTRACT
We discuss the gravitomagnetism in the context of scalar-tensor theories of gravity. We obtain the equation of motion of a particle in terms of gravitoelectric and gravitomagnetic fields. We discuss the gravitomagnetic time delay and the Lense-Thirring effect in the context of scalar-tensor theories of gravity. In the particular case of Brans-Dicke Theory, we compare the results obtained with those predicted by general relativity and show that within the accuracy of experiments designed to measure these effects, both theories predict essentially the same results.
I. INTRODUCTION
The conjecture that mass currents should generate a field called, by analogy with eletromagnetism, the gravitomagnetic field, goes back to the beginnings of general relativity[1]. Indeed, according to general relativity, moving or rotating matter should produce a contribution to the gravitational field that is the analogue of the magnetic field of a moving charge or magnetic dipole. This field would be expected to manifest itself in a number of effects, such as the Lense-Thirring precession[2], the gravitomagnetic time delay[3], change in the phase of electromagnetic waves[4], among others.
Effects of general relativiy associated with the rotation of massive bodies may be better understood by using a formal analogy with electromagnetism. The idea is that mass currents generate a field called, by analogy with electromagnetism, the gravitomagnetic field[1].
There are indirect evidences of the existence of gravitomagnetism in an astrophysical context and in the weak field and slow motion approximation valid throughout the Solar System[5, 6]. Recently, interest in the subject has been boosted by the concrete possibility that gravitomagnetic effects might be measured with the current technology of laser ranged satellites (LAGEOS and LAGEOS II)[7]. The first accurate measurement of the Lense-Thirring effect, with an error estimate of 10%, was performed using the current technology of laser ranged satellites (LAGEOS and LAGEOS II).[8] It is important to mention the Relativity Gyroscope Experiment (Gravity Probe B)[9], a space mission launched on April 2004 whose aim is to detect gravitomagnetism effects directly. It is expected that these experimental programs will open new possibilities of testing general relativity and other metric theories of gravity [10, 11]. The Gravity Probe B experiment, an ongoing space mission using orbiting gyroscopes, plans to measure the Lense-Thirring effect with an error of about 1%. Certainly, these experimental programs will open new possibilities of testing general relativity against other metric theories of gravity, in particular the scalar-tensor theory.
Scalar-tensor theories of gravity was proposed some years ago by Jordan[12], and Brans and Dicke[13, 14]. Later they were extended in a more general framework[15, 16]. They represent a generalization of the simplest scalar-tensor theory of gravity which is the Brans-Dicke theory[13]. In general scalar-tensor theories of gravity, the gravitational field is not described only by the usual tensor field gmn of general relativity. In addition to this, we have one or several long range scalar fields which also mediate gravitational interaction.
Scalar-tensor theories of gravity has been a subject of renewed interest. Certainly, one motivation for this is the believe that, at least at sufficiently high energy scales, gravity becomes scalar- tensorial in nature[17] and therefore these theories are important in the very early Universe. On the other hand two important theoretical developments have been achieved like, for example, in unification models based on superstrings which naturally associate long range scalar partners to the usual tensor gravity of Einstein[18]. Another motivation for the investigation of scalar-tensor theories is that inflationary cosmology in this framework seems to solve the fine-tuning problem and in this way give us a mechanism of terminating inflationary eras[19]. Apart from the solution of this problem, the scalar-tensor theories by themselves have direct implications for cosmology and for experimental tests of the gravitational interaction[20] and have importance in the early Universe.
Our aim in to obtain the gravitoelectric and gravitomagnetic fields in the context of scalar-tensor theories, write down the equations of motion of a particle in terms of these fields and then compare the results with those predicted by general relativity. In particular, we will compare the results oobtained in the framework of Brans-Dicke theory with the corresponding ones in general relativity. To get this result we will use the fact that, in the weak field approximation, solutions of scalar-tensor theories are simply related to the solutions of general relativity equations for the same matter distribution[21], which is a result extended from the method developed by Barros and Romero[22] to obtain the solutions in Brans-Dicke theory from the corresponding solutions in general relativity, for the same matter distribution, in the framework of the weak field approximation.
This paper is organized as follows. In Section II, we give a brief introduction to the basic ideas of gravitomagnetism in general relativity. Then, in Section III, we show how general relativity and scalar-tensor theories of gravity are related in the weak field approximation. The gravitomagnetic field in scalar-tensor theories is defined in Section IV. We consider the Lense-Thirring effect and the gravitomagnetic time delay in scalar-tensor theories in Sections V and VI, respectively. Section VII is devoted to some remarks.
II. THE GRAVITOMAGNETIC FIELD IN GENERAL RELATIVITY
Let us recall that in the weak field approximation of general relativity we assume that the metric tensor gmn deviates only slightly from the flat spacetime metric tensor. In other words, we assume that gmn = hmn+hmn, where hmn = diag(-1,1,1,1) denotes Minkowski metric tensor and hmn is a small perturbation term. Then, by keeping only first-order terms in hmn and adopting the usual harmonic coordinate gauge  ,µ = 0, the Einstein equations become
,µ = 0, the Einstein equations become
where  and h denotes the trace of
and h denotes the trace of  .
.
We now assume a perfect fluid matter configuration and slow motion. If r denotes the mass density and vi the velocity components, then (1) yields
where terms such as p and vivj/c4 have been neglected. Let us now specialize the equations above to the case of a stationary gravitational field of a slowly rotating body. Then, far from the source we have
from which it follows that
where
0i are the components of the vector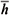 , M and
, M and 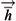 are the total mass and angular momentum of the source, respectively. In close analogy with electrodynamics we define the gravitoelectric field to be
are the total mass and angular momentum of the source, respectively. In close analogy with electrodynamics we define the gravitoelectric field to be 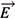 g = -
g = -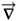 Fg and the gravitomagnetic field to be
Fg and the gravitomagnetic field to be 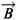 g =
g = 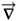 ×
×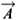 g. It is interesting to see that the condition
g. It is interesting to see that the condition 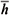 mn,m = 0 leads to
mn,m = 0 leads to 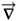 ·
·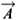 g = 0 (analogous to the Coulomb gauge of electromagnetism).
g = 0 (analogous to the Coulomb gauge of electromagnetism).
Let us note that for the case of a slowly rotating sphere with angular momentum  = (0,0,J), we obtain from (7) in spherical coordinates
= (0,0,J), we obtain from (7) in spherical coordinates
Recalling that the Kerr metric in Boyer-Lindquist coordinates in the weak field and slow motion limit is given by[23]
we see that
0j is the g0j component of (9).It is worth noting that one can easily show by using the geodesic equation
in the slow motion and weak field approximation, that
where the gravitoelectric field is given by
g = -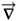 Fg and the gravitomagnetic field can be written as
Fg and the gravitomagnetic field can be written as
With these conditions, the spacetime metric has the form
The Lagrangian for the motion of a test particle of mass m is L = -mcds/dt. To first order in F and 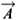 it becomes
it becomes
where g = 1/ . In the weak gravitational field, we assume that the particle has a small velocity. Then, we obtain from (14) that
. In the weak gravitational field, we assume that the particle has a small velocity. Then, we obtain from (14) that
which is analogous to the electromagnetic case. Thus, the equation of motion,  = d
= d /dt, with
/dt, with  = gm
= gm , takes a Lorentz force law form
, takes a Lorentz force law form
From the above result we see that both the gravitoelectric and the gravitomagnetic field are essentially local physical entities. It turns out, however, that nonlocal properties of gravitomagnetism may appear, for example, when we consider the spacetime generated by a spinning cosmic string[24].
III. THE WEAK FIELD APPROXIMATION SCALAR-TENSOR THEORIES OF GRAVITY
Let us consider the action describing the class of scalar-tensor theories[15, 16]. In the so-called Einstein(conformal) frame, the action reads as
where gmn is a pure rank-2 metric tensor, R is the curvature scalar associated to it and G is some "bare" gravitational coupling constant. The second term in the r.h.s. of eq.(17) is the matter action representing a model of a real Higgs scalar field F and V(F) is the symmetry breaking potential. Action (17) can obtained from the original action[15, 16] by a conformal transformation(see, for instance, [25])
where
mn is the physical metric and contains both scalar and tensor degrees of freedom and A2(f) is an arbitrary function of the scalar field.In the Einstein frame, the field equations are written as follows:
where  , which can be interpreted as the (field-dependent) coupling strenght between matter and the scalar field and the energy-momentum tensor is obtained from
, which can be interpreted as the (field-dependent) coupling strenght between matter and the scalar field and the energy-momentum tensor is obtained from
In what follows, we will consider the solution in the weak-field approximation. Therefore, we will expand eqs. (19) to first order in GA2 (f0) in such a way that
where f0 denotes a determined value of the scalar field.
In this approximation,
is the energy-momentum tensor in the framework of scalar-tensor theories, while  is the energy-momentum tensor in general relativity.
is the energy-momentum tensor in general relativity.
In the linearised regime, eqs. (19) can be written as
and
Thus, the linearised Einstein's equation in (23) for a given source is obtained multiplying by the factor A2(f) the solution in general relativity for the same source, with G changed by  . Therefore, in the weak field approximation, the solution in scalar-tensor theories is given by
. Therefore, in the weak field approximation, the solution in scalar-tensor theories is given by
This relation between G and G0 was derived taking into account the corresponding one in Brans-Dicke theory, in which case this relation is valid for a2 =  .
.
IV. GRAVITOMAGNETISM IN SCALAR-TENSOR THEORIES OF GRAVITY
Let us consider the metric of the spacetime in the context of scalar-tensor theories. From (25) and (13), we have
This line element can be written as
where e = A2(f0)[ 1 + 2 a(f0) f(1)].
Now, if we define
the metric will be given by
In close analogy to the general relativity approach, we will have the Lagrangian of a particle of mass m
However, since that
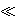 1, the Lagrangian can be simplified to
1, the Lagrangian can be simplified to
Again, we immediately arrive at the equation of motion
where
and
Note that the previous relation can be written as
where which means that the gravitomagnetic in the two theories are related by a factor which depends on the scalar field.
It is interesting to note that the gravitoelectric field is exactly the same of the general relativity case. In the case of Brans-Dicke theory, the scalar field produced by a stationary particle of mass M is given in[13] by e = 2M/c2r(2w+3). Therefore, from (28), it follows that F1 = GM/r. On the other hand, the difference between the two theories, in this approximation, lies in the gravitomagnetic field due to the factor  . Therefore, if we consider that w > 40000 [26], we conclude that there is no difference between the magnitude of the gravitomagnetic field when calculated in the framework of general relativity and Brans-Dicke theory.
. Therefore, if we consider that w > 40000 [26], we conclude that there is no difference between the magnitude of the gravitomagnetic field when calculated in the framework of general relativity and Brans-Dicke theory.
VI. THE GRAVITOMAGNETIC TIME DELAY IN SCALAR-TENSOR THEORIES
As is well known, the Lense-Thirring effect consists in a precession of gyroscopes relative to distant stars, or, equivalently, a dragging of inertial frames, an effect caused by the gravitomagnetic field. Denoting the angular momentum and the angular velocity of the precession by  and
and  , then the torque acting on the gyroscope predicted by general relativity is given by
, then the torque acting on the gyroscope predicted by general relativity is given by
with
Thus in the case of scalar-tensor theories, eq.(38) becomes
To compare the value of W predicted by general relativity with WST, in the particular situation where the Brans-Dicke theory is under consideration, we must ascribe values for w, the scalar field coupling constant. According to the latest experimental results the current value for w greather than 40000. On the other hand, for a polar orbit at about 650 km altitude the axis of a gyroscope is predicted to undergo a precession rate of 42 milliarcsec per year. The expected accuracy of the experiment under these conditions (Gravity Probe B) is about 0.5 milliarcsec per year. Since G0 = ( ) G the predicted value of Brans-Dicke theory is
) G the predicted value of Brans-Dicke theory is
WBD =  W ~ 41.9995 milliarcsec per year.
W ~ 41.9995 milliarcsec per year.
VI. THE GRAVITOMAGNETIC TIME DELAY IN SCALAR-TENSOR THEORIES
The time delay of light is considered a classical test of general relativity and its measurement was first proposed by Shapiro [27]. It can be shown that this effect can be separated into two parts: the Shapiro time delay and the gravitomagnetic time delay, the latter due to the gravitomagnetic field. Assuming again the weak field and slow motion approximation of general relativity one can show that the gravitational time delay D of a light signal travelling between two points P1 and P2 is given by
where kµ = (1, ),
),  denotes the light propagation unit vector and dl = |d
denotes the light propagation unit vector and dl = |d | is the Euclidean length element along the straight line that joins P1 to P2. Now from (4), (7) and (40) it follows that D = Dge+Dgm, where
| is the Euclidean length element along the straight line that joins P1 to P2. Now from (4), (7) and (40) it follows that D = Dge+Dgm, where
is the Shapiro delay and
is the gravitomagnetic time delay.
Clearly, the above equations keep exactly the same form when we go from general relativity to scalar-tensor theories, the only change needed is the substitution Fg®  and
and 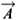 g ®
g ® . Thus we have
. Thus we have
At this point two comments are in order. Firstly, it should be noted that analogously to the general relativity approach the gravitomagnetic echo delay vanishes. Secondly, if the light rays travel along a closed loop around a rotating body (this can be arranged with the help of mirrors), then the time delay due to the gravitomagnetic field depends on the direction the rays go around the loop. Similarly to the general relativity case, the total time diference between two opposite-oriented paths is given by
Note that if we consider Brans-Dicke theory, we get the same results obtained recently[28]. In this case the results obtained in the framework of scalar-tensor theories of gravity is 0.9995 of the corresponding ones in general relativity.
VII. FINAL REMARKS
We have examined the equation of motion of a particle in gravitoelectric and gravitomagnetic fields in scalar-tensor theories of gravity. It has been verified that the gravitomagnetic force predicted by these theories differs of the corresponding force in general relativity by the correction factor  . As a consequence, the Lense-Thirring effect will be qualitatively different in the two theories. From the quantitative point of view the difference is very small as we can see in the Brans-Dicke case[28]. The two effects associated with the so-called gravitomagnetism, namely, the Lense-Thirring effect and the gravitomagnetic time delay in scalar-tensor theories of gravity are quantitatively of the same magnitude as we can see by considering the particular case of Brans-Dicke[28]. Following the same line of reasoning employed in this article it can easily be shown that the equations for the gravitomagnetic time delay in different images due to gravitational lensing in scalar-tensor theories may be obtained again from the corresponding equations in general relativity by using the correction factor
. As a consequence, the Lense-Thirring effect will be qualitatively different in the two theories. From the quantitative point of view the difference is very small as we can see in the Brans-Dicke case[28]. The two effects associated with the so-called gravitomagnetism, namely, the Lense-Thirring effect and the gravitomagnetic time delay in scalar-tensor theories of gravity are quantitatively of the same magnitude as we can see by considering the particular case of Brans-Dicke[28]. Following the same line of reasoning employed in this article it can easily be shown that the equations for the gravitomagnetic time delay in different images due to gravitational lensing in scalar-tensor theories may be obtained again from the corresponding equations in general relativity by using the correction factor  .
.
In which concerns the particular case of scalar-tensor theories of gravity, namely, in Brans-Dicke theory, it is worth calling attention to the fact that Solar System experiments set strict limits in the value of the parameter of this theory, given by w > 40000, which means that a2(f0) < 10-5[26]. Therefore we see that within the precision of the experiment one cannot distinguish one theory from another at least in the context of the Brans-Dicke theory of gravity.
We ackowledge CNPq, CAPES (Programa PROCAD) and CNPq/FAPESQ-Pb(PRONEX) for partial financial support.
References
[1] I. Ciufolini, J. A. Wheeler, Gravitation and Inertia, Princeton University Press, Princeton (1995).
[2] J. Lense, H. Thirring, Phys. Z. 19 (1918) 156 (English translation by B. Mashhoon, F. W. Hehl, D. S. Theisis, Gen. Rel. Grav. 16, 711 (1984).
[3] I. Ciufolini, S. Kopeikin, B. Mashhoon, and F. Ricci, Phys. Lett. A308, 101 (2003).
[4] J. M. Cohen and D. R. Brill, Nuovo Cim. B56, 209 (1968).
[5] L. Stella et al., in Nonlinear Gravitodynamics, edited by R. Ruffini and C. Sigismondi (World Scientific, Singapore, 2003).
[6] K. Nordvedt, in Gyros, Clocks, Interferometers...: Testing Relativistic Gravity in Space, edited by C. Lämmerzahl, C. W. F. Everitt and F. W. Hehl (Springer, Berlin, 2001).
[7] I. Ciufolini, E. Pavlis, F. Chieppa, E. Fernandes-Vieira, and J. Pérez-Mercader, Science, 279, 2100 (1998).
[8] I. Ciufolini and E. C. Pavlis, Nature 431, 958 (2004).
[9] C. W. F. Everitt et al., in Gyros, Clocks, Interferometers...: Testing Relativistic Gravity in Space, edited by C. Lämmerzahl, C. W. F. Everitt, and F. W. Hehl (Springer, Berlin, 2001).
[10] A. Camacho, Gen. Rel. Grav. 34, 1403 (2002).
[11] C. M. Will, Theory and experiment in gravitational physics, Cambridge University Press, Cambridge (1993).
[12] P. Jordan, Nature 164, 637 (1949); Z. Phys. 157, 112 (1959).
[13] C. Brans and R. H. Dicke, Phys. Rev. 124, 925 (1961).
[14] R. H. Dicke, Phys. Rev. 125, 2163 (1962); ibid. 152, 1 (1968).
[15] P. G. Bergmann, Int. J. Theor. Phys. 1, 25 (1968); R. V. Wagoner, Phys. Rev. D 1 , 3209 (1970).
[16] K. Nordtvedt, Ap. J. 161, 1059 (1970).
[17] Thibault Damour and A. Polyakov, Nucl. Phys. B 423, 532 (1994); Gen. Rel. Grav. 26 (1994), 1171.
[18] M. B. Green, J. H. Schwarz, and E. Witten, Superstring Theory, Cambridge University Press, Cambridge (1987).
[19] D. La and P. J. Steinhardt, Phys. Rev. Lett. 62, 376 (1989); P. J. Steinhardt and F. S. Acceta, id. 64, 2740 (1990); J. Garcia Belido and M. Quiros, Phys. Lett. B 243, 45 (1990); J. D. Barrow and K. Maeda, Nuc. Phys. B 341, 294 (1990).
[20] Thibault Damour, Nucl. Phys. B ( Proc. Suppl.) 80, 41 (2000).
[21] M. E. X. Guimarães, L. P. Collato, and F. B. Tourinho, Spacetime and Substance, 2, 71 (2001); R. M. Teixeira Filho and V. B. Bezerra, Phys. Rev. D64, art. 067502 (2001).
[22] A. Barros and C. Romero, Phys. Lett. A245, 31 (1998).
[23] R. H. Boyer, R. W. Lindquist, J. Math. Phys. 8, 265 (1967).
[24] A. Barros, V. B. Bezerra, and C. Romero, Mod. Phys. Lett. A37, 2673 (2003).
[25] Thibault Damour and K. Nordtvedt, Phys. rev. Lett. 70, 2217 (1993); Phys. Rev. D 48, 3436 (1993).
[26] B. Bertotti, L. Iess, and P. Tortora, Nature 425, 374 (2003).
[27] I. I. Shapiro, Phys. Rev. Lett. 13, 789 (1964).
[28] A. Barros and C. Romero, Mod. Phys. Lett. A18, 2117 (2003).
Received on 23 October, 2005
- [1] I. Ciufolini, J. A. Wheeler, Gravitation and Inertia, Princeton University Press, Princeton (1995).
- [2] J. Lense, H. Thirring, Phys. Z. 19 (1918) 156
- (English translation by B. Mashhoon, F. W. Hehl, D. S. Theisis, Gen. Rel. Grav. 16, 711 (1984).
- [3] I. Ciufolini, S. Kopeikin, B. Mashhoon, and F. Ricci, Phys. Lett. A308, 101 (2003).
- [4] J. M. Cohen and D. R. Brill, Nuovo Cim. B56, 209 (1968).
- [5] L. Stella et al, in Nonlinear Gravitodynamics, edited by R. Ruffini and C. Sigismondi (World Scientific, Singapore, 2003).
- [6] K. Nordvedt, in Gyros, Clocks, Interferometers...: Testing Relativistic Gravity in Space, edited by C. Lämmerzahl, C. W. F. Everitt and F. W. Hehl (Springer, Berlin, 2001).
- [7] I. Ciufolini, E. Pavlis, F. Chieppa, E. Fernandes-Vieira, and J. Pérez-Mercader, Science, 279, 2100 (1998).
- [8] I. Ciufolini and E. C. Pavlis, Nature 431, 958 (2004).
- [9] C. W. F. Everitt et al., in Gyros, Clocks, Interferometers...: Testing Relativistic Gravity in Space, edited by C. Lämmerzahl, C. W. F. Everitt, and F. W. Hehl (Springer, Berlin, 2001).
- [10] A. Camacho, Gen. Rel. Grav. 34, 1403 (2002).
- [11] C. M. Will, Theory and experiment in gravitational physics, Cambridge University Press, Cambridge (1993).
- [12] P. Jordan, Nature 164, 637 (1949);
- Z. Phys. 157, 112 (1959).
- [13] C. Brans and R. H. Dicke, Phys. Rev. 124, 925 (1961).
- [14] R. H. Dicke, Phys. Rev. 125, 2163 (1962);
- [15] P. G. Bergmann, Int. J. Theor. Phys. 1, 25 (1968);
- R. V. Wagoner, Phys. Rev. D 1 , 3209 (1970).
- [16] K. Nordtvedt, Ap. J. 161, 1059 (1970).
- [17] Thibault Damour and A. Polyakov, Nucl. Phys. B 423, 532 (1994);
- Gen. Rel. Grav. 26 (1994), 1171.
- [18] M. B. Green, J. H. Schwarz, and E. Witten, Superstring Theory, Cambridge University Press, Cambridge (1987).
- [19] D. La and P. J. Steinhardt, Phys. Rev. Lett. 62, 376 (1989);
- P. J. Steinhardt and F. S. Acceta, id. 64, 2740 (1990); J. Garcia Belido and M. Quiros, Phys. Lett. B 243, 45 (1990);
- J. D. Barrow and K. Maeda, Nuc. Phys. B 341, 294 (1990).
- [20] Thibault Damour, Nucl. Phys. B ( Proc. Suppl.) 80, 41 (2000).
- [21] M. E. X. Guimarăes, L. P. Collato, and F. B. Tourinho, Spacetime and Substance, 2, 71 (2001);
- R. M. Teixeira Filho and V. B. Bezerra, Phys. Rev. D64, art. 067502 (2001).
- [22] A. Barros and C. Romero, Phys. Lett. A245, 31 (1998).
- [23] R. H. Boyer, R. W. Lindquist, J. Math. Phys. 8, 265 (1967).
- [24] A. Barros, V. B. Bezerra, and C. Romero, Mod. Phys. Lett. A37, 2673 (2003).
- [25] Thibault Damour and K. Nordtvedt, Phys. rev. Lett. 70, 2217 (1993);
- Phys. Rev. D 48, 3436 (1993).
- [26] B. Bertotti, L. Iess, and P. Tortora, Nature 425, 374 (2003).
- [27] I. I. Shapiro, Phys. Rev. Lett. 13, 789 (1964).
- [28] A. Barros and C. Romero, Mod. Phys. Lett. A18, 2117 (2003).
Publication Dates
-
Publication in this collection
16 Jan 2006 -
Date of issue
Dec 2005
History
-
Received
23 Oct 2005











































