Anomalous effects of two gap superconductivity in MgB2

Anomalous effects of two gap superconductivity in MgB₂

A. Gurevich

Applied Superconductivity Center, University of Wisconsin, Madison, Wisconsin 53706, USA

ABSTRACT

In this paper a brief overview of anomalous behavior resulting from the two-gap superconductivity in MgB₂ is given. We focus on two characteristic effects: an anomalous enhancement of the upper critical field by nonmagnetic impurities and nonequilibrium interband phase textures which appear as a result of interband breakdown caused by electric field. Both effects distinguish MgB₂ from the existing low-T_c and high-T_c superconductors.

1 Introduction

The discovery of the two-gap superconductivity in MgB₂[1,2,3] (and perhaps in NbSe₂ [4]) has brought to focus new effects of unconventional pairing and multicomponent order parameters y with internal degrees of freedom [5,6]. In particular, MgB₂ has two different s-wave superconducting gaps D_s (0) » 7.2mV and D_p(0) » 2.3mV residing on disconnected sheets of the Fermi surface (FS), which comprises nearly cylindrical 2D parts formed by in-plane s antibonding p_xy orbitals of B, and a more isotropic 3D tubular network formed by out-of-plane p bonding and antibonding p_z orbitals of B. For two weakly coupled s-wave order parameters y₁ = and y₂ = , the internal degree of freedom is the interband phase difference q(r,t) = q₁-q₂. In this case, in addition to the phase-locked states (q = 0, p), peculiar phase textures q(r,t) and collective modes [5] occur.

This paper addresses new electromagnetic effects, which principally result from the two-band superconductivity, making MgB₂ unique among the existing superconductors. Such effects manifest themselves in the following areas: 1. High-field superconductivity in dirty two-gap superconductors due to their anomalous response to nonmagnetic impurities. [7] This makes it possible to greatly increase the upper critical field H_c2 by alloying MgB₂ and optimizing the ratio of intraband scattering rates, as has already been observed. [8] 2. Interband tunneling and intrinsic Josephson effect, which give rise to dislocation-like phase textures in the order parameter, and interband breakdown caused by the electric field. [9] These textures manifest themselves in new effects in nonlinear electromagnetic response.

2 High-field superconductivity

So far all attempts to increase T_cof MgB₂ by doping have been unsuccessful, while the significant potential of MgB₂ for applications is still limited by rather low upper critical fields (0) 3 - 5T and (0) 15 - 19T of MgB₂ single crystals [3,10], where ^ and || correspond to H perpendicular and parallel to the ab plane. As far as H_c2 is concerned, it can be increased by nonmagnetic impurities, following the well-known route for dirty one-gap superconductors in which the zero-temperature H_c2(0) and the slope = dH_c2/dT at T_c are increased proportionally to the normal state residual resistivity r:

where N_F is the density of states at the FS and -e is the electron charge. The same approach has also been applied to MgB₂ in which scattering was introduced by irradiation or atomic substitutions on both B and Mg sites [3]. For instance, in c-axis oriented MgB₂ films [11], r was increased from ~ 1 mWcm to more than 200 mWcm, resulting in » 1T/K and » 1.8T/K, while reducing T_c down to » 31K. Based on these numbers, the extrapolation (1) gives (0) » 20T, still below H_c2(0) » 30T of Nb₃Sn. However, Eq. (1) significantly underestimates the actual H_c2 in two-gap superconductors, thus H_c2 of MgB₂ can exceed H_c2(0) of Nb₃Sn even for » 1T/K which have already been achieved[11,8].

The Fermi surface of MgB₂ provides three different impurity scattering channels: intraband scattering within s and p FS sheets, and interband scattering. Intraband scattering reduces the intrinsic anisotropy of D_s and D_p with no effect of T_c, while the pairbreaking effect of interband scattering is weak due to orthogonality of s and p orbitals[12]. The multiple scattering channels provide the essential flexibility to increase the H_c2 of MgB₂ to a much greater extent than in one-gap superconductors not only by the usual increase of r, but also by optimizing relative weights of s and p scattering rates by selective atomic substitution on B and Mg sites. This follows from recent calculations of H_c2 from the Usadel equations in which all scattering channels in MgB₂ are accounted for via the electron diffusivity tensors for each m-th FS sheet and the interband scattering rates g_mm'. The Usadel equations for two-gap superconductors are: [7]

Eqs. (2) and (3) are supplemented by the self-consistency equations for the order parameters y_m = D_mexp(iq_m),

Here |f_m|²+ = 1, the band index m runs from 1 and 2, N_m is the partial density of states, P = Ñ + 2piA/f₀, A is the vector potential, f₀ is the flux quantum, and w = pT(2n + 1), n = 0,±1, ..., and the matrix elements of the BCS coupling constants l_mm' are given by l_ss » 0.81, l_pp » 0.285, l_sp » 0.119, and l_ps » 0.09 [13] (the indices 1 and 2 correspond to s and p bands, respectively). The Usadel equations were recently used to calculate vortices in MgB₂.[14] The values of g_mm' and can be either calculated from first principles or extracted from the observed H_c2(T) and r(T) curves [7]. For the 2D s band, the principal value along the c-axis is much smaller than the in-plane and , but the anisotropy in 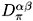for the 3D p-band is much weaker.

Solving Eqs. (2)-(4) [7,14] for g_mm' = 0, yields the following equation for :

where a₁ = 1 + l_- /l₀, a₂ = 1-l_- /l₀, a₀ = 2w/l₀, l₀ = (+4l₁₂l₂₁)^1/2, l_± = l₁₁±l₂₂, w = l₁₁l₂₂-l₁₂l₂₁, h = D₂/D₁, h = H_c2D₁/2f₀T_c, t = T/T_c, and y(x) is the di-gamma function. For equal diffusivities, h = 1, Eq. (5) reduces to the one-gap Maki-deGennes equation ln t + U(h/t) = 0. To account for the dependence of H_c2(q) on the angle between H and the c-axis, D₁ and D₂ in Eq. (5) should be replaced by the angular dependent diffusivities D₁(q) and D₂(q) for both bands [7]:

Eqs. (5) and (6) describe a rather anomalous behavior, depending on the material parameter h = D₁/D₂ which can be varied by disordering either B or Mg sublattices. In the case of large difference between D₁ and D₂, the dependence H_c2(T) can exhibit a significant upward curvature, because the slope at T_c is inversely proportional to the maximum diffusivity, while H_c2(0) is inversely proportional to the minimum diffusivity. Thus, H_c2(0) can be much higher than the one-gap extrapolation (1) suggests. Figs. 1 and 2 show good fit of Eqs. (5) and (6) to pulse high-field measurements of H_c2(T) on resistive 220mWcm c-axis oriented film [8], which has very high H_c2(T) exceeding H_c2 of Nb₃Sn. The fit in Figs. 2 and 3 also revealed that the p band is this film is much dirtier (D_p 0.1 D_s) than the s band, which may be due to distorted and buckled Mg sublattice [16].

Eqs. (5) and (6) also describe an unusual temperature dependence of the anisotropy parameter g(T) = / different from the predictions of the anisotropic one-gap GL theory in which g(T) = const. Because the 2D s band in MgB₂ results in /

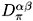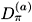/, g(T) can either increase as T decreases if D_p > D_s, or decrease as T decreases if D_p

D_s. The first case is characteristic of cleaner samples [10], whereas the second case was observed on dirty films, as shown in Fig 3. The anisotropy of the lower critical field H_c1(T) is different from that of H_c2(T) [15], as evident from the London penetration depth tensor L_ab in the dirty imit [7]:

For MgB₂, the tensor is a sum of the diffusivities and with markedly different anisotropies and absolute values. Thus, L_ab is always limited by the cleanest band with the maximum diffusivity, so the ratio H_c1(q)/H_c2(q) not only becomes dependent on the field orientation, but its angular dependence turns out to be different at different T.

The two-band superconductivity in MgB₂ provides a new way to boost H_c2, because a higher H_c2(0) is possible for a given slope at T_c. For example, if = 1 T/K and T_c = 40 K, the theory predicts H_c2(0) > 40 Tesla, which exceeds H_c2(0) of Nb₃Sn, even though is still smaller than 2 T/K characteristic of many low-T_c and high-T_c materials. For = 1T/K, the shortest GL in-plane coherence length x(0) = [f₀/2pT_c]^1/2» 3 nm for the s band is still large enough to ensure no significant magnetic granularity and weak link behavior at grain boundaries. Thus, there are no inherent limitations to further increase of toward the high-T_c level of 2 T/K by proper alloying or by quenched-in lattice disorder in MgB₂ with the account of its complex substitutional chemistry. [17] For 2T/K, the field H_c2(0) would approach the paramagnetic limit of 70 Tesla, in which case a more general Eliashberg theory should be used to include strong coupling and spin effects.

3 Intrinsic Josephson effect and interband phase textures

To calculate the interband phase textures q(r,t), we derive the equations of motion for q and the electric field E at T » T_c from the time-dependent Ginzburg-Landau (TDGL) equations, G_m (¶_t - 2pcij/f₀)y_m = -dF/d. Here j is the electric potential, G_m are damping constants, and the free energy F = òd³r(f₁+f₂+f_m+f_int) contains the magnetic part f_m = |Ñ×A|²/8p, the GL intraband part f_m, and the interband energy f_int:

The current density J is a sum of supercurrent and the normal current,

where Q_m = A-f₀Ñq_m/2p, s is the normal conductivity, and the supercurrent is a sum of independent intraband contributions. Static Eqs. (8)-(10) were also derived from the microscopic Usadel equations [7].

For weak interband coupling, g 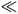a_1,2, the gaps D_1,2 are not affected by the phase textures, in which case the equation of motion for q = q₁-q₂ become [9]

where the relaxation time t_q, the decay length L_q, and the charge coupling parameter a_q are given in Ref. [9]. As follows from Eq. (11), the q-mode does not contribute to the static magnetic response, since divJ_s = 0 for any distribution of bulk supercurrents. However, the q-mode interacts with a nonuniform electric field due to nonequilibrium charge imbalance, divJ_s = -sdivE. This happens near the normal current leads, where the difference in the injected intraband charge densities provides the driving term a_qdivE in Eq. (11) due to the bands asymmetry, G₁g₂¹ G₂g₁. Static distributions q are described by the sine-Gordon equation Ѳq = sign(-g)sin q, which has a single-soliton or staircase solutions similar to the vortex solutions in long Josephson contacts [18]. However, these q-solitons differ from the Josephson vortices, because they do not carry magnetic flux and do not interact with magnetic fields and supercurrents, but can be driven by a nonequilibrium charge density injected from normal electrodes. Thus, equilibrium nonuniform solutions q(x) are always energetically unfavorable as compared to the phase-locked states, q = 0 for g < 0, or p for g > 0, yet dynamic or quenched phase textures can be generated during current-induced interband breakdown.

The equation for E has the form [9]

where J(t) is the driving current density, L_e is the electric field penetration depth, t_e is the charging time constant obtained in Ref. [9], and the coupling term a_eÑ describes an electric field caused by moving phase textures.

Eqs. (11) and (12) which describe nonlinear electrodynamics of a two-gap superconductor at fixed gaps D_1,2 were used to calculate q(x,t) in a current-carrying microbridge of length 2a (Fig. 4). Below the critical current density J_t the bridge is in a phase-locked state, except localized phase kinks at the edges. For J > J_t, the interband breakdown causes periodic generation of q-solitons near the current leads and penetration of phase textures in the bulk, as shown in Figs. 5,6. Here J_t = 2L_q/a_q for L_q

L_e, and J_t = L_e/a_q tanh(a/L_e) for L_q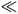 L_e [9].

Eqs. (11) and (12) were solved numerically for the bridge (Fig. 4a) where E(x,t) and q(x,t) are even and odd functions of x, respectively, E(±a,t) = E₀, E'(0,t) = 0, q(0) = 0, q'(±a,t) = 0, and supercurrents in both bands vanish at the normal electrodes, J = sE. In this case q-solitons first appear at the bridge edges, but for J > J_t, they are pushed to the bulk by the strong gradient of E(x). Then the next soliton forms near the edge and the process repeats periodically, resulting in the propagation of two soliton chains from the opposite current leads as shown in Fig. 5. After the first two solitons in the chains collide in the center they stop, while new solitons keep entering the bridge. During this soliton pileup, the mean slope (t) increases, reaching a critical value @ a_q J/ (for J J_t) at which the soliton generation at the edges stops and a static texture forms. During the soliton penetration, t < t_c ~ t_qa/2p, a transient resistance and voltage oscillations are generated. A similar behavior occurs at the point contact (Fig. 4b), in which concentric soliton shells propagate into the bulk, forming a static structure.

A very different kind of soliton dynamics occurs in the 4-terminal geometry (Fig. 4c), for which currents flow in the opposite directions, making 90^° turns around the central stagnation point (x = 0) where Ñq = 0 by symmetry. In this case E(x) is an odd functions of x so the driving charge density divE does not change sign along the horizontal leg of the cross in Fig. 4c, the total charge along the horizontal leg is compensated by the opposite charge distributed along the vertical leg. The asymmetry of E(x) causes generation of solitons and antisolitons at the opposite current leads, which then move toward the center of the cross where they annihilate, as shown in Fig. 6. Such continuous soliton motion takes place if the width w_y of the vertical leg is greater than the width w_x of the horizontal leg, so that the current density in the horizontal leg I/w_x exceeds J_t, while the vertical leg remains in the phase-locked state I/w_y < J_t, where I is the total sheet current. For a L_e, the soliton-antisoliton annihilation in the center is unaffected by the charge imbalance near the current leads.

Two different dynamic states represented in Figs. 5 and 6 have clear analogs in the theory of long Josephson contacts. Namely the transient soliton penetration in the bridge in Fig. 5 is analogous to vortex penetration in a long Josephson junction in a magnetic field H > H_c1, since in both cases the driving terms (charge and magnetization current densities, respectively) are asymmetric functions of x. By contrast, the soliton dynamics in the 4-terminal geometry is analogous to the steady-state annihilation of self-field Josephson vortices and antivortices in a long Josephson junction with a transport current. Because the total charge along the horizontal strip in Fig. 4c is nonzero, all q- solitons are pushed in the same direction (anti-solitons move in the opposite direction), similar to the flux flow of the Josephson vortices driven by the Lorentz force of the transport current.

For J > J_t, the soliton shuttle in Fig. 6 results in continuous voltage oscillations on the bridge. However despite the formal analogy with the behavior of a Josephson junction, the effects considered in this work are due to interband tunneling [5], so the generation of q-solitons does not require any weak links. Unlike the Josephson vortex, a single q-soliton moving with a constant velocity v does not cary magnetic flux, but the continuous phase slippage near the normal lead increases the electric field penetration depth to = (+a_ea_q/st_q)^1/2 for J J_t. [9] This effect increases the excess dc sheet resistance of the strip by R_ex = (-L_e)/sw.

The dynamic phase textures can result in new features of nonlinear electrodynamics of two-gap superconductors. In particular, the soft interband q-mode could manifest itself in rf absorption at frequencies below the small gap D₂. As follows from Eq. (11), interaction of the q-mode with the rf electric fileld E depends on the polarization of E: if E(t) is parallel to the sample surface, then divE = 0, thus the phase mode is not excited by the rf field. However, the q-mode contributes to the rf impedance if the rf field has a component perpendicular to the sample surface.

Other interesting effects could occur in the point contact geometry (Fig. 4c) in which high current densities J ~ J_t near the contact (for example, an STM tip) can be achieved. If the tip is perpendicular to the film surface of a c-axis oriented film, then it mainly injects current into the 3D p band, because the c-axis tunneling into the 2D s band is strongly suppressed. The resulting strong charge imbalance between s and p bands greatly facilitates generation of concentric soliton structures, which can be used to probe the interband breakdown with point contacts. If the currents are simultaneously injected from two point contacts and drained into another current lead, the periodic voltage oscillations between the contacts occur in a way similar to the above-described oscillations in a mictobridge.

This work was supported by the NSF MRSEC (DMR 9214707), AFOSR MURI (F49620-01-1-0464).

References

[1] J. Nagamatsu, N. Nakagawa, T. Muranaka, Y. Zenitani, and J. Akimitsu, Nature, 410, 63 (2001).

[2] A. Liu, I.I. Mazin, and J. Kortus, Phys. Rev. Lett. 87 087005 (2001); H.J. Choi et al., Nature 418, 758 (2002).

[3] P.C. Canfield and G.W. Crabtree, Physics Today, 56, 34 (2003).

[4] T. Yokoya et al., Science 294, 2518 (2001).

[5] A.J. Legget, Prog. Theor. Phys. 36, 901 (1966); Rev. Mod. Phys. 47, 331 (1975).

[6] M. Sigrist and K. Ueda, Rev. Mod. Phys. 63, 239 (1991).

[7] A. Gurevich, Phys. Rev. B. 67, 184515 (2003).

[8] A. Gurevich et al., cond-mat./0305474.

[9] A. Gurevich and V.M. Vinokur, Phys. Rev. Lett. 90, 047004 (2003).

[10] P.C. Canfield, S.L. Bud'ko, and D.K. Finnemore, Physica C 385, 1 (2003).

[11] S. Patnaik et al., Supercond. Sci. Technol., 14, 315 (2001).

[12] I.I. Mazin et al., Phys. Rev. Lett. 89, 107002 (2002).

[13] A.A. Golubov et al., J. Phys. C 14, 1353 (2002).

[14] A.E. Koshelev and A.A. Golubov, Phys. Rev. Lett. 90, 177002 (2003).

[15] V.G. Kogan, Phys. Rev. B. 66, R020509 (2002).

[16] X. Song, et al., Supercond. Sci. Technol. 15, 511 (2002).

[17] R.J. Cava, H.W. Zandbergen, and K. Inumaru. Physica C 385, 8 (2003).

[18] Y. Tanaka, Phys. Rev. Lett. 88, 017002 (2002).

Received on 23 May, 2003

Publication Dates

• Publication in this collection
  25 Nov 2005
• Date of issue
  Dec 2003

History

• Received
  23 May 2003