Construction of exact solutions for the Stern-Gerlach effect

Abstract

We obtain exact solutions for the Schrödinger-Pauli matrix equation for a neutral particle of spin 1/2 in a magnetic eld with a field gradient. The analytical wavefunctions are written on the symmetry plane Y = 0, which contains the incident and splitted beams, in terms of the Airy functions. The time-evolution of the probability densities, |<FONT FACE=Symbol>Y+|</FONT>² and |<FONT FACE=Symbol>Y-|² </FONT>, and the eigenenergies are calculated. These include a small contribution from the field gradient, alpha, proportional to (alpha<img src="http:/img/fbpe/bjp/v31n3/sh.gif">)2/3, which amounts to equal energy displacements on both magnetic levels. The results are generalized for spin S = 3/2, and in this case we found that the m = ±1/2 and m = ±3/2 magnetic sublevels are unequaly splitted by the field gradient, being the difference in energy of the order 0.4 MHz. Replacing real experimental parameters we obtained a spatial splitting of the spin up and spin down states of the order deltaz ~ 4 mm, in accordance to a real Stern-Gerlach experiment.

Construction of exact solutions for the Stern-Gerlach effect

J. Díaz Bulnes and I.S. Oliveira

Centro Brasileiro de Pesquisas Físicas

Rua Dr. Xavier Sigaud 150, Rio de Janeiro - 22290-180, Brazil

Received on 1 February, 2001

We obtain exact solutions for the Schrödinger-Pauli matrix equation for a neutral particle of spin 1/2 in a magnetic eld with a field gradient. The analytical wavefunctions are written on the symmetry plane Y = 0, which contains the incident and splitted beams, in terms of the Airy functions. The time-evolution of the probability densities, |Y₊|² and |Y_-|² , and the eigenenergies are calculated. These include a small contribution from the field gradient, a, proportional to (a)^2/3, which amounts to equal energy displacements on both magnetic levels. The results are generalized for spin S = 3/2, and in this case we found that the m = ±1/2 and m = ±3/2 magnetic sublevels are unequaly splitted by the field gradient, being the difference in energy of the order 0.4 MHz. Replacing real experimental parameters we obtained a spatial splitting of the spin up and spin down states of the order D_z» 4 mm, in accordance to a real Stern-Gerlach experiment.

I Introduction

The experiment of Stern-Gerlach, performed in the first quarter of the 20th century, is introduced in basic quantum mechanics textbooks in order to illustrate the existence of the spin of a particle [1-6]. In spite of its historical importance, and its wide use as an experimental paradigm for the discussion of the concept of measurement in quantum mechanics, authors have failed to exhibit a full, or even particular solution of the problem, that is, the particles analytical wavefunctions and their time evolution, as well as their eigenenergies. A fairly large number of recent works have been published on the subject, as that of Batelaan et al. [7] who proposed an experimental setup where charged particles could be separated by their spins in a "Stern-Gerlach apparatus", contradicting the ideas of Bohr and Pauli at the beginning of the century; Nic Chormaic et al. [8], employing interferometry techniques in a Stern-Gerlach experiment, investigated properties of neutral particles in a beam; Hannout et al. [9] contributed to the theory of measurements in quantum mechanics using the idea of a Stern-Gerlach apparatus. In some other works on the subject [10-13] the role played by the field gradient remains undetermined.

In this paper, we are concerned with a beam of neutral atoms of spin S=1/2 and mass m which penetrates the field region along the x-axis. The magnetic field inside the magnet region can be approximated as :

where

B

₀ represents a homogeneous component of the field, and a(>0) the field gradient along the

z direction. One notices that this field satisfies the equation Ñ ·

B = 0, and also that it can be derived from a potential vector

A = -

y(a

z +

B

₀/2)

i + (

B

₀

x/2)

j.

>From the field given in Eq.(1), one can write the hamiltonian:

and therefore the Schrödinger-Pauli matrix equation:

where

I is the 2×2 identity matrix and s

₁, s

₂ and s

₃ the Pauli matrices. Y = Y(

x,

y,

z,

t) is the two-component spinor:

In what follows we will use the spinor components, Y₊ and Y_-, defined through:

Before proceeding, it is instructive to consider a simple calculation of the expected value for the position of the particle on the z-axis in a instant of time t using (2). This will be given by:

Since the hamiltonian in Eq.(2) is independent of

t, one can write:

and apply the Baker-Hausdorff identity [5]:

In the present case:

>From these expressions one obtains:

Considering the "reduced" hamiltonian,

_r, acting on the wavefunctions on the plane Y = 0:

the problem is greatly simplified for all the terms of order higher than 2 vanish. We will call these functions:

from which one can calculate the expected value of

Z. We obtain the final result:

this result is in accordance with the theorem of Ehrenfest [5]. Thus, if the beam has been previously polarized along the z-axis, by entering the Stern-Gerlach apparatus it will be subject to a force equal to +am_B for spin-down particles ( < _z > (0) = -1/2), and -am_B for spin-up particles ( < _z > (0) = +1/2). Consequently, the beam is splitted by the field gradient, and the particles are separated by their spin direction on the z-axis. In the next section eq.(3) is solved on the plane Y = 0, and the exact wavefunctions are obtained. In section III the stationary wavefunction are determined along with the corresponding eigenenergies. The case S = 3/2 is discussed in Sec.IV and the energy and spatial splittings are calculated in Sec. IV.1 and IV.2, respectively.

II Exact Solutions on Y = 0

On this section we will derive exact solutions for the Stern-Gerlach effect on a symmetry plane. We will consider a magnetic field with field gradient different from zero for x > 0 (direction of the incident particle) and equal to zero for x £ 0. The time-evolution of the particles wavefunctions crossing a Stern-Gerlach apparatus can be obtained analytically on the symmetry plane Y = 0, on which the two equations in (3) become decoupled:

On the basis of the results of the preceeding section, one can expect that the solutions of the above equations will contain a function dependent on the varibles z and t, representing the separation of the beam along the z-axis. Besides, Berry [14] showed that the solutions of the Schrödinger equation of a free-particle can be written as products of AiryAi functions by complex exponential functions whose square modulus evolves without deformation. The fact that Eqs.(10) and (11) contain the coordinate z suggests that the same type of Airy functions can be found here.

We therefore propose as possible solutions of (10) and (11) the following multiparameter functions f₁ and f₂:

and

Where

p

_x is eigenvalue of

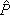
_x, which is in turn conserved. Replacing (13) and (12) in (11) and (10), respectively, one finds that the functions

F and

G satisfy the Airy equation [15] only if the parameters assume the following values:

One notices that with this set of parameters, a and are positive, a necessary condition for | f₁(z, t) | ² and | f₂(z, t) | ² to represent functions which move appart with time. Explicitly, the non-normalized solutions of (10) and (11) are:

One notices that these solutions are correctly reduced to free particle plane waves in the region outside of field, that is,

x £ 0. The time-evolution of the probability density is proportional to the squared modulus of f

₁ and f

₂:

These functions, however, still do not represent physically correct solutions to the problem. First one notes that the AiryAi functions oscillate along the z-axis without decaying for large values of z. To get rid of these oscillations and obtain a proper wavefunction, we simply multiply the solutions (18) and (19) by Heaviside's step functions, Q, which "truncate" the oscillations at the first zero (h_o). Secondly, we introduce a displacement x_o = -1.0188 (first maximum of Ai) in order to make the two functions coincide at t = 0. With this, the final correct time-dependent wavefunctions become:

and

It must be emphesized that the functions (22) and (23) are also solutions of the same set of equations (10) and (11), with the same set of parameters (14), (16) and (17), but w₊ and w_-, which are now given by:

The domains of f₁ and f₂ are ³-{(x, z, t)/z = (h_o/a)-(x_o/a)-bt²} and ³-{(x, z, t)/ z = -(h_o/a)+(x_o/a)+bt²}, respectively. The spin-up and spin-down probability densities become therefore:

and

In order to producer a plot of the functions we define an unit of length, D, as follow:

In terms of D, other physical quantities become:

a remaining arbitrary. Fig. 1 shows | j₁(z, t) | ² and | j₂(z, t) | ² for a = 800. It is apparent that the "spin-up" state separate from the "spin-down" as the particles cross the magnetic field region.

III Eigenenergies

The eigenenergies of the system are given by the solutions of the stationary equation:

where

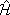
is given by (2). On the plane

Y = 0 one obtains:

Replacing solutions of the type:

one obtains the following equation for the function

R:

where:

and

Defining the new varible h through:

we find the new equation:

wich is the Airy equation. The solution of Eq.(29) is therefore:

Where the step function Q has been introduced, as discussed in the preceeding section. The eigenenergy associated to this functions is:

Similarly, are obtain for f

₂:

with eigenenergy:

We see that the effect of the field gradient is to produce a small positive displacement on the magnetic levels, and consequently, the energy difference

E

₁-

E

₂ does not depend on a.

IV Solutions for S = 3/2

On this section we generalize the results of the preceeding section to the case S=3/2. The hamiltonian for a neutral particle with zero orbital angular momentum and arbitrary spin in a magnetic field B is:

The corresponding Schrödinger-Pauli matrix equation becomes:

where S

_i, with

i = 1, 2, 3, are the spin matrices. For

S = 3/2, over

Y = 0 we have four decoupled equations:

where f

₁, etc., are the components of the four-dimensional spinor.

Following the same proceedure as in the previous section we obtain the following energies:

The main difference in respect to the previous case, is the unequal displacements of the magnetic levels for m = ±1/2 and m = ±3/2. This situation can be exploited to measure the effects of the field gradient on a beam, as shown below.

IV.1 Energy Splitting

In this section we evaluate the magnetic of the contribution of the field gradient to the energy splitting. Let us assume the following values for the physical quantities involved:

With these values we find the following value for the levels E₀ and E₃:

and for

E

₁ e

E

₂:

It is interesting to express the difference in energy between these levels in units of frecuency:

In a real experimental situation we can superimpose to the static fields, a radiofrequency field tuned to frequencies at this range and change the populations of the magnetic levels.

Other orders of magnitudes are:

V Spatial splitting

For the case S = 1/2 one obtain the acceleration by making the argument of the Airy function, eq.(22), constant and derivating in respect to time. From this we have:

Calling l the length of the magnet and L the length between the magnet and the detector, the total deviation of the particle along the z axis is given by:

Replacing the values of the constants given above and making l = L = 0.2m, we find Dz » 4 mm, which is the correct order of magnitude for the splitting observed in a real Stern-Gerlach experiment.

VI Discussions and Conclusions

On this paper we obtained analytical solutions for the problem of a neutral particle with spin S in a static magnetic field with field gradient. These solutions were built from of the Airy functions, which are in turn solutions of the Schrödinger equation in the symmetry plane Y = 0. By choosing adequately the parameters involved, we obtained a discrete energy spectrum, and spin up and spin down wavefunctions which travels apart with time, as in a real Stern-Gerlach experiment. No approximation has been made on the magnitude of the field gradient, a. This contrasts with the usual proceedure (and physically incorrect) of making a << B₀ [6, 16]. Results were obtained for the cases S = 1/2 and S = 3/2. On this last case we showed that the magnetic energy levels are unequally displaced by the field gradient, and that the splitting is on the KHz - MHz frequency range. The calculated spatial splitting is in accordance with what is observed in a real Stern-Gerlac! h experiment.

As a final remark we mention that Eqs (10) and (11) predict another interesting feature, the fact that in a real Stern-Gerlach experiment the separation of spin up and spin down particles is not complete, as stated in [17]. We found further soltions of those equations which show an admixture of spin state waves travelling in oposite direction [18].

Acknowledgments

One of us, JDB, is thankful to Prof. H.G. Valqui (UNI, Lima) for useful sugestions concerning some topics of this work.

• [1] A. Bohm, Quantum Mechanics Foundations and Applications, Springer-Verlag, New York (1993).
• [2] D.I. Blokhintsev, Quantum Mechanics, D. Reidel Publishing Company, Holland (1964)
• [3] P.R. Holland, The Quantum Theory of Motion, Cambridge University Press. Cambridge (1995)
• [4] R.G. Winter, Quantum Physics, Sec. 2.9, 8.1 and 8.2, Wadsworth Publishing Company, California (1979).
• [5] F. Schwabl, Quantum Mechanics, Springer, Berlin (1995).
• [6] J.L. Martin, Basic Quantum Mechanics, Oxford Science Publications, Oxford (1982).
• [7] H. Batelaan, T.J. Gay, and J.J Schwendiman, Phys. Rev. Lett. 79(23), 4517 (1997).
• [8] S. Nic Chormaic, Ch. miniatura, O. Giorceix, B. Viaris de Lesegno, J. Robert, S. Feron, V. Lorent, J. Reinhardt, J. Baudon and K. Rubin, Phys. Rev. Lett. 72(1), 1 (1994).
• [9] M. Hannout, S. Hoyt, A. Kryowonos and A. Widon, Am. J. Phys. 66(5), 377 (1998).
• [10] D.E. Platt, Am. J. Phys. 60(4), 306 (1992).
• [11] M.F Barros, J. Andrade and M.H. Andrade, Ann. Fond. Louis de Broglie 12(2), 285 (1987).
• [12] M.F Barros, J. Andrade and M.H. Andrade, Ann. Fond. Louis de Broglie 13(1), 69 (1988).
• [13] M.I. Shirokov, Ann. Fond. Louis de Broglie 21(4), 391 (1996).
• [14] M.V. Berry, N.L. Balazs, Am. J. Phys. 47(3), 264 (1979).
• [15] N. Bleistein and R. Handelsman, Asymptotic Expansions of Integrals, Dover Publications, New York (1986)
• [16] J.M. Gracia-Bondía, Trevor W. Marshall and Emilio Santos, Phys. Lett. A 183, 19 (1993).
• [17] C.W. Müller and F.W. Metz, J. Phys. A 27, 3511 (1994).
• [18] J. Díaz Bulnes, Construção de Soluções Exatas e Aproximadas para o Efeito Stern-Gerlach, MSc. Thesis, CBPF (2000)

Publication Dates

• Publication in this collection
  27 Mar 2002
• Date of issue
  Sept 2001

History

• Received
  01 Feb 2001