Emergence of log-periodic oscillations in periodic and aperiodic Ising models

Emergence of log-periodic oscillations in periodic and aperiodic Ising models

R. F. S. Andrade

Instituto de Física - Universidade Federal da Bahia

Campus da Federação

40.210-340 - Salvador - Brazil

Received on 15 August, 2000

This work analyzes the emergence of log-periodic oscillations in thermodynamic functions of Ising models on hierarchical lattices. Several situations, where the exchange interactions are periodic or aperiodic, are taken into account. High precision values for the thermodynamic functions are numerically obtained with the method of transfer matrices. Fitting the curves close to the critical temperature leads to the values of the critical exponents and to the period and amplitude of the oscillations. The first two quantities are found to agree with the results predicted by the renormalization group. The amplitude of oscillations, which are minute for both periodic systems and those with aperiodic irrelevant fluctuations, are significantly enhanced for systems with aperiodic relevant fluctuations. Distinct morphologies of the oscillating pattern are discussed, where oscillations are respectively sinusoidal and with a significant contribution of higher order harmonics.

I Introduction

Log-periodic oscillations constitute a general property of systems with discrete scale invariance [1]. They have been reported in many different systems in which there is discrete scale invariance in the lattice on which the model is defined (e.g. geometric fractals [2, 3]), or in the way coupling constants appear over a Euclidean lattice [4], or both [5, 6]. Their presence has been discussed since the early days of the renormalization group (RG) approach to phase transitions in spin models [7], as a multiplicative log-periodic factor in terms of the reduced temperature appears in the general solution of the renormalization transformation. Despite this, only recently has this phenomenon received due attention, in the form of detailed analyses of some models and reviews.

This can be understood by the fact that these oscillations generally have such minute amplitudes that they are hardly detected in the most usual analyses, e.g., in the evaluation of the critical exponents. However, the recent investigation of a large number of deterministic aperiodic models, where fluctuations in the value of the coupling constants alter the system from the original periodic counterpart, has brought this subject to light. The reason can be better discussed in the light of Luck's criterion for relevant or irrelevant fluctuations [8]. According to it, relevant fluctuations are able to promote a structural change in the RG flow diagram of the model, so that the properties at the critical point are no longer described by the fixed point (FP) of the original homogeneous model. On the other hand, irrelevant fluctuations leave unchanged the flow diagram, so that the critical exponents remain the same as in the homogeneous case. The relevant or irrelevant character depends on the spin model, on the lattice used, and on the geometric properties of the aperiodic sequence that is used to define the new values of the coupling constants. The important feature herein is the fact that relevant fluctuations have a general tendency to weaken criticality. So they enhance the magnitude of the log-periodic oscillations of the aperiodic systems which can be identified and conveniently analyzed.

The above observations will be illustrated in this work, which analyzes log- periodic oscillations in periodic and aperiodic Ising models on hierarchical lattices. We proceed with the evaluation of all thermodynamic functions of the models with a transfer matrices (TM) scheme [9], which amounts to iterating a series of maps for such functions at the successive steps of construction of the lattice until numerical convergence is achieved. This work is the third of a series of papers; in the former two [5, 6], we developed the method for the case of hierarchical lattices, investigated the general properties of some models and characterized the oscillations for a situation with aperiodic relevant fluctuations. We concentrate now in the characterization of oscillations for two other cases, one with periodic interactions, the other with aperiodic irrelevant fluctuations. We show that, despite much smaller amplitudes than in the former case, oscillations are present for all thermodynamic functions. Their period can be expressed in terms of the eigenvalues of the critical sets (fixed points or higher period cycles) within the RG analysis. Regarding their morphology, we show that, for the periodic cases, oscillations are almost sinusoidal for both T > T_c and T < T_c. On the other hand, for the irrelevant aperiodic case, oscillations have significant contributions of at least two harmonics for T below and above T_c . In both cases, the morphology of the oscillations is distinct from those in the model with relevant fluctuations.

The rest of the work is organized as follows: In Sec. II we define the hierarchical lattices and aperiodic sequences used to induce fluctuations in the spin-spin exchange couplings; in Sec. III we discuss the key steps of the transfer matrix formalism; in Sec. IV we present the results obtained from fitting the data, where we emphasize the question of single or higher order harmonic contributions in the periodic function; finally, Sec. V closes with concluding remarks.

II Hierarchical lattices and aperiodic sequences

Hierarchical lattices [10, 11, 12] are graphs which are constructed by starting from a single line segment linking two (root) sites and following a substitution rule that amounts, for all subsequent generations, to replacing any single segment by a unit cell composed of a set of line segments and intermediate sites. Their importance for the analysis of phase transitions of magnetic systems is mainly due to two facts: i) they are exactly scale invariant, so that they are suitable for the use of mathematical tools based on this key property, as RG and the adapted TM; ii) despite the fact that they cannot be realized in any finite dimensional Euclidean space, magnetic models defined upon such lattices constitute approximations, within the Migdal-Kadanof renormalization group, to the corresponding models on Euclidean lattices, so that they may lead to results with some relevance for actual physical models. For the present work we concentrate on models where the basic cell is constituted by p parallel branches, each one containing a series of b segments. The fractal graph dimension of such lattice is expressed by

so that, if we take b = p, we will keep d_f = 2 constant.

We define the formal Hamiltonian for our investigation by

where s_i = ±1 indicates Ising spin variables, the double sum (i, j) is performed over pairs of first neighbor sites. The bonds J_ij are either constant or defined with the help of the aperiodic sequences which we will discuss soon. In this case, they assume the same values for any p^G path linking the root sites at the G-th generation of construction of the lattice. Finally the field h is uniform for all sites of the lattice, independent of its local coordination.

Inflation or substitution rules of 2 or more symbols are a convenient way to generate sequences which may be periodic or aperiodic. We consider herein two symbol (A and B) inflation rules which are described by

where the sequence starts with one single A symbol. With exception of the trivial b = 1 case, all other sequences are known to be aperiodic. These sequences are very convenient to generate aperiodic models on the hierarchical lattices just discussed. For this purpose it is important to choose the same value for b in (1) and (3), in such a way that the length of the paths between the root sites of the lattice matches with the length of the sequence for any generation G. So, choosing J_ij to be either J_A or J_B, according to the corresponding symbol in the aperiodic sequence, warrants that an aperiodic model will be generated in the lattice.

The fluctuations in the exchange constants have a relevant (or irrelevant) character, according to Luck's criterion, adapted to hierarchical lattices [13, 14], if the following condition is satisfied:

where n is the correlation length exponent of the uniform model. w is the wandering exponent

where l₁ and l₂ are the eigenvalues of the substitution matrix defined as

It is well known that, for the sequences defined in (2.3), corresponding fluctuations on the hierarchical lattices discussed above will be irrelevant for b = 2 and relevant for b = 3. So, if we restrict ourselves to the situations b = p = 2 and 3 we can conveniently characterize the two different situations, keeping constant the value of the fractal dimension d_f .

III Transfer matrix formulation

The details of the TM method for the evaluation of thermodynamic functions of fractal and hierarchical lattices have been presented in earlier works [5, 6], so that we will discuss here only its main steps. Since the hierarchical lattices are bounded by two root sites in any generation G, the effect of all interactions on the way from one root site to the other can be described by a 2x2 TM T_G, which depends only on the 4 distinct states this pair of spins may assume. In such a formulation, T_G incorporates the contribution of the interaction between all intermediate spins. This can easily be done if we recognize that the matrices of two subsequent generations, T_G and T_G+1 , have the same structure, so that a matricial map expressing T_G+1 = T_G+1(T_G) can be obtained. This implies, in turn, that the matrix elements of T_G+1 can be expressed in terms of those of T_G by nonlinear maps. The derivation of such maps constitutes the essential step for the implementation of the method. It must be pointed out that any model on a given lattice will obey the same matricial map, whereas the map for the matrix elements will assume different forms according to the characteristics of the different models. The nonlinear maps can not be integrated exactly, but it is quite easy to integrate them with a numeric algorithm.

The matrix elements are Boltzmann weights that grow very quickly with G leading to numerical overflows. To sidestep this problem, it is wise to use more convenient variables, that are expressed in terms of the matrix elements. So we define, for any generation G, the free energy per spin f_G and correlation length x_G, in terms of h_G and e_G, the eigenvalues of T_G , as

where N_G counts the number of lattice sites in generation G, and M_G = b^G is the shortest distance between the root sites.

The maps for the new variables, which follow from the original maps for the matrix elements, are written in terms of the same set of variables in the preceding generation. In the iteration process, the initial condition is a temperature dependent state which describes the single interaction between the two root spins in the zero-th order (G = 0) generation. The maps are iterated until the desired precision (usually 10^-16) is obtained. Moreover, we can define a generation dependent entropy and specific heat by the derivatives of the specific free energy with respect to the temperature, i.e., s_G = -¶f_G/¶T and c_G = -T ¶²f_G/¶T² . Thus, the enlarged set of maps includes new components for the derivatives of f_G and x_G, which will depend on f_G and x_G and on the same derivatives in the former generation. The same is valid for the derivatives of f_G with respect to the magnetic field, so that maps for the magnetization and susceptibility can be derived. The solutions of the maps are numerically very stable, as evidenced by the reproduction of known properties and critical exponents of the homogeneous systems. The explicit form of the maps for the two situations explored in this work is given in Ref. [5].

IV Results

The formal solution for the free energy in RG indicates that

where t = |T - T_c| /T_c and L is the largest (thermal) eigenvalue of the RG flow close to the critical FP (or other critical set). The function P is an arbitrary period 1 oscillating function, which includes the possibility P = constant. To uncover and analyze the log-periodic oscillations, we integrate the maps in a very narrow t-neighborhood of the critical temperature T_c , the value of which can be evaluated within the TM approach by following the value of T where x ® ¥. In order to follow oscillations over several orders of magnitude, we choose discrete values of T_n such that t_n/t_n-1 is constant and the values log₁₀(t_n) are equally spaced on the log₁₀(t) axis. From the resulting values we evaluate the numerical derivative of log₁₀(g) with respect to log₁₀(t), where g is any of the thermodynamic functions mentioned above, and graph it as a function of log₁₀(t).

We have analyzed models on the two hierarchical lattices discussed in Section II, with b = p = 2 and 3 . As to the choice of the sequences controlling the exchange constants, we have considered the following distinct situations: i) the homogeneous models for b = p = 2 and 3 ; ii) the period 2 model described by the sequence A ® AB, B ® AB on the lattice with b = p = 2 ; iii) the aperiodic model (with irrelevant fluctuations) induced by the sequence (3) with p = 2 on the lattice with b = p = 2. Note that the case of relevant fluctuations induced by the same sequence with p = 3 has already been treated on Ref . Typical resulting plots are shown in Figures 1-4.

Figure 1.
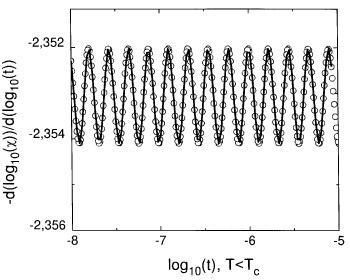
Logarithmic derivative of |c(T) - c(T_c)| with respect to log₁₀(t) vs. log₁₀(t) for the period 2 sequence (A ® AB, B ® AB). The very small vertical scale necessary to show the very small amplitude of oscillations causes makes it necessary to introduce a decay term in . Here and in all other illustrations, open circles indicate the evaluated points and solid line the resulting fit according to the expression 9.

Figure 3. Logarithmic derivative of c with respect to log₁₀(t) vs. log₁₀(t) for the homogeneous model on the lattice with b = p = 2. Note that it has the same period as the curve in Figure 1. Here the amplitude is larger than in the former cases, so that a decay term is not necessary to fit the curve.

To obtain quantitative values for the critical exponents and characterize the morphology of the oscillatory part of the curves, we fit the data with the function

where we have taken N = 2 in almost all fitting procedures. The results are summarized in the Table 1. The parameters c and d in (9) have no precise meaning, but this extra term is necessary to obtain very precise results for some of the functions, expressed by the very low c² values for all fittings. They are related to the distance from the region where the points are evaluated to the very small neighborhood of T_c where the curves are described only by the critical exponent (a) and the amplitudes and phases (b_n and f_n) of the oscillatory function. For some curves we have already reached this neighborhood, so that c º 0.

Figure 4.3
Logarithmic derivative of m with respect to log₁₀(t) vs. log₁₀(t) for the aperiodic model (A ® AB, B ® AA) on the lattice with b = p = 2. Note that the period has doubled in comparison to that in Figures 1 and 3. Here again the amplitude is very small.

IV.1 Periodic cases

The present discussion applies to situations i) and ii). The clear periodic oscillations over 3 decades shown in Figures 1-3 have very small amplitudes (10^-5 or smaller) for the specific heat and correlation length, while only for the magnetic susceptibility do we observe larger amplitudes. As the specific heat curve is characterized by a cusp at T_c, the critical behavior is analyzed for the difference |c(T) - c(T_c)| . For larger values of t , the curve is still far away from the region where it has the form of a constant value superimposed on periodic oscillations. For smaller values of t, round-off errors and the very small differences between neighboring function values induces the presence of large fluctuations in the derivatives, so that the resulting points become meaningless.

The results in Table 1 corroborate the known values for the critical exponents (b = p = 2) as well as those for (b = p = 3) obtained by Haddad [15] and in our previous work [6]. As visually anticipated by the Figures, the computed values for the oscillation amplitude are indeed very small. Comparison of these results with those obtained for relevant aperiodic oscillations indicates that the later are at least two orders of magnitude larger than the corresponding value for the periodic case. The comparison of the contribution of the two Fourier components indicates that the oscillations are indeed very sinusoidal for T below and above T_c, as b₂/b₁ < 10^-2. The evaluation of the period of oscillations indicate that our results are in best accord with those indicated by RG analyses, where L = 1.678 and 2.250 for b = p = 2 and 3 respectively.

The graphs and fittings for the periodic AB case (ii) indicate that it shares the main features of its homogeneous counterpart. This is not surprising as scaling arguments indicate that, after a finite number of steps, related to the intrinsic period of the sequence, the systems evolves asymptotically to the same situation as the homogeneous model. The above evaluation for an explicit situation corroborates the expected results.

IV.2 Aperiodic irrelevant case

This situation is illustrated in Figure 4 for the magnetization, but periodic oscillations are found for all thermodynamic functions. The values for the fitting parameters in Table 1 indicate that the critical exponents remain the same as in the homogeneous case. The magnitude of the oscillations has slightly increased in comparison to the former case. However, the most important difference regards to the period of oscillations. We observe that its value has doubled in comparison to the previous value, i.e., if we write the free energy in the form (8), then P becomes a period 2 function. To bring P back to a period 1 function, the eigenvalue in the denominator of (8) should be squared. In any case the physical meaning is the same: the system only returns to its original configuration after two renormalization steps. Besides that, we also observe that the nearly sinusoidal character of the oscillations has been lost, as now b₂³ b₁ always. This constitutes another important change in the morphology of the oscillations, already observed in the case of relevant fluctuations with T < T_c. However, in the present case, it indicates that some 50% (or more) of the amplitude of the oscillations results from the system trying to follow the original period dictated by the FP eigenvalue. This suggests an interpretation for the observed period doubling: as the FP (and its dynamic properties), which depends only on the lattice and the homogeneous model, is not affected by the aperiodic fluctuations, the critical exponents remain the same, but the period of oscillations is affected by the way the J_A and J_B couplings renormalize back into their own new images. This extra effect seems to be not included in the RG general solution (8). In any case, the contradiction between our results and those predicted by RG needs to be investigated more deeply.

This behavior should be also compared to that observed in the case of relevant fluctuations, where the FP looses its attractive manifold and the period of oscillations becomes related to the eigenvalue of a period 2 cycle in the renormalization flow diagram. In this situation, as in the case of a periodic sequence, our results agree with those of RG. But it should be observed that in this case, the new period 2 cycle directly depends on the fluctuations, which constitutes a crucial difference to the former case.

V Conclusions

In this work we have carefully analyzed the emergence of log-periodic oscillations for periodic and aperiodic (with irrelevant fluctuations) Ising models on hierarchical lattices. Our investigation is based on the TM method, which leads to numerically very precise values for the thermodynamic functions after the iteration of a set of maps. Although these oscillations have been predicted from the solution of the RG maps for systems with discrete scale invariance, they have not been explicited evaluated, except for a few examples where relevant fluctuations are present. Indeed, spin models on hierarchical lattices have been investigated by a large number of authors [12] but, to the best of our knowledge, no explicit evaluations of oscillations, as shown in the previous Section are available in the literature.

Our results show that the magnitude of the oscillations is rather small, which explains the fact that they have been overlooked in the many investigations of the model. The period of oscillation is found to be in accordance with that predicted by RG, for the case of periodic (or homogeneous) systems: it depends only on the eigenvalue of the critical FP. The oscillations are almost sinusoidal for T both below and above T_c, as can be measured by comparing the two Fourier coefficients obtained in the fitting procedure.

The case with aperiodic irrelevant fluctuations presents many differences. Whereas the critical exponents are still controlled by the same FP as the homogeneous case, our investigation shows a slight increase in the magnitude of the oscillations, and a doubling of the period. This result stands in opposition to that offered by RG, according to which the period remains the same and is controlled only by the properties of the homogeneous system. Our result suggests that, in the case of irrelevant sequences, the period depends as well on the modulating sequence. This is supported by the fact that the second Fourier component, which now oscillates with the period of the homogeneous system, has a contribution that is of the same magnitude as the first component. We suggest that the period doubling may be caused by the fact that, whereas the geometrical properties of the lattice and of the homogeneous system favors period 1 oscillations, the renormalization of the J_A and J_B constants back to their original configuration demands a higher number of renormalization steps.

Acknowledgements - The author is much indebted to S.T.R. Pinho for helpfully discussions and suggestions. The work was partially supported by CNPq.

References

[1] D. Sornette, Phys. Rep. 297, 239 (1998).

[2] B. Kutnjak-Urbanc, S. Zapperi, S. Milosevic, and H.E. Stanley, Phys. Rev. E 54, 272 (1996).

[3] J.C. Lessa and R. F. S. Andrade, Phys. Rev. E 61, (2000).

[4] P. E. Berché and B. Berché, J. Phys. A 30, 1347 (1997).

[5] R. F. S. Andrade, Phys. Rev. E 59, 150 (1999).

[6] R. F. S. Andrade, Phys. Rev. E 61, 7196 (2000).

[7] T. Niemeijer and J.M.J. van Leeuwen, in Phase Transitions and Critical Phenomena, Ed. C. Domb and M.S. Green, (Academic, New York, 1976), Vol. 6, p. 425.

[8] J. M. Luck, Europhys. Lett. 24, 359 (1993); J. Stat. Phys. 72, 417 (1993).

[9] R.F.S. Andrade, Physica A 193, 29 (1993).

[10] A. N. Berker and S. Ostlund, J. Phys. C 12, 4961 (1979).

[11] R. B. Griffiths and M. Kaufman, Phys. Rev. B 24, 496 (1981).

[12] C. Tsallis and A. C. N. de Magalhães, Phys. Rep. 268, 305 (1996).

[13] S. T. R. de Pinho, T. A. S. Haddad, and S. R. Salinas, Braz. J. Phys. 27, 567 (1997).

[14] S. T. R. de Pinho, T. A. S. Haddad, and S. R. Salinas, Physica A 257, 515 (1998).

[15] T. A. S. Haddad, MSc. Thesis, Universidade de São Paulo, São Paulo, Brazil, 1999 (in Portuguese).

Publication Dates

• Publication in this collection
  09 Jan 2002
• Date of issue
  Dec 2000

History

• Received
  15 Aug 2000