Unstable periodic structures in nematic liquid crystals

Unstable periodic structures in nematic liquid crystals

M. Simões^1,2, A. J. Palangana¹, and L. R. Evangelista¹

¹ Departamento de Física, Universidade Estadual de Maringá

Avenida Colombo, 5790, 87020-900 Maringá, Paraná, Brazil.

² Departamento de Física,

Universidade Estadual de Londrina

Campus Universitário, 86051-970, Londrina, Paraná, Brazil.

Received 26 October, 1998

We present a review of our recent progress in the description of the elastic and dynamical properties of the unstable periodic (walls) arising in a nematic liquid crystal sample. The Lonberg criterion for the selection of the period of these walls is analyzed. We present a detailed study of the universal character of these walls, which is the basis for a law of corresponding states of these periodic structures. We show the connection of corresponding states with the constant ratio between the Miesowicz viscosity coefficients. Finally, the collapse of these structures is investigated. We show that it is due to the exponential growth of the fluctuations localized along the lines where the director does not bend at all.

PACS numbers: 61.30.Gd, 61.30.Jf, 64.70.Md.

I Introduction

In the last few years, the investigation of the properties of magnetic walls has received a renewed interest from the researchers working in the problem of pattern formation in nematic liquid crystals (NLC). These structures make the transition between adjacent symmetrical distorted regions of the sample and are usually found when, under appropriated conditions, the nematic liquid crystals is submitted to an external field[1].

Consider, for example, a high magnetic field applied to a homogeneously pre-oriented NLC sample in a direction perpendicular to the initial homogeneous direction. A competition between the magnetic susceptibility and the elastic energy takes place. The magnetic field tends to align the director towards its direction and the elastic interaction, due to the cohesion of the NLC with the edges of the sample, tends to retain a uniform orientation of the director. For values of the applied field below a critical value H_c no distortion arises. For those values of the field which are larger than H_c some textures are observed, indicating that the magnetic coupling between the director, , and the filed, , is bigger than the elastic interaction inside the nematic material. When this happens we have the well known Frèedericksz transition that, from the static point of view, has some characteristics of a second order phase transition. That is, for an external field above H_c the director direction changes continuously from the null bending.

Sometimes the director does not comply to the external magnetic field in a homogeneous way. When observed across crossed polarizers the sample exhibits a set of one-dimensional and equidistant lines parallel to the external magnetic field. These lines indicate the existence of walls in the sample. The fundamental element to understand the presence of these lines is the director's p- symmetry. In the nematic medium the director orientation is double valued ( and - are equivalent). Therefore, as it can be observed in Fig. 1, above the Frèedericksz transition the director can bend clockwise or anti-clockwise. This double choice is typical of systems exhibiting a symmetry breaking and, as it is usual in these conditions, two differently orientated portions of the sample can be created. A wall is the continuous bending of the director field connecting these two different configurations. A typical periodic structure is exhibited in Fig. 2.

Figure 1.
Graphical representation of the a LC director's evolution when submitted to an external magnetic field

Figure 2.
Lyotropic nematic calamitic phase in 200 mm thick microslides between crossed polarizers. Magnetic field along the y axis. The figure was obtained from ref. [8].

Despite of its importance for the explanation of this symmetry breaking the p-symmetry cannot explain the astonishing symmetries observed in Fig. 2. The walls are extended as right lines along the direction of the external magnetic field and, furthermore, they are periodically distributed along the direction. They appear in the sample as an one-dimensional and periodic structure. The p-symmetry cannot explain it. There is not an a priori reason leading to this experimental finding. All that the p-symmetry teach us is that there may be regions with different bending of the director. Therefore, some basic information about the building process of the walls is missing.

It was conjectured by Guyon et al.[2] and demonstrated by Lonberg et al.[3] how the elastic properties of the nematic medium are not enough to explain the observed walls geometry. The nematic material is an anisotropic liquid and, at the moment of the walls creation, its internal rearrangement must be taken in account. The director rotation stimulates the motion of the nematic material and it is this internal motion that gives rise to the one-dimensional and periodic outstanding character of the walls[4]. In fact, using the NLC anisotropic properties, it was shown that the observed geometry of the walls results from a coherent internal motion of the nematic material. That is, the external magnetic field creates an unstable situation that must be eliminated as fast as possible. This implies that the motion of the nematic material needs to occur with the smallest possible effective viscosity. In the search for the least effective viscosity the system selects the observed one-dimensional and the periodic geometry. Furthermore, it was shown that these symmetries are connected. That is, one follows from the another one and vice-versa[4].

The periodicity of the walls can be directly measured, and it can be easily observed that their lengths are determined by the external magnetic field and by the elastic constants. Larger is the magnetic field, smaller is the distance between the walls. From the curve of the dependence of this distance on the external magnetic field it was possible to evaluate the ratio between the elastic constants of the nematic material, as well as its magnetic susceptibility [5-9].

With a change of scale, that depends solely on the elastic constants, it was shown that the dependence of the periodicity on the external magnetic field can assume a universal form where all measured data can be put along a sole universal curve. This possibility gives us a powerful insight into the physical nature of these systems because, by a single change of scale, all the particular properties of a given NLC system can be put aside and all that remains is a universal behavior presenting the essential features of some large class[10].

This discovery puts another problem in the nature of these periodic structures. It shows that these walls present a universal behavior that depends only on the elastic constants. But, as we have cited above, the walls cannot be completely explained by an elastic model[11]. If this is so, why are not necessary the dynamical parameters in the scaling that leads the periodicity to a universal behavior? The research in this matter is still in progress. We have demonstrated that the geometry of the walls does not depend on the absolute values of the viscosity, but only on its relative values. On the other hand, as has been pointed out by Kneppe et al.[12], the ratio between the viscosity coefficients seem to exhibit a universal behavior. If this is true, the universality of the walls geometry can be understood in this framework.

The aim of this work is to present a review of the recent progress in the description of the elastic and dynamical properties of these unstable periodic structures in NLC media. An effort is made to present, in a concise and unified way, the successive steps towards a broad understanding of these non-linear aspects of the NLC physics, by focusing several stimulating results we have recently obtained. The reader can find in the bibliography a short but self-contained account of the basic works dedicated to these periodic structures where the fundamental problems of the field are addressed.

The paper is organized as follows. In Sec. the mechanism giving rise to these periodic structures is studied. It is shown that the Frèedericksz transition is indeed a dynamical critical point. The dynamic process by means of which the period of the walls is selected is also explained. In Sec. the quasi-static structure arising as soon as the initial motion of the nematic material stops is studied. It is shown that while the period of the walls is fixed by the motion of the nematic material, the shape of the walls is determined by its elastic, and static, properties. It is also shown that the resulting form for the walls is not stable. These structures decay and the mechanism initiating this collapse is explained[13]. In Sec. our last findings in the physics of the walls are reported. Their behavior when the Frèedericksz threshold is approached is emphasized, and some hypothesis about the planar configuration of these structures are discussed. Some concluding remarks are drawn in Sec. .

II The dynamical arising of the walls

For the Frèedericksz transition study, a sample in the shape of a microslide, whose dimensions (a, b, c) satisfy the relation a >> b >> c, will be considered. Initially the director is uniformly orientated along the direction and, after achieving a homogeneous orientation a fixed, but controllable, magnetic field is applied along the direction _y. As explained above, the minimization of the interaction energy between the director and the external magnetic field stimulates a director torsion in order to put both parallel. But the nematic material is an elastic medium which is not free to rotate. The director is bounded to the sample's surface and, at these points, it cannot turn. As stressed before, in this situation a competition between the magnetic field and the elastic energy arises. In fact, in the bulk, the magnetic field tends to align the director along its direction, whereas the elastic energy tends to produce an orientation consistent with its orientation at the boundaries of the sample. When the value of magnetic field is greater than a critical value H_c the director begins to incline. For a value of the magnetic field below H_c there is no observable distortion in the nematic material. But when the value of the magnetic field overcomes H_c it is observed the arising of textures in the sample, denoting that away from edges the director has complied to the magnetic torque. This critical point is the Frèedericksz threshold H_c.

There are two ways of approaching this critical point, i.e, from below, when H < H_c, and from above, when H > H_c. In the first situation there is no director bending and a static approach seems to be enough to understand the Frèedericksz threshold. In the second situation, as explained above, a complex dynamical cooperative phenomenon appears. It is responsible for the richness of nematic textures found above the Frèedericksz threshold. In order to describe this director bending, and the subsequent matter flow, the so-called Eriksen-Leslie-Parodi (ELP) approach [14-18] will be used. In this picture the NLC dynamics is given by the anisotropic version of the Navier-Stokes equation[19]

where r is the density of the system, V_a is the a- component of velocity, p is the pressure, and s_ba is the associated anisotropic stress tensor[20, 21]. Notice that the stress tensor is dependent on variables like the velocity of the fluid, the bending of the director q, and the director time variation rate .

The equation of motion for the director, in the ELP approach, assumes the form[20, 21]

where the inertial terms were not considered, g₁ and g₂ are the shear torque coefficients, and, as usual, the fluid is considered incompressible.

Since the external magnetic field is applied along the direction perpendicular to the initial orientation of the director, we can suppose that the director will always remain in the plane defined by the magnetic field direction and the initial orientation of the director[3], that is

where q(x, y, z) is the angle between the director and the direction. Furthermore, in order to further simplify these equations, the motion along the _z direction will not be considered because the components describing the motion of the nematic fluid along the and _y directions are sufficient to describe the walls phenomenology[3]. The pressure p can be eliminated from these equations by subtracting, in the Navier-Stokes equation, the term describing the motion along the _y direction from the one describing the motion along the direction. In this manner one obtains

The approximations made so far are not enough to give a solution to Eq. ( 4). The usual way to proceed is to restrict the analysis to the linear terms of the viscosity tensor. This procedure overshadow the walls universal character and, in our approach, we tried to maintain it. Consequently, our study was restricted to those regions of the sample where the velocity component V_y is dominant, and the fact that the director oscillatory character is present, since the beginning of the walls creation, was used. This allows us to assume that, even at these initial moments, there are a set of lines for which ¶_xq = 0. Furthermore, the one-dimensional character of these structures requires that, once fixed x, the director would be constant along the direction of the external magnetic field, that is ¶_yq = 0. Finally, a change of scales given by[4]

is introduced.

Therefore, the equations governing the director's bending becomes

where the following definitions have been used: k = 2p/l, with l being the walls length, , and t = (g₁/c_aH_c²)t. Furthermore, in Eq. (6) one has

with

In Eq. (8) h₁, h₂, h₃, h₁₂, and g₁, are the five independent Miesowicz viscosity coefficients[1, 20, 21]. Observe that due to the dependence of A_i, i = 1,...,5 on q, Eq. (6) is yet strongly non-linear.

It is important to stress that Eq. (6) gives the time rate of growing of the director only at those regions where it achieves its greatest bending. Despite of this limitation, this equation has some advantages. It can be easily numerically integrated and the non linear structure of the phenomenon is maintained; its linear limit gives the Lonberg result [3]. Furthermore, it shows, at the left hand side, the rate of variation of the amplitude ¶_tq and, at the right hand side, its dependence on 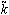², q, and on the viscosity coefficients. According Lonberg et al. [3] the preferred is determined when its value giving the maximum to ¶_tq is achieved.

III The elastic corresponding states

From Eq. (2) one observes that when the motion of the nematic material that gives rise to the walls stops, the resulting structure is described by

It is easily shown that this equation follows from an elastic energy given by

where K₁₁, K₂₂, and K₃₃ are the elastic constants of splay, twist, and bend, respectively and V is the volume of the sample. Therefore, as Eq. (9) describes elastic structures, once formed the walls have to be considered as solutions of Eq. (9).

Since, on the other hand, the walls are periodic structures extending along the direction, the simplest configuration for the director along the _y and _z directions[4] will be assumed, namely

where the field h(x) describes the configuration of the director along the direction.

With these information in mind, and using the change of scale defined in Eq. (5), the free energy given by Eq. (10) can be rewritten in the form

where

In Eqs. (12,13) is the re-scaled sample length along the direction, , and .

As it has been stressed in a previous work[22], all the material parameters characterizing any particular NLC sample have been put aside. Therefore, one may hope that all static configuration of the NLC can be reduced to a line of corresponding states[10], described by the universal (free from material parameters) equation

When the scaling laws, Eq. (5), were applied to experimental data of different samples it was verified that, indeed, all measured points extended along the same universal line[22]. In Fig. 3 we show the measured points for some different experimental data. It was used rationalized units for the magnetic field in order to obtain the same scale. Observe that the points are spread and there is not any evident correlation among them. But, when the relations given in Eq. (5) are used the result shown in Fig. 4 is found. The continuous line is to be considered only as an eye's guiding.

Figure 3.
Measured points of (2d/l)² vs the reduced magnetic field h = H/H_c. l is the length of the walls periodicity as observed in the microscope and d is the thickness of the slab.

These findings are unexpected. Only the elastic parameter were used in the scaling given in Eq. (5), and these properties are not the sole responsible by the emergence and geometry of the walls. As shown in the preceding section the walls resulted from the combined action of the external field on the director and the matter movement. Therefore, it may expected that some dynamical parameters, such as the viscosity coefficients, will contribute to the determination of the geometrical properties of the walls. Even being the measurements of the walls parameters made in a static condition, the constants of integration of Eq. (14) are fixed during the fluid flow that gives rise to the walls. Therefore, it is expected to find in the walls geometry some information about the physical conditions prevailing in its origin. Nevertheless, as it is observed in Fig. 4, the static parameters, through the appropriate scaling presented above, are enough to put the experimental data along a single curve. The success of the scaling laws in reducing these experimental data to a universal line seems to indicate that there is also some unknown universality in the dynamical motion that built the walls. Below, a sketch of this demonstration will be given (see ref.[11] for details).

Figure 4.
The points of Fig. 3 scaled in such a way that all of them stay along the same line. As demonstrated in the text, contrarily to the expected, the parameters of the scaling only depend on the elastic constants.

In order to accomplish this task, we look for some parameters characterizing the NLC media and use them in Eq. (6). These NLC compounds, their viscosities coefficients, and the references from where they were obtained are displayed in Table 1.

Table 1:
Viscosities in 10^-3kgm^-1s, the ratio K₃₃/K₂₂, and the references from where these data were obtained for several NLC compounds. The symbol "?'' means that the corresponding value is unknown by the authors. The values of the K₃₃/K₂₂ accompanied by (?) are attributed. The compound named as "mixture '' was found in ref. [23] and is a 1:1:1 molar mixture of HBAB with p-n- butoxybenzylidene -p- aminobenzonitrile and p-n-octanoyloxybeziledene -p- aminobenzonitrile.

To each of these compounds the values of

² as function of q that makes Eq. (14) maximum have been numerically found. These are the preferred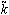 ². A remarkable aspect of this result, shown in Fig. 5, is that for samples as distinct as the ones shown in the Table 1 the curves of the preferred 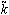² as a function of q are not so different. Only the elastic constant have been scaled and the viscosity coefficients, that are explicitly present in Eq. (14) seemto play a not important role in this picture. Therefore, it remains to explain why the viscosity coefficients become absent in the preferred 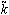² curve.

Figure 5.

First of all, observe that the viscosity coefficients appear, in Eq. ( 14), in the factor R(

²,h_i,g,q) which, with some labour can be rewritten as

where

and ; ; are reduced viscosities. Table 2 shows the values of these reduced parameters

Table 2:
Reduced values of the viscosities

The reason for the coincidence of the preferred curves become clear in Eqs. (15), (16), and Table 2. It is not the absolute values of these viscosity coefficients that are important, but the relative ones. When compared with the dispersion of the Table 1, the relative values of the Table 2 are much more coincident. For example, in Table 1 the values for h₁ range from 9.3 to 103 10^-3kgm^-1s. Meanwhile, in Table 2 ₁ ranges from 2.60 to 2.96. The small variation of the relative values of the viscosity coefficients is the responsible for the corresponding states of the NLC walls.

It is important to emphasize that although the relative values of the viscosity coefficients are much more coincident than the absolute ones, they are not exactly the same (see table 2). Therefore, one can expect to find the presence of the viscosity coefficients in the macroscopic walls parameters through a little effect. However, the present data for the walls periodicity l are not sufficient to reveal it and we can affirm that, if observed, such effect will be very small. It should be noticed that even being not determined at the moment at which the matter flow begins, the value of l must be fixed when the bending of the director is small. When this condition is placed in Eq. (16) the parameters determining the preferred curve are given by that presented in the last two columns of Table 2.

Therefore, we observe that the key to understand the law of the corresponding states in the nematic state is the existence of an approximate constant ratio between the viscosity coefficients. As far as we know, the first report of such constant relation between the viscosity coefficients is found in the work of Kneppe et al.[12]. They found, examining their experimental data, some ad hoc laws connecting the values of the Miesowicz viscosity coefficients. They do not give any justification for the existence of this constant ratio. We believe that, as in the seminal work of Helfrich[29], it is related with the anisotropic shape of the nematic micelle.

IV The collapse of the magnetic walls

As it is well known, for magnetic fields far above the Frèedericksz threshold the walls tend to disappear[30, 31]. The basic mechanism for their destruction is the instability beginning at the moment in which the flux of matter[3] that gives rise to them stops. At this moment the extremely harmonic and periodic walls pattern begins an unstable phase after which all its one-dimensional and periodic regularity is lost.

Habitually unstable configurations are found in physical systems after the action of some transient force operating during a finite time interval [32, 33. While the transient action is working, the system goes to a configuration that, as soon as it vanishes, no longer has the least energy. In the walls case the transient force is given by the initial flux of the nematic material [3]. Of course, the fact that the walls do not have the least energy is a necessary, but not sufficient, condition to promote their instability. In fact, the fluid flow leads the system to a configuration that is an extremum of the energy but, as a simple elastic argument shows, it is not the configuration with the least energy[34]. But even not being in the ground state, the walls could be in a local minimum at which the system might remain indefinitely. We have shown that, as the experiments confirm, the walls configuration is indeed a local free energy maximum. In order to prove it, the second functional derivative of the free energy, around the walls configuration, was studied and it was shown that it is negative[13]. Nothing more than the oscillatory and one-dimensional character of the walls were assumed along that demonstration.

In order to fully appreciate the details of the walls wasting process, a wall profile, in which their geometrical parameters were shown, was constructed and exhibited in Fig. 6. This profile is described by three parameters: the walls amplitude j_o, the walls length l, and the walls form factor d. The parameter d, changing between 0 and 1, controls the form of the wall. The wall has two distinct regions[8]. In one of them (the w region) the director bends its orientation from one configuration to the symmetric one. The other region (the D region) describes a saturated portion of the director. The d value gives the fraction of each portion. When d® 1, the wall becomes a single sine function. On the other hand, when d® 0 the saturated region assumes the entire wall. One observes from Fig. 6 that D, given by

is a measure of the saturated portion of the wall. Furthermore, Eq. (14) has a conserved quantity [8,22,35]

which reflects the homogeneity of the system along the direction. C is a fixed number that exists only as long as the system remains one-dimensional. Therefore, its value at the point where h = 0 can be compared with its value at the region where ¶_xh = 0, giving

which shows that as long as the system in one-dimensional the parameters l, D, and j_o are not independent.

Figure 6.
Graphic representation of a typical wall. It is explicitly shown the saturated portion D/2, the bending portion dl/2, and the amplitude j_o. The irreversible exponential growing fluctuations act in such a way to reduce the amplitude j_o and the saturated portion D [13].

As we have already remarked, the cornerstone of the instability is the one-dimensional and oscillatory character of the walls. Therefore, the starting point of the walls decay is strongly connected to the breakdown of this character. The system has to abandon the one-dimensionality. The collapse of the walls begins with the destruction of this connection and these parameters evolve independently.

The collapse of the walls is dominated by the random fluctuations around it. The fluctuations commanding this unstable process are the ones with grasps the least energy. This principle will lead to an independent development of l, D, and j_o and it is easy, for example, to obtain the force between two neighbor walls[13] and to show that it is repulsive and decays with the inverse of the square of the wall's portion, w = l-D, where there is the director bending (see Figs. 2 and 6). That is, shorter is the bend portion, more repulsive is the force between the wall. Finally, the minimization of the fluctuations' energy led us to a similar conclusion for the wall's saturated portion D and amplitude j_o: they become shorter and shorter with time.

Since the sample is composed by a large number of walls, the repulsive force between them may be counterbalanced and the net result may be an equilibrium situation. However, there is no way to get a counterbalanced effect in the reduction of the walls saturated portion D or in the reduction of the walls amplitude j_o. Therefore the reduction in D and j_o starts the destruction of the walls.

V Concluding remarks

In conclusion, let us stress some important points arising in our analysis of the physical properties of the walls. First of all we have shown that the family of periodic walls appearing above the Frèedericksz threshold can be reduced to a single physical situation through a law of corresponding states. This law is obtained by means of an appropriate choice of scale regarding the elastic constants and the critical field.

In a second moment we demonstrate that the physical reason for law of corresponding states lies in the behavior of the Miesowicz's viscosity coefficients. In fact, we observe that the key to understand this law in the nematic medium is the existence of an approximate constant ratio between the viscosity coefficients.

Finally, we would like to point out that our explanation for the collapse of the walls only takes care of the beginning of this process. It is experimentally observed that the walls evolve to closed structures having elliptical shape. Furthermore, it has to be stressed that even these closed elliptical walls are not stable. Frequently they disappear of the NLC sample. In fact, the minimization of the energy of the fluctuations leads to the destruction of the walls regular pattern by means of three mechanisms: a) a repulsive interaction; b) the reduction of the walls saturated portion; c) the reduction of the walls' amplitude. We believe that we have presented an important step towards a better understanding of these rich and complex non-linear phenomena in the NLC physics.

Acknowledgments

Financial support from the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) is acknowledged.

References

[1]
• P. G. de Gennes, The Physics of Liquid Crystals, (Clarendon Press, Oxford, 2nd edition, 1993).
[2]
• E. Guyon, R. Meyer and J. Salan, Mol. Cryst. Liq. Cryst. 54, 261 (1979).
[3]
• F. Lonberg, S. Fraden, A. J. Hurd and R. B. Meyer, Phys. Rev. Lett. 52, 1903 (1984).
[4]
• M. Simões, Phys. Rev. E 56, 3061 (1997).
[5]
• T. Kroin and A. M. Figueiredo Neto, Phys. Rev. A 36, 2987 (1987).
[6]
• T. Kroin, A. J. Palangana and A. M. Figueiredo Neto, Phys. Rev. A 39, 5373 (1989).
[7]
• A. J. Palangana, L. R. Evangelista and A. K. Zvezdin, Phys. Lett. A 200, 56 (1995) .
[8]
• M. Simões, A. J. Palangana and L. R. Evangelista. Phys. Rev. E 54, 3765 (1996).
[9]
• P. A. Santoro, A. J. Palangana, M. Simões, Phys. Lett. A 243, 71 (1998).
[10]
• H. E. Stanley, Introduction to Phase Transitions and Critical Phenomena, (Claredon Press, Oxford, 1971).
[11]
• M. Simões, A. A. Arrotéia, Phys. Rev. E (1998) ( in press)
[12]
• H. Kneppe, F. Scheneider, N. K. Sharma, Ber. Bunsenges Phys. Chem. 85, 784 (1981).
[13]
• M. Simões, A. J. Palangana, F. C. Cardoso, Phys. Rev. E 58, 2011 (1998).
[14]
• J. L. Ericksen, Arch. Ratl. Mech. Anal. 4, 231 (1960); 9, 371 (1962).
[15]
• F. M. Leslie, Quart. J. Mech. Appl. Math. 19 357 (1966).
[16]
• O. Parodi, J. Physique (Paris) 31, 581 (1970).
[17]
• W. C. Oseen, Trans. Faraday Soc. 29, 883 (1933).
[18]
• F. C. Frank, Discussions Faraday Soc. 25, 19 (1958).
[19]
• L.D. Landau, E. M. Lifshitz. Fluid Mechanics, (Butterworth-Heinemann, Oxford, 1995).
[20]
• W. H. de Jeu. Physical properties of liquid crystalline materials, (Gordon and Breach, New York, 1979).
[21]
• G. Vertogen, W. H. de Jeu. Thermotropic Liquid Crystals, Fundamentals, (Springer-Verlag, Berlin, 1988).
[22]
• A.J. Palangana, M. Simões, L. R. Evangelista, A. A. Arroteia. Phys. Rev. E. 56, 4282 (1997).
[23]
• C. H. Gahwiller, Mol. Cryst. Liq. Cryst. 20, 301 (1972).
[24]
• W. H. de Jeu, W. A. P. Claassen, A. M. J. Spruijt, Mol. Cryst. Liq. Cryst. 37, 269 (1976).
[25]
• M. G. Kim, S. Park, Sr. M. Cooper, S.V. Letcher, Mol. Cryst. Liq. Cryst. 36, 143 (1976).
[26]
• N. V. Madhusudana, P. P. Karat, S. Chandrasekhar, Pramona Suppl. 1, 225 (1975).
[27]
• G. P. Chen, H. Takezoe, A. Fukuda. Liquid Crystal, 5, 347 (1989).
[28]
• Chmielewski, Mol. Cryst. Liq. Cryst. 132 339 (1986).
[29]
• W. Helfrich, J. Chem. Phys. 52, 100 (1969); 53, 2267 (1970); 56, 3187 (1972).
[30]
• F. Brochard , J. Phys. (Paris) 33, 607 (1972).
[31]
• L. Léger , Mol. Cryst. Liq. Cryst. 24, 33 (1973).
[32]
• R. Kubo, M. Toda, N. Hashitsume. Statistical Physics II, Nonequilibrium Statistical Mechanics, (Springer-Verlag, Berlin, 1991).
[33]
• D. Chandler. Introduction to Modern Statistical Mechanics, (Oxford University Press, New York, 1987).
[34]
• E. A. Oliveira, G. Barbero and A. M. Figueiredo Neto, Phys. Rev. E 54, 5830 (1996).
[35]
• M. Simões, A. J. Palangana and L. R. Evangelista, Phys. Rev. E 56, 7326 (1997).

Publication Dates

• Publication in this collection
  26 Aug 1999
• Date of issue
  Dec 1998

History

• Received
  26 Oct 1998