Resumen
La expansión del proyecto Club GeoGebra (CG) en las instituciones de educación media, en Venezuela, demanda el diseño de oportunidades formativas para los profesores (promotores del CG) que se integran cada año. Una componente esencial del diseño es el saber necesario para gestionar los procesos de modelación por los que transitan los alumnos del CG cuando elaboran simuladores. Para develar esta componente, realizamos un estudio en el que identificamos y describimos los saberes para la gestión del trabajo matemático reconocidos por un grupo de promotores del CG que discuten las prácticas de resolución de tareas de construcción con GeoGebra de un colega y sus alumnos. Las discusiones fueron registradas en vídeo. Mediante una técnica de análisis interpretativo, se identificaron tres saberes necesarios para gestionar el trabajo matemático: saber cómo analizar la inconsistencia de una construcción, saber cómo comunicar a otros una técnica de construcción y saber cómo anticipar una técnica antes de ser empleada. Los resultados sugieren que estos saberes se encuentran enraizados en la experiencia práctica de los promotores del CG. Sin embargo, el reconocimiento de tales saberes no solo tiene su lado subjetivo, sino también un lado cultural que discutimos al final del artículo.
Palabras clave:
Saberes docentes; Simuladores con software dinámico; Uso de vídeos; Análisis interpretativo
Abstract
Club GeoGebra (CG) project expansion in Venezuela high schools demands to design each year training opportunities for new teachers (CG promoter). An essential component of the design is the knowledge related with modelling processes that happen when the CG students develop simulators. To unveil this component, we conducted a study in which we identify and describe the knowledge for the management of mathematical work recognized by a group of CG promoters. These teachers discussed the practices of solving construction tasks with GeoGebra of a colleague and his students, while their discussions were recorded on video. Using an interpretative analysis technique, we identified three types of knowledge needed to manage the mathematical work: knowledge of how to analyze a construction inconsistency, knowledge of how to communicate a construction technique and knowledge of how to anticipate the technique before it is used. Our results suggest that the knowledges are rooted in the practical experience of the CG promoters. However, the recognition of such knowledge not only has its subjective side, but also a cultural side that we discussed at the end of the article.
Keywords:
Teaching knowledge; Dynamical software simulators; Use of videos; Interpretative analysis
1 Introducción
El Club GeoGebra es un proyecto educativo que se implementa en algunas instituciones públicas de educación media del Estado Zulia, en Venezuela, desde el año escolar 2013-2014. El objetivo de este proyecto es contribuir con el aprendizaje de la matemática y ciencias afines, a través de procesos de modelación de fenómenos reales que son mediados por tecnologías digitales. Básicamente, los clubes GeoGebra son espacios en los que se reúnen alumnos de diferentes edades (doce a diecisiete años) y profesores de matemática (quienes reciben el nombre de promotores) para elaborar simuladores con GeoGebra de una forma libre y voluntaria.
Los resultados del trabajo conjunto de alumnos y promotores de los clubes han mostrado las bondades de la elaboración de simuladores con GeoGebra para el desarrollo de las capacidades matemáticas de estos sujetos, en un ambiente mediado por el uso de un software de geometría dinámica (GUTIÉRREZ; PRIETO; ORTIZ, 2017GUTIÉRREZ, R.; PRIETO, J. L.; ORTIZ, J. Matematización y trabajo matemático en la elaboración de simuladores con GeoGebra. Educación Matemática, México D. F., v. 29, n. 2, p. 37-68, 2017.; PRIETO; GUTIERREZ, 2015PRIETO, J. L.; GUTIÉRREZ, R. E. (Comps.). Memorias del I Encuentro de Clubes GeoGebra del Estado Zulia. Maracaibo: Aprender en Red, 2015., 2016PRIETO, J. L.; GUTIÉRREZ, R. E. (Comps.). Memorias del II Encuentro de Clubes GeoGebra del Estado Zulia. Maracaibo: Aprender en Red, 2016., 2017; RUBIO; PRIETO; ORTIZ, 2016RUBIO, L.; PRIETO, J. L.; ORTIZ, J. La matemática en la simulación con GeoGebra. Una experiencia con el movimiento en caída libre. International Journal of Educational Research and Innovation, Madrid, v. 2, n. 1, p. 90-111, 2016.; SÁNCHEZ; PRIETO, 2017SÁNCHEZ, I.; PRIETO, J. L. Características de las prácticas matemáticas en la elaboración de simuladores con GeoGebra. Números Revista de Didáctica de las Matemáticas, Tenerife, v. 96, p. 79-101, 2017.). Al mismo tiempo, la difusión de estos resultados ha favorecido la aceptación del proyecto entre profesores e investigadores, dentro y fuera del país, quienes ven necesario incrementar el número de instituciones escolares atendidas en cada año por el proyecto Club GeoGebra.
Para esto, es necesario formar a los nuevos promotores para enfrentar las demandas de una enseñanza situada en un ambiente de elaboración de simuladores con GeoGebra. Evidentemente, esta formación puede materializarse a través del diseño de un programa formativo cuya particularidad nos obliga a pensar en: ¿cuáles deben ser los contenidos de ese programa? ¿qué elementos pueden aportar las experiencias de enseñanza de los promotores al diseño de la formación? ¿conviene reconocer estas experiencias como válidas y necesarias para la formación de los nuevos promotores?
La presente investigación sirve de preámbulo al diseño de una formación para la enseñanza de tópicos de geometría (y demás dominios de la matemática) en ambientes de elaboración de simuladores con GeoGebra. En particular, centramos la atención en una de las componentes del diseño, relacionada con los saberes necesarios para gestionar el trabajo matemático de los alumnos del Club GeoGebra.
2 Una cuestión problemática alrededor de los saberes docentes
Durante los últimos treinta años, los estudios sobre los saberes de los profesores de matemática se han incrementado considerablemente (PONTE; CHAPMAN, 2006PONTE, J. P.; CHAPMAN, O. Mathematics teachers' knowledge and practices. En: GUTIÉRREZ, A.; BOERO, P. (Ed.). Handbook of Research on the Psychology of Mathematics Education: past, present and future. Rotterdam: Sense Publishers, 2006. p. 461-494.; REIS; AFFONSO, 2007REIS, M. E. T.; AFFONSO, S. A. B. Os programas formais de formação continuada e sua relação com os saberes docente. Revista de Educação do Curso de Pedagogia do Campus Avançado de Jataí da Universidade Federal de Goiás, Jataí, v. 1, n.3, p. 1-18, 2007.). A pesar de que estas investigaciones han permitido conocer las carencias, tipología, naturaleza y desarrollo de estos saberes (FIORENTINI; SOUZA; MELO, 1998FIORENTINI, D.; SOUZA, A.; MELO, G. A. Saberes docentes: um desafio para académicos e práticos. En: GERALDI, C. M. G.; FIORENTINI, D.; PEREIRA, E. M. (Org.). Cartografias do trabalho docente: professor (a)-pesquisador (a). Campinas: ALB e Mercado de Letras, 1998. p. 307-335.), la mayoría ha puesto su atención solo en los saberes disciplinares y curriculares integrados a la formación del profesorado, restando importancia a esos saberes específicos provenientes de la experiencia práctica con los alumnos (TARDIF, 2002TARDIF, M. Los saberes del docente y su desarrollo profesional. Madrid: Narcea, 2002.).
En este sentido, Tardif (2002)TARDIF, M. Los saberes del docente y su desarrollo profesional. Madrid: Narcea, 2002., sostiene que la lógica de trabajo que impera en la cultura científico-educativa moderna ha privilegiado una relación de los profesores con los saberes que les reduce a meros transmisores o portadores de información, reservando el acto de producción de conocimiento únicamente a los teóricos e investigadores de la educación.
Frente a esta realidad, se hace necesario cambiar la visión del profesor como un sujeto carente de conocimiento e incapaz de producir innovaciones en el aula, en otra percepción que acepte su condición de “profesional que posee un saber especial, el cual ha sido construido reflexivamente en situaciones complejas y, muchas veces, adversas y deshumanas” (FIORENTINI; NACARATO; PINTO, 1999FIORENTINI, D; NACARATO, A.; PINTO, R. A. Saberes da experiência docente em matemática e educação continuada. Quadrante Revista Teórica e de Investigação, Lisboa, v. 8, n. 1-2, p. 33-60, 1999., p. 19). Esta transformación necesaria pone de manifiesto la importancia de los saberes prácticos de los profesores como núcleo vital de los saberes docentes (TARDIF, 2002TARDIF, M. Los saberes del docente y su desarrollo profesional. Madrid: Narcea, 2002.) y punto de partida de la formación permanente del profesorado de matemática (REIS; AFFONSO, 2007REIS, M. E. T.; AFFONSO, S. A. B. Os programas formais de formação continuada e sua relação com os saberes docente. Revista de Educação do Curso de Pedagogia do Campus Avançado de Jataí da Universidade Federal de Goiás, Jataí, v. 1, n.3, p. 1-18, 2007.).
En relación con esto último, Tardif (2002)TARDIF, M. Los saberes del docente y su desarrollo profesional. Madrid: Narcea, 2002. afirma que el grado de desarrollo y sistematización que puede alcanzar un determinado saber docente (incluyendo al saber práctico) crea condiciones para que éste sea integrado a los procesos de formación profesional institucionalizados.
En lo que respecta a la enseñanza de la geometría, González-López (2001GONZÁLEZ-LÓPEZ, M. J. La Gestión de la Clase de Geometría utilizando Sistemas de Geometría Dinámica. En: GÓMEZ, P.; RICO, L. (Eds.). Iniciación a la investigación en Didáctica de la Matemática. Homenaje al profesor Mauricio Castro. Granada: Universidad de Granada, 2001. p. 277-290., p. 285) propone una serie de actuaciones posibles de los profesores durante el desarrollo de clases que involucran el uso de un software de geometría dinámica, entre las que destacan: (i) invitar a la predicción de resultados, (ii) provocar la reflexión sobre el tipo o tipos de representación que entran en juego, y (iii) ayudar a la interpretación de relaciones entre lo visual y lo formal. Considerando lo anterior, el foco de nuestra investigación se sitúa en los saberes de la gestión del trabajo matemático que se revelan en las prácticas de alumnos y promotores en situación de elaboración de simuladores con GeoGebra.
Particularmente, el estudio identifica y describe estos saberes con el fin de formalizarlos e integrarlos progresivamente a una propuesta de formación docente online, dirigida a profesores de matemática con interés en sumarse al Club GeoGebra como promotores. En el siguiente apartado, damos a conocer la actividad en la cual se movilizan estos saberes.
3 Elaboración de simuladores con GeoGebra
Recientemente, se han realizado algunas investigaciones que dan cuenta de las implicaciones del uso simuladores y juegos de vídeo en clases de matemática (GONZÁLEZ; MOLINA; SÁNCHEZ, 2014GONZÁLEZ, A. G.; MOLINA, J. G.; SÁNCHEZ, M. La matemática nunca deja de ser un juego: investigaciones sobre los efectos del uso de juegos en la enseñanza de las matemáticas. Educación Matemática, México D. F., v. 26, n. 3, p. 109-133, 2014.; GREEFRATH, 2011GREEFRATH, G. Using technologies: new possibilities of teaching and learning modelling– Overview. En: KAISER, G.; BLUM, W.; BORROMEO, R.; STILLMAN, G. (Eds.). Trends in the teaching and learning of mathematical modelling. Dordrecht: Springer, 2011. p. 301–304.). En el caso de los simuladores, algunos estudios han reportado el potencial de estos recursos para el desarrollo de las capacidades de visualización y experimentación de los alumnos, por medio de la manipulación de variables y parámetros asociados a modelos computacionales que representan determinados fenómenos de la realidad (CLARK et al., 2009CLARK, D.; NELSON, B.; SENGUPTA, P.; D'ANGELO, C. Rethinking science learning through digital games and simulations: Genres, examples, and evidence. Washington DC: National Research Council, 2009.; PUGNALONI, 2008PUGNALONI, L. A. Los simuladores. El papel de la simulación en la ciencia. Ciencia Hoy, Buenos Aires, v. 105, n. 1, p. 27-34, 2008.). En el ámbito educativo, un simulador computacional1 1 Algunos ejemplos de simuladores computacionales se pueden consultar en: https://phet.colorado.edu/es/. es el producto de la representación de un proceso o fenómeno (natural o artificial), por medio de modelos computacionales elaborados con la ayuda de determinadas herramientas tecnológicas (SÁNCHEZ; PRIETO, 2017SÁNCHEZ, I.; PRIETO, J. L. Características de las prácticas matemáticas en la elaboración de simuladores con GeoGebra. Números Revista de Didáctica de las Matemáticas, Tenerife, v. 96, p. 79-101, 2017.).
A pesar del creciente interés de los profesores en el uso de simuladores en clases de matemática, coincidimos con Artigue (2016)ARTIGUE, M. Aportes de la integración de tecnologías en la sala de clase de matemática, 2016. Disponible en: <https://www.youtube.com/watch?v=6v-DErde1GE&t=316s>. Acceso en: 12 oct. 2017.
https://www.youtube.com/watch?v=6v-DErde...
en que la educación del siglo XXI debe permitir a los ciudadanos pasar de ser consumidores a ser productores de la tecnología, razón por lo cual vemos necesario explorar actividades alternativas como la elaboración de simuladores computacionales y conocer sus implicaciones en los procesos de enseñanza y aprendizaje.
En el marco del proyecto Club GeoGebra, la elaboración de simuladores es una actividad de producción de modelos reales, matemáticos y computacionales que representan las formas, dimensiones y movimientos característicos de ciertos fenómenos2 2 Los fenómenos seleccionados por alumnos de los clubes GeoGebra han sido reportados en Prieto y Gutiérrez (2015, 2016, 2017). , relacionados, en su mayoría, con la variación en el estado de los objetos de la naturaleza o el funcionamiento parcial o total de un sistema mecánico (máquinas simples). Elegido el fenómeno, el modelo computacional correspondiente se obtiene mediante la resolución de un conjunto de tareas de simulación que garantizan la adecuada representación de esta realidad en la interfaz del GeoGebra (RUBIO; PRIETO; ORTIZ, 2016RUBIO, L.; PRIETO, J. L.; ORTIZ, J. La matemática en la simulación con GeoGebra. Una experiencia con el movimiento en caída libre. International Journal of Educational Research and Innovation, Madrid, v. 2, n. 1, p. 90-111, 2016.).
La resolución de estas tareas pone en marcha un ciclo de modelación matemática propio de la elaboración de simuladores con GeoGebra que hemos reportado en trabajos previos, que han servido para situar esta actividad dentro de un panorama general de prácticas de modelación mediadas por tecnologías digitales (GUTIÉRREZ, 2017GUTIÉRREZ, R. Elaboración de simuladores con GeoGebra. Una actividad de modelación matemática mediada por tecnologías digitales. En: PRIETO, J. L.; GUTIÉRREZ, R. E. (Comp.). Memorias del III Encuentro de Clubes GeoGebra del Estado Zulia. Maracaibo: Aprender en Red, 2017. p. 234-252.; GUTIÉRREZ; PRIETO; ORTIZ, 2017GUTIÉRREZ, R.; PRIETO, J. L.; ORTIZ, J. Matematización y trabajo matemático en la elaboración de simuladores con GeoGebra. Educación Matemática, México D. F., v. 29, n. 2, p. 37-68, 2017.; PRIETO, 2017PRIETO, J. L. Proyectos de simulación con GeoGebra: una estrategia del desarrollo del pensamiento científico desde el servicio comunitario. Trabajo de ascenso (Asociado) – Facultad de Humanidades y Educación, Universidad del Zulia, Maracaibo, 2017.). Como se sabe, la modelación en educación matemática y, particularmente, aquella que es mediada por tecnologías digitales representa un tópico de gran relevancia actual en nuestro campo (GREEFRATH, 2011GREEFRATH, G. Using technologies: new possibilities of teaching and learning modelling– Overview. En: KAISER, G.; BLUM, W.; BORROMEO, R.; STILLMAN, G. (Eds.). Trends in the teaching and learning of mathematical modelling. Dordrecht: Springer, 2011. p. 301–304.). El ciclo en cuestión está compuesto por cuatro etapas y cuatro procesos cognitivos (Figura 1).
La resolución de cada tarea de simulación comienza con la elaboración de un dibujo a mano alzada de esa parte del fenómeno mencionada en el enunciado. Este dibujo recibe el nombre de boceto. En cuanto entidad material, el boceto adquiere un significado en la realidad concreta que se alimenta de la propia experiencia con el fenómeno o de información proveniente de Internet (PRIETO, 2017PRIETO, J. L. Proyectos de simulación con GeoGebra: una estrategia del desarrollo del pensamiento científico desde el servicio comunitario. Trabajo de ascenso (Asociado) – Facultad de Humanidades y Educación, Universidad del Zulia, Maracaibo, 2017.). El significado otorgado al boceto da forma a un modelo real que es una de las referencias básicas para la toma de decisiones durante la elaboración del simulador.
A medida que avanzan en la actividad, alumnos y promotores transforman los significados otorgados al modelo real como consecuencia de un proceso de matematización, que consiste en identificar aquellos objetos geométricos representativos de las cualidades de forma, tamaño y posición de la realidad bocetada. En palabras de Hershkowitz (1998HERSHKOWITZ, R. About reasoning in geometry. En: MAMMANA C.; VILLANI, V. (Ed.). Perspectives on the Teaching of Geometry for the 21th Century. Dordrecht: Kluwer Academic Publishers, 1998. p. 29-83., p. 32), la matematización en geometría es “un proceso de organización por medio del cual los elementos de un contexto son transformados en objetos geométricos y relaciones […]”. En nuestro caso, matematizar implica traducir el boceto en términos geométricos y, de esta manera, obtener un modelo matemático fundamental para la resolución de la tarea de simulación.
El nuevo modelo está determinado por el conjunto de objetos geométricos que, desde un punto de vista subjetivo, garantizarían la representación del boceto en la vista gráfica del GeoGebra. La Figura 2 muestra el boceto de un alumno del Club GeoGebra, sobre el cual este señala los objetos geométricos que componen a su modelo matemático correspondiente a una parte de un brazo robótico con el GeoGebra.
El producto de la matematización es un boceto que representa un significante de varios referentes teóricos de la geometría euclidiana (LABORDE, 1997LABORDE, C. Cabri Geómetra o una nueva relación con la geometría. En: PUIG L. (Ed.). Investigar y enseñar: variedades de la educación matemática. Madrid: Una Empresa Docente, 1997. p. 33-48.), por lo tanto, el dibujo en papel llega a ser un modelo de los objetos geométricos que representan al fenómeno y ofrecen un campo de experimentación gráfica posible de explorar. La necesidad de construir estos objetos con el GeoGebra es reflejada en un conjunto de tareas de construcción (LABORDE, 1997LABORDE, C. Cabri Geómetra o una nueva relación con la geometría. En: PUIG L. (Ed.). Investigar y enseñar: variedades de la educación matemática. Madrid: Una Empresa Docente, 1997. p. 33-48.) que se formulan y organizan en una secuencia para responder a determinada tarea de simulación. En este momento, el proceso de matematización se da por concluido.
La Figura 3 muestra ejemplos de este tipo de tareas de construcción.
Un proceso como el mostrado en la Figura 3 se repite para cada una de las tareas de simulación del mismo proyecto.
Para transformar el modelo matemático en el modelo computacional correspondiente, los alumnos se disponen a trabajar matemáticamente, esto es, a resolver las tareas de construcción de una misma tarea de simulación. Durante la resolución de estas tareas, los alumnos producen y reproducen formas codificadas de actuar y reflexionar geométricamente, que son mediadas por las herramientas del GeoGebra y la teoría geométrica subyacente. El proceso se repite para cada tarea de simulación del proyecto, lo que da lugar a una serie de dibujos dinámicos que se diferencian por su relación con las tareas de construcción, simulación y el proyecto en su conjunto.
Por dibujo dinámico se entiende aquel creado en un ambiente de geometría dinámica, de manera que “conserve ciertas propiedades espaciales impuestas cuando se desplace por uno de los puntos básicos del dibujo” (LABORDE, 1997LABORDE, C. Cabri Geómetra o una nueva relación con la geometría. En: PUIG L. (Ed.). Investigar y enseñar: variedades de la educación matemática. Madrid: Una Empresa Docente, 1997. p. 33-48., p. 42). Un primer tipo de dibujo dinámico se obtiene al resolver una tarea de construcción, independientemente del lugar que ésta ocupe en la secuencia. Un segundo tipo de dibujo se corresponde con el conjunto de todos los dibujos dinámicos que son el producto de las tareas de construcción de una misma secuencia. Al ser la respuesta a una tarea de simulación, este dibujo recibe el nombre de modelo computacional (Figura 4). El tercer tipo de dibujo es aquel formado por el conjunto de modelos computacionales que dan forma y sentido al simulador.
Indistintamente del tipo de dibujo dinámico que se obtenga, su producción demanda la comunicación al GeoGebra de un procedimiento geométrico de construcción que llamamos técnica (SÁNCHEZ, 2017SÁNCHEZ, I. Las prácticas matemáticas en la elaboración de simuladores con GeoGebra. 2017. 113. Tesis (Maestría en Matemática Mención Docencia) – Posgrado de la Facultad de Humanidades y Educación, Universidad del Zulia, Maracaibo, 2017.). En condiciones ideales, las técnicas de construcción deberían producirse a partir de las relaciones establecidas entre las propiedades espaciales del dibujo geométrico en papel y las propiedades geométricas del objeto matemático que éste intenta modelar. Sin embargo, en ocasiones, la percepción visual interfiere en el establecimiento de estas relaciones, sobre todo cuando no se tiene un conocimiento geométrico sólido que permita ir más allá de las primeras lecturas perceptivas (LABORDE, 1997LABORDE, C. Cabri Geómetra o una nueva relación con la geometría. En: PUIG L. (Ed.). Investigar y enseñar: variedades de la educación matemática. Madrid: Una Empresa Docente, 1997. p. 33-48.).
Es por esta razón que los alumnos que se inician en los clubes GeoGebra tienden a producir dibujos inconsistentes al resolver las tareas de construcción que se les presentan (SÁNCHEZ; PRIETO, 2017SÁNCHEZ, I.; PRIETO, J. L. Características de las prácticas matemáticas en la elaboración de simuladores con GeoGebra. Números Revista de Didáctica de las Matemáticas, Tenerife, v. 96, p. 79-101, 2017.; GUTIÉRREZ; PRIETO; ORTIZ, 2017GUTIÉRREZ, R.; PRIETO, J. L.; ORTIZ, J. Matematización y trabajo matemático en la elaboración de simuladores con GeoGebra. Educación Matemática, México D. F., v. 29, n. 2, p. 37-68, 2017.). Es importante destacar que estas inconsistencias son detectadas al aplicar al dibujo la prueba del arrastre, esto es, una modalidad de arrastre de los entornos dinámicos que consiste en: “mover un punto libre o semi-libre [dependiente] para ver si el dibujo mantiene las propiedades iniciales.
Si esto es así, entonces la figura pasa la prueba; en caso contrario, el dibujo no fue construido de acuerdo con las propiedades geométricas que se quería que tuviese” (ARZARELLO et al., 2002ARZARELLO, F.; OLIVERO, F.; PAOLA, D.; ROBUTTI, O. A cognitive analysis of dragging practices in Cabri environments. ZDM The International Journal of Mathematics Education, Berlin, v. 34, n. 3, p. 66-72, 2002., p. 67). Cuando el dibujo dinámico no pasa la prueba del arrastre, se dice que éste es inconsistente desde un punto de vista geométrico, puesto que la construcción pierde las propiedades con las que había sido dibujado originalmente.
Para Laborde (1997LABORDE, C. Cabri Geómetra o una nueva relación con la geometría. En: PUIG L. (Ed.). Investigar y enseñar: variedades de la educación matemática. Madrid: Una Empresa Docente, 1997. p. 33-48., p. 37), la sutileza entre lo espacial y lo geométrico puede superarse en la medida en que los sujetos tomen conciencia de estas relaciones al resolver “situaciones problema que traten de dibujos, en las que la geometría sea una herramienta eficaz de modelización”. En esta actividad, la manera en que los alumnos y el promotor utilizan las herramientas del GeoGebra para construir los dibujos puede condicionar el tipo de conexiones entre los niveles perceptual y teórico.
Sin embargo, es importante aclarar que el empleo per se de los ambientes dinámicos no garantiza el establecimiento de estas conexiones (ARZARELLO et al., 2002ARZARELLO, F.; OLIVERO, F.; PAOLA, D.; ROBUTTI, O. A cognitive analysis of dragging practices in Cabri environments. ZDM The International Journal of Mathematics Education, Berlin, v. 34, n. 3, p. 66-72, 2002.), por lo cual, vemos necesario que la resolución de las tareas de construcción, que enfrentan los alumnos del Club GeoGebra, se apoye en prácticas que resulten eficaces para vincular lo espacial y lo teórico en el trabajo matemático. Estas prácticas forman parte del repertorio de saberes docentes que emanan del proyecto y pueden ponerse a disposición de los profesores que deseen llevar a cabo esta labor. Aunque estos saberes resultan importantes para la enseñanza, en ocasiones, la propia dinámica de trabajo en las instituciones escolares puede hacer que éstos permanezcan ocultos e irreconocibles en la conciencia de los promotores.
4 Saberes en el proceso de trabajo matemático
Para esta investigación, asumimos que los saberes docentes tienen una naturaleza social, muy a pesar de que su existencia dependa del profesor (y de otros actores del proceso educativo), en cuanto individuo comprometido en una práctica concreta (TARDIF, 2002TARDIF, M. Los saberes del docente y su desarrollo profesional. Madrid: Narcea, 2002.). En oposición a la influencia que actualmente tienen las corrientes individualistas sobre las ideas de saber, conocimiento y aprendizaje, la Teoría de la Objetivación (TO) conceptualiza al saber no como una cosa que se trasmite o se construye, sino “como posibilidad, es decir, algo potencial que emerge de la actividad humana y que se imbrica en un proceso de movimiento – de devenir, para ser más precisos – para materializarse o expresarse en conocimiento” (RADFORD, 2017aRADFORD, L. Saber y conocimiento desde la perspectiva de la Teoría de la Objetivación. En: D'AMORE, B.; RADFORD, L. Enseñanza y aprendizaje de las matemáticas: problemas semióticos, epistemológicos y prácticos. Bogotá: Universidad Distrital Francisco José de Caldas, 2017a. p. 97-114., p. 100).
Esta manera de entender el saber revela dos aspectos importantes de la noción. Por un lado, el saber es la capacidad adquirida de hacer posible algo (la posibilidad) que no ha surgido en la realidad particular, por lo tanto, es una entidad general que no puede ser igualada con alguna de sus formas de realización concreta (RADFORD, 2017aRADFORD, L. Saber y conocimiento desde la perspectiva de la Teoría de la Objetivación. En: D'AMORE, B.; RADFORD, L. Enseñanza y aprendizaje de las matemáticas: problemas semióticos, epistemológicos y prácticos. Bogotá: Universidad Distrital Francisco José de Caldas, 2017a. p. 97-114.). Un ejemplo lo podemos ver al interior de la cultura de trabajo matemático en los clubes GeoGebra, en donde saber cómo resolver una tarea de construcción geométrica es una capacidad adquirida por los alumnos a lo largo de su experiencia.
Por otro lado, el saber es un sistema de reflexiones y acciones codificadas culturalmente, es decir, una forma ideal o prototípica de pensar y actuar, que es codificada en la memoria cultural como un patrón general (RADFORD, 2013aRADFORD, L. Three key concepts of the theory of objectification: Knowledge, knowing, and learning. Journal of Research in Mathematics Education, Reston, v. 2, n. 1, p. 7-44, 2013a.). Por consenso entre los promotores del proyecto, un modo prototípico de resolver tareas de construcción con GeoGebra comprende las siguientes etapas: a) los alumnos seleccionan la herramienta del software que permite construir el objeto geométrico mencionado en la tarea; b) identifican en la vista gráfica la presencia o ausencia de cada elemento requerido por la herramienta para construir el objeto en cuestión; c) construyen los elementos faltantes en base a relaciones entre las propiedades espaciales y teóricas del objeto a representar; d) aplican la herramienta (GUTIÉRREZ; PRIETO; ORTIZ, 2017GUTIÉRREZ, R.; PRIETO, J. L.; ORTIZ, J. Matematización y trabajo matemático en la elaboración de simuladores con GeoGebra. Educación Matemática, México D. F., v. 29, n. 2, p. 37-68, 2017.).
Para que el saber se ponga en movimiento, éste “tiene que mostrarse a sí mismo en la actividad a través de la cual adquiere su contenido” (RADFORD, 2017aRADFORD, L. Saber y conocimiento desde la perspectiva de la Teoría de la Objetivación. En: D'AMORE, B.; RADFORD, L. Enseñanza y aprendizaje de las matemáticas: problemas semióticos, epistemológicos y prácticos. Bogotá: Universidad Distrital Francisco José de Caldas, 2017a. p. 97-114., p. 108). En otras palabras, mediante la actividad es posible que el saber se materialice como un conocimiento que ha adquirido su propio contenido conceptual concreto, es decir, una forma singular desarrollada del saber (RADFORD, 2013aRADFORD, L. Three key concepts of the theory of objectification: Knowledge, knowing, and learning. Journal of Research in Mathematics Education, Reston, v. 2, n. 1, p. 7-44, 2013a.).
El ejemplo de la Figura 5 muestra una forma singular de construir un rectángulo, desarrollada por un alumno del Club GeoGebra (PELEY, 2016PELEY, S. La rotación en la simulación de un brazo robótico con el GeoGebra. En: PRIETO, J. L.; GUTIÉRREZ, R. E. (Comp.). Memorias del II Encuentro de Clubes GeoGebra del Estado Zulia. Maracaibo: Aprender en Red, 2016. p. 249-257.). Esta tarea era la quinta en la secuencia establecida por el joven para representar una parte de un brazo robótico (Figura 3). En su relato, el joven reconoce la existencia de dos vértices del rectángulo, y explica cómo determinó los dos vértices faltantes, antes de aplicar la herramienta Polígono.
En un sentido ontológico, la actividad puede ser vista como una labor conjunta, es decir, “una forma de vida, algo orgánico y sistémico, un evento creado por una búsqueda común – es decir, una búsqueda con otros– de la solución a un problema planteado, búsqueda que es al mismo tiempo cognitiva, emocional y ética” (RADFORD, 2017bRADFORD, L. Aprendizaje desde la perspectiva de la Teoría de la Objetivación. En: D'AMORE, B.; RADFORD, L. Enseñanza y aprendizaje de las matemáticas: problemas semióticos, epistemológicos y prácticos. Bogotá: Universidad Distrital Francisco José de Caldas, 2017b. p. 115-136., p. 125).
En el momento del trabajo matemático, la labor conjunta ocurre cuando alumnos y promotores resuelven juntos las tareas de construcción, produciendo así el modelo computacional que responde a determinada tarea de simulación. En esta labor, los profesores se comprometen en hacer que ciertos saberes (p. ej., saber cómo resolver tareas de construcción con GeoGebra) aparezcan en una forma conceptualmente robusta, involucrándose en las prácticas del aula, al mismo tiempo que reafirman su condición de docentes (RADFORD, 2013bRADFORD, L. Sumisión, alienación y (un poco de) esperanza: hacia una visión cultural, histórica, ética y política de la enseñanza de las matemáticas. En: RAMIREZ, A.; MORALES, Y. (Ed.). Memorias del I Congreso de Educación Matemática de América Central y El Caribe. Santo Domingo: REDUMATE, 2013b.).
Si bien, en medio de la actividad del aula, el profesor y los alumnos tienen diferencias en cuanto al nivel de familiaridad con los saberes matemáticos (el profesor, además, debe hacer que alguien aprenda ese saber), ambos trabajan hombro con hombro para lograr la materialización de esos saberes y su propia constitución (RADFORD; ROTH, 2011RADFORD, L.; ROTH, W.-M. Intercorporeality and ethical commitment: An activity perspective on classroom interaction. Educational Studies in Mathematics, Dordrecht, v. 77, n. 2-3, p. 227-245, 2011.). En otras palabras, mientras que los alumnos recurren a saberes matemáticos para resolver los problemas planteados en la clase, el profesor se apoya en estos mismos saberes y en otros más (útiles para la enseñanza) con el fin de hacer que sus alumnos aprendan matemática.
En los clubes GeoGebra, la actividad alrededor del trabajo matemático produce y reproduce distintos saberes que son del interés del promotor, ya que reflejan formas codificadas de pensar y actuar, geométricamente, en situaciones de producción de modelos computacionales. Durante la resolución de tareas de construcción con GeoGebra, los alumnos movilizan saberes geométricos y técnicos (vinculados al uso de las herramientas del software), mientras que el promotor se apoya en estos mismos saberes, y en otros más, que tienen sentido para la enseñanza en tanto provocan la toma de conciencia de los saberes geométricos. Son estos saberes de la enseñanza los que permiten que el promotor se afirme ante sus alumnos como un profesor de matemática (RADFORD, 2017cRADFORD, L. Ser, subjetividad y alienación. En: D'AMORE, B.; RADFORD, L. Enseñanza y aprendizaje de las matemáticas: problemas semióticos, epistemológicos y prácticos. Bogotá: Universidad Distrital Francisco José de Caldas, 2017c. p. 137-165.).
Como se sabe, la resolución de tareas de construcción en ambientes de geometría dinámica no es un proceso fácil, ni inmediato (LABORDE, 1997LABORDE, C. Cabri Geómetra o una nueva relación con la geometría. En: PUIG L. (Ed.). Investigar y enseñar: variedades de la educación matemática. Madrid: Una Empresa Docente, 1997. p. 33-48.). Por esta razón, los promotores idean formas de gestionar el trabajo matemático que les resultan útiles en circunstancias diversas como, por ejemplo, cuando los alumnos fallan en aplicar una técnica de construcción en sus primeras experiencias con el software. Aunque muchas veces las formas concretas de gestionar el trabajo matemático pueden ser ignoradas, o simplemente pasar desapercibidas, dificultando su posible transformación en un estado de conciencia crítica (FREIRE, 2002FREIRE, P. Concientización: teoría y práctica de una educación liberadora. Buenos Aires: Galerna, 2002.), también es cierto que estas experiencias pueden ser codificadas, dando como resultado la transformación de la propia enseñanza.
La codificación de estos saberes en la memoria cultural del proyecto Club GeoGebra requiere que los promotores tengan encuentros con estas formas prototípicas de resolver tareas de construcción geométricas, tanto durante el despliegue de las técnicas con sus alumnos (en el momento del trabajo matemático), como también en actividades en las que analizan las formas de proceder de sus colegas en ese momento.
Por ejemplo, al analizar registros en vídeo de prácticas de resolución de tareas de construcción geométrica surgidas en los clubes GeoGebra, es posible que los promotores tomen conciencia de los saberes necesarios para la gestión del trabajo matemático. Según Freire (2002FREIRE, P. Concientización: teoría y práctica de una educación liberadora. Buenos Aires: Galerna, 2002., p. 30), esta toma de conciencia implica que los profesores trasciendan la esfera espontánea de sus prácticas de enseñanza para llegar a una esfera crítica en la cual estas prácticas se convierten en objetos cognoscibles sobre los cuales se toman posiciones epistemológicas.
5 Metodología
El estudio se ubica dentro del paradigma de investigación cualitativa en educación matemática y, particularmente, entre los estudios de naturaleza descriptiva y reflexiva. Al respecto, Bogdan y Biklen (1994)BOGDAN, R.; BIKLEN, S. K. Investigação qualitativa em educação: uma introdução à teoria e aos métodos. Portugal: Porto, 1994. afirman que en las investigaciones cualitativas: (i) los datos son captados directamente del ambiente natural, (ii) los investigadores están preocupados más por los procesos que por los productos, y (iii) los resultados tienen una fuerte componente descriptiva.
5.1 Participantes y actividad
Los participantes de esta investigación fueron siete profesores de Matemática y Física (cuatro mujeres y tres hombres), quienes se desempeñaban como promotores del Club GeoGebra durante el año escolar 2016-2017. Cinco de estos profesores venían cumpliendo con el rol de promotores desde el inicio del proyecto, a finales del 2013. Al inicio del año escolar, los profesores se reunieron semanalmente, por espacio de cuatro horas, para tratar asuntos relacionados con el desarrollo de las fases del proyecto de clubes. Algunos de estos asuntos fueron: a) el plan de acción para los primeros encuentros de trabajo con los alumnos; b) la manera de llevar a cabo este plan; c) las características de los procesos de modelación a lo interior de la elaboración de simuladores; d) las formas de gestionar estos procesos por parte del promotor.
Con respecto a lo último, se dedicaron tres reuniones al análisis de la gestión del trabajo matemático en los clubes GeoGebra. El objeto de estas reuniones fue acercar a los profesores a determinadas formas de gestionar este proceso, en base a sus capacidades para identificar e interpretar prácticas de resolución de tareas de construcción con GeoGebra que favorecen la producción de los dibujos dinámicos y el consecuente aprendizaje.
Las reuniones fueron convocadas y dirigidas por el primer autor de este trabajo, quien, además, era promotor del proyecto en ese momento (en lo que sigue, nos referimos a este sujeto como promotor/investigador). La iniciativa es un reflejo de la necesidad del promotor/investigador por lograr que sus colegas reconocieran ciertas prácticas docentes en torno al trabajo matemático que parecían ser efectivas para promover el aprendizaje geométrico.
La dinámica en las reuniones fue la siguiente: a) presentación de la actividad por el promotor/investigador; b) interacción con los materiales; c) reflexión/discusión de las respuestas a las preguntas planteadas en los materiales. En el momento de la presentación, el promotor/investigador explicaba a sus colegas en qué consistía la actividad, cuál era su objetivo y qué tareas debían ser resueltas.
Luego de esto, los profesores se dedicaban a interactuar con los materiales de la actividad y tomar nota de aquellos aspectos que les permitieran formular respuestas. Finalmente, en el momento de la reflexión/discusión, los profesores intervenían de manera organizada para comunicar sus respuestas a las preguntas de la discusión, generándose un debate sobre tales respuestas.
En ocasiones, las ideas más relevantes de la discusión fueron anotadas en la pizarra para luego ser usadas en la redacción de un documento o cualquier otro material que resumiera lo tratado en la reunión o que pudiera servir para otros promotores.
5.2 Materiales de la actividad e información analizada
Para centrar la atención de los profesores en el proceso de trabajo matemático, el promotor/investigador preparó cinco materiales en formato de vídeo. Cada material plantea la tarea de analizar un registro de la práctica de trabajo matemático de un club GeoGebra, partiendo de unas preguntas generadoras (Figura 6). El uso de vídeos en las reuniones se apoya en la idea de que estos recursos tienen la capacidad de motivar la reflexión de los profesores en cuanto a las prácticas de resolución de las tareas de construcción. Al respecto, Hollingsworth y Clarke (2017)HOLLINGSWORTH, H.; CLARKE, D. Video as a tool for focusing teacher self-reflection: supporting and provoking teacher learning. Journal of Mathematics Teacher Education, Dordrecht (Holanda), v. 20, n. 5, p. 457-475, 2017. afirman que el uso de videos en la educación del profesor de matemática ayuda a que estos individuos reconozcan aquello que permanece oculto en las prácticas del aula.
En el material 1, usado en la primera reunión, se pide a los profesores que describan el modo en que los alumnos y el promotor trabajan en una estrategia para superar la inconsistencia geométrica de la construcción realizada por uno de los jóvenes. El vídeo muestra al promotor/investigador gestionando una discusión en gran grupo que versó en la construcción de un trapecio circular que presenta inconsistencia (Figura 7, ilustración a), centrando la atención tanto en el error como en la forma de superarlo. En este caso, el error es puesto de manifiesto por el promotor al arrastrar la construcción por uno de sus puntos libres (punto D en la Figura 7, ilustración a), produciendo una variación en la longitud del arco h que no debería darse.
Los materiales 2 y 3 fueron usados en la segunda reunión. El material 2 presenta un fragmento de una sesión de trabajo del club en el cual se observa al promotor/investigador discutiendo con los alumnos sobre la posible consistencia de la construcción del mismo trapecio circular del material 1, esta vez realizada por otro de los alumnos. A partir de la práctica registrada en el vídeo, los profesores debían describir las formas de actuar del promotor con sus alumnos al momento de la discusión, tomando en cuenta las conclusiones derivadas de la sesión anterior.
El material 3 pedía a los profesores reconocer la inconsistencia geométrica en la construcción de un óvalo e identificar las posibles causas de esta inconsistencia. En el vídeo se observa a dos alumnos explicando al promotor/investigador la manera cómo han resuelto la tarea de simulación de la cual deriva la construcción del óvalo.
Los materiales 4 y 5 se utilizaron durante la tercera reunión. El material 4 plantea la tarea de identificar aspectos relevantes de la práctica de analizar construcciones en 3D, a partir de las explicaciones que dan los alumnos de las técnicas empleadas. El vídeo gira en torno a una conversación entre el promotor/investigador y un alumno, en donde el primero intenta persuadir al segundo de la inconsistencia en la construcción de dos cilindros rectos, que el joven realizara previamente con su compañero de equipo en una sesión anterior.
Finalmente, el material 5 fue creado para que los promotores identificaran características de la manera de matematizar y trabajar matemáticamente en base a figuras 3D. Para ello, el vídeo muestra al promotor/investigador guiando estos procesos con el mismo alumno del material 4, en un momento inmediatamente posterior a la detección de la inconsistencia. Las figuras tratadas en el vídeo son un cilindro recto (el segundo de los dos referidos en el material 4) y un prisma cuadrangular.
Las discusiones de los profesores con respecto a los materiales fueron registradas en vídeo. Además, antes y después de la primera reunión, se produjeron documentos escritos que presentan, por un lado, las reflexiones del promotor/investigador sobre los resultados de las primeras sesiones de trabajo con sus alumnos (fuente de motivación de las reuniones) y, por otro lado, un resumen de los aspectos más importantes de lo discutido en ese momento. La información analizada en esta investigación proviene del contenido de los vídeos de las tres reuniones y de los planteamientos en los documentos escritos.
5.3 Análisis de la información
El análisis de la información se realizó mediante un proceso de selección, trascripción e interpretación, que ha permitido dar cuenta de los saberes relacionados con la manera en que los promotores gestionan el trabajo matemático de los alumnos. En el momento de la selección, realizamos un primer análisis de los vídeos de las reuniones, con el fin de identificar y seleccionar los segmentos destacados (RADFORD, 2015RADFORD, L. Methodological aspects of the theory of objectification. Revista Perspectivas da Educação Matemática, São Paulo, v. 8, n. 18, p. 547-567, 2015.).
Cada uno de estos segmentos reproduce un fragmento de vídeo con evidencias del reconocimiento por los promotores de algún saber relacionado con la gestión del trabajo matemático. Para la selección de los segmentos, se tuvo en cuenta que éstos reflejaran el pensamiento de los profesores sobre alguna posible secuencia de acciones (o alguna acción en particular) que pudiera favorecer la resolución conjunta de las tareas de construcción tratadas en los materiales.
En el momento de la organización, los segmentos destacados fueron trascritos en cuadros de tres columnas (Cuadro 1), utilizando un procesador de texto. La primera columna aporta información sobre el número de línea asignado a cada intervención de los profesores en el segmento. En la segunda columna aparece el contenido de la trascripción para cada una de las líneas que componen al segmento. La tercera columna estaba reservada para el próximo momento del análisis.
El momento de la interpretación se desarrolló en dos pasos. En el primer paso, las trascripciones fueron interpretadas desde los referentes teóricos que sustentan la investigación, permitiendo asignar a cada segmento (o una parte de éste) alguna categoría conceptual de análisis que reflejara determinado aspecto constitutivo de un saber codificado por los profesores (p. ej., problemáticas, propósitos, acciones concretas, entre otros aspectos) que le otorgara sentido. Podríamos decir que este paso se caracteriza por el reconocimiento de temáticas significativas, en el sentido de Freire (2002)FREIRE, P. Concientización: teoría y práctica de una educación liberadora. Buenos Aires: Galerna, 2002. en su método de concientización, a través de las cuales es posible desmitificar la realidad.
En el segundo paso, las categorías de análisis fueron organizadas para dar lugar a un discurso que permitiera describir cada saber asociado con la gestión del trabajo matemático. Esto sirvió para tomar decisiones en cuanto a la manera de presentar los resultados.
6 Resultados
El análisis de la información permitió identificar dieciocho segmentos destacados que presentan evidencias de los saberes necesarios para gestionar el trabajo matemático durante la elaboración de simuladores con GeoGebra. En estos segmentos, las reflexiones de los profesores sobre las prácticas reflejadas en los materiales han puesto de manifiesto ciertas maneras de pensar y actuar del promotor y los alumnos en distintos momentos del trabajo matemático. Específicamente, se han identificado tres potencialidades relacionadas con la resolución de las tareas de construcción que surgen al trabajar matemáticamente.
Un primer saber (S1) se puso de manifiesto en doce segmentos con reflexiones de los profesores sobre la manera de enfrentar la inconsistencia en construcciones realizadas a partir de técnicas erradas. El segundo saber (S2) se manifestó en cuatro segmentos destacados, en donde los profesores discutieron sobre las prácticas de comunicación de las técnicas empleadas para resolver eficientemente una determinada tarea de construcción. Finalmente, un tercer saber (S3) se reveló en dos segmentos destacados que presentan reflexiones sobre cómo formular técnicas de construcción que produzcan dibujos consistentes, antes de que éstas sean empleadas por los alumnos (Figura 8).
En lo que sigue, se describen los principales aspectos característicos de cada uno de estos saberes.
6.1 Saber cómo analizar la inconsistencia de una construcción geométrica (S1)
El análisis de la inconsistencia de una construcción (S1) se puso de manifiesto en las reuniones cuando los profesores reflexionaron sobre las prácticas del promotor y sus alumnos en los materiales 1, 2 y 4. Estas prácticas fueron guiadas por el deseo de superar la inconsistencia en dibujos producidos por medio de técnicas erradas. En un principio, la necesidad de que los alumnos adquirieran este saber fue revelada en las reflexiones subjetivas del promotor/investigador antes de la primera reunión, como consta en el primer documento escrito.
En cuanto al contenido de las reflexiones de los profesores sobre S1, fue posible identificar lo siguiente: (1) la importancia de saber analizar la inconsistencia en construcciones producidas con técnicas erradas; (2) el propósito detrás de este saber; y (3) la secuencia de acciones y reflexiones (etapas) que guían dicho análisis.
Con relación al primer contenido, los profesores consideraron importante que los alumnos aprendieran a analizar construcciones inconsistentes, ya que resolver una tarea de construcción implica obtener un dibujo dinámico con consistencia geométrica, y porque tal producción suele resultar difícil de lograr, especialmente en las primeras experiencias de los alumnos con el software. En la siguiente línea, se presenta evidencia de este tipo de reflexiones, producida por uno de los profesores durante la primera reunión:
60. Rafael: En relación a por qué es importante discutir esto [refiriéndose a S1] con los alumnos, yo encontré dos. Primero, la más importante, es que elaborar un simulador supone construir un dibujo dinámico que tenga consistencia. […] Por eso es importante hacer la prueba del arrastre y discutir con ellos por qué debemos hacerlo. Y segundo, más o menos lo que decía Ivonne, la construcción de un dibujo dinámico supone trabajar matemáticamente. Eso debemos decírselo a los alumnos: “Para que ustedes construyan un dibujo dinámico, deben usar matemática”. Ahora, eso implica que, cuando yo hago un dibujo dinámico, yo tenga que someter eso a la prueba del arrastre para ver en qué medida las acciones y decisiones que yo tomé al momento de construir se basaron en teoría […] (Habla del profesor Rafael, 2017).
Con respecto al segundo contenido, el análisis de la información permitió identificar el propósito que guio al promotor en su empeño por hacer que los alumnos aprendieran a analizar la inconsistencia de construcciones elaboradas con técnicas erradas. En concreto, el interés del promotor por lograr que uno de sus alumnos se involucre activamente en las prácticas sociales producidas en el interior del trabajo matemático, fue lo que motivó al promotor/investigador a realizar esfuerzos en la dirección de S1, como consta en la línea 97:
97. Promotor/Investigador: […] ¿Cuál fue mi estrategia con Liomar? [alumno del material 2]. Liomar es un joven que está en el club, pero se ha mantenido allí de forma periférica. ¿Qué quiere decir que ha estado de forma periférica? Que él no ha tenido el mismo protagonismo que otros alumnos del club. ¿Por qué? Porque esos otros alumnos “vuelan” [son muy hábiles]. Más bien, Liomar ha estado viendo los toros desde la barrera. Entonces, ¿cuál es mi preocupación? Lograr hacer que este alumno se involucre, se integre completamente al club y que se sienta como un participante que también puede dar buenas ideas y producir buenos materiales. […] Los alumnos deben sentir que están produciendo en el club y quizás nosotros nunca nos hemos puesto a pensar en eso (Habla del Promotor/Investigador, 2017).
En cuanto al tercer contenido, se encontraron evidencias del reconocimiento de una manera particular de analizar la inconsistencia de dibujos elaborados con técnicas erradas, tanto en las reflexiones sobre los materiales 1 y 2, como en el documento escrito luego de la primera reunión. Esta forma de análisis estaba compuesta por tres etapas. La primera etapa de S1 consiste en aplicar la prueba del arrastre con el propósito de que los alumnos logren identificar la inconsistencia de la construcción, esto es, aquella cualidad del objeto geométrico que pierde sus propiedades cuando el dibujo correspondiente es arrastrado por alguno de sus elementos libres, tal como se presenta en el caso del material 1:
2. Promotor/Investigador: Una cosa importante aquí. ¿Cuál fue la inconsistencia que yo identifiqué? La de la medida del arco, porque la longitud del arco no podía variar. Incluso, arrastré y les mostré [a los alumnos] que, si esta longitud estaba variando, entonces eso no podía pasar.
3. Ivonne: Yo consideré importante que tú [dirigiéndose al Promotor/Investigador] hicieras ver a los alumnos que la construcción tenía una inconsistencia, y no decirles de una vez [que] “todo eso está malo”. Sino más bien que ellos mismos, a través de la prueba del arrastre, se dieran cuenta de que su construcción no estaba bien. No es lo mismo cuando ellos se dan cuenta de una inconsistencia a través de lo que están observando y manipulando.
4. Luis: La acción del promotor fue hacerlos consientes de la cuestión que está allí [la inconsistencia].
5. Ivonne: Exactamente.
6. Stephanie: Y todo eso se hace a través de la prueba del arrastre (Diálogo entre el Promotor/Investigador y los profesores, 2017).
En el mismo segmento se pudo notar que, para algunos profesores, identificar inconsistencias es una habilidad del promotor que debe ser adquirida por los alumnos de los clubes y que puede conducir al refinamiento de la técnica empleada en la construcción, como queda evidenciado a continuación:
10. Rafael: […] En este momento, el protagonismo se lo lleva la prueba del arrastre. Pero la prueba del arrastre está influenciada por una información que el promotor ya sabe de antemano. El promotor identificó una cuestión en la construcción del muchacho [alumno]. Entonces, el promotor actuó a sabiendas de que la prueba del arrastre tenía esa finalidad, porque él identificó algo previamente.
11. Promotor/Investigador: […] ¿Por qué escogí el archivo de Carlos [alumno del material 1]? Porque ya le había hecho una revisión, esta era la segunda, y yo pensaba que el chamo [alumno] había trascendido su problema. Y resulta que el problema persistía.
12. Rafael: Lo que yo considero importante aquí es que el promotor tenga la habilidad de identificar esas cuestiones cuando procede a refinar [la técnica], porque si no, se le escapa la situación y no termina de sacar provecho.
13. Stephanie: Una ventaja de los promotores es que, cuando miramos los puntos de la construcción, los colores que tengan estos puntos nos ayudan a ver que hay una inconsistencia […].
14. Luis: Bueno, esa misma percepción de algo inconsistente debemos desarrollarla también en los chamos [alumnos] (Diálogo entre el Promotor/Investigador y los profesores, 2017).
La segunda etapa de S1 consiste en reconocer el error. En esta etapa, el promotor y los alumnos se dedican a revisar cada paso de la técnica empleada con el fin de reconocer la acción errónea que origina la inconsistencia, como lo comentan dos profesores en las siguientes líneas:
17. Stephanie: En ese análisis, ustedes [refiriéndose a los individuos del material 1] observan los elementos utilizados para la construcción con el propósito de identificar en dónde está el error. Porque había una parte de la construcción que era válida, pero no en donde el punto celeste se movía para aumentar la longitud del arco.
18. Luis: Es decir, ellos querían saber en qué punto de la técnica se cometió el error.
19. Stephanie: Si, en qué parte del protocolo de construcción está el error, para borrar eso y proceder a la reconstrucción de la representación.
20. Luis: Es que tú [dirigiéndose al Promotor/Investigador] lo dijiste muy bien en el vídeo: “el problema estuvo aquí, cuando [el alumno del material] construyó la recta”. Y borraste desde aquí [refiriéndose a una de las rectas], y no desde aquí [refiriéndose a la otra recta (Diálogo entre el Promotor/Investigador y los profesores, 2017).
Un aspecto que destacar de esta etapa tiene que ver con el papel que desempeña la teoría geométrica en el descubrimiento del error. Para los profesores, lo que un individuo sabe del objeto geométrico que intenta representar (características, propiedades, relaciones) con el GeoGebra, tiene implicaciones en aquello que es visto como fuente del error. Por ejemplo, en las siguientes líneas, algunos profesores asocian el error en la construcción del trapecio circular del material 1 con la variación en la medida, ya sea del arco del contorno de la figura, o del ángulo central correspondiente a este arco (saberes geométricos), lo que se pone de manifiesto tras el arrastre del dibujo por sus elementos libres:
28. Stephanie: Tú [dirigiéndose al Promotor/Investigador] utilizaste la relación entre rectas para hacer la construcción. En cambio, yo mantuve la longitud del arco (arco h en laFigura 7a). Yo les dije que la longitud del arco debía ser fija, no podía variar.
29. Promotor/Investigador: Pero entonces usaste otra herramienta.
30. Stephanie: Utilicé otra herramienta.
31. Promotor/Investigador: Ya estamos hablando de la teoría. La teoría, en mi caso, fue la posición relativa entre rectas.
32. Stephanie: En mi caso, fue la longitud del arco.
33. Rafael: Yo creo que eso va un poco más allá. Cuando vi el vídeo yo me pregunté si sería eso, o sería más bien la relación que existe entre la longitud del arco y el ángulo central. Porque esa relación es directa. Si crece el ángulo, crece el arco, y viceversa.
34. Promotor/Investigador: Yo no pensé en eso. Yo pensé en la relación de posición entre rectas que, ustedes saben muy bien, el ángulo es lo que determina todo. Si el ángulo es de 90 [grados], las rectas tienen una posición particular (Diálogo entre el Promotor/Investigador y los profesores, 2017).
Durante la tercera reunión, el reconocimiento del error sobre la base de la teoría geométrica fue considerado como una manera de detectar inconsistencias y una oportunidad para adquirir esos saberes geométricos necesarios para representar la figura que se tenga con el software. En este sentido, la siguiente línea muestra cómo una de las profesoras reconoce que la caracterización del cilindro (teoría geométrica), puesta de manifiesto en el material 4, permitió que ella y sus colegas detectaran el error en la construcción de esta figura:
174. Stephanie: Yo quería decir algo. Cuando hacemos este tipo de análisis de la inconsistencia, lo teórico lo llevamos como de forma muy superficial. En cambio, aquí, tú [dirigiéndose al Promotor/Investigador] haces un análisis profundo de todos los elementos que el alumno necesita para construir el cilindro. Eso es algo importante que pudiéramos hacer, porque con eso podríamos detectar una inconsistencia. Si tú no hablas con él sobre las alturas, los radios y todo eso, nosotros no podemos ver que no hay relación entre las alturas y los radios de ambos cilindros. ¿Qué pasa? Pasa que como tú haces un análisis previo de la altura del cilindro, dices qué radio es mayor que el otro, eso nos ayudó a reconocer algo que tú no habías visto. Ese es el valor que yo le doy a la parte teórica del objeto. Y que hace que el muchacho [alumno] comience a llamar al cilindro por su nombre. Haces un énfasis que, en mi caso, yo no hago. […] Y así es que se tiene que manejar (Habla de la profesora Stephanie, 2017).
La tercera etapa de S1 consiste en modificar la construcción. A sabiendas del error cometido, en esta etapa, los alumnos modifican la técnica de construcción con el fin de obtener un dibujo con consistencia geométrica, lo que les permite avanzar en la actividad. En el siguiente fragmento, extraído del documento escrito luego de la primera reunión, la modificación de la construcción es considerada como el producto de un refinamiento de la técnica empleada por los alumnos:
El tercer paso fue modificar la construcción. Este paso se hace con el propósito de solventar el error para obtener una construcción consistente, fundamentada en teoría geométrica. La modificación de la construcción supone un “trabajo matemático” de refinamiento de la técnica de construcción de los estudiantes (Documento de la primera reunión, 2017).
6.2 Saber cómo comunicar una técnica de construcción (S2)
El asunto de la comunicación de una técnica de construcción (S2) se puso de manifiesto en la segunda reunión, cuando los profesores discutían sobre las prácticas del promotor y sus alumnos en el material 3. En sus primeras reflexiones, los profesores asociaron la comunicación de técnicas de construcción con la necesidad de hacer que los alumnos fueran capaces de explicar a otros las técnicas empleadas para resolver determinada tarea de construcción. Más adelante, en el transcurso de la discusión, los profesores también reconocieron que la adquisición de este saber podía favorecer el desempeño de los alumnos en el momento de la sistematización de las experiencias de construcción. Las siguientes líneas corresponden a dos segmentos distintos, los cuales presentan evidencias de lo anterior:
100. Ivonne: Exactamente, a eso me refiero. Por supuesto, si ese alumno fue el que más participó, [entonces] es el que tiene más herramientas para explicar cómo hizo la construcción. Sin embargo, pude notar que se le hace complicado decir cada paso de la construcción y, por eso, tú [dirigiéndose al Promotor/Investigador] debías estar dirigiendo la cosa: “Ajá, pero ya va, con calma. Vamos otra vez, qué hiciste”. Porque él iba rapidísimo, y se saltaba pasos.
127. Promotor/Investigador: […] Parece que estamos en presencia de otro nuevo tópico. No solamente se trata del análisis de la inconsistencia, sino que también debemos centrar la atención en la comunicación de las ideas. En este caso, la comunicación de las técnicas de construcción, y cómo se puede comunicar mejor mi técnica, cómo yo la puedo comunicar a la gente. Eso es algo que nosotros podemos debatir también con los alumnos. […] Entonces, vuelvo e insisto, ¿será un tópico nuevo que tratar con los muchachos [alumnos]? Necesitamos esas prácticas entonces. Y fíjense que las prácticas sobre la comunicación no pueden hacerse sobre técnicas inconsistentes, sino sobre técnicas consistentes (Diálogo entre el Promotor/Investigador y los profesores, 2017).
Aunque, en el caso del material 3, la comunicación ocurre luego de la aplicación de una técnica errada, al final de la línea 127 se puede ver que el promotor/investigador encuentra sentido para S2 en relación con las técnicas que producen dibujos geométricamente consistentes, lo que ubica al proceso de comunicación de una técnica al final del trabajo matemático. En otras intervenciones, los profesores reconocen que la comunicación de una técnica de construcción es una práctica guiada por las preguntas del promotor, que requiere de una actitud responsable de parte de los alumnos, como se puede ver en la siguiente línea:
105. Madeleisy: A mí me gustó ver que tú [dirigiéndose al Promotor/Investigador] le preguntaras al alumno qué fue lo que hizo y cómo lo hizo, porque él se iba dando cuenta, o sea, iba recordando su construcción y ahí podíamos notar verdaderamente si aprendió de lo que había hecho y si lo podía compartir con sus compañeros. Y que, aparte de toda la matemática que hay allí [en la aplicación de una técnica], los alumnos también van a notar que es importante escribir y quizás, desde el inicio, ellos se van adaptando más y no se les hace tan difícil ir escribiendo sus experiencias. […] Y me pareció muy bueno, o sea, me gustó mucho el hecho de preguntar, que es algo bastante importante hacer, preguntarle al estudiante qué fue lo que hizo, porque uno se da cuenta de todas esas cosas (Habla de la profesora Madeleisy, 2017).
Para los profesores, la función de las preguntas hechas por el promotor durante la comunicación de una técnica es la de dirigir la atención de los alumnos hacia aquellas propiedades y relaciones geométricas relevantes para la justificación de los pasos que la componen. Otro aspecto importante de la comunicación tiene que ver con la cultura material alrededor de las explicaciones de los alumnos. Con respecto a esto, los profesores reconocieron la necesidad de crear bocetos de los objetos geométricos construidos, para ser utilizados como soporte en el momento de la explicación de la técnica empleada, como se puede notar en la siguiente línea:
139. Stephanie: Yo valoro mucho el hecho de que el boceto ayude a los alumnos a comunicarse, y con esto le estamos viendo el sentido al uso del boceto, un sentido más práctico. Porque, a veces, los alumnos no lo ven, se preguntan: “¿para qué voy a hacer el boceto?”. Ellos se van de una vez a la conclusión. Fíjate que los alumnos del vídeo, para poder comunicarse, para poder hacer eso, necesitaron del boceto. Porque tú le hablabas y, ajá, no se entendía. Y luego, con el boceto, a ellos se les hizo más fácil darse a entender, no. De verdad que, a mí, esa parte, o sea, es un material muy bueno que me está dando mucha información para lo que vamos a hacer en enero (Habla de la profesora Stephanie, 2017).
6.3 Saber cómo anticipar una técnica de construcción (S3)
La necesidad de anticipar una técnica de construcción (S3) surge durante la tercera reunión, ante las críticas a las prácticas de resolución de tareas de construcción desarrolladas directamente sobre la interfaz del software. Al respecto, el promotor/investigador reconoce que la tendencia de los promotores a gestionar la producción de técnicas de construcción bajo la manipulación directa de las herramientas del software, en una suerte de ensayo y error, no permite que los alumnos reflexionen, produzcan y validen sus propios procesos de construcción, como queda revelado a continuación:
210. Promotor/Investigador: Si se hace. Pero, de pronto, como dice Rafael, los promotores vamos directamente al software, y allí comenzamos a discutir con los alumnos: “Ajá, sí, quítala, ponla, que tal, no sé qué”. Pero no les permitimos que reflexionen, primero, sobre cómo usarían la herramienta tecnológica, antes de ir al software. Y no es igual. Porque cuando tú vas a la herramienta, ésta te puede cambiar las cosas. Tú puedes pensar en hacer algo al principio y, al final, terminas haciendo otra cosa. ¿Por qué? Porque si voy a construir una perpendicular, despliego el menú de herramientas[auxiliares], y veo la opción “Paralela”, sale otra cosa. Es decir, no es igual […] (Habla del Promotor/Investigador, 2017).
Según los profesores, S3 ayuda a que los alumnos logren establecer de antemano una técnica de construcción que luego puedan reproducir fácilmente en la vista gráfica del GeoGebra, sin mayores retardos ni equívocos, como se indica en la línea siguiente:
218. Promotor/Investigador: Entonces, estamos haciendo lo que debemos hacer, desde mi punto de vista. Porque lo que yo quiero es que mis alumnos sean capaces de, inclusive, antes de meterse en el software, anticipar un proceso de construcción. Que lo anticipen. O sea, que ellos sean capaces de mirar el modelo matemático y decir: “aquí va una recta y tal”. Y luego vayan allá [al software] y reproduzcan la técnica. Eso es lo que yo quiero desarrollar en mis estudiantes. Y si ellos logran desarrollar eso, mira, yo creo que mis alumnos, solos, independientes, van a lograr rápidamente resolver las tareas (Habla del Promotor/Investigador, 2017).
Para finalizar, en sus reflexiones, los profesores reconocen la importancia de apoyar la gestión del proceso de anticipación de una técnica en una figura de análisis sobre la cual se señalan las construcciones auxiliares necesarias para la representación del objeto geométrico en la interfaz del software. En la siguiente línea se presenta evidencia del reconocimiento de un profesor de esta clase de figuras en una experiencia de promoción pasada:
193. Rafael: Y, de hecho, estoy recordando que, en mi club del año pasado, Meganys [alumna del club mencionado], cuando estaba representando el seguidor (pieza del fenómeno que se trata de simular), vio un rectángulo y luego dibujó una figura de análisis en el pizarrón, y sobre ella vimos las perpendiculares, todos los elementos que luego reproducir allá, en el GeoGebra. Pero yo nunca me di cuenta de que era una figura de análisis. Nunca fui consciente. Ahora lo estoy siendo (Habla del profesor Rafael, 2017).
7 Discusión y conclusiones
En esta investigación hemos analizado las discusiones de siete profesores de matemática (todos promotores del Club GeoGebra) que se reunieron para examinar los modos en que un promotor y sus alumnos transitan por el proceso de trabajo matemático en diferentes momentos. La intención con el análisis era identificar y describir aquellos saberes necesarios para la gestión del trabajo matemático en los clubes GeoGebra, por lo tanto, nos interesamos por las potencialidades que, según el criterio de los profesores, emergieron de las prácticas de resolución de tareas de construcción con GeoGebra, discutidas por los profesores. Los resultados del estudio dan cuenta de tres saberes vinculados a la gestión del trabajo matemático, que fueron movilizados por el promotor antes, durante y después de la resolución de las tareas de construcción mostrada en los vídeos.
Los resultados del estudio indican que estos saberes fueron movilizados en atención a una necesidad ética de la profesión docente manifestada en los promotores: lograr que los alumnos aprendan geometría mientras resuelven las tareas de construcción, comunicar a otros las técnicas empleadas para resolver las tareas o anticipar una técnica para garantizar un mejor desempeño a futuro. Este hallazgo confirma que los saberes de la gestión del trabajo matemático se encuentran fuertemente enraizados en las experiencias concretas de los promotores. Sin embargo, la perspectiva teórica asumida en esta investigación nos permite entender que el reconocimiento de estos saberes no solo tiene su lado subjetivo, sino también un lado cultural que vale la pena discutir en los siguientes apartados.
7.1 La experiencia de enseñanza de los promotores como fuente de los saberes
Como mencionamos al inicio del este trabajo, los saberes movilizados por los profesores durante la elaboración de simuladores con GeoGebra tienen una naturaleza práctica, ya que forman parte de la propia experiencia de enseñanza. Por esta razón, y tomando con base las evidencias arrojadas por el estudio, consideramos que la experiencia de los promotores en los clubes, y su conocimiento del trabajo matemático que allí se realiza, han tenido influencia en el reconocimiento de los saberes necesarios para gestionar la manera en que los alumnos analizan construcciones inconsistentes (S1), comunican a otros sus técnicas de construcción (S2) y anticipan estas técnicas (S3).
Este hecho revela la importancia relativa que adquiere la experiencia práctica de los promotores en esta investigación, sobre todo si se piensa que la práctica docente proporciona los principios básicos para enfrentar y solucionar las situaciones concretas que obstaculizan el desempeño de los alumnos durante las actividades del aula (TARDIF, 2002TARDIF, M. Los saberes del docente y su desarrollo profesional. Madrid: Narcea, 2002.).
En el caso de S1, las prácticas de construcción geométrica reflejadas en los materiales 1, 2 y 4, aportaron la información necesaria para que los profesores establecieran una secuencia de acciones, comprendida por tres etapas (aplicar la prueba del arrastre, reconocer el error y modificar la construcción), que sirve para dar respuesta al problema de la inconsistencia en construcciones realizadas por medio de técnicas erradas.
No obstante, llama la atención que los profesores no hicieran mención explícita de estas formas idealizadas de actuar para los casos de S2 y S3. Al mismo tiempo, resalta el hecho de que los profesores no discutieran sobre el papel del GeoGebra en la producción de significados durante la anticipación de una técnica, ni profundizaran en los problemas prácticos que los llevan a pensar que las técnicas de construcción deben ser ideadas en un entorno de lápiz y papel, antes de que ser empleadas con el software. La manera en que esta forma de gestión es discutida nos lleva a pensar que los profesores validan modos de actuar del promotor en S3 que limitan las potencialidades de experimentación con el GeoGebra reportadas por otros investigadores (VILLAREAL; BORBA, 2010VILLARREAL, M.; BORBA, M. Collectives of humans-with-media in mathematics education: notebooks, blackboards, calculators, computers and … notebooks throughout 100 years of ICMI. ZDM The International Journal of Mathematics Education, Berlin, v. 42, n. 1-2, p. 49-62, 2010.).
Posiblemente, una razón sea la poca familiaridad de estos individuos con las prácticas de comunicación y anticipación de técnicas de construcción, que se vieron reflejadas en los materiales 3 y 5. Es por esto que se sugiere al proyecto Club GeoGebra: (i) promover este tipo de prácticas entre sus promotores y (ii) abrir espacios para que ellos puedan reflexionar y fijar posición crítica ante estas experiencias, considerando diferentes casos. La atención a estas cuestiones puede crear condiciones favorables para el emprendimiento de otras investigaciones que ayuden a identificar y describir estos dos saberes con más detalle.
7.2 La transformación de la experiencia en saberes docentes
La experiencia de enseñanza de los promotores ha sido fundamental para el reconocimiento de los saberes reportados en este estudio. Sin embargo, a la luz de los resultados y tal como nos sugiere Radford (2017b)RADFORD, L. Aprendizaje desde la perspectiva de la Teoría de la Objetivación. En: D'AMORE, B.; RADFORD, L. Enseñanza y aprendizaje de las matemáticas: problemas semióticos, epistemológicos y prácticos. Bogotá: Universidad Distrital Francisco José de Caldas, 2017b. p. 115-136., la transformación de esta experiencia en potencialidades útiles para la gestión docente del trabajo matemático ha sido el resultado de una objetivación del saber, en donde interaccionan dos cuestiones relevantes de este proceso.
Por un lado, las formas ideales de reflexión y acción encarnadas en las prácticas discutidas por los profesores fueron reconocidas, no solo con base en la experiencia de los promotores, sino además en atención a determinados contenidos y valores propios de una cultura de trabajo matemático que es mediada por el uso de artefactos de naturaleza tecnológica. Para dar una idea, al considerar la prueba del arrastre como una de las etapas que comprende el análisis de construcciones inconsistentes (S1), los profesores interpretaron y validaron una de las modalidades de arrastre típica del trabajo en ambientes de geometría dinámica, la cual ha sido reportada por algunos investigadores, como Arzarello et al. (2002)ARZARELLO, F.; OLIVERO, F.; PAOLA, D.; ROBUTTI, O. A cognitive analysis of dragging practices in Cabri environments. ZDM The International Journal of Mathematics Education, Berlin, v. 34, n. 3, p. 66-72, 2002., ya hace algún tiempo.
Por otro lado, la conciencia colectiva de los profesores entra en contacto con elementos de esa cultura mediada por tecnologías digitales, que están allí antes de la transformación de la propia conciencia (RADFORD, 2017cRADFORD, L. Ser, subjetividad y alienación. En: D'AMORE, B.; RADFORD, L. Enseñanza y aprendizaje de las matemáticas: problemas semióticos, epistemológicos y prácticos. Bogotá: Universidad Distrital Francisco José de Caldas, 2017c. p. 137-165.). Podríamos decir que el reconocimiento de los saberes reportados aquí es una manifestación del encuentro de la conciencia de los profesores con un mundo de trabajo geométrico caracterizado por el trabajo con el ambiente dinámico que ofrece el GeoGebra.
7.3 Las reuniones de promotores como mediadoras de los saberes
Para finalizar, es importante destacar algunos aspectos relacionados con el carácter mediador que han tenido las reuniones analizadas en esta investigación. Si consideramos que cada reunión “ejerce su mediación por medio de artefactos, formas de uso de artefactos y también por medio de modos de interacción humana, que son históricos y culturales” (RADFORD, 2017aRADFORD, L. Saber y conocimiento desde la perspectiva de la Teoría de la Objetivación. En: D'AMORE, B.; RADFORD, L. Enseñanza y aprendizaje de las matemáticas: problemas semióticos, epistemológicos y prácticos. Bogotá: Universidad Distrital Francisco José de Caldas, 2017a. p. 97-114., p. 109), entonces, un primer aspecto a resaltar tiene que ver con los materiales incorporados a las reuniones.
Los resultados obtenidos indican que, en su conjunto, los materiales de vídeo usados en las reuniones cumplieron su función de motivar la reflexión de los profesores sobre el modo en que el promotor gestiona las prácticas de resolución de las tareas de construcción de sus alumnos. Sin embargo, las dificultades que tuvieron los profesores para profundizar en ciertas cuestiones de S2 y S3, tales como, el lugar de la teoría geométrica en la adquisición de estos saberes y la secuencia de acción y reflexión posible en cada caso, nos hacen pensar en que las preguntas de los materiales 3 y 5 no fueron tan asertivas como para provocar reflexiones focalizadas en estas cuestiones. Por ejemplo, a nuestro criterio, fue poco conveniente que la pregunta del material 3 estuviera dirigida hacia el error en la construcción del óvalo por parte de los alumnos, y no hacia el modo en que los jóvenes comunicaban al promotor la técnica de construcción empleada por ellos para dibujar esa figura con el software o hacia el modo en que el promotor actuaba para promover esa capacidad en el momento.
A pesar del obstáculo presente en el material 3, los profesores fueron capaces de reconocer a S2 como una potencialidad de su trabajo docente en los clubes, influenciados, quizás, por la manera en que habían discutido los materiales 1 y 2 (CLIMENT; CARRILLO, 2007CLIMENT, N.; CARRILLO, J. El uso de vídeos para el análisis de la práctica en entornos colaborativos. Investigación en la Escuela, Sevilla, n. 61, p. 23-35, 2007.) o por los modos de interacción humana que prevalecieron en estas discusiones (CALLEJO; VALLS; LLINARES, 2007CALLEJO, M.L.; VALLS, J.; LLINARES, S. Interacción y análisis de la enseñanza. Aspectos claves en la construcción del conocimiento profesional. Investigación en la Escuela, Sevilla, n. 61, p. 5-21, 2007.).
Aunque esto pueda ser así, nuestros resultados no aportan información para constatar estos hechos, razón por la cual vemos necesario que se realicen otras investigaciones que permitan develar la lógica de producción de los saberes docentes en las reuniones realizadas por los promotores. En cuanto a la teoría geométrica que interviene en la actividad, valdría la pena considerar iniciar estudios sobre los modos docentes de gestionar experiencias de trabajo matemático en los cuales los alumnos movilizan otro tipo de contenido matemático (por ejemplo, funciones, ecuaciones, intervalos, etcétera) para modelar las formas y movimientos característicos de los fenómenos evocados, como ocurre en el caso de Faria (2016)FARIA, R. Movimiento planetario en el sistema solar desde una perspectiva tridimensional. En: PRIETO, J. L.; GUTIÉRREZ, R. E. (Comp.). Memorias del II Encuentro de Clubes GeoGebra del Estado Zulia. Maracaibo: Aprender en Red, 2016. p. 85-98. con la ecuación de la elipse.
Reconocimientos
Este trabajo se ha realizado al amparo del proyecto de investigación No. CH-0510-15, adscrito al Centro de Estudios Matemáticos y Físicos (CEMAFI) y financiado por el Consejo de Desarrollo Científico, Humanístico y Tecnológico (CONDES) de la Universidad del Zulia, Venezuela.
-
1
Algunos ejemplos de simuladores computacionales se pueden consultar en: https://phet.colorado.edu/es/.
-
2
Los fenómenos seleccionados por alumnos de los clubes GeoGebra han sido reportados en Prieto y Gutiérrez (2015PRIETO, J. L.; GUTIÉRREZ, R. E. (Comps.). Memorias del I Encuentro de Clubes GeoGebra del Estado Zulia. Maracaibo: Aprender en Red, 2015., 2016PRIETO, J. L.; GUTIÉRREZ, R. E. (Comps.). Memorias del II Encuentro de Clubes GeoGebra del Estado Zulia. Maracaibo: Aprender en Red, 2016., 2017PRIETO, J. L.; GUTIÉRREZ, R. E. (Comps.). Memorias del III Encuentro de Clubes GeoGebra del Estado Zulia. Maracaibo: Aprender en Red, 2017.).
Referencias
- ARTIGUE, M. Aportes de la integración de tecnologías en la sala de clase de matemática, 2016. Disponible en: <https://www.youtube.com/watch?v=6v-DErde1GE&t=316s>. Acceso en: 12 oct. 2017.
» https://www.youtube.com/watch?v=6v-DErde1GE&t=316s - ARZARELLO, F.; OLIVERO, F.; PAOLA, D.; ROBUTTI, O. A cognitive analysis of dragging practices in Cabri environments. ZDM The International Journal of Mathematics Education, Berlin, v. 34, n. 3, p. 66-72, 2002.
- BOGDAN, R.; BIKLEN, S. K. Investigação qualitativa em educação: uma introdução à teoria e aos métodos. Portugal: Porto, 1994.
- CALLEJO, M.L.; VALLS, J.; LLINARES, S. Interacción y análisis de la enseñanza. Aspectos claves en la construcción del conocimiento profesional. Investigación en la Escuela, Sevilla, n. 61, p. 5-21, 2007.
- CLARK, D.; NELSON, B.; SENGUPTA, P.; D'ANGELO, C. Rethinking science learning through digital games and simulations: Genres, examples, and evidence. Washington DC: National Research Council, 2009.
- CLIMENT, N.; CARRILLO, J. El uso de vídeos para el análisis de la práctica en entornos colaborativos. Investigación en la Escuela, Sevilla, n. 61, p. 23-35, 2007.
- PONTE, J. P.; CHAPMAN, O. Mathematics teachers' knowledge and practices. En: GUTIÉRREZ, A.; BOERO, P. (Ed.). Handbook of Research on the Psychology of Mathematics Education: past, present and future. Rotterdam: Sense Publishers, 2006. p. 461-494.
- FARIA, R. Movimiento planetario en el sistema solar desde una perspectiva tridimensional. En: PRIETO, J. L.; GUTIÉRREZ, R. E. (Comp.). Memorias del II Encuentro de Clubes GeoGebra del Estado Zulia Maracaibo: Aprender en Red, 2016. p. 85-98.
- FIORENTINI, D; NACARATO, A.; PINTO, R. A. Saberes da experiência docente em matemática e educação continuada. Quadrante Revista Teórica e de Investigação, Lisboa, v. 8, n. 1-2, p. 33-60, 1999.
- FIORENTINI, D.; SOUZA, A.; MELO, G. A. Saberes docentes: um desafio para académicos e práticos. En: GERALDI, C. M. G.; FIORENTINI, D.; PEREIRA, E. M. (Org.). Cartografias do trabalho docente: professor (a)-pesquisador (a). Campinas: ALB e Mercado de Letras, 1998. p. 307-335.
- FREIRE, P. Concientización: teoría y práctica de una educación liberadora. Buenos Aires: Galerna, 2002.
- GONZÁLEZ-LÓPEZ, M. J. La Gestión de la Clase de Geometría utilizando Sistemas de Geometría Dinámica. En: GÓMEZ, P.; RICO, L. (Eds.). Iniciación a la investigación en Didáctica de la Matemática. Homenaje al profesor Mauricio Castro Granada: Universidad de Granada, 2001. p. 277-290.
- GONZÁLEZ, A. G.; MOLINA, J. G.; SÁNCHEZ, M. La matemática nunca deja de ser un juego: investigaciones sobre los efectos del uso de juegos en la enseñanza de las matemáticas. Educación Matemática, México D. F., v. 26, n. 3, p. 109-133, 2014.
- GREEFRATH, G. Using technologies: new possibilities of teaching and learning modelling– Overview. En: KAISER, G.; BLUM, W.; BORROMEO, R.; STILLMAN, G. (Eds.). Trends in the teaching and learning of mathematical modelling Dordrecht: Springer, 2011. p. 301–304.
- GUTIÉRREZ, R. Elaboración de simuladores con GeoGebra. Una actividad de modelación matemática mediada por tecnologías digitales. En: PRIETO, J. L.; GUTIÉRREZ, R. E. (Comp.). Memorias del III Encuentro de Clubes GeoGebra del Estado Zulia Maracaibo: Aprender en Red, 2017. p. 234-252.
- GUTIÉRREZ, R.; PRIETO, J. L.; ORTIZ, J. Matematización y trabajo matemático en la elaboración de simuladores con GeoGebra. Educación Matemática, México D. F., v. 29, n. 2, p. 37-68, 2017.
- HERSHKOWITZ, R. About reasoning in geometry. En: MAMMANA C.; VILLANI, V. (Ed.). Perspectives on the Teaching of Geometry for the 21th Century Dordrecht: Kluwer Academic Publishers, 1998. p. 29-83.
- HOLLINGSWORTH, H.; CLARKE, D. Video as a tool for focusing teacher self-reflection: supporting and provoking teacher learning. Journal of Mathematics Teacher Education, Dordrecht (Holanda), v. 20, n. 5, p. 457-475, 2017.
- LABORDE, C. Cabri Geómetra o una nueva relación con la geometría. En: PUIG L. (Ed.). Investigar y enseñar: variedades de la educación matemática. Madrid: Una Empresa Docente, 1997. p. 33-48.
- PELEY, S. La rotación en la simulación de un brazo robótico con el GeoGebra. En: PRIETO, J. L.; GUTIÉRREZ, R. E. (Comp.). Memorias del II Encuentro de Clubes GeoGebra del Estado Zulia Maracaibo: Aprender en Red, 2016. p. 249-257.
- PRIETO, J. L. Proyectos de simulación con GeoGebra: una estrategia del desarrollo del pensamiento científico desde el servicio comunitario. Trabajo de ascenso (Asociado) – Facultad de Humanidades y Educación, Universidad del Zulia, Maracaibo, 2017.
- PRIETO, J. L.; GUTIÉRREZ, R. E. (Comps.). Memorias del I Encuentro de Clubes GeoGebra del Estado Zulia Maracaibo: Aprender en Red, 2015.
- PRIETO, J. L.; GUTIÉRREZ, R. E. (Comps.). Memorias del II Encuentro de Clubes GeoGebra del Estado Zulia Maracaibo: Aprender en Red, 2016.
- PRIETO, J. L.; GUTIÉRREZ, R. E. (Comps.). Memorias del III Encuentro de Clubes GeoGebra del Estado Zulia Maracaibo: Aprender en Red, 2017.
- PUGNALONI, L. A. Los simuladores. El papel de la simulación en la ciencia. Ciencia Hoy, Buenos Aires, v. 105, n. 1, p. 27-34, 2008.
- RADFORD, L. Three key concepts of the theory of objectification: Knowledge, knowing, and learning. Journal of Research in Mathematics Education, Reston, v. 2, n. 1, p. 7-44, 2013a.
- RADFORD, L. Sumisión, alienación y (un poco de) esperanza: hacia una visión cultural, histórica, ética y política de la enseñanza de las matemáticas. En: RAMIREZ, A.; MORALES, Y. (Ed.). Memorias del I Congreso de Educación Matemática de América Central y El Caribe Santo Domingo: REDUMATE, 2013b.
- RADFORD, L. Methodological aspects of the theory of objectification. Revista Perspectivas da Educação Matemática, São Paulo, v. 8, n. 18, p. 547-567, 2015.
- RADFORD, L. Saber y conocimiento desde la perspectiva de la Teoría de la Objetivación. En: D'AMORE, B.; RADFORD, L. Enseñanza y aprendizaje de las matemáticas: problemas semióticos, epistemológicos y prácticos. Bogotá: Universidad Distrital Francisco José de Caldas, 2017a. p. 97-114.
- RADFORD, L. Aprendizaje desde la perspectiva de la Teoría de la Objetivación. En: D'AMORE, B.; RADFORD, L. Enseñanza y aprendizaje de las matemáticas: problemas semióticos, epistemológicos y prácticos. Bogotá: Universidad Distrital Francisco José de Caldas, 2017b. p. 115-136.
- RADFORD, L. Ser, subjetividad y alienación. En: D'AMORE, B.; RADFORD, L. Enseñanza y aprendizaje de las matemáticas: problemas semióticos, epistemológicos y prácticos. Bogotá: Universidad Distrital Francisco José de Caldas, 2017c. p. 137-165.
- RADFORD, L.; ROTH, W.-M. Intercorporeality and ethical commitment: An activity perspective on classroom interaction. Educational Studies in Mathematics, Dordrecht, v. 77, n. 2-3, p. 227-245, 2011.
- REIS, M. E. T.; AFFONSO, S. A. B. Os programas formais de formação continuada e sua relação com os saberes docente. Revista de Educação do Curso de Pedagogia do Campus Avançado de Jataí da Universidade Federal de Goiás, Jataí, v. 1, n.3, p. 1-18, 2007.
- RUBIO, L.; PRIETO, J. L.; ORTIZ, J. La matemática en la simulación con GeoGebra. Una experiencia con el movimiento en caída libre. International Journal of Educational Research and Innovation, Madrid, v. 2, n. 1, p. 90-111, 2016.
- SÁNCHEZ, I. Las prácticas matemáticas en la elaboración de simuladores con GeoGebra 2017. 113. Tesis (Maestría en Matemática Mención Docencia) – Posgrado de la Facultad de Humanidades y Educación, Universidad del Zulia, Maracaibo, 2017.
- SÁNCHEZ, I.; PRIETO, J. L. Características de las prácticas matemáticas en la elaboración de simuladores con GeoGebra. Números Revista de Didáctica de las Matemáticas, Tenerife, v. 96, p. 79-101, 2017.
- TARDIF, M. Los saberes del docente y su desarrollo profesional Madrid: Narcea, 2002.
- VILLARREAL, M.; BORBA, M. Collectives of humans-with-media in mathematics education: notebooks, blackboards, calculators, computers and … notebooks throughout 100 years of ICMI. ZDM The International Journal of Mathematics Education, Berlin, v. 42, n. 1-2, p. 49-62, 2010.
Fechas de Publicación
-
Publicación en esta colección
2 Dic 2019 -
Fecha del número
Sep-Dec 2019
Histórico
-
Recibido
07 Dic 2017 -
Acepto
23 Nov 2018


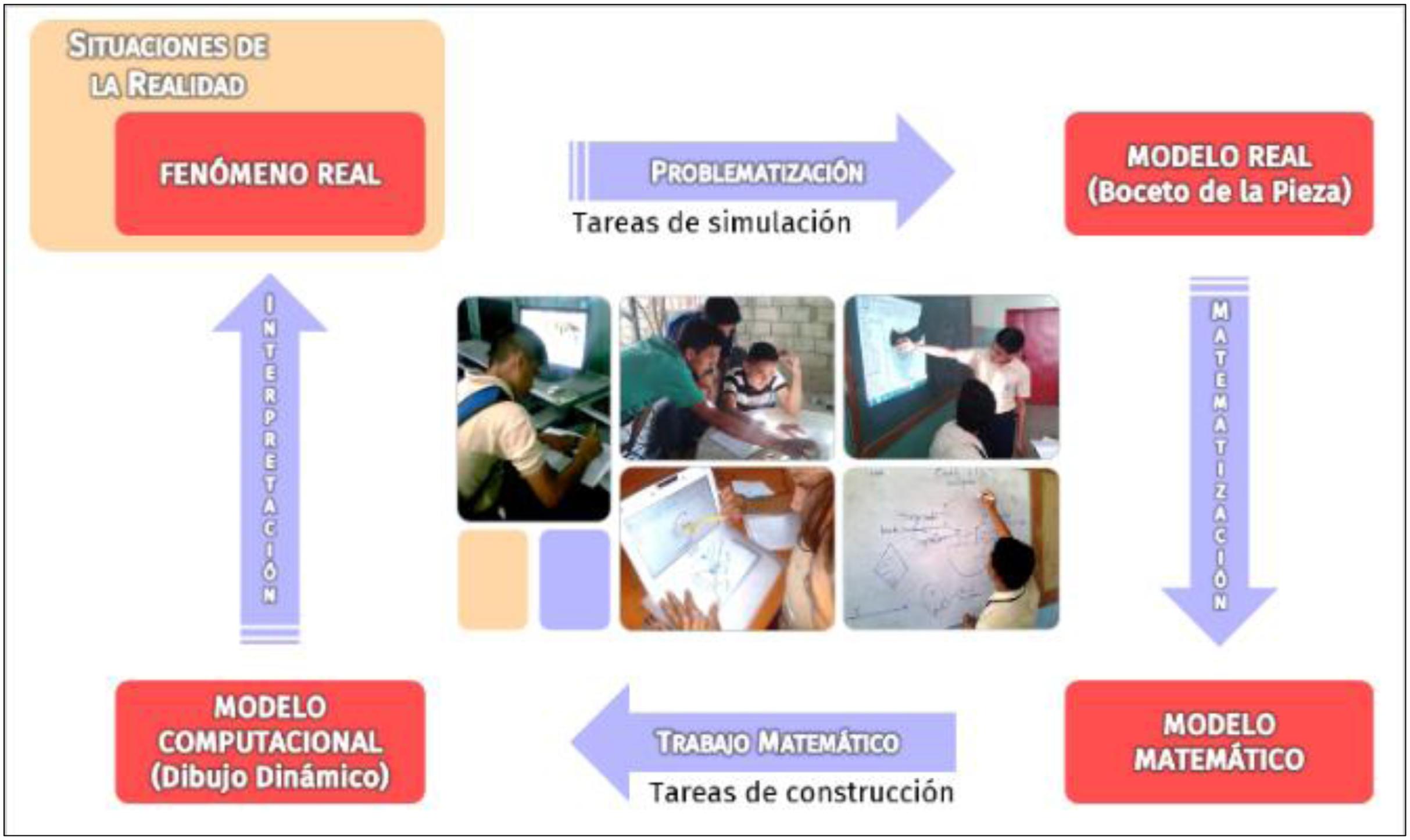 Fuente: autores
Fuente: autores
 Fuente: imágenes extraídas de
Fuente: imágenes extraídas de  Fuente: Información extraída de
Fuente: Información extraída de  Fuente: autores
Fuente: autores
 Fuente: información extraída de
Fuente: información extraída de  Fuente: imágenes extraídas del material, disponible en:
Fuente: imágenes extraídas del material, disponible en:  Fuente: autores
Fuente: autores
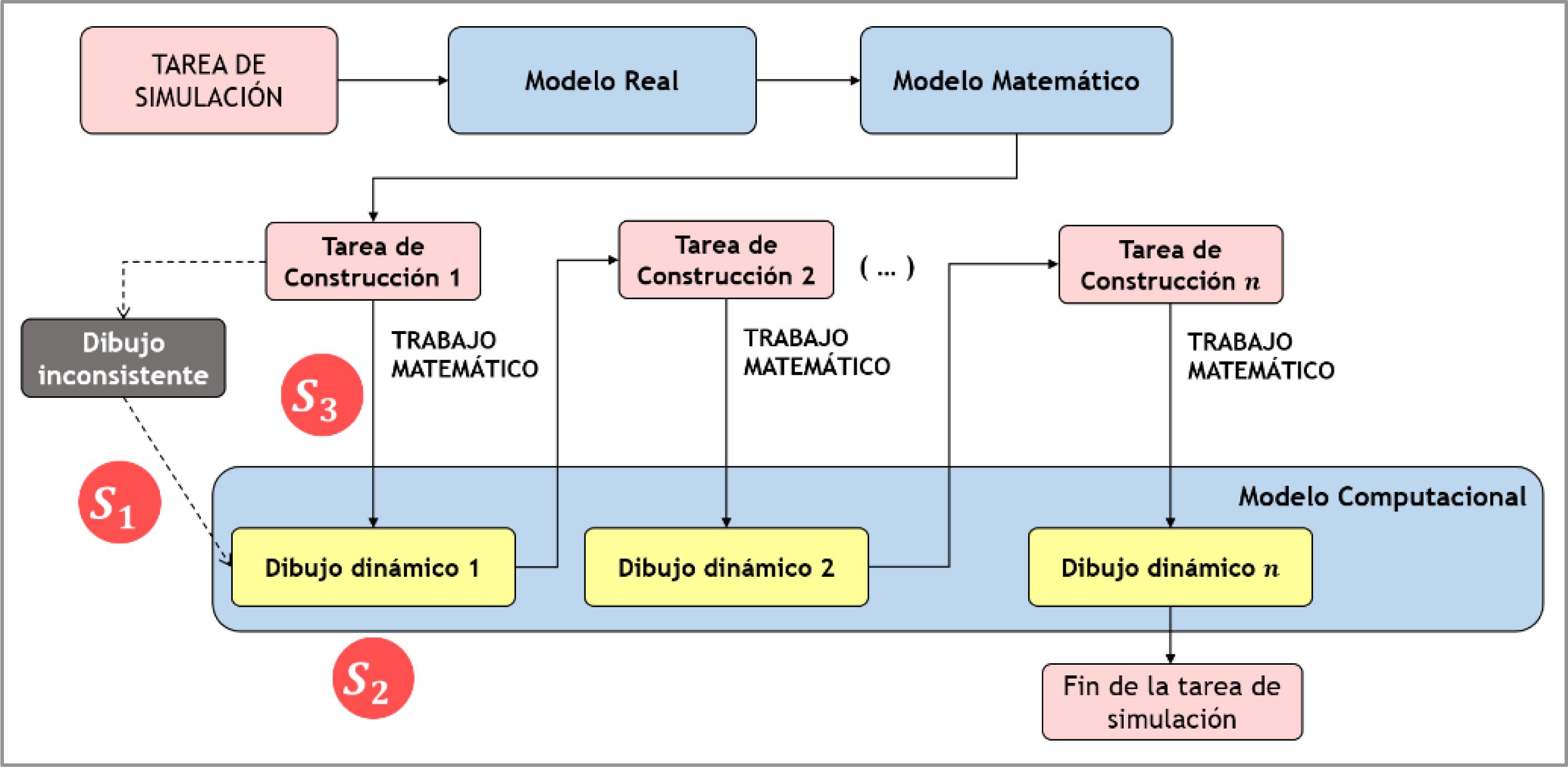 Fuente: autores
Fuente: autores