Estratégia de controle para o seguimento de referências em sistemas de tempo discreto com atuadores saturantes

Reference tracking strategy for discrete-time systems with saturating actuators

CONTROLE SOB RESTRIÇÕES

Estratégia de controle para o seguimento de referências em sistemas de tempo discreto com atuadores saturantes

Reference tracking strategy for discrete-time systems with saturating actuators

Jeferson Vieira Flores; João Manoel Gomes da Silva Jr

UFRGS - Departamento de Engenharia Elétrica, Av. Osvaldo Aranha 103, 90035-190 Porto Alegre-RS, Brasil, [e-mail], [e-mail]

RESUMO

Este trabalho aborda o problema de seguimento de referências em sistemas lineares sujeitos à saturação dos atuadores através de uma representação no espaço de estados. O objetivo é garantir o seguimento de referências constantes e a rejeição de perturbações também constantes, em regime permanente, através da adição de uma ação integral a uma malha de controle com realimentação unitária. Base-ado nesta estrutura, condições na forma de inequações matriciais são propostas para o projeto simultâneo de uma realimentação de estados estabilizante e de um controlador de anti-windup estático. Estas condições garantem que as trajetórias do sistema em malha fechada são limitadas em um conjunto invariante se as condições iniciais do sistema pertencerem a este conjunto e se as referências/perturbações pertencerem a um certo conjunto admissível. Problemas de otimização baseados em inequações matriciais lineares (LMIs) são então propostos para maximizar os conjuntos de referências/perturbações e/ou condições iniciais admissíveis.

Palavras-chave: seguimento de referências, saturação de atuadores, anti-windup, LMIs.

ABSTRACT

This paper addresses the problem of tracking constant references for linear systems subject to actuator saturation considering an state-space framework. The constant reference tracking and the constant disturbance rejection are taken into account by the introduction of an integral action in a unitary output feedback scheme. Based on this structure, conditions to design simultaneously a stabilizing feedback gain and an anti-windup gain are presented in the form of matrix inequalities. These conditions ensure that the trajectories of the closed-loop system are bounded in an invariant ellipsoidal set, provided that the initial conditions are taken in this set and the references and the disturbances belong to a certain admissible set. LMI-based optimization problems are then proposed to compute the gains aiming at enlarging the set of admissible references, disturbances or initial conditions.

Keywords: reference tracking, actuator saturation, anti-windup, LMIs.

1 INTRODUÇÃO

Nas malhas de controle reais, atuadores estão sujeitos a uma série de restrições, podendo estas serem tanto construtivas quanto inerentes ao processo que se deseja controlar. Foi visando introduzir estas restrições nos modelos teóricos que surgiu o conceito de saturação. Os efeitos causados pela saturação em malhas de controle são bem conhecidos. O menos nocivo deles é a perda de desempenho, podendo deixar o sistema mais lento e menos amortecido. Além disso, a saturação pode provocar o aparecimento de pontos de equilíbrio indesejados, ciclos-limite ou ainda, em um caso extremo, levar o sistema em malha fechada à instabilidade.

Motivados por este problema, uma grande quantidade de autores tem publicado trabalhos nessa área (ver, por exemplo, (Kapila and Grigoriadis, 2002), (Hu and Lin, 2001), (Tarbouriech et al., 2007), (Gomes da Silva Jr. et al., 2002) e referências nestes contidas). Em particular, podem ser encontradas abordagens para o projeto de leis de controle estabilizantes que levam em conta a priori a ocorrência da saturação. Entretanto, a maioria destes métodos preocupa-se somente com o problema de regulação. No caso de estabilização global, para um dado ponto de equilíbrio (sem perda de generalidade, considerado como a origem), é mostrado na literatura ((Sontag and Sussmann, 1990), (Burgat and Tarbouriech, 1992)) que é sempre possível encontrar uma realimentação de estados linear saturante que estabilize e melhore o desempenho do sistema em malha fechada, desde que este seja assintoticamente estável em malha aberta. Em (Hu and Lin, 2001) e (Saberi et al., 2000) são apresentados resultados para a estabilização semi-global, onde é assumido que o sistema em malha aberta seja "null controllable", ou seja, no caso discreto, todos os autovalores estão no interior ou sobre o círculo de raio unitário centrado na origem do plano complexo. Para sistemas instáveis em malha aberta, apenas a estabilização local (regional) é possível. Resultados neste sentido são apresentados em (Pittet et al., 1997), (Gomes da Silva Jr. and Tarbouriech, 2001), (Hu et al., 2002), entre outros.

Além disso, são encontrados trabalhos lidando com a chamada abordagem anti-windup. O objetivo da compensação de anti-windup é o estabelecimento de uma correção automática dos estados do controlador, quando da ocorrência da saturação, a fim de minimizar a perda de performance ou maximizar a região de atração do sistema em malha fechada (ver (Kothare et al., 1994), (Grimm et al., 2003), (Gomes da Silva Jr. and Tarbouriech, 2005) e referências). Considerando o caso de estabilidade local, em (Hu et al., 2002), é proposta uma formulação baseada em inequações matriciais bilineares (BMIs) relaxadas utilizando um modelo politópico do termo de saturação. A síntese de anti-windup estático baseada em uma condição de setor modificada é proposta em (Gomes da Silva Jr. and Tarbouriech, 2005). Neste tipo de modelagem, a estrutura da condição de setor clássica é relaxada, permitindo a obtenção de condições diretamente na forma de LMIs. Resultados relativos a compensadores dinâmicos de anti-windup são apresentados em (Grimm et al., 2003), (Gomes da Silva Jr. and Tarbouriech, 2006) e (Tarbouriech et al., 2006).

Do ponto de vista prático, o problema de seguimento de referências em sistemas com restrição de controle é de grande interesse. No início do ano 2000, Matthew C. Turner (Turner et al., 2000) já apontava a escassez de trabalhos tratando deste tema, especialmente no que se refere a abordagens no espaço de estados. Uma das metodologias mais usuais para o tratamento do problema de seguimento de referências em sistemas com atuadores saturantes baseia-se em uma realimentação de estados linear, que desconsidera a saturação, adicionada de um elemento não-linear. Neste caso, pode-se provar que, para um dado elemento não-linear e não-negativo no laço de realimentação, o sistema seguirá assintoticamente uma referência constante e ainda seu estado ficará confinado a um certo conjunto elipsoidal. Um dos trabalhos mais relevantes desta abordagem é (Lin et al., 1996), onde a teoria de regulação de saída de (Francis, 1977) é aplicada ao caso com saturação, em conjunto com a noção de estabilidade semi-global. Em (Turner et al., 2000) o trabalho de (Lin et al., 1996) é estendido para o caso multivariável e em (Hu and Lin, 2000) é caracterizada uma região de regulabilidade assintótica, isto é, um conjunto de condições iniciais do sistema e da referência/perturbação para o qual a regulação de saída ainda é possível. Recentemente, outros trabalhos nesta mesma linha foram propostos: (Su and Wu, 2006), (Teng et al., 2007) e (Pavlov et al., 2007). Outra abordagem importante baseia-se em técnicas de controle preditivo ou condicionadores de referências. Neste tipo de solução, destacamse os trabalhos de (Rawlings, 2000), (Maciejowski, 2002), (Grimm et al., 2007), (Bemporad, 1998), (Gilbert and Kolmanovsky, 2002).

Finalmente, encontra-se a linha de pesquisa na qual se in-sere o presente trabalho, que faz uso do princípio do modelo interno para garantir o seguimento de referências com erro nulo em regime permanente, além de introduzir um termo de anti-windup a fim de minimizar os efeitos da saturação. Em (Tarbouriech, Pittet and Burgat, 2000), o esquema de controle utilizado considera a introdução de uma ação integral e de um laço de anti-windup, conforme proposto inicialmente em (Krikelis and Barkas, 1984). Com o objetivo de garantir que as trajetórias do sistema em malha-fechada não deixem um certo conjunto elipsoidal, uma metodologia para a síntese de uma realimentação de estados estabilizante e de um ganho de anti-windup é proposta. Além disso, é garantido que o ponto de equilíbrio associado com o perfeito seguimento de referência está no interior da região de operação linear do sistema. Considerando um modelo politópico para de representar os efeitos da saturação no sistema, uma comparação entre a solução do problema via equações algébricas de Riccati (ARE) e LMIs é apresentada. Estes resultados foram estendidos para sistemas discretos e com referências variantes em (Tarbouriech, Queinnec and Pittet, 2000). Seguindo as mesmas idéias, mas utilizando um modelo politópico menos conservador, estes resultados foram melhorados em (Cao et al., 2004). Mesmo com condições menos conservadoras, a metodologia apresentada não permite a síntese simultânea do controlador estabilizante e do ganho anti-windup a partir de uma condição LMI, exigindo assim, a utilização de procedimentos iterativos para a solução de BMIs. O trabalho (Flores et al., 2008) segue idéias similares às propostas em (Tarbouriech, Pittet and Burgat, 2000) e (Cao et al., 2004), usando, entretanto, a condição de setor modificada proposta em (Gomes da Silva Jr. and Tarbouriech, 2005) para considerar os efeitos da saturação. Baseada nesta representação, condições LMI são obtidas diretamente, evitando-se assim a aplicação de procedimentos iterativos. Estas condições foram obtidas para um esquema de controle mais simples e com um número menor de LMIs quando comparado aos trabalhos anteriores. Além disto, um estudo sobre a possibilidade de existência de pontos de equilíbrio indesejados no interior da região invariante é realizado. Para o caso mono-entrada, é mostrado que estes pontos de equilíbrio só podem existir quando o sistema em malha aberta é assintoticamente estável.

O objetivo deste trabalho é estender os resultados de (Flores et al., 2008) para sistemas em tempo discreto. Mais uma vez, deseja-se obter a síntese simultânea de um controlador estabilizante e do ganho anti-windup, além de apresentar estimativas dos domínios de referências/perturbações e condições iniciais admissíveis. Este artigo está organizado como segue. Na Seção 2, serão apresentadas algumas considerações iniciais sobre o sistema de interesse. Na Seção 3 serão apresentados os resultados principais deste trabalho, onde serão estabelecidas condições que garantem que as trajetórias do sistema sejam limitadas para condições iniciais e referências/perturbações pertencentes a certos conjuntos admissíveis. Além disto, garante-se a existência de um ponto de equilíbrio no interior da região de comportamento linear do sistema em malha fechada, correspondente a condição de erro nulo de seguimento da referência em regime permanente. Baseado nestas condições, na Seção 4 são apresentados problemas de otimização para o cálculo do ganhos com o intuito de maximizar os conjuntos admissíveis. O comportamento da solução apresentada será ilustrado através de exemplos numéricos na Seção 5 e, por fim, serão apresentadas algumas conclusões.

Notações: A i-ésima componente do vetor x é representada por x_(i). A_(i) denota a i-ésima linha da matriz A, A(i, j) denota o elemento na linha i e coluna j de A e A^T denota sua transposta. diag{x} representa a matriz diagonal cujos elementos são dados pelo vetor x, I_m é a matriz identidade de ordem m e conv{·} denota um envelope convexo. A pseudo-inversa de uma matriz M é definida como M^# = M^T (MM^T )^-1 de tal forma que MM ^# = I_n.

2 CONSIDERAÇÕES INICIAIS

2.1 Estrutura de Controle

Considere o sistema em tempo discreto, descrito por:

sendo x

ⁿ o vetor de estados do sistema, v

^m o vetor de entradas de controle, y

^p o vetor de saídas do sistema, d

^l o vetor de perturbações constantes, r

^p o vetor de referências constantes que se deseja seguir e e

^p o vetor de erro de seguimento. As matrizes A, B, B_d e C são matrizes constantes, reais e de dimensões apropriadas.

Assume-se que o sinal de controle é saturante, isto é,

onde u(k) corresponde ao sinal calculado por um controlador. A função de saturação é definida, de maneira clássica, como

onde u_0(i) é o limite simétrico da entrada de controle v_(i) (k), ou seja, tem-se

Sobre este sistema, as seguintes hipóteses são feitas:

A1 O par (A, B) é controlável e o par (C, A) é observável;

A2 A condição (Young and Willems, 1972)

é verificada;

A3 Matrizes B e C possuem posto completo;

A4 O número de entradas é maior ou igual que o número de saídas (m > p).

A suposição A2 implica que o sistema não possui zeros de transmissão em z =1. Caso isto não se verifique, a adição de um integrador não garantirá o seguimento de referências constantes. A suposição A3 garante que não há entradas ou saídas redundantes.

Como o objetivo de controle é garantir o seguimento de referências contantes com erro nulo e rejeitar perturbações também constantes em regime permanente, uma ação integral em tempo discreto é adicionada à malha de controle através do estado

^p, dado por:

O termo E_c(sat_u0(u(k)) - u(k)) corresponde a um termo de anti-windup estático, introduzido a fim de evitar possíveis efeitos indesejados causados pela saturação do atuador. E_c

^p×m é a chamada matriz de ganho anti-windup.

Seguindo a abordagem apresentada em (Tarbouriech, Queinnec and Pittet, 2000), é feita a mudança de coordenadas do sistema para as coordenadas do erro (Krikelis and Barkas, 1984). Nestas coordenadas, o novo vetor de estados é dado por

com x₂(k)

^n-p definido por x₂(k)= M₁x(k), onde M₁

^(n-p)×n é escolhida de tal forma que

seja invertível.

A partir do sistema (1), as seguintes relações podem ser escritas:

Considerando-se uma referência constante tem-se e(k+1) = y(k + 1) - r, ou seja, y(k +1) = e(k + 1) + r. Com isto, a partir da relação (4), segue que

ou, na forma matricial,

Por suposição, M2 =[C^T M₁ ^T ]^T é invertível, o que permite que a relação acima seja escrita na forma

a qual, após a substituição de Cx(k)= e(k)+ r e x₂(k)= M₁x(k), é dada por

Da composição da equação (5) com o termo integral (2) obtém-se o sistema aumentado (6).

Assim, neste novo sistema de coordenadas, (1)-(2) pode ser reescrito como

com q =

Nota-se que, pelas suposições A1-A3, o par (A, B₁) também é controlável.

Observação 2.1 É importante notar que o novo vetor de influências externas q é agora uma combinação entre os sinais de referência e/ou perturbação agindo no sistema. Em (Cao et al., 2004) as matrizes M₂AM₂^-1E e M₂B_d são incorporadas à matriz B₃, deixando q =[rd ^T]^T. Este tipo de solução provoca uma dificuldade adicional na composição das condições na forma de LMIs, já que é necessária a existência da pseudo-inversa pela esquerda de B₃. Esta pseudo-inversa pode não existir, dependendo das matrizes A, M₂ e B_d. Conservando a formulação proposta em (Tarbouriech, Pittet and Burgat, 2000), a matriz B₃ possui a desejável propriedade B^T₃B₃ = I_n.

Considerando agora o sinal de controle como uma realimentação estática do estado z(k), segue que

levando ao seguinte sistema em malha-fechada:

Neste caso,

_w0(w(k)) = w(k) - sat_w0(w(k)) é uma não-linearidade do tipo zona-morta descentralizada (Gomes da Silva Jr. and Tarbouriech, 2005). Considerando agora = A + B₁F e= B₁ + B₂, o sistema (8) pode ser reescrito como

Na Figura 1, é ilustrada a estrutura de controle proposta.

2.2 Pontos de equilíbrio

A mudança para as coordenadas do erro traz algumas vantagens relativas à análise dos pontos de equilíbrio do sistema em malha-fechada. Como o objetivo é o seguimento de referências com erro nulo, o ponto de equilíbrio de interesse deve ser de forma

Suponha que este ponto de equilíbrio esteja no interior da região de linearidade do sistema, ou seja, z_e S(F, u₀), com

Se (A + B₁ F ) é Schur-estável, então foi provado em (Tarbouriech, Queinnec and Pittet, 2000) que o ponto de equilíbrio

é o único ponto de equilíbrio do sistema (9) no interior S(F, u₀). A fim de satisfazer ze S(F, u₀), é necessário adicionar a seguinte restrição ao vetor de referência/perturbação q:

Ainda baseado nos resultados de (Tarbouriech, Queinnec and Pittet, 2000), pode-se provar que z_e S(F, u₀) é equivalente a q S(F, u₀) onde

Assim, a relação (12) pode ser substituída por:

relação esta que independe dos ganhos F e E_c a serem determinados.

2.3 Formulação do problema

Considere

₀ um conjunto de condições iniciais e ₀ um conjunto de referências/perturbações para o sistema (9). Baseado nestes conjuntos, o seguinte problema é formulado:

Problema 2.1 Calcular o ganho da realimentação de estados F e o ganho de anti-windup E_c tais que, z(0) ₀ e r, d tais que q ₀, o ponto de equilíbrio z_e S(F, u₀) é localmente assintoticamente estável e ainda y(k) → r quando k → .

Neste caso, os conjuntos

₀ e ₀ são ditos admissíveis.

Assim, um problema de otimização implícito no Problema 2.1 é determinar as matrizes F e Ec tais que os conjuntos admissíveis Z₀ e Q₀ sejam maximizados. Neste trabalho, estes conjuntos serão considerados conjuntos elipsoidais definidos como:

onde P = P ^T > 0

^(n+p)×(n+p),v 0 e R = R^T > 0 ^(p+l)×(p+l), σ > 0 .

3 RESULTADO PRINCIPAL

Considere a matriz G ^m×(n+p)e o conjunto poliedral

Baseado no conjunto acima e na não-linearidade zona-morta descentralizada, o seguinte Lema pode ser enunciado.

Lema 3.1 (Gomes da Silva Jr. and Tarbouriech, 2006) Se z(k) S(F - G, u₀), então a relação

se verifica para qualquer matriz T ^m×mdiagonal positiva-definida.

Considerando a função candidata de Lyapunov quadrática V (k)= z(k)^T Pz(k), o seguinte teorema pode ser enunciado.

Teorema 3.1 Se existem matrizes simétricas positivas-definidas W ^(n+p)×(n+p) e R ^(p+l)×(p+l), matrizes Y ^m×(n+p), X ^m×(n+p) e M ^p×m, uma matriz diagonal positiva-definida L ^m×m e escalares positivos λ, ω, v e σ satisfazendo¹

então os ganhos F = YW ^-1 e E_c = ML^-1 são tais que, q

R, σ), o elipsóide (P, ν) é uma região de invariância positiva para o sistema (9) e (11) é o único ponto de equilíbrio na forma (10) dentro de S(F, u₀).

Prova. A satisfação de (17) implica que o elipsóide (P, ν) está incluso na região S(F - G, u₀) (Boyd et al., 1994).

Logo, para todo z(k) (P, ν) segue que a não-linearidade _u0(Fz(k)) satisfaz a condição de setor (15).

Aplicando o complemento de Schur na relação (18) e pré e pós-multiplicando o resultado por q, segue que

é verificada. A relação (19) garante então que,

q (R,σ), tem-se q S(, u₀). A partir dos resultados de (Tarbouriech, Queinnec and Pittet, 2000) apresentados na seção anterior, isto significa que o ponto de equilíbrio ze contido na região linear é único e garante erro de seguimento nulo em regime permanente.

Considere agora a função candidata de Lyapunov definida anteriormente. De (9) segue que o valor desta função em k + 1 é dado por

Para garantir a invariância do elipsóide (P, ν), basta que z(k + 1)^TPz(k + 1)^T< ν, z(k) (P, ν) e q (R, σ). Usando o S-procedure (Boyd et al., 1994), pode-se mostrar que isto é garantido se existirem escalares λ > 0 e ω > 0 verificando a relação

Suponha agora, que z(k) S(F - G, u₀). Baseado no Lema 3.1, (21) será verificada se

A relação (22) pode ser escrita em forma matricial como com

Assim, para que (22) seja satisfeita, basta que < 0 e que (P, ν) S(F - G, u₀). Esta última condição é satisfeita pela relação (17). A condição < 0 pode ser escrita como

ou, após a aplicação do complemento de Schur,

Pré e pós-multiplicando (25) por diag{P ^-1, T ^-1, I, I, I} e fazendo a substituição de variáveis W = P^-1, X = G P ^-1, Y = F P ^-1, L = T ^-1 e M = EcT ^-1 tem-se então que (25) é equivalente a (16), o que conclui a prova.

O Teorema 3.1 garante que, dado q (R, σ) e uma condição inicial no interior de (P, ν), as trajetórias do sistema (9) não deixam o elipsóide (P, ν). Além disso, é garantido que o ponto de equilíbrio associado ao seguimento de referência com erro nulo está no interior da região de linearidade e é único. Apesar de tudo isto, a existência de outros pontos de equilíbrio associados a q (R, σ) não é descartada. Tal possibilidade é ignorada em (Tarbouriech, Queinnec and Pittet, 2000) e (Cao et al., 2004). Em (Flores et al., 2008), é apresentada uma análise sobre os possíveis pontos de equilíbrio do sistema fora da região linear, para o caso monovariável em sistemas de tempo contínuo. A seguir, esta análise será estendida para sistemas de tempo discreto.

Considere as funções de transferência em malha-aberta G_v(z) e G_d(z), definidas por

Para estas funções de transferência, foram considerados valores positivos para o ganho estático do sistema, ou seja, G_v(1) > 0 e G_d(1) > 0. A dedução para G_v(1) < 0 e G_d(1) < 0 é análoga. além disso, considere z_eo como um possível ponto de equilíbrio fora da região linear. Baseado em (2), z_eo só existirá se a seguinte relação for verificada:

Seguindo a metodologia adotada em (Flores et al., 2008), a análise da existência de z_eo será apresentada considerando três casos relacionado aos autovalores da matriz A. Supõe-se que todas as condições do Teorema 3.1 são verificadas, possibilitando assim, o enunciado dos corolários que seguem.

Caso 1: A Matriz A possui todos autovalores no interior do círculo unitário (sistema em malha aberta assintoticamente estável).

Corolário 3.1 Se o sistema em malha-aberta é assintoticamente estável e se a referência r e a perturbação d são constantes e verificam a relação

então o ponto de equilíbrio z_e S(F, u₀) é o único ponto de equilíbrio no interior do elipsóide (P, v).

Prova. Suponha que o sistema (1) está saturado em qualquer um de seus limites (aqui chamado de u_e)e ainda que o ponto de equilíbrio z_eo existe. Então, a saída y_eo do sistema será dada por

Considere ainda E_c < 0 e que o sistema está saturado em seu limite superior. neste caso, u_e = u₀ e u₀ (Fz_eo) > 0. Pela relação (26), pode-se concluir que este equilíbrio existirá somente se e_e = y_eo - r < 0 ou, ainda, se

Desta equação, segue que o ponto de equilíbrio zeo só existirá se r - G_d(1)d > G_v(1)u₀, o que contradiz a relação (27).

Considere agora, E_c < 0 e que o sistema está saturado em seu limite inferior. Neste caso, u_e = -u₀ e ainda _u0(Fz_eo) < 0. Pela relação (26), pode-se concluir que este equilíbrio existirá somente se e_eo = y_eo-r > 0 ou se

Desta equação, segue que o ponto de equilíbrio z_eo só existirá se r - Gd(1)d < -Gv(1)u₀, o que também contradiz a relação (27).

É importante notar que se E_c > 0, por construção, não há a possibilidade de existência de z_eo, devido ao fato da relação (26) não possuir solução neste caso. Se o sistema está saturado em seu limite superior, então _u0(Fz_eo) > 0 e y_eo < r, ou seja, e_eo < 0, o que impossibilita a verificação de (26). O mesmo pode ser concluído quando o sistema estiver saturado em seu limite inferior.

Caso 2: A matriz A possui pelo menos um autovalor fora do círculo unitário.

Este caso corresponde a sistemas exponencialmente instáveis em malha-aberta. O seguinte corolário resume a existência de z_eo.

Corolário 3.2 Se o sistema (1) é exponencialmente instável em malha aberta, então o ponto de equilíbrio z_e S(F, u₀) é o único ponto de equilíbrio no interior do elipsóide (P, v).

Prova. O sistema nas coordenadas do erro (7) pode ser reescrito na forma

onde à = A - B₂F e = B₁ + B₂. Assim, o suposto ponto de equilíbrio z_eo fora da região linear deve ser da forma

onde u_e é o um dos limites de saturação. Fazendo, agora, a mudança de variável (k)= z(k) - z_eo no entorno do ponto de equilíbrio, segue que

Por definição, a matriz à = A - B₂F pode ser escrita, considerando F =[F₁ F₂], como

ou seja, uma matriz bloco-triangular inferior. Assim, como M₂AM₂^-1 é uma transformação de similaridade, à possuirá os mesmos autovalores de A, acrescidos dos autovalores de I_p - E_cF₂. Logo, se A é instável, então à também será, al forma que z_eo, se existir, é um ponto de equilíbrio instável e, conseqüentemente, não pode estar no interior de (P, v) pois existiriam direções invariantes (associadas aos autovetores de à fora do círculo unitário) nas quais as condições iniciais provocariam a divergência das trajetórias.

Caso 3: A Matriz A possui pelo menos um autovalor real unitário (sistema com integradores).

Para este tipo de sistema, a existência de z_eo pode ser resumida no corolário a seguir:

Corolário 3.3 Se o sistema (1) possui autovalores em z =1, então o ponto de equilíbrio z_e S(F, u₀) é o único ponto de equilíbrio no interior do elipsóide (P, v).

Prova. Neste caso, o sistema se comporta de maneira idêntica a um integrador em malha aberta sujeito a uma entrada constante. É conhecido da teoria de análise de sistemas lineares que a saída de um sistema linear em malha-aberta com polo em z =1 sujeito a uma entrada constante tende a divergir, ou seja, y(k) → quando k → . Suponha agora, que o sistema (1) está saturado em qualquer um de seus limites, admitindo o seguinte comportamento:

com sendo um vetor de entradas constantes.

Assim, partindo das suposições que os pares (A, B) e (C, A) são respectivamente controlável e observável, e de que o sistema está em equilíbrio em z_eo, a saída do sistema y(k) = Cx(k) diverge e, conseqüentemente, e(k) = y(k) - r também diverge. Como o ponto de equilíbrio z_eo, por definição, é dado por

então, o fato do sinal de erro estar divergindo contradiz a suposição de que o sistema está em equilíbrio. Por outro lado, no caso que u_e corresponde a um sinal não saturado, existe sinal de controle suficiente para cancelar os efeitos da perturbação e o ponto de equilíbrio estará na região linear, alcançada devido ao fato de que

Observação 3.1 A ocorrência destes possíveis pontos de equilíbrio fora da região de linearidade está diretamente relacionada a introdução do laço de anti-windup na malha de controle. No caso sem anti-windup (E_c =0), a relação (26) implicaria em erro nulo de seguimento também para estes pontos. Por outro lado, nesta situação, o sistema se comportaria como um sistema em malha aberta sujeito a uma entrada constante. Para plantas assintoticamente estáveis em malha aberta, a saída do sistema assumiria o valor G_v(1)u_e, apresentando assim um erro de seguimento constante, contradizendo a equação (26). Observe que, neste caso, o valor do estado do integrador tenderá ao infinito, não se verificando portanto as suposições de equilíbrio e de que as trajetórias ficam confinadas em um elipsóide invariante. Para plantas instáveis ou com integradores, a saída do sistema divergiria, o que contradiz a suposição de que o sistema está em equilíbrio (de forma análoga ao Caso 3 apresentado anteriormente).

4 PROBLEMAS DE OTIMIZAÇÃO

A seguir, baseado no teorema da seção anterior, são formula-dos alguns problemas de otimização para a obtenção dos ganhos da realimentação de estados e do laço de anti-windup:

4.1 Maximização dos elipsóides em uma dada direção

Neste caso, o objetivo é calcular F e E_c de tal forma que o tamanho dos elipsóides (P, ν) e (R, σ) sejam maximizados. O tamanho dos conjuntos (P, ν) e (R, σ) pode ser medido em relação aos conjuntos poliedrais _b e _b, _b = conv{z₁, z₂,..., z_l} e _b = conv{q₁, q₂,..., q_s}, onde os vértices z_i

^n+p, i = 1, ..., l e qj

^(p+l), j =1,..., s correspondem às direções em que deseja-se maximizá-los, conhecidas a priori.

Assim, o objetivo do problema de otimização torna-se maximizar α > 0 e β > 0 a fim de garantir α _b (P, ν) e β

_b (R, ν). Esta solução pode ser obtida a partir da resolução do seguinte problema de otimização:

Em todos os casos, considerando α = e β = , a minimização de γ e δ implica na maximização de α e β. O escalar 0 < < 1 pode ser escolhido a fim de priorizar a maximização de (P, ν) ou (R, σ). Na solução dos problemas de otimização será considerado um grid em relação às variáveis λ, ω, v e σ, fazendo com que todas as relações tornem-se LMIs.

Observação 4.1 Neste caso, os procedimentos iterativos estão unicamente relacionados aos escalares introduzidos pelo S-procedure, fazendo com que o problema de otimização seja resolvido fixando-se os mesmos sucessivamente em uma grade e avaliando a solução de problemas LMI. Em (Tarbouriech, Queinnec and Pittet, 2000) e (Cao et al., 2004) os procedimentos iterativos estão relacionados aos ganhos F e E_c, além das variáveis introduzidas pelo S-procedure. Desta forma, pelas abordagens propostas naqueles trabalhos, é impossível fazer a síntese simultânea da realimentação de estados e do laço de anti-windup. Note que este problema não ocorre na presente abordagem.

4.2 Maximização da referência admissível

A maximização da referência admissível está relacionada aos elipsóides (P, ν) e (R, σ) de forma distinta. Para o elipsóide (P, ν), esta referência, na verdade, é uma condição inicial do sistema. É fácil notar que, caso x(0) = 0 e (0) = 0, a condição inicial nas coordenadas do erro será

Assim, basta que o elipsóide (P, ν) seja maximizado em _b = conv{z₁}, z₁ =[1 00]^T , para que o valor das referências admissíveis também seja maximizado no caso em que x(0) = 0. Para o caso monovariável, após calculada a matriz P , pode-se determinar a máxima referência da seguinte forma:

Em relação ao elipsóide (R, ν) e considerando d = 0, basta que este seja maximizado em _b = conv{q₁}, q₁ = [((M₂AM₂^-1 - In)E)^T 0]^T para que a referência seja maximizada. O procedimento para a obtenção desta referência é análogo ao anterior, considerando apenas a matriz R em vez da matriz P . Ao longo deste trabalho, a referência determinada pelo elipsóide (P, ν) será chamada r_max1 ea referência determinada pelo elipsóide (R, σ) será chamada r_max2.

5 EXEMPLOS NUMÉRICOS

Nesta seção, a abordagem proposta será ilustrada com base em exemplos numéricos. Para todos os exemplos monovariáveis, as matrizes B, B_d, C e o escalar u₀ são comuns, cujos valores são dados por

Nestes casos, o que difere é apenas a matriz A. Além disso, será escolhido M₁ = [0 1], o que leva a M₂ = I₂.

Quando não indicado o contrário, serão apresentados os resultados numéricos obtidos a maximização da referência admissível. Neste caso, considerando-se x(0) = 0 e (0) = 0, os parâmetros λ, ω, v e σ indicados em cada exemplo correspondem à configuração que apresentou a maior referência possível. Neste caso, os elipsóides foram maximizados nas direções Z_b = conv{z₁} com z₁ = [1 0 0]^T e Q_b = conv{q₁} com q₁ = [((M₂AM₂^-1 - In)E)^T 0]^T para os exemplos monovariáveis e z₁ =[1 0 0 0]^T e q₁ = [((M₂AM₂^-1 - In)E)^T 0 0]^T para o exemplo multivariável.

5.1 Duplo Integrador

Este exemplo é a versão de tempo discreto do caso de dois integradores em cascata. Sua representação no espaço de estados é dada por

Neste caso, (In - M₂AM₂^-1)E = 0, fazendo com que a referência r não influencie no elipsóide (R, σ). Assim, a máxima referência admissível é definida unicamente por (P, ν) e ainda (R, σ) define exclusivamente a máxima perturbação admissível.

O problema de otimização (33) foi resolvido considerando e = 0, obtendo-se assim a solução ótima para λ = 0.9, ω = 1.0 × 10^-5, ν =1.0 × 10^-3 e σ =1.0 × 10^-5. Para estes parâmetros, a máxima referência obtida a partir de (34) foi r_max = 532.1852, com

O resultado da simulação do sistema é apresentado na Figura 2, onde nota-se que o sinal de controle satura, tanto no limite superior quanto no limite inferior, antes de entrar na região de operação linear do sistema.

5.2 Planta Estável

Para este caso, foi considerada uma planta assintoticamente estável em malha-aberta dada por

Agora, a máxima referência admissível será o menor valor entre a referência determinada por (P, ν) e aquela determinada por (R, σ). Este exemplo será utilizado para mostrar que a existência de pontos de equilíbrio indesejáveis no interior de (P, ν) deve ser levada em conta.

A resolução do problema de otimização (33) com λ = 0.5 apresentou a existência de pontos de equilíbrio fora da região linear, mas ainda no interior do elipsóide. Os resultados para λ = 0.9, ω = 1.0, ν = 1.0 × 10^-2 e σ =1.0 × 10^-6 foram

r_max1 = 2338.6 e r_max2 = 1666.1. A Figura 3 mostra a saída do sistema considerando-se uma referência r = 100 para 0 < k < 70 e r = -100 para k > 70. Pode-se notar que a saída do sistema não ultrapassa o valor G_v(1)u₀ = 15. Este exemplo justifica a análise dos pontos de equilíbrio apresentada anteriormente. Para este sistema, considerando d = 0, qualquer referência maior que r = 15 não levará a erro nulo em regime permanente.

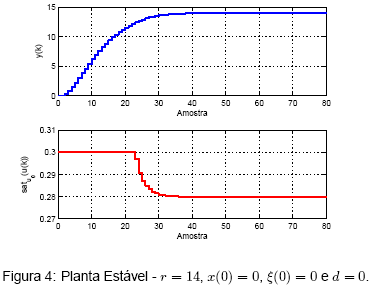
Na Figura 4 é apresentada a saída do sistema para r = 14. Pode-se notar que o sinal de controle permanece saturado por quase todo o tempo de acomodação, mas a saída acaba por convergir para a referência.

Seja agora solução do problema de otimização (33) visando a maximização do conjunto das condições iniciais. Neste caso, considerando e = 0.5 e as direções z₁ =[1 1 0]^T ₁₀₀₀ e q₁ = [((M₂AM₂^-1 - In)E)^T 0]^T , os resultados obtidos foram λ = 0.83, ω = 1, ν =1.0 × 10^-2 , 1.0 × 10^-5 x₂(0) = 502.9148 com

Na Figura 5 é apresentada a simulação do sistema pra r =5 e x(0) = [0 502.9148]^T , ambas condições admissíveis para o conjunto definido pela matriz P dada acima. Neste caso, pode-se notar que, além do elevado sobre-sinal, o sinal de controle permanece saturado por quase todo tempo de acomodação. Isto indica um grande esforço do laço de anti-windup.

Para este mesmo exemplo, foi projetado um controlador considerando E_c =0 a fim de comparar a influência do termo de anti-windup. O valor de F encontrado foi F = [-0.4618 - 1.2000 - 0.0204]. Na Figura 6, nota-se que o sistema com compensação de anti-windup acomoda-se muito mais rápido do que o controlador com E_c =0.

5.3 Planta Instável

Considere a planta com um polo instável dada por

Esta planta será utilizada para mostrar que a solução proposta é capaz de estabilizar o sistema, garantir seguimento de referência e ainda rejeitar perturbações constantes, mesmo para plantas instáveis.

Considerando-se a solução do problema (33) com e = 0.5, obtém-se λ = 0.83, ω = 1.0, ν = 1.0 × 10^-2 e σ = 1.0 × 10^-4, com

r_max1 = 19.7914 e r_max2 = 13.2174. A simulação da saída do sistema e do sinal de controle é apresentada na Figura 7.

5.4 Planta Multivariável

Este exemplo é a discretização do exemplo multivariável apresentado em (Chellaboina et al., 1999) e estudado em (Tarbouriech, Queinnec and Pittet, 2000). Sua formulação, no espaço de estados é dada por

Com esta escolha de M₁ tem-se M₂ = I₃. Este exemplo tem como objetivo mostrar a aplicabilidade da solução proposta a um sistema multivariável associado a um problema real. É importante ressaltar que os autovalores da matriz A são dados por {1.0000, 1.7229, 0.4654}.

Neste caso, sistema o apresenta uma única saída, fazendo com que o cálculo da máxima referência admissível seja feito de forma análoga ao caso monovariável. Considerando-se (33) com e = 0.5 e para λ = 0.9, ω = 0.01, ν = 1.0 ×10^-3 e σ = ν, obtém-se

r_max1 = 1793.8 e r_max2 = 104.1962. Estes resultados são ilustrados através da simulação da saída do sistema apresentada na Figura 8. Pode-se observar os dois sinais de controle oscilando entre os limites de saturação.

Considerando o sistema sujeito à perturbações, o problema de otimização (33) foi resolvido considerando as direções z₁ =[1 0 0 0]^T e q₁ = [((M₂AM₂^-1 - In)E)^T (M₂B_d)^T ]^T e ainda e = 1. Os resultados obtidos foram λ = 0.9, ω = 1.0 × 10^-2 , ν = 1.0 × 10^-3 e σ = 1.0 × 10^-3 onde

A simulação da saída do sistema para r =1, x(0) = 0 e d₁ = d₂ = 1.3509 (admissíveis para os elipsóides definidos pelas matrizes P e R dadas) é apresentada na Figura 9, onde nota-se que a mudança de referência não chega a saturar os sinais de controle, mas a perturbação faz com que a saída u₂(k) fique saturada por quase todo tempo de acomodação. Neste caso, as perturbações foram simultaneamente aplicadas para k > 60.

6 CONCLUSÕES

Neste trabalho foi apresentada uma metodologia sistemática para abordar o problema de seguimento de referências em sistemas de tempo discreto sujeitos à saturação de controle.

A maior vantagem em relação às metodologias anteriores é que as condições apresentadas são obtidas diretamente na forma de LMIs, desde que certos parâmetros sejam fixados. Assim, diferentemente de (Tarbouriech, Queinnec and Pittet, 2000) e (Cao et al., 2004), não é necessária a aplicação de esquemas iterativos envolvendo a matriz da função de Lyapunov e as matrizes de ganho a serem calculadas. Foi mostrado, através de exemplos, que a metodologia proposta se aplica tanto para sistemas mono como para sistemas multivariáveis. Para o caso monovariável, estudou-se ainda a possibilidade da existência de pontos de equilíbrios que não garantem erro de seguimento nulo em regime permanente dentro do domínio de invariância. Convém ressaltar que esta possibilidade não foi considerada em (Tarbouriech, Queinnec and Pittet, 2000) e (Cao et al., 2004).

O fato de utilizar-se uma realimentação de estados para estabilizar o sistema pode ser uma limitação em algumas aplicações práticas, mas estabelece de maneira formal uma solução para um problema complexo. A fim de superar este tipo de limitação, tem-se como perspectiva a extensão da metodologia para considerar a síntese de observadores de estado, sendo um ponto de partida o trabalho (Paim et al., 2004). Ainda sob um ponto de vista prático, a abordagem proposta, por ser baseada em LMIs, permite a extensão imediata dos resultados ao caso de sistemas apresentando incertezas politópicas ou limitadas em norma.

A extensão para referências variantes, conforme apresentado em (Tarbouriech, Queinnec and Pittet, 2000), a extensão do estudo dos pontos de equilíbrio indesejados no caso de plantas com polos imaginários sobre o círculo unitário e ainda, a extensão deste estudo para plantas multivariáveis estão sob investigação.

AGRADECIMENTOS

Os autores deste trabalho foram em parte financiados por bolsas da CAPES e CNPq, bem como por um Projeto Edital Universal do CNPq.

Artigo submetido em 27/06/2008 (Id.: 00880)

Revisado em 07/02/2009, 27/05/2009

Aceito sob recomendação do Editor Associado Prof. Takashi Yoneyama

• Bemporad, A. (1998). Reference governor for constrained nonlinear systems, IEEE Transactions on Automatic Control 43(3): 415-419.
• Boyd, S., Ghaoui, E., Feron, E. and Balakrishnan, V. (1994). Linear Matrix Inequalities in System and Control Theory, 1st edn, SIAM, Philadelphia, PA.
• Burgat, C. and Tarbouriech, S. (1992). Global stability of a class of systems with saturated controls, International Journal of Systems and Science 23: 37-56.
• Cao, Y., Lin, Z. and Ward, D. G. (2004). Anti-windup design of output tracking systems subject to actuator saturation and constant disturbances, Automatica 40(7): 1221- 1228.
• Chellaboina, V., Haddad, W. and Oh, J.-H. (1999). Fixed-structure controller design for discrete-time systems with actuator amplitude and rate saturation constraints, Proceedings of the American Control Conference (ACC'99), Vol. 3, San Diego, USA, pp. 1992- 1996.
• Flores, J. V., Eckhard, D. and Gomes da Silva Jr, J. M. (2008). On the tracking problem for linear systems subject to control saturation, Proceedings of the 17th IFAC World Congress, Seoul, Korea.
• Francis, B. (1977). The linear multivariable regulator problem, SIAM J. Control and Optimization 15(3): 486-505.
• Gilbert, E. and Kolmanovsky, I. (2002). Nonlinear tracking control in the presence of state and control constraints: a generalized reference governor, Automatica 38(12): 2063-2073.
• Gomes da Silva Jr., J. M., Paim, C. and Castelan, E. (2002). Lmi-based framework for the synthesis of saturating control laws, Revista Controle & Automação da Sociedade Brasileira de Automática 12(3): 171-177.
• Gomes da Silva Jr., J. M. and Tarbouriech, S. (2005). Antiwindup design with guaranteed regions of stability: an LMI-based approach, IEEE Transactions on Automatic Control 50(1): 106-111.
• Gomes da Silva Jr., J. M. and Tarbouriech, S. (2006). Anti-windup design with guaranteed regions of stability for discrete-time linear systems, Systems & Control Letters 55: 184-192.
• Gomes da Silva Jr., J. and Tarbouriech, S. (2001). Local stabilization of discrete-time linear systems with saturating controls: an LMI-based approach, IEEE Transactions on Automatic Control 46: 119-125.
• Grimm, G., Hatfield, J., Postlethwaite, I., Teel, A., Turner, M. and Zaccarian, L. (2003). Anti-windup for stable systems with input saturation: an LMI-based synthesis, IEEE Transactions on Automatic Control 48(9): 1500- 1525.
• Grimm, G., Messina, M. J., Tuna, S. E. and Teel, A. R. (2007). Nominally robust model predictive control with state constraints, IEEE Transactions on Automatic Control 52(10): 1856-1870.
• Hu, T. and Lin, Z. (2000). Output regulation of general linear systems with saturating actuators, Proceedings of the 39th IEEE Conference on Decision and Control (CDC'00), Vol. 4, Sydney, Australia, pp. 3242-3247.
• Hu, T. and Lin, Z. (2001). Control systems with actuator saturation: analisys and design, Birkhauser, Boston, MA.
• Hu, T., Lin, Z. and Chen, B. M. (2002). An analysis and design method for linear systems subject to actuator saturation and disturbance, Automatica 38: 351-359.
• Kapila, V. and Grigoriadis, K. (2002). Actuator Saturation Control, Marcel Dekker, Inc., New York, NY.
• Kothare, M. V., Campo, P. J., Morari, M. and Nett, C. N. (1994). A unified framework for the study of anti-windup designs, Automatica 30(12): 1869-1883.
• Krikelis, N. J. and Barkas, S. K. (1984). Design of tracking systems subject to actuator saturation and integrator wind-up., International Journal of Control 39(4): 667-682.
• Lin, Z., Stoorvogel, A. A. and Saberi, A. (1996). Output regulation for linear systems subject to input saturation, Automatica 32(1): 29-47.
• Maciejowski, J. M. (2002). Predictive control with constraints, Prentice Hall, Essex, England.
• Paim, C., Gomes da Silva Jr., J. M., Castelan, E. B. and Tarbouriech, S. (2004). Síntese de observadores de estado para sistemas lineares., Anais do XV Congresso Brasileiro de Automática, Gramado - RS, Brasil.
• Pavlov, A., van de Wouw, N. and Nijmeijer, H. (2007). Global nonlinear output regulation: convergence-based controller design, Automatica 43(3): 456-463.
• Pittet, C., Tarbouriech, S. and Burgat, C. (1997). Stability regions for linear systems with saturating controls via circle and popov criteria, Proceedings of the 36th IEEE Conference on Decision and Control (CDC'97), Vol. 5, San Diego, USA, pp. 4518-4523.
• Rawlings, J. (2000). Tutorial overview of model predictive control, IEEE Control Systems Magazine 20(3): 38-52.
• Saberi, A., Sannuti, P. and Stoorvogel, A. (2000). Control of Linear Systems with Regulation and Input Constraints, Springer-Verlag, London, UK.
• Sontag, E. D. and Sussmann, H. D. (1990). Nonlinear output feedback design for linear systems with saturation control, Proceedings of the 29th IEEE Conference on Decision and Control (CDC'90), Honolulu, USA, pp. 3414-3416.
• Su, W. and Wu, J. (2006). Performance limitation in output regulation of a nonlinear system under disturbance, Proceedings of the 45th IEEE Conference on Decision and Control (CDC'06), San Diego, USA, pp. 3254-3259.
• Tarbouriech, S., Garcia, G. and (Editors), A. H. G. (2007). Advances Strategies in Control Systems with Input and Output Constraints, Springer-Verlag New York, Inc., Secaucus, NJ.
• Tarbouriech, S., Gomes da Silva Jr., J. M. and Bender, F. A. (2006). Dynamic anti-windup synthesis for discrete-time linear systems subject to input saturation and L2 disturbances., Proceedings of the 5th IFAC Symposium on Robust Control Design, Toulousse, France, pp. 665-682.
• Tarbouriech, S., Pittet, C. and Burgat, C. (2000). Output tracking problem for systems with input saturations via nonlinear integrating actions, International Journal of Robust and Nonlinear Control 10(6): 489-512.
• Tarbouriech, S., Queinnec, I. and Pittet, C. (2000). Output-reference tracking problem for discrete-time systems with input saturations, IEEE Proceedings on Control Theory and Applications 147(4): 447-455.
• Teng, Y., Fu, Y. and Duan, G. (2007). Output regulation of singular linear systems with input saturation via nonlinear feedback, Proceedings of the 2nd IEEE Conference onIndustrial Electronics and Applications (ICIEA'07), Harbin, China, pp. 526-530.
• Turner, M. C., Postlethwaite, I. and Walker, D. J. (2000). Non-linear tracking control for multivariable constrained input linear systems, International Journal of Control 73(12): 1160-1172.
• Young, P. C. and Willems, J. C. (1972). An approach to the linear multivariable servomechanism problem, International Journal of Control 15: 961-979.

Datas de Publicação

• Publicação nesta coleção
  09 Mar 2010
• Data do Fascículo
  Fev 2010

Histórico

• Revisado
  07 Fev 2009
• Recebido
  27 Jun 2008
• Aceito
  27 Maio 2009