Utilização de filtro de transformada de fourier para a minimização de ruídos em sinais analíticos

Utilization of fourier transform filter for noise minimization in analytical signals

Fourier transform; digital filter; analytical data

DIVULGAÇÃO

Utilização de filtro de transformada de Fourier para a minimização de ruídos em sinais analíticos

Eduardo O. Cerqueira, Ronei J. Poppi*, Lauro T. Kubota

Departamento de Química Analítica - Instituto de Química - UNICAMP - CP 6154 - 13083-970 - Campinas - SP

Cesar Mello

Faculdade de Farmácia - Universidade de Franca - CP 82 - 14404-400 - Franca - SP

Recebido em 29/7/99; aceito em 22/3/00

e-mail: [e-mail]

Utilization of Fourier transform filter for noise minimization in analytical signals. Instrumental data always present some noise. The analytical data information and instrumental noise generally has different frequencies. Thus is possible to remove the noise using a digital filter based on Fourier transform and inverse Fourier transform. This procedure enhance the signal/noise ratio and consecutively increase the detection limits on instrumental analysis. The basic principle of Fourier transform filter with modifications implemented to improve its performance is presented. A numerical example, as well as a real voltammetric example are showed to demonstrate the Fourier transform filter implementation. The programs to perform the Fourier transform filter, in Matlab and Visual Basic languages, are included as appendices

Keywords: Fourier transform; digital filter, analytical data.

INTRODUÇÃO

Geralmente os sinais analíticos representam a variação de uma propriedade físico-química, de uma amostra de interesse, em função do tempo e/ou espaço. Em química analítica, os sinais mais freqüentemente encontrados são: espectros, voltamogramas, registros de um pH-metro em função do tempo, etc. Infelizmente, a maioria dos sinais provenientes de instrumentos analíticos apresentam-se contaminados (digamos, sobrepostos) com ruído, dificultando a interpretação e modelagem das propriedades associadas à estes sinais. Tipicamente o ruído instrumental afeta os limites de detecção, de decisão e de determinação, os quais são figuras de mérito extremamente importantes na avaliação do desempenho de instrumentos e métodos analíticos¹.

CLASSIFICAÇÃO DOS TIPOS DE RUÍDOS

Os tipos de ruídos podem ser classificados pelo seu espectro de freqüência (freqüência em que ocorrem), por sua distribuição de amplitude e pelo fenômeno que o origina. Vejamos alguns deles:

Ruído Jonson: Todo componente eletrônico alocado em qualquer circuito gera um ruído entre seus terminais devido à vibração térmica dos átomos. O valor desse ruído (em volts) é dado pela Equação 1.

V_ruído (RMS) = (4kTRB)^0,5

(1)

Onde k é a constante de Boltzman, T é a temperatura absoluta (K), R é a resistência do componente e B é a largura de banda (em Hz) em que o componente é capaz de monitorar. Quanto maior a faixa dinâmica de freqüências do componente, por exemplo a faixa de comprimentos de onda que um sensor espectroscópico é capaz de monitorar, maior o ruído Jonson. Esse ruído independe da freqüência monitorada, mas sim da largura de banda da faixa monitorada, ou seja, se distribui uniformemente em todo o espectro, e é assim chamado ruído branco. Este tipo de ruído torna-se particularmente crítico em detectores de radiação eletromagnética, de modo que em alguns casos resfria-se o detector, na tentativa de minimizar esse efeito.

Ruído "Shot": Devido ao fato de que a eletricidade é formada por um fluxo de elétrons, e que os mesmos, por sua vez, possuem carga discreta, a passagem dos elétrons gera uma flutuação do campo elétrico e consequentemente uma flutuação da corrente elétrica Se as cargas atuam independentemente, a flutuação da corrente é dada pela Equação 2.

I _ruído (RMS) = (2qI_dcB)^0.5

(2)

Assim como o ruído Jonson, o ruído "Shot" é gaussiano e branco (se apresenta em todas as freqüências).

Ruído "Flicker" (1/f): Os ruídos "Shot" e Jonson são formas irredutíveis de ruído, gerados de acordo com os princípios físicos. Existem uma série de ruídos que, adicionalmente aos ruídos anteriormente mencionados, interferem nas medidas analíticas. Esse tipo de ruído possui uma distribuição aproximadamente proporcional a 1/f (também chamado de ruído rosa). Há uma grande quantidade de fenômenos que geram ruídos "Flicker", como por exemplo a corrente catódica em tubos à vácuo, a flutuação da resistência em resistores, devido a constituição do material com que são feitos, etc. Não se encontrou uma explicação unificada para esses tipos de ruídos.

Interferência: Devido à interação das ondas eletromagnéticas existentes no ambiente (ondas de rádio, TV, campos magnéticos, etc.) com os instrumentos analíticos, pode ocorrer sobreposição e modulação dos sinais obtidos. Um exemplo prático desse tipo de interferência é a presença de picos com amplitude relativamente constante e freqüência de 60 Hz (e múltiplos harmônicos) adicionados ao sinal analítico. Tal interferência é comum e provem da rede elétrica.

Uma classificação, simplificada, dos tipos de ruídos instrumentais^2,3 pode ser estabelecida se levarmos em consideração as freqüências que os caracterizam. A classificação mais simples é a seguinte:

1 - Ruído de baixa freqüência.

2 - Ruído de freqüência intermediária.

3 - Ruído de alta freqüência.

O ruído de baixa freqüência caracteriza-se, na prática, por deslocamentos, derivas e tendências na linha base, de sinais analíticos. Este tipo de ruído pode ser minimizado instrumentalmente, acoplando-se a freqüência da fonte de sinais com a freqüência usada na detecção, através de um amplificador "lock-in".

Na classe de ruídos de freqüência intermediária encontramos basicamente o ruído de interferência. O ruído de interferência mais comum é o ruído de interferência da linha de energia elétrica, com freqüência fundamental da ordem de 60 Hz e suas harmônicas. Este tipo de ruído pode ser removido instrumentalmente, modulando-se a freqüência da fonte de sinais e a freqüência usada na detecção, longe da faixa de freqüências associada ao ruído de interferência. Este tipo de ruído pode também ser minimizado, com alguma facilidade, através de "softwares" projetados para esta finalidade. Veremos, claramente, como se faz isto, quando apresentarmos a teoria do filtro de transformada de Fourier.

Na última classe (classe dos ruídos de alta freqüência), encontramos o tipo de ruído mais difícil de ser tratado: o ruído branco ou ruído gaussiano. A característica marcante deste tipo de ruído é a inexistência de uma freqüência característica, mas uma distribuição de ruídos em todo o espectro de freqüências. Entretanto, pode-se minimizar, em alguns casos, este tipo de ruído através de "softwares" que apliquem filtros de transformada de Fourier, como será descrito adiante.

De um modo geral existe uma grande quantidade de tipos de ruídos, além dos mencionados, que influem nas medidas analíticas. Felizmente as mesmas geralmente se referem a propriedades físico-químicas de sistemas que não possuem grande variação com o tempo, como por exemplo a concentração de alguma espécie química, a temperatura, etc. Ou seja, os sinais relativos às medidas analíticas geralmente ocorrem em baixas freqüências, e isso possibilita a remoção de grande parte do ruído, particularmente o que ocorre em freqüências elevadas, através da utilização do filtro com transformada de Fourier.

A SUAVIZAÇÃO DE RUÍDO INSTRUMENTAL: O FILTRO DE SAVITZKY-GOLAY E O FILTRO DE MÉDIA MÓVEL.

Na tentativa de minimizar os ruídos nas medidas analíticas, tem sido elaborados vários tipos de filtros digitais. Dentre eles os mais utilizados pelos químicos analíticos são o filtro de média móvel e o filtro de Savitzky-Golay.

1- Filtro de média móvel

O filtro de média móvel⁴ tornou-se, nos últimos anos, uma ferramenta de uso comum para a suavização de ruído em sinais analíticos. O motivo para tal popularidade deve-se à sua simplicidade teórica e a sua incorporação a diversos "softwares" comerciais.

A idéia básica do método é dividir o sinal analítico em uma série de intervalos com a mesma largura, seqüencialmente e ponto à ponto, e substituir o valor do ponto central do intervalo pelo valor médio do intervalo. O processo é executado na seguinte seqüência:

1 - Define-se o número total de pontos dos dados (n1)

2 - Define-se o número de pontos do intervalo (n2), onde n2 é um número ímpar.

3 - Define-se a origem do sinal (x_i), i = INT (n2 / 2) +1.

4 - Obtém-se a média dos pontos do intervalo:

5 - Obtém-se o valor do dado filtrado como sendo a média (para cada ponto):

6 - Incrementa-se o valor de i e repete-se as etapas 4 e 5.

7 - Finaliza-se o processo quando i = n1 - INT (n2 / 2).

O filtro de média móvel é simples de entender, fácil de implementar e de execução rápida. Entretanto, os resultados que este tipo de filtro produz para sinais com picos estreitos é extremamente pobre. Tipicamente, este tipo de filtro distorce sinais analíticos, sendo esta distorção diretamente proporcional à largura do intervalo, como ilustrado para o fiagrama da Figura 1.

O filtro de média móvel reduz o ruído proporcionalmente à largura do intervalo mas, simultaneamente e proporcionalmente, distorce o sinal analítico. Assim sendo, a aplicação do filtro de média móvel fica reduzida a sinais de banda larga, em que a largura do intervalo necessário a redução do ruído não é critica.

2 - O filtro de Savitzky-Golay

O Filtro de Savitzky-Golay ^5,6 é um clássico entre os filtros de suavização de sinais analíticos e também encontra-se incorporado na maioria dos "softwares" comerciais para tratamento de dados. A idéia básica do método de Savitzky-Golay é a seguinte:

1 - Define-se a origem do sinal

2 - Define-se a largura do intervalo

3 - Define-se o ponto central do intervalo

4 - Remove-se o ponto central do conjunto de pontos do intervalo

5 - Ajusta-se através do método de mínimos quadrados, um polinômio de grau variável aos pontos restantes.

6 - Utiliza-se o polinômio para estimar o valor do ponto removido.

7 - Desloca-se o intervalo para o ponto seguinte do sinal original e repete-se o processo anterior.

O filtro de Savitzky-Golay é menos sensível à largura do intervalo pois o novo ponto, isto é, o ponto do sinal já suavizado, é obtido através do ajuste dos pontos do intervalo por um polinômio e não pela simples média dos pontos vizinhos, como ocorre com o filtro de média móvel. Esta característica possibilita que o filtro de Savitzky-Golay seja aplicado a sinais analíticos com picos estreitos, apresentando resultados superiores aos obtidos com o filtro de média móvel. Entretanto, ainda se observa distorção do sinal à medida que o número de pontos utilizado no intervalo aumenta, conforme pode ser observado na Figura 2.

Conforme descrevemos, os filtros de suavização de ruído instrumental atuam diretamente sobre o sinal analítico e não sobre as freqüências que compõem tal sinal. Esta característica torna os filtros de suavização pouco seletivos, isto é, incapazes de diferenciar o que é sinal do que é ruído e, portanto, no processo de suavização de ruído uma parte da informação útil contida no sinal é simultaneamente removida.

Felizmente, existem filtros que atuam diretamente sobre as freqüências que compõem o sinal, possibilitando a remoção seletiva de ruído. Estes filtros são conhecidos como filtros de remoção de ruído. Os mais populares são os filtros baseados em transformada de Fourier.

Remoção de ruído instrumental: Filtro de transformada de Fourier.

Filtro de transformada de Fourier

A idéia básica deste tipo de filtro é aplicar-se a transformada de Fourier direta^7-10, dada pela Equação 3, para que se obtenha o sinal analítico representado no domínio das freqüências, ou melhor, aplicamos a transformada de Fourier direta para obter o espectro de freqüências F(w), do sinal analítico.

(3)

Na Equação 3, l representa o domínio original do sinal analítico e f(l)o sinal analítico. Para espectros, l representa os comprimentos de onda; para cromatogramas ou fiagramas, l representa a variável tempo e assim por diante.

Uma vez obtido o espectro de freqüências do sinal analítico, devemos cortar as freqüências altas, visto serem estas freqüências, na grande maioria dos casos, relacionadas ao ruído instrumental.

Finalmente aplicamos a transformada de Fourier inversa, dada pela Equação 4 e recuperamos o sinal analítico inicial, livre de ruído.

(4)

O filtro de transformada de Fourier pode ser entendido como a transformada de Fourier inversa (

^-1), da transformada de Fourier direta (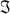) de um sinal f(l) convolvido com uma função de apodização h(l). A transformada de Fourier direta de f(l) convolvido com h(l) é dada pela Equação 5:

(5)

Uma vez que a transformada de Fourier da convolução de duas funções é o produto das transformadas, podemos escrever a Equação 6 :

(6)

No domínio das freqüências, a convolução anterior (Equação 4) se reduz à simples multiplicação das correspondentes transformadas de Fourier, como segue na Equação 7 :

(7)

em que:

no caso de um filtro passa baixa. Caso seja necessário outro tipo de filtro, deve-se alterar a função de apodização (H) conforme o desejado.

Aplicando a transformada de Fourier inversa à função F(S) obtemos o sinal f(l) livre de ruído, como mostra a Equação 8.

(8)

A seqüência de operações utilizada no processo de remoção de ruído, através da transformada de Fourier, podem ser facilmente entendidas se observarmos a Figura 3.

A menos que se possa processar utilizando álgebra simbólica, torna-se inviável computacionalmente a aplicação da transformada de Fourier, pois é impossível processar numericamente integrais com o limite de integração variando de (-¥) a (+¥). Além disso, os dados analíticos são obtidos de forma discreta (são amostrados valores relativos a cada medida), e desse modo não se tem uma função F(l), mas sim um vetor de dados discretos (amostrados experimentalmente), o que também impossibilita a utilização da transformada de Fourier. Para resolver esse problema utiliza-se a transformada discreta de Fourier, definida pela Equação 9 e pela Equação 10, e a transformada discreta inversa, definida pela Equação 11.

(9)

(10)

(11)

No caso, N é o número total de elementos do vetor de dados R(w) e I(w) se referem a parte real e imaginaria da transformada discreta de Fourier (no domínio das freqüências) e X(l) se refere ao vetor de dados analíticos (discretos), no domínio do tempo. As operações para a execução do filtro são idênticas às mencionadas com a transformada de Fourier, exceto pela utilização da transformada discreta ao invés da transformada contínua.

Existem algoritmos que executam a transformada discreta de Fourier de modo rápido e fácil, entre eles a FFT^8,9 ("Fast Fourier transform") disponível na maioria dos ambientes de computação numérica. No ^{Apêndice 1} é mostrado uma rotina para efetuar o filtro de Fourier em linguagem Matlab¹⁴ utilizando o algoritmo FFT, e no ^{Apêndice 2} é mostrada uma rotina em Visual Basic¹⁵ (versão 3.0) para efetuar o filtro diretamente a partir da definição da transformada discreta.

Tais algoritmos admitem que o vetor de dados experimentais refere-se a um período de uma função periódica, pois a transformada de Fourier é definida em todo o espaço amostral (as funções seno e cosseno possuem domínio em todo o espaço real). Isso pode gerar alguns problemas no caso em que o primeiro elemento do vetor de dados diferir muito do último. O algoritmo FFT irá modelar uma descontinuidade no vetor de dados, ou seja, irá acrescentar elementos de freqüência não encontrados nos dados experimentais. Para resolver esse problema pode-se simplesmente tomar o vetor de dados como a combinação dos dados amostrados com a reflexão especular dos mesmos, como ilustrado na Figura 4.

Desse modo o vetor de dados fica com o dobro de seu tamanho original, mas garante-se que o primeiro ponto seja igual ao último, e desse modo não se tem nenhuma descontinuidade a ser modelada. Após a filtragem, remove-se a metade posterior do vetor de dados e retorna-se ao tamanho original. Tal procedimento além de evitar o problema da descontinuidade, também garante que, a menos de aproximações numéricas, toda a informação relativa ao espectro de freqüências fique na parte real da transformada. O vetor de dados, da forma como é tomado, se refere a uma função par, e como tal é modelada apenas por uma série de funções cosseno.

O problema da presença de descontinuidades é crítico para a utilização do filtro digital por transformada de Fourier, desse modo, se houver "outliers" (pontos espúrios causados por picos de interferências e / ou erros grosseiros) no vetor de dados, os mesmos devem ser eliminados antes da utilização do filtro. Os "outliers" se caracterizam por serem pontos cujos valores diferem significativamente (até mesmo ordens de grandeza) do valor esperado para os mesmos. Para remover tais pontos, geralmente substitui-se o mesmo pela média entre seus dois vizinhos mais próximos.

A partir desse ponto, a transformada discreta de Fourier será simplesmente referida como "transformada de Fourier" para simplificar a descrição.

Para exemplificarmos a aplicação do filtro de transformada de Fourier escolhemos um sinal complexo, em que muitas freqüências estão envolvidas. Este sinal não é proveniente de nenhum processo analítico (trata-se de uma simulação computacional), mas permitirá ilustrar, de modo didático, alguns aspectos importantes do filtro de transformada de Fourier. Vejamos o exemplo.

A Figura 5 mostra o sinal inicial, que está com ruído e na Figura 6 está mostrado o espectro de freqüências deste sinal.

No espectro de freqüências pode-se observar claramente que o sinal é formado pela seguintes freqüências características:

- Sinal com freqüência igual a 5 Hz

- Sinal com freqüência igual a 10 Hz

- Freqüências altas, relativas a ruído

O próximo passo será cortar as freqüências superiores a 10 Hz. Para tanto, multiplicamos o espectro de freqüências pelo valor 1, até a freqüência 10 Hz, acima desta freqüência multiplicamos por zero. Efetuado o corte de freqüências, aplicamos a transformada de Fourier inversa e obtemos o sinal livre de ruído, como mostrado na Figura 7.

Enquanto nos filtros de suavização o fator crítico é a largura do intervalo utilizado na suavização, nos filtros de transformada de Fourier, o fator crítico é a freqüência de corte. Se o corte de freqüências for efetuado em uma posição errada, corre-se o risco de eliminar informação útil do sinal. Na Figura 8 ilustramos o que ocorreria se, por algum motivo, fosse cortado do espectro de freqüências da Figura 5, todas freqüências acima de 5 Hz e em seguida fosse aplicada a transformada de Fourier inversa.

A utilização do filtro de transformada de Fourier em dados experimentais reais é mostrada na Figura 9. Nesse caso foi obtido um voltamograma cíclico de azul de metileno adsorvido em um filme de perovisquita sintetizado em um eletrodo de vidro condutor (ITO) em meio ácido (pH ~3), utilizando uma solução 0,1 mol/L de NaNO₃ como eletrólito suporte. Foi utilizado um potenciostato sem blindagem com gaiola de Faraday, o que intensificou a ocorrência de ruídos indesejáveis aos dados analíticos.

A Figura 10 mostra o espectro de freqüências dos dados do voltamograma cíclico do azul de metileno adsorvido sobre um filme de peroviskita em ITO. Ela mostra claramente que existe interferência da rede elétrica em vários harmônicos, além de outros ruídos de freqüência elevada. Os elementos de freqüência mais baixa foram truncados pois os mesmos apresentavam intensidade da ordem de 1020, de modo que o restante do espectro foi ampliado para uma melhor visualização das freqüências relativas ao ruído experimental.

No caso de voltamogramas, a corrente elétrica é monitorada em função do potencial aplicado, que por sua vez é linear com o tempo (velocidade de varredura constante em cada rampa de potencial). O potencial aplicado varia com o tempo conforme uma função triangular, linearmente ascendente do potencial até o potencial final e linearmente descendente do potencial final até o potencial inicial, fechando um ciclo de varredura. Desse modo, conhecendo-se a velocidade de varredura em cada rampa (DV_a/Dt = 20 mV s^-1 e DV_c/Dt = -20 mV s^-1 para as varreduras anódica e catódica respectivamente), o potencial inicial (V₀ = -300 mV) e o potencial final (V_f = 300 mV), é possível representar o voltamograma como corrente em função do tempo, o que possibilita obter a transformada de Fourier em Hz (s^-1) ao invés de V^-1.

Todavia, a forma convencional, em eletroquímica, de se representar um voltamograma cíclico é traçar a corrente em função do potencial. Nesta representação é possível obter uma série de informações sobre o sistema em estudo, o que não é possível obter quando se representa um voltamograma cíclico como corrente em função do tempo. Assim sendo, adotou-se a representação dos voltamogramas na forma de corrente em função do potencial aplicado.

De um modo geral, em qualquer análise, as medidas são realizadas seqüencialmente (uma após a outra), o que gera uma dependência temporal do sinal monitorado, possibilitando assim que a transformada de Fourier seja obtida em Hz.

Pela análise do espectro de freqüências do voltamograma, mostrado na Figura 10, optou-se por filtrar o sinal relativo às freqüências acima de 50 Hz com o filtro de Fourier. Assim o voltamograma com os dados filtrados é mostrado na Figura 11.

Muitas vezes é útil trabalhar com a derivada de um sinal ao invés do dado real. A derivada, por definição, é o limite da razão da diferença entre dois pontos consecutivos pela variação entre suas abcissas, quando a diferença entre as abcissas tende a zero. Como não se consegue obter dados experimentais com variação infinitesimal, toma­se a menor variação possível das ordenadas e abcissas para o cálculo da derivada. Em dados discretos, em que os pontos são amostrados igualmente espaçados, é comum utilizar-se ao invéz da derivada, a simples diferença de ordenada entre pontos consecutivos, que a menos de uma constante multiplicativa, é numericamente igual à derivada. Essa constante é dada pela diferença entre as abcissas, e não interfere no perfil dos dados tanto para análises qualitativas quanto para quantitativas.

Se o vetor de dados possuir muito ruído, a diferenciação amplificará esse ruído, de modo que é necessário a utilização do filtro digital antes de realizar a diferenciação, caso contrário não se conseguirá trabalhar com os dados de derivada do sinal analítico. A Figura 12 mostra a derivada do voltamograma com ruído e a Figura 13 mostra a derivada dos dados do voltamograma após a utilização do filtro de transformada de Fourier .

Conforme pode ser observado na Figura 8, uma escolha errada da freqüência crítica de corte, produz uma distorção catastrófica no sinal. O sinal tratado com o filtro de transformada de Fourier, neste caso, não apresenta nenhuma relação com o sinal original.

Felizmente, a escolha da freqüência crítica é geralmente uma tarefa muito simples pois o ruído geralmente apresenta freqüência altas e o sinal útil, freqüências baixas. Na dúvida, devemos efetuar o corte bem longe das freqüência baixas. Neste caso, talvez não estejamos cortando todo o ruído, mas certamente uma parcela será eliminada e não corremos o risco de distorcer o sinal.

O grande problema do filtro de transformada de Fourier certamente não é a escolha da freqüência crítica, mas a sua aplicação a sinais não estacionários, isto é, sinais cujas freqüências características variam com tempo.

Por exemplo, um sinal pode ser composto por duas freqüências combinadas durante todo o intervalo de tempo, um segundo sinal pode possuir as mesmas duas freqüências entretanto, estas podem aparecer, no sinal, em tempos diferentes. Na Figura 14 podemos observar um sinal (Sinal 1) com duas freqüências distribuídas sobre todos os tempos. Na Figura 15 representamos um segundo sinal (Sinal 2) formado pelas mesmas freqüências do sinal anterior mas divididas em dois intervalos: na primeira metade do sinal temos somente a freqüência 10 Hz e na segunda metade a freqüência 20 Hz.

Nas Figuras 16 e 17, representou-se a transformada de Fourier dos sinais 1 e 2, respectivamente. Nesse ponto é importante observar que, por construção, o Sinal 2 só apresenta as frequências de 10 e 20 Hz. Um sinal não estácionário pode ser entendido como um somatório de sinais estacionários, em que cada termo do somatório é multiplicado por uma função limitante no tempo U(t) como mostrado na Equação 13. No caso em questão, o Sinal 2 mostrado na Figura 15 é formado pelo somatório de dois termos, como mostra a Equação 12, para um sinal amostrado entre 0 e 1 segundo.

em que a função U(t) apresenta o seguinte comportamento:

(13)

Assim, quando se aplica a transformada de Fourier em um sinal não estácionário, nos tempos em que ocorre a mudança de frequência, há uma descontinuidade na função temporal U(t), de modo que a nesse ponto a transformada insere frequências não existentes no sinal original (tenta modelar a descontinuidade da função U(t)).

Observe que os espectros de freqüência dos dois sinais (Figuras 16 e 17) apresentam as freqüências características de 10 e 20 Hz, todavia a transformada de Fourier não apresenta informação sobre a ocorrência de tais frequências no tempo. Este fato pode nos levar a uma interpretação errada a respeito do Sinal 2 pois podemos ser induzidos a pensar que o Sinal 2 possue outras frequências além das de 10 e 20 Hz, que por construção não as possui.

O resultado prático do fato descrito no parágrafo anterior é que se aplicarmos o filtro de transformada de Fourier a um sinal não estacionário, não teremos certeza das frequências que o mesmo possui, o que pode levar a uma interpretação errada na hora de fazer o corte das frequências com o filtro digital.

Este fato ocorre porque a transformada de Fourier atua no sinal como um todo e não sobre segmentos, de modo a discriminar os tempos em que as freqüências aparecem. A transformada de Fourier atua no sinal todo porque as funções utilizadas na decomposição do sinal para a obtenção do espectro de freqüências, são funções seno e cosseno que à rigor, estendem-se de menos infinito até mais infinito, isto é, a transformada de Fourier utiliza para a decomposição do sinal, funções que não possuem suporte compacto no domínio do tempo. Observe novamente a equação utilizada na transformada de Fourier direta, reescrita abaixo, e o fato da falta de suporte compacto, tornar-se-á evidente, como mostra a Equação 14.

(14)

A solução para o problema da falta de suporte compacto das funções seno e cosseno, é aplicar a transformada de Fourier a segmentos do sinal e não diretamente sobre o sinal todo, num procedimento conhecido como transformada de Fourier de pequenos intervalos⁴ (STFT, short time Fourier transform). Quando bem aplicada, a STFT fornece informações sobre os tempos em que as freqüências ocorrem. Assim sendo, devemos utilizar a STFT quando desejarmos aplicar o filtro de transformada de Fourier a sinais não estacionários. A única desvantagem prática deste procedimento é o aumento do tempo computacional. Matematicamente a STFT pode ser escrita como segue na Equação 15:

(15)

Na equação 11, o termo representa a largura do intervalo (ou janela) utilizado na STFT.

Na Figura 18 está representado o espectro de frequência do Sinal 2 (Figura 15) resolvido no tempo, obtido utilizando a STFT. Como pode ser observado, é possível discriminar no tempo as frequências que compõem o sinal. No caso em questão, observa-se que nos primeiros 500 ms o sinal é composto basicamente pela frequência de 10 Hz.Nos últimos 500 ms observa-se basicamente a frequência de 20 Hz. Na interface entre as duas frequências, aparece o efeito da mistura das duas, conforme explicado anteriormente.

Quando aplicamos a STFT para sinais não estacionários que mudam suas freqüências em intervalos de tempo muito rápidos, a largura do intervalo deve ser inversamente proporcional à mudança de freqüências do sinal, isto é, quanto mais rapidamente o sinal muda de freqüência, menor deve ser a largura do intervalo usado na STFT. Neste ponto, nos deparamos com um problema teórico muito interessante, qual seja: até quando é possível reduzir a largura do intervalo utilizado na STFT, ou melhor, com que exatidão, no domínio do tempo, as freqüências podem ser determinadas em um sinal não estacionário?

A resposta para questão anterior é dada pelo princípio da incerteza de Heisenberg^16,17. O princípio da incerteza de Heisenberg mostra que não é possível conhecer exatamente e simultaneamente, tempo (t) e freqüência (w), mas somente a seguinte relação entre estas grandezas, conforme mostrado na Equação 16.

(16)

Na prática o que ocorre é que os dados são adquiridos em intervalos de tempo discretos, e que a redução do número de pontos (no caso do STFT) resulta em menor resolução do espectro de freqüências. Este fato, nos leva ao seguinte problema de resolução: quanto menor o intervalo de tempo utilizado na STFT, pior a resolução nas freqüências e vice-versa.

Assim sendo, a transformada de Fourier nos fornece boa informação sobre as freqüências de um sinal, mas não fornece informações exatas sobre o tempo em que estas freqüências ocorrem. Já a STFT nos fornece boa informação sobre o tempo em que as freqüências ocorrem mas não fornece informações exatas sobre as freqüências. As características dos dois tipos de transformada de Fourier estão resumidas na Tabela 1.

É importante observar que quando se tem um sinal não estacionário, a aplicação da transformada de Fourier em todo o sinal dificulta o reconhecimento das frequências relativas ao ruído e das relativas ao sinal, porém se o ruído ocorre em uma região suficientemente longe das frequências que compõem o sinal, o corte das mesmas pode ser feito sem comprometer o sinal original, e desse modo a aplicação do filtro de transformada de Fourier ao invés do filtro com STFT, ainda que conceitualmente errada, leva a resultados satisfatórios.

CONCLUSÃO

Apesar das dificuldades anteriormente descritas, os filtros de ruído fundamentados em transformada de Fourier (FT ou STFT) apresentam bons resultados para a maioria dos sinais encontrados na prática e são considerados como técnica padrão, para a remoção de ruído, em diversas áreas da ciência e da engenharia. Vale salientar que em termos de dados analíticos, a grande maioria dos mesmos são estacionários, e desse modo o filtro com transformada de Fourier simples fornece resultados satisfatórios.

function [y2] = ftsmooth(x,n)

% Sintaxe: [y2] = ftsmooth(x,n);

% Entrada:

% x = Matriz de dados

% n = Número de elementos não nulos do filtro passa baixa

% Saída:

% y2 = Dados corrigidos

%

% Esse programa, toma o vetor de dados e duplica-o de modo que a segunda % metade do novo vetor de dados é igual à primeira invertida. Assim o novo vetor de % dados começa e termina no mesmo ponto, sem haver descontinuidade.

% Em seguida esse programa calcula a transformada de Fourrier dos vetores % em questão, multiplica os dados transformados por um filtro passa baixa, no caso % uma onda quadrada, e retoma os dados através da transformada inversa de % Fourrier. Finalmente o programa remove os pontos adicionados executa a % transformada de Fourrier em uma matriz ou vetor de dados

[l,c] = size(x);

for i = 1:l

x1 = x(i,:);

x2 = fliplr(x1);

x3 = [x1 x2];

% Executa o filtro pela transformada de Fourrier

ft = fft(x3(i,:));

corte = zeros(1,2*c);

corte(1,1:n) = ones(size(corte(1,1:n)));

corte(1,2*c-n:2*c) = ones(size(corte(1,2*c-n:2*c)));

ftcort = corte.*ft;

y(i,:) = real(ifft(ftcort));

% Corta os pontos anteriormente adicionados

y2(i,:) = y(i,1:c);

end

Sub Command1_Click ( )

On Error GoTo ExitSub1

'Entrada de dados via caixa de texto

N% = Val(text1.Text) 'Número total de pontos do vetor de 'dados

E% = Val(text2.Text) 'Número de freqüências consideradas 'Dimensionamento dinâmico dos vetores utilizados

ReDim X(2 *N%)

ReDim X1(2*N%)

ReDim R(2*N%)

ReDim I(2*N%)

Cls 'Clean the Screen

'Abertura do arquivo com o vetor de dados

CMDialog1.Filter = "Text Files (*.txt)|*.txt"

CMDialog1.FilterIndex = 1

CMDialog1.Action = 1

If Right$((CMDialog1.Filename), 4) = ".TXT" Or Right$((CMDialog1.Filename), 4) = ".txt" Then

NameFile = (CMDialog1.Filename)

Else

NameFile = (CMDialog1.Filename) + ".TXT"

End If

'Abre o arquivo de dados para leitura

Fileopen = FreeFile

Open (NameFile) For Input As #Fileopen

For m% = 0 To (N% - 1)

Input #Fileopen, X(m%)

Next m%

Close #Fileopen

'Duplica o vetor de dados com a imagem especular

For m% = N% To 2*N% - 1

X(m%) = X (N% - m%)

Next m%

N% = 2*N%

E% = 2*E%

'Calculando R(k) e I(k) somente para as freqüências consideradas (até E%)

Cont0 = 0

For j% = 0 To N% - 1

Cont0 = Cont0 + X(j%)

Next j%

R(0) = Cont0 / N%

For k% = 1 To E% - 1

cont1 = 0

cont2 = 0

For j% = 1 To N% - 1

cont1 = cont1 + X(j%) * Cos(2 * Pi * j% * k% / N%)

cont2 = cont2 + X(j%) * Sin(2 * Pi * j% * k% / N%)

Next j%

R(k%) = X(0) / N% + cont1 / N%

I(k%) = -cont2 / N%

Next k%

Calculando as transformações inversas também somente com as 'freqüências consideradas

cont3 = 0

For k% = 1 To E% - 1

cont3 = cont3 + R(k%)

Next k%

X1(0) = R(0) + 2 * cont3

For j% = 1 To N% - 1

cont4 = 0

For k% = 1 To E% - 1

cont4 = cont4 + R(k%) * Cos(2 * Pi * k% * j% / N%) - I(k%) * Sin(2 * Pi * k% * j% / N%)

Next k%

X1(j%) = R(0) + 2 * cont4

Next j%

'Salvando os dados corrigidos

'Abre o arquivo "resp.txt" do diretório raiz para armazenar os dados 'filtrados

fileclose = FreeFile

Open "c:\resp.txt" For Output As #fileclose

For j% = 0 To (N% /2) ­ 1

'O limite do arquivo de dados corrigidos já trunca a segunda metade do 'vetor de dados que é simétrica à primeira.

Print #fileclose, Format(X1(j%), "0.0000") 'Salva os dados 'corrigidos

Next j%

Close #fileclose

ExitSub1:

'User Set Cancel Button

Exit Sub

End Sub

• 1. Miller, J. C.; Miller, J. N.; 'Statistics for Analytical Chemistry', Ellis Horwood, Chichester, UK, 1993.
• 2. Erickson, C. L.; Lysaght, M. J.; Callis, J. B.; Anal. Chem. 1992, 64, 1155.
• 3. Bialkowski, S. E.; Anal. Chem. 1998, 60, 355.
• 4. Press, W. H.; Teukolsky, S. A.; Vetterling, W, T.; Flannery, B. P.; "Numerical Recipes in Fortram: The Art of Scientific Computing", 2^nd Edition, Cambridge University Press, New York, 1992.
• 5. Savitzky, A.; Golay, M. J. E.; Anal. Chem. 1964, 36, 1627.
• 6. Steiner, J.; Tertonia, Y.; Deltour, J.; Anal. Chem. 44, 1972.
• 7. Bracewell, R.; 'The Fast Fourier Transform and its Application',McGraw-Hill, New York, 1965.
• 8. Nussbaumer, H. J.; 'Fast Fourier Transform and Convolutions algorithms', Springer-Verlag, New Yorh, 1982.
• 9. Bloomfield, P.; 'Fourier Analysis of time series, Wiley, New York, 1976.
• 10. Canuto, C.; Hussaini, M. Y.; Quarteroni, A.; Zang, T. A.; 'Spectral methods in fluid dynamics', Springer-Verlag, New York, 1988
• 11. Gollub, J. P.; Baker, G. L.; "Chaotic Dynamics", Cambridge University Press, 1990.
• 12. Butkov, E.; "Física Matemática", Guanabara Koogam, Rio de Janeiro, 1982.
• 13. Arfken, G. B.; Weber, H. J.; "Mathematical Methods for Physicists", 4^th Edition, Academic Press, New York, 1995.
• 14. Matlab for Windows V. 4.2.1.c, The Math Works Inc., 1994.
• 15. Microsoft Visual Basic V. 3.0, Microsoft Co., 1993.
• 16. Eisberg, H.; Resnick, R.; "Quantum Physics", John Wiley & Sons, New York, 1986.
• 17. Halliday, D.; Resnick, R.; Walker, J.; "Fundamentals of Physics", 5^th Edition, John Wiley & Sons, New York, 1990.

Apêndice 1.  Rotina em linguagem Matlab para a execução do filtro de Fourier. O Matlab possui uma função interna para executar a FFT, e isso acelera a execução do filtro.

Apêndice 2.  Rotina em Visual Basic (versão 3.0) para a execução do filtro de Fourier, a partir de um arquivo com o vetor de dados em formato ASCII. Para acelerar os cálculos, essa rotina somente calcula as freqüências que serão consideradas no filtro digital. Ela pressupõe a existência de duas caixas de texto (do Visual Basic 3.0) para a entrada do número total de pontos e do número de freqüências consideradas, rotuladas com text1 e text2 respectivamente.

Datas de Publicação

• Publicação nesta coleção
  07 Dez 2000
• Data do Fascículo
  Out 2000

Histórico

• Recebido
  29 Jul 1999
• Aceito
  22 Mar 2000