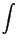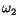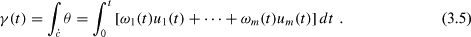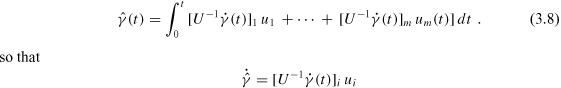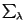Abstracts
In this note we revisit E. Cartan's address at the 1928 International Congress of Mathematicians at Bologna, Italy. The distributions considered here will be of the same class as those considered by Cartan, a special type which we call strongly or maximally non-holonomic. We set up the groundwork for using Cartan's method of equivalence (a powerful tool for obtaining invariants associated to geometrical objects), to more general non-holonomic distributions.
non-holonomic mechanics; Cartan's equivalence method; affine connections
Nesta nota revisitamos a comunicação de E. Cartan no Congresso Internacional da IMU em Bolonha, Itália. As distribuições aqui consideradas serão do mesmo tipo que as tomadas por Cartan, uma classe especial que chamamos fortemente não-holônomas. Porém, preparamos o caminho para a aplicação do método da equivalência de Cartan (uma ferramenta poderosa para a obtenção de invariantes) a distribuições mais gerais.
mecânica não holonômica; método de equivalência de Cartan; conexões afins
Non-holonomic connections following Élie Cartan
JAIR KOILLER1, PAULO R. RODRIGUES2 and PAULO PITANGA3
1Laboratório Nacional de Computação Científica,
Av. Getulio Vargas 333 - 25651-070 Petrópolis, RJ - Brazil.
2Departamento de Geometria, Instituto de Matemática,
Universidade Federal Fluminense - 24020-140 Niterói, RJ - Brazil
3Instituto de Física, Universidade Federal do Rio de Janeiro,
Cx. Postal 68528, Cidade Universitária - 21945-970, Rio de Janeiro, RJ,Brazil.
Manuscript received on February 5, 2001; accepted for publication on February 12, 2001;
presented by MANFREDO DO CARMO
ABSTRACT
In this note we revisit E. Cartan's address at the 1928 International Congress of Mathematicians at Bologna, Italy. The distributions considered here will be of the same class as those considered by Cartan, a special type which we call strongly or maximally non-holonomic. We set up the groundwork for using Cartan's method of equivalence (a powerful tool for obtaining invariants associated to geometrical objects), to more general non-holonomic distributions.
Key words: non-holonomic mechanics, Cartan's equivalence method, affine connections.
INTRODUCTION
Le vrai problème de la represéntation géométrique d'un système matériel non holonome consiste[ ... ] dans la recherche d'un schéma géométrique lié d'une maniére invariante aux propriétés mécaniques du système.
Élie Cartan
In this article we revisit E. Cartan's address (Cartan 1928) at the 1928 International Congress of Mathematicians at Bologna, Italy. The distributions considered by Cartan were of a special type which we call strongly or maximally non-holonomic. Our aim is to set up the groundwork for using Cartan's method of equivalence (a powerful tool for obtaining invariants associated to geometrical objects (Gardner 1989) to more general non-holonomic distributions.
This is a local study, but we outline some global aspects. If the configuration space Q is a manifold of dimension n, its tangent bundle T Q should admit a smooth subbundle E of dimension m, m < n. As it is well known, this imposes topological constraints on Q, see Koschorke 1981. Although we will be discussing only local invariants, hopefully these will help constructing global ones, such as special representations for the characteristic classes (Milnor and Stasheff 1974, Postnikov et al. 1999).
NOTATION. Throughout this paper we follow consistently the following convention: capital roman letters I, J, K, etc. run from 1 to n. Lower case roman characters i, j, k run from 1 to m (representing the constraint distribution). Greek characters  ,
, ,
, , etc., run from m + 1 to n. Summation over repeated indices is assumed unless otherwise stated.
, etc., run from m + 1 to n. Summation over repeated indices is assumed unless otherwise stated.
1. NON-HOLONOMIC CONNECTIONS
We fix a Riemannian metric g on Q and let  the associated Riemannian connection, torsion free and metric preserving:
the associated Riemannian connection, torsion free and metric preserving:

(1.1)
In section 8 we consider an arbitrary affine connection (see Hicks 1965) on Q. Recall that given a local frame eI on an open subset 
 , a connection
, a connection  is described by local 1-forms
is described by local 1-forms  = -
= -  such that
such that

(1.2)
The torsion tensor is T(X, Y) =  Y -
Y -  X - [X, Y] = tI(X, Y) eI and expanding the left hand side we get the structure equations
X - [X, Y] = tI(X, Y) eI and expanding the left hand side we get the structure equations
 +
+
(1.3)
As the Riemannian connection  is torsion free, tI
is torsion free, tI 0.
0.
We assume heretofore that the frame is adapted to the distribution E. This means {ei(q)} span the subspace Eq, q  Q, and the remaining {ea} span the g-orthogonal space Fq = Eq^.
Q, and the remaining {ea} span the g-orthogonal space Fq = Eq^.
DEFINITION 1.1. The (Levi-Civita) non-holonomic connection on E is defined by the rule
 (
(
 (
((1.4)

(1.5)
Here we allow X to be any vectorfield on Q, not necessarily tangent to E. Notice that for vectorfields Y, Z tangent to E, the metric-compatibility
still holds.
The motivation for Definition 1.1 is D'Alembert's principle: Consider a mechanical system with kinetic energy
g( (t),
(t), (t)) and applied forces f, subject to constraints such that
(t)) and applied forces f, subject to constraints such that  (t)
(t)  Ec(t). The constraining force
Ec(t). The constraining force 
 (t) - f is g-perpendicular to the constraint subspace Ec(t) , since it does not produce work.
(t) - f is g-perpendicular to the constraint subspace Ec(t) , since it does not produce work.
Unless otherwise mentioned, we assume there are no applied forces. The geodesic equations are given, in Cartan's approach, by

(1.6)
One may wish to see the equations explicitly. Choose a coordinate system x on 
 (x) on
(x) on  by
by

(1.7)
Write
 (
(
(1.8)
(some authors call the pk =  (
( (t)) quasivelocities).
(t)) quasivelocities).
PROPOSITION 1.2. The geodesic condition D
 = 0 yields a nonlinear system in n + m dimensions for x and p given by
= 0 yields a nonlinear system in n + m dimensions for x and p given by
 =
=
(1.9)
Here e is the R-th component ( 1
is the R-th component ( 1  R
R  n) of the k-th E-basis vector ( 1
n) of the k-th E-basis vector ( 1  k
k  m) in terms of the chosen trivialization of T Q.
m) in terms of the chosen trivialization of T Q.
The Christoffel symbols can be rewritten in terms of the m3 data c defined by
defined by
 =
=
(1.10)
In fact, compatibility with the metric (see (1.1) implies
 = -
= - 
 , and torsion free implies c
, and torsion free implies c =
= 
 -
- 
 . It follows that
. It follows that

(1.11)
Inserting into the geodesic equations, and taking into account the symmetric and anti-symmetric terms, we see that (1.9) can be rewritten as
 = -
= -
(1.12)
In this formula we already observe the interplay between the Lie bracket stucture and the metric.
2. AN EXAMPLE
Cartan's viewpoint bypasses the traditional methods in constrained dynamics where Lagrange multiplier terms are added to represent the constraint forces (just to be eliminated afterwards); see Blajer 1995 and references therein. Moreover, when using the Euler-Lagrange equations, the system of ODEs comes in implicit form unsuitable for being easily integrated numerically. In Cartan's approach all this information is embodied in the Christoffel symbols or equivalently in the structure coefficients. Cartan's approach provides an algorithmic way to derive the equations of motion for nonholonomic systems:
i) Compute the adapted orthonormal basis ei, e , say, by the Gram-Schmidt procedure.
, say, by the Gram-Schmidt procedure.
ii) Compute the structure coefficients c (x), taking Lie-brackets of the vectorfields.
(x), taking Lie-brackets of the vectorfields.
Building up on the example in Cartan (1928, section 11) we start up the derivation of the equations of motion for "Caplygin's sphere''. Details of the derivation and a theoretical analysis will be provided elsewhere.
Caplygin's sphere is a dishonest billiard ball, namely, a non homogeneous sphere of radius a and total mass m = 1 (without loss of generality), with moments of inertia I1, I2, I3, rolling without sliping on a horizontal plane. The configuration space is  2x SO (3). It is assumed that the center of mass coincides with the geometric center. Cartan considered only the homogeneous (honest) case k = I1 = I2 = I3.
2x SO (3). It is assumed that the center of mass coincides with the geometric center. Cartan considered only the homogeneous (honest) case k = I1 = I2 = I3.
We follow Arnol'd's notation (Arnol'd 1978), where capital letters denote vectors as seen from the body. We denote by  the angular velocity viewed in the space frame, and
the angular velocity viewed in the space frame, and  the angular velocity as viewed in the body frame, which we may assume attached at the principal axis of inertia. Thus R
the angular velocity as viewed in the body frame, which we may assume attached at the principal axis of inertia. Thus R  =
=  , where R
, where R  SO (3) is the attitude matrix. Intrinsically speaking, this corresponds to left translation in the Lie group SO (3). Let Q, || Q || = a, a material point in the sphere, viewed in the body frame. Thus in space
SO (3) is the attitude matrix. Intrinsically speaking, this corresponds to left translation in the Lie group SO (3). Let Q, || Q || = a, a material point in the sphere, viewed in the body frame. Thus in space
Computing the total kinetic energy
T = 
 (Q) ||
(Q) ||  dQ
dQ
yields, in the same fashion as in the rigid body with a fixed point,
 ,
,
(2.2)
where  =
=  and
and  =
=  are the cartesian components of the velocity of the geometric center.
are the cartesian components of the velocity of the geometric center.
The non-slip condition at the contact point in vector form is given by
 ,
,
(2.3)
that is,
 -
-
(2.4)
Some comments are in order. Firstly, the component  corresponds to pivoting around the contact point, and therefore is arbitrary. In fact, this distribution E of three dimensional subspaces (m = 3) in the five dimensional (n = 5) manifold R2x SO (3) is a realization of Cartan's famous "2-3-5'' distribution (see "Les systèmes de Pfaff à cinq variables et les équations aux derivées partielles du second ordre'', Cartan 1939). We observe that (2.4) could also be written in complex variables notation
corresponds to pivoting around the contact point, and therefore is arbitrary. In fact, this distribution E of three dimensional subspaces (m = 3) in the five dimensional (n = 5) manifold R2x SO (3) is a realization of Cartan's famous "2-3-5'' distribution (see "Les systèmes de Pfaff à cinq variables et les équations aux derivées partielles du second ordre'', Cartan 1939). We observe that (2.4) could also be written in complex variables notation  + i
+ i = - ai(
= - ai(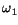 + i
+ i ), which motivates studying nonholonomic systems in the context of pseudo-holomorphic bundles.
), which motivates studying nonholonomic systems in the context of pseudo-holomorphic bundles.
It is very important in our context is to observe that the constraints define a distribution E in Q which is both right SO (3)-invariant and  2-invariant. This brings us immediatelly to the issue of integrability of nonholonomic systems, which was introduced in (Koiller 1992) and extensivelly discussed in the colletanea by Cushman and Sniatycki 1998, also see Bates and Cushman, 1999. There is a conflict between the left SO(3) invariance of the Hamiltonian (2.2) and the right SO (3) invariance of the constraints (2.4). When k = I1 = I2 = I3, the Hamiltonian is also right-invariant,
2-invariant. This brings us immediatelly to the issue of integrability of nonholonomic systems, which was introduced in (Koiller 1992) and extensivelly discussed in the colletanea by Cushman and Sniatycki 1998, also see Bates and Cushman, 1999. There is a conflict between the left SO(3) invariance of the Hamiltonian (2.2) and the right SO (3) invariance of the constraints (2.4). When k = I1 = I2 = I3, the Hamiltonian is also right-invariant,
2T = k2 ( +
+  +
+  ) +
) +  +
+  = k2 (
= k2 ( +
+  +
+  ) +
) +  +
+ 
and the problem is amenable to full right reduction and becomes easily integrable.
In fact, for the homogeneous case we use the ansatz
The adapted basis is the dual basis of the  (incidentally, we provide a correction to the coefficients given in Cartan, 1928).
(incidentally, we provide a correction to the coefficients given in Cartan, 1928).
We compute 2T = 
 /dt2:
/dt2:
2T = (A2 + D2)( +
+  ) + (B2 + a2D2)(p2 + q2) +
) + (B2 + a2D2)(p2 + q2) +  r 2 + 2(AB - aD)(
r 2 + 2(AB - aD)( q -
q -  p)
p)
The mixed term is zero provided
If we also set
 =
=
(2.8)
then
 +
+
(2.9)
with
The free parameters here are a, A and B. Another choice could be using a, as the free parameters,
as the free parameters,
 ,
,
(2.11)
 /
/
(2.12)
so that
 +
+
(2.13)
We now outline the procedure for the general case (also integrable) using Cartan's programme. To organize the calculations, we write the left invariant forms in SO (3) as

(2.14)
and we denote  (
( ) = (P, Q, R). The last entry follows the alphabet, and the reader will forgive us for mixing up the notation in the left hand side.
) = (P, Q, R). The last entry follows the alphabet, and the reader will forgive us for mixing up the notation in the left hand side.
Likewise, the right-invariant forms are

(2.15)
and we denote  (
( ) = (p, q, r). The relation R
) = (p, q, r). The relation R =
=  corresponds formally to the adjoint representation. Now, if one desires explicit formulas using, say, Euler angles, it is sufficient to parametrize R = R(
corresponds formally to the adjoint representation. Now, if one desires explicit formulas using, say, Euler angles, it is sufficient to parametrize R = R( ,
, ,
, ) and compute the left hand side of (2.14) and (2.15) in terms of the d
) and compute the left hand side of (2.14) and (2.15) in terms of the d , d
, d , d
, d .
.
It is worthy, however, to proceed as intrinsically as possible. Let f1, f2, f3 the right-invariant vectorfields in SO(3) forming the dual basis for the 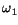 ,
, ,
, . The constraint distribution E is annihilated by the 1-forms
. The constraint distribution E is annihilated by the 1-forms
dx - a
dt , dy + adtand by inspection, we observe that the vectors

(2.16)
generate E. We complete to a basis of TQ with the vectorfields  /
/ x ,
x , /
/ y .
y .
Applying a Gram-Schmidt procedure on these vectors we get the basis ei, e , providing the starting point for Cartan's method. However, this preliminary step brings a certain amount of pain: since the inner product
, providing the starting point for Cartan's method. However, this preliminary step brings a certain amount of pain: since the inner product  ,
,  associated to T is left, but not right invariant, the orthonormal basis is neither left nor right invariant. Surprisingly, the system is still integrable. See Arnol'd et al. 1988.
associated to T is left, but not right invariant, the orthonormal basis is neither left nor right invariant. Surprisingly, the system is still integrable. See Arnol'd et al. 1988.
To orthonormalize, we need the dual basis of the  ,
, ,
, , that is, the left invariant vectorfields F1, F2, F3 such that
, that is, the left invariant vectorfields F1, F2, F3 such that
Thus in particular, f3 = R31F1 + R32F2 + R33F3 so that
 =
=
(2.18)
We define then: e1 = f3/ || f3 ||. In a similar fashion we compute e2 =  / ||
/ ||  ||, where
||, where
 =
=
(2.19)
To compute the inner product we revert to the basis of left-invariant vectorfields via (2.17) and we obtain
 = (
= (
(2.20)
It is clear that the calculations get increasingly involved but are within our powers.
3. GEOMETRIC INTERPRETATION
Direct and inverse "development'' of frames and curves were so obvious to Cartan (and for that matter, also to Levi-Civita) that he (they) did not bother to give details. Actually, inverse parallel transport seems closest to their way of thinking. We elaborate these concepts, exhibiting explicitly (Theorem 3.4 below) a system of ODEs producing at the same time, the solution of the non-holonomic system, a parallel frame along it, and a hodograph representation of the solution curves on the Euclidean space
m.3.1. DIRECT PARALLEL TRANSPORT OF A Eqo-FRAME.
A frame for Eqo
TqoQ can be transported along a curve c(t) in Q. The "novelty'' here (as stressed by Cartan): c(t) is an arbitrary curve in Q, that is (t) does not need to be tangent to E.
(t) does not need to be tangent to E.
Recall that given a tangent vector Vo = vjoej
Eqo and a curve c(t) Q, c(0) = qo, there is a unique vectorfield V(t)
Q, c(0) = qo, there is a unique vectorfield V(t)  Ec(t) , V(0) = Vo such that DV(t)
Ec(t) , V(0) = Vo such that DV(t)  0 . In fact, we are led to the linear time-dependent system of ODEs
0 . In fact, we are led to the linear time-dependent system of ODEs

(3.1)
(using D
ej = - (
( )ek and (1.6)). In particular, an orthonormal frame at Eqo is transported to Ec(t) and remains orthonormal.
)ek and (1.6)). In particular, an orthonormal frame at Eqo is transported to Ec(t) and remains orthonormal.
3.2. HODOGRAPH OF A Ec(t)-FRAME TO m.
m.
Given a curve of frames for T Q along c(t), {eI(t)}, consider the frame for Ec(t) formed by the first m vectors ei. We have
ei = - (
( ) ej -
) ej -  (
( ) ea
) ea
We develop a "mirror'' or hodograph frame {U(t) : u1(t), ... , um(t)} confined to  m
m
 O(m) given by
O(m) given by
 = -
= -
(3.2)
Equivalently (by elementary matrix algebra)
 = (
= (
(3.3)
where ui are the columns of U.
LEMMA 3.1. Let {U(0) : ui(0) = ei(0)} a frame for Eqo. The hodograph of its direct paralel transport {e1(t), ... , em(t)} along c(t) is the constant frame U(t)  U(0) = Id .
U(0) = Id .
PROOF. This is because D
ei(t) 0 iff
0 iff  (
( (t))
(t))  0.
0. 
PROPOSITION 3.2. Let U(t) a curve of frames in  m. Define a frame {
m. Define a frame { (t), ... ,
(t), ... , (t)} for Ec(t) by
(t)} for Ec(t) by
 ,
,
(3.4)
where {e1 , ... , em} is parallel along c(t). Then
i)  , ... ,
, ... , satisfies D
satisfies D
 = -
= - 
 with
with 
 = U-1
= U-1 .
.
ii) The hodograph of  , ... ,
, ... , to
to  m is U(t).
m is U(t).
PROOF. It sufficies to prove i) and it is simple:
 (
( , ... ,
, ... , )
) + (D
+ (D e1, ... , D
e1, ... , D em) U
em) U
 = (e1, ... , em) U U -1
= (e1, ... , em) U U -1 = (
= ( , ... ,
, ... , )(
)( )
)
3.3. HODOGRAPH TO
mOF A CURVE c(t) IN Q.Consider c(t), a curve in Q, c(0) = qo. As before, it is not assumed that  (t) is tangent to Ec(t). Let {eI : e1(t), ... , en(t)} a local orthonormal frame for TqQ along c(t) with {e1, ... , em} tangent to Eq. Denote
(t) is tangent to Ec(t). Let {eI : e1(t), ... , en(t)} a local orthonormal frame for TqQ along c(t) with {e1, ... , em} tangent to Eq. Denote  , I = 1, ... , n the dual basis. Construct first the hodograph {u1(t), ... , um(t)} of {e1, ... , em} to
, I = 1, ... , n the dual basis. Construct first the hodograph {u1(t), ... , um(t)} of {e1, ... , em} to  m, and then define
m, and then define
where  is an 1-form with values in
is an 1-form with values in  m given by
m given by
 =
=
(3.6)
and for short we wrote  (t) =
(t) =  (
( (t)).
(t)).
The curve  (t) in
(t) in  m
m
 m. If e1(t), ... , em(t) are parallel along c, then
m. If e1(t), ... , em(t) are parallel along c, then  (t) is given by
(t) is given by
 (t) =
(t) = 
 dt , ... ,
dt , ... ,
 dt
dt 
taking the coordinate axis of
m along u1(0) u1(t), ... , um(0)
u1(t), ... , um(0)  um(t).
um(t).
3.4. DEVELOPMENT ON Q OF A CURVE  (t)
(t) 
On the other direction,
PROPOSITION 3.3. Given a curve  (t) in
(t) in  m
m
 (t). The curve c(t) is called the development of
(t). The curve c(t) is called the development of  (t).
(t).
PROOF. First, extend an Eqo-adapted basis for TqoQ in a neighborhood q 
 , I, J = 1, ... , n. Then consider the vectorfield in
, I, J = 1, ... , n. Then consider the vectorfield in  x O (m) given by
x O (m) given by

(3.7)
Integrating this vectorfield we obtain a curve (c(t), U(t)).
We claim that the hodograph of c(t) is  (t) =
(t) =  (t) (the vectorfield was constructed precisely for that purpose). Indeed, by the previous item,
(t) (the vectorfield was constructed precisely for that purpose). Indeed, by the previous item,
which is equal to  by elementary linear algebra: if v is any vector and U any invertible matrix, v = (U-1v)iui, where ui are the columns of U (U is the matrix changing coordinates from the basis ui to the canonical basis).
by elementary linear algebra: if v is any vector and U any invertible matrix, v = (U-1v)iui, where ui are the columns of U (U is the matrix changing coordinates from the basis ui to the canonical basis). 
What if we had used a different frame  on U? We would get a system of ODEs
on U? We would get a system of ODEs

(3.9)
and we claim that Y = X so the curve c(t), is unique.
To prove this fact it equivalent to show that T = UP where P changes basis from  , i = 1, ... , m to ei, i = 1, ... , m , that is
, i = 1, ... , m to ei, i = 1, ... , m , that is
 ,
,
(3.10)
We compute

 +
+  P)
P) + P-1(U-1
+ P-1(U-1 )P = P-1
)P = P-1 + P-1(
+ P-1( )P
)P
which is indeed the gauge-theoretical rule giving the forms ( ) of the basis
) of the basis  defining T from the forms (
defining T from the forms ( ) of the basis ei.
) of the basis ei.
We can upgrade this construction to provide a parallel frame along c(t), by declaring 
 0. This gives
0. This gives
 + (
+ (
(3.11)
which could be added to system (3.7). Actually, we can take the equation for U out of that system, observing that U = P-1 (PROOF:  U-1 = - U-1
U-1 = - U-1
 )U-1 ).
)U-1 ).
THEOREM 3.4. Given a curve  (t)
(t) 

(3.12)
It gives the developed curve c(t) on Q and an attached parallel frame
 ,
,
(3.13)
For a line  (t) = t v passing through the origin in
(t) = t v passing through the origin in  m we obtain the non-holonomic geodesic starting at q with velocity
m we obtain the non-holonomic geodesic starting at q with velocity  (0) = v.
(0) = v.
3.5. HODOGRAPH OF THE D'ALEMBERT-LAGRANGE EQUATION
We elaborate on the comments of §7 in Cartan 1928 ["La trajectoire du système matériel, supposé soumis à des forces données de travail elémentaire
 , se développe suivant la trajectoire d'un point matériel de masse 1 placé dans l'espace euclidien à m dimensions et soumis à la force de composantes
, se développe suivant la trajectoire d'un point matériel de masse 1 placé dans l'espace euclidien à m dimensions et soumis à la force de composantes  .'']. Consider a mechanical system with kinetic energy T and external forces F (written in contravariant form, we lower indices using the metric so that F
.'']. Consider a mechanical system with kinetic energy T and external forces F (written in contravariant form, we lower indices using the metric so that F  TQ), subject to constraints defined by the distribution E. The non-holonomic dynamics is given by
TQ), subject to constraints defined by the distribution E. The non-holonomic dynamics is given by

(3.14)
where the right hand side is the ortogonal projection of F over E.
Let  be the hodograph of c. Fix a constant frame
be the hodograph of c. Fix a constant frame  , ... ,
, ... ,  on
on  m and write
m and write
 (t) =
(t) = 
 (t)
(t) .
.
Let  be the parallel frame along c(t) obtained in Theorem 3.4. Decompose
be the parallel frame along c(t) obtained in Theorem 3.4. Decompose
 .
.
(3.15)
COROLLARY 3.5. (Cartan 1928, §7). Equation (3.14) is equivalent to
 (
(
(3.16)
Equations (3.16) should be solved simultaneously with (3.12) and (3.13).
This approach can be helpful for setting up numerical methods, and in some cases reducing the non-holonomic system to a second order equation on
m. We also observe that F can represent non-holonomic control forces actuating over the system, as those studied in Krishnaprasad et al. 1996.4. EQUIVALENT CONNECTIONS
In this section and the next we discuss the question of whether two non-holonomic connections D and  on E have the same geodesics.
on E have the same geodesics.
Given A  GL (n - m), C
GL (n - m), C  O(m), B
O(m), B  M (m, n - m), we take
M (m, n - m), we take
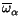 =
=
(4.1)
This is the most general change of coframes preserving the sub-Riemannian metric
 +
+
(4.2)
supported on E. The corresponding dual frame  satisfies
satisfies

(4.3)
(here, for ease of notation we place scalars after vectors).
In matrix form, we have
 =
=
(4.4)
 ,
,
(4.5)
Using matrix notation is not only convenient for the calculations, but also to set up the equivalence problem (Gardner 1989). Consider the linear group G of matrices of the form

(4.6)
The equivalence problem for sub-Riemannian geometry can be described as follows: Given coframes  = (
= (
 , ... ,
, ... ,
 )t and
)t and  = (
= (
 , ... ,
, ... ,
 )t on open sets
)t on open sets 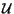 and
and  , find invariants characterizing the existence of a diffeomorphism F :
, find invariants characterizing the existence of a diffeomorphism F : 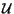
 satisfying F*
satisfying F* = g .
= g .  . For sub-Riemannian geometry, see Montgomery 2001.
. For sub-Riemannian geometry, see Montgomery 2001.
In non-holonomic geometry we are lead to a more difficult equivalence problem (see section 6.3 below). In Cartan's 1928 paper, the non-holonomic connections are characterized only for a certain type of distributions, which we will call strongly non-holonomic. Interestingly, Cartan did not work out the associated invariants, even in this case. He focused in finding a special representative in the equivalence class of connections with the same geodesics.
Consider the modified metric on Q
 =
=
(4.7)
and the associated Levi-Civita connection  . The geodesic equation is
. The geodesic equation is
 ,
,
(4.8)
To compare (4.8) and (1.6), there is no loss in generality by taking C = id. By inspection one gets:
PROPOSITION 4.1. (Cartan 1928, §5.) Fix C = id. The geodesics of D and  are the same iff
are the same iff
 (
(
(4.9)
for all T tangent to E.
5. PFAFFIAN SYSTEMS AND LIE ALGEBRAS OF VECTORFIELDS
5.1. EQUIVALENT 1-FORMS
In view of (4.9) it seems useful to introduce the following
DEFINITION 5.1. Two 1-forms 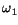 and
and  are E-equivalent if
are E-equivalent if 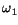 -
-  anihilates E. We write
anihilates E. We write 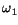
 or simply
or simply 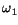
 .
.
In the C (Q)-ring of differential forms
(Q)-ring of differential forms  (Q), consider the ideal
(Q), consider the ideal  generated by the 1-forms
generated by the 1-forms 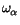 ,
, = m + 1, ... , n. We can write
= m + 1, ... , n. We can write
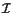
(5.1)
where the superscript ^ means "objects annihilated by''.
Clearly
 is equivalent to
is equivalent to 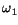 -
-  =
= 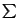 fa
fa . More generally, two k-forms
. More generally, two k-forms 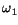 and
and  are said to be E-equivalent if their difference vanishes when one of the slots (v1, ... , vk) is taken on E. Again, this means that
are said to be E-equivalent if their difference vanishes when one of the slots (v1, ... , vk) is taken on E. Again, this means that 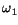 -
- 
 . (In fact, given a Pfaffian system of 1-forms on Q
. (In fact, given a Pfaffian system of 1-forms on Q
 = 0, ... ,
= 0, ... , = 0,
= 0,
one can form the ideal  on
on  (Q) generated by these forms. Every form that is annulled by the solutions of the system belongs to
(Q) generated by these forms. Every form that is annulled by the solutions of the system belongs to  , see Choquet-Bruhat et al. 1997, p.232).
, see Choquet-Bruhat et al. 1997, p.232).
If
 it does not necessarily follow that dd
it does not necessarily follow that dd . For the later to happen, the former must be equivalent over a larger subspace, (
. For the later to happen, the former must be equivalent over a larger subspace, ( 1)^E which we now describe.
1)^E which we now describe.
5.2. FILTRATIONS IN T Q AND IN T *Q
For background and a comprehensive review of the theory, see, e.g., Vershik and Gershkovich 1994. Let  a Pfaffian system.
a Pfaffian system.
DEFINITION 5.2. The derived system D( ) is
) is
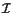
(5.2)
One constructs (see Bryant et al. 1991) the decreasing filtration
...
(2)(1)(0) =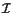
defined inductively by
(k + 1) = ( (k))1.
(k))1.
Here  is thought as a submodule over C
is thought as a submodule over C (Q) consisting of all 1-forms generated by the
(Q) consisting of all 1-forms generated by the  . We assume all have constant rank. The filtration eventually stabilizes after a finite number of inclusions, and we denote this space
. We assume all have constant rank. The filtration eventually stabilizes after a finite number of inclusions, and we denote this space 
 final. By Frobenius theorem, the Pfaffian system
final. By Frobenius theorem, the Pfaffian system 
 final is integrable. Fix a leaf S and consider the pull back of the filtration. That is, we pull back all forms by the inclusion j : S
final is integrable. Fix a leaf S and consider the pull back of the filtration. That is, we pull back all forms by the inclusion j : S  Q. The filtration associated to j*
Q. The filtration associated to j* stabilizes at zero.
stabilizes at zero.
There is a dual viewpoint, more commonly used in non-holonomic control theory (Li Z and Canny 1993): given a distribution E in TQ one considers an increasing filtration
Eo = E  E1
E1
Two (different) options are used by workers in this area:
1) Ei = Ei - 1 + [Ei - 1, Ei - 1] .
2) Ei = Ei - 1 + [Eo, Ei - 1] = Ei - 1 +  [Ej, Ek] .
[Ej, Ek] .
We follow the first option, which is recursive, and yields faster growth vectors. Moreover, the following fundamental duality result is easy to prove:
LEMMA 5.3.
(1) = E1^ (equivalently E1 = ( (1))^ ).
(1))^ ).
PROOF. Let X, Y, Z  E. Observe that
E. Observe that 
 (X + [Y, Z]) = 0 .
(X + [Y, Z]) = 0 .
Well,  (X) = 0 by default and (the correct signs do not matter)
(X) = 0 by default and (the correct signs do not matter)
 [Y, Z] =
[Y, Z] =  d
d (Y, Z)
(Y, Z) Z
Z (Y)
(Y) Y
Y (Z) = 0
(Z) = 0
as  (Y) =
(Y) =  (Z)
(Z)  0 because
0 because 
 and d
and d (Y, Z) = 0 because
(Y, Z) = 0 because  1.
1. 
6. MAIN RESULT
6.1. STRONGLY NON-HOLONOMIC DISTRIBUTIONS
The main question to be addressed in the local theory is the following. Assume that the geodesics of two Levi-Civita non-holonomic connections D and  are the same. Proposition 4.1 says that a necessary and sufficient condition for this to happen is
are the same. Proposition 4.1 says that a necessary and sufficient condition for this to happen is 
 .
.
What are the implications of this condition in terms of the original coframes  = (
= (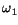 , ... ,
, ... , ) and
) and  = (
= ( , ... ,
, ... , )? The answer is that it depends on the type of distribution E.
)? The answer is that it depends on the type of distribution E.
One extreme: suppose E is integrable, that is  (1) =
(1) =  . There is a foliation of Q by m-dimensional manifolds whose tangent spaces are the subspaces Eq. Then it is clear that there are no further conditions. We can change the complement F = E^ without any restriction, and the metric there. In fact, we can fix a leaf S and the Levi-Civita connection on S will coincide with the projected connection, no matter what
. There is a foliation of Q by m-dimensional manifolds whose tangent spaces are the subspaces Eq. Then it is clear that there are no further conditions. We can change the complement F = E^ without any restriction, and the metric there. In fact, we can fix a leaf S and the Levi-Civita connection on S will coincide with the projected connection, no matter what  is outside E.
is outside E.
The other extreme is the case studied in Cartan 1928:
DEFINITION 6.1. We say that the distribution E is of the strongly or maximally non-holonomic type if the derived Pfaffian system associated to E is zero.
In the modern terminology one says that the nonholonomicity degree is 2. We now prove
THEOREM 6.2. (Cartan 1928, §5.) In the strongly nonholomic case, the metrics  and g must have the same complementary subspaces. In other words: B
and g must have the same complementary subspaces. In other words: B  0. Thus
0. Thus
F = E^
is intrinsecally defined.
PROOF. Cartan used an argument that we found not so easy to decipher (see (6.6) on section 6.2 below). Thus we prefer to use a different argument to show that B  0. We start with the structure equation
0. We start with the structure equation
d = -
= - 
 -
- 
Since
 and
and 
 (see Equation (4.1) with C = I) this implies
(see Equation (4.1) with C = I) this implies

(6.1)
Now Equation (6.4) yields
d = d
= d + dBi
+ dBi
 + Bi
+ Bi d
d
and this inocently looking expression, together with (6.1) yields

(6.2)
Hence if the distribution is of strongly non-holonomic type then B  0.
0. 
6.2. DIGRESSION
The following calculations are actually never explicitly written in Cartan 1928, it seems that Cartan does something equivalent to them mentally. A caveat: the connection forms  are antisymmetric in the indices I, J but in general this will not be the case for the forms
are antisymmetric in the indices I, J but in general this will not be the case for the forms  below. If desired, they will have to be antisymmetrized (a posteriori).
below. If desired, they will have to be antisymmetrized (a posteriori).
We begin by differentiating
The block (-  ) is given by
) is given by
(-  ) = - C(
) = - C( )C-1 + B(
)C-1 + B( )C-1 + dC C-1
)C-1 + dC C-1
We can take C = const. = id since we are not changing the subspace E. In this case
 =
=
(6.4)
and
 ) = (-
) = (-
(6.5)
From equation (6.5), Cartan observed:
PROPOSITION 6.3. The condition
 is equivalent to
is equivalent to
 )
)
(6.6)
Cartan showed that under the hypothesis of the derived system being zero (6.6) implies B  0. This follows from applying matrix B to the structure equations
0. This follows from applying matrix B to the structure equations
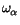 = -
= -
(6.7)
Actually Cartan gave the expression (Cartan 1928, section §4) like
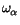 =
=
(6.8)
from which (6.2) gives

(6.9)
which is assumed to have only the trivial solution ["Nous allons, das ce qui suit, nous borner au cas où les équations homogènes
cjk u
u = 0 aux n - m inconnues um + 1, ... , un n'admettent que la solution ua = 0. Cela revient à dire que le système dérivé se reduit à zéro'' (Cartan 1928, section §5)].
= 0 aux n - m inconnues um + 1, ... , un n'admettent que la solution ua = 0. Cela revient à dire que le système dérivé se reduit à zéro'' (Cartan 1928, section §5)].
6.3. EQUIVALENCE PROBLEM FOR NON-HOLONOMIC GEOMETRY
The method of equivalence is advertised by Cartan in the 1928 address ["La recherche des invariants d'un systeme de d'éxpressions de Pfaff vis-à-vis d'un certain groupe de substituitions linéaires effectuées sur ces expressions'' (Cartan 1928, section 4)], but interestingly, he did not apply the method to its full power. We now outline the equivalence problem.
Recall that for general distributions (6.2) leads to the condition
Bi
The derivation was done in the particular case where C = id. But this is not a restriction. Replacing  = (ei)C by the ei does not change the non-holonomic geometry and leads to the transition matrix
= (ei)C by the ei does not change the non-holonomic geometry and leads to the transition matrix

(6.10)
Then ( ) = (
) = ( ) + C-1B(
) + C-1B(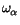 ) and (6.2) becomes
) and (6.2) becomes
C-1B(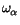 )
) 
and C-1 can be removed because  (1) is a module over the functions on Q.
(1) is a module over the functions on Q.
In spite of Cartan's caveat ["Si le système dérivé n'est pas identiquement nul, le problème de la représentation géométrique du système matériel devient plus compliqué. On est obligé de distinguer différent cas, dans chacun desquels, par des conventions plus ou moins artificielles, on peut arriver à trouver un schéma géométrique approprié. Nous n'entreprendrons pas cette étude génerale, dont l'interét géométrique sévanouirait rapidement à mesure que les cas envisagés deviendraient plus compliqués'' (Cartan 1928, §11)], we hope to raise interest in further research on the equivalence problem for non-holonomic geometry:
Given coframes ( )
) = (
= ( ,
, )
) and (
and ( )
) = (
= ( ,
, )
) on open sets
on open sets 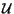 and
and  , find invariants characterizing the existence of a diffeomorphism F
, find invariants characterizing the existence of a diffeomorphism F
 satisfying F*
satisfying F* = g .
= g .  , where the substitutions are of the form
, where the substitutions are of the form

(6.11)
with
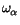 )
)
(6.12)
We recall that
 (T*Q) is the annihilator of E. The greek indices can be further decomposed into two parts:
(T*Q) is the annihilator of E. The greek indices can be further decomposed into two parts:
capital greek letters  = 1, ... , r representing forms
= 1, ... , r representing forms 
lower case greek letters  = m + r + 1, ... , n , where r = dim
= m + r + 1, ... , n , where r = dim  (1) , 0
(1) , 0  r
r  n - m .
n - m .
Matrix B can be written B = (B1, B2) where the first is m x r and the second is m x (n - m - r). Condition (6.2) is equivalent to B2 0 and our choice of basis implies that
0 and our choice of basis implies that
d involve only the
involve only the  's and the
's and the 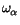 's; d
's; d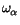 involve at least one of the
involve at least one of the  .
.
The group of substitutions consist of matrices of the form

(6.13)
In terms of frames we have
 )C
)C
 )
)  )B1 + (
)B1 + ( )Ao + (
)Ao + ( )A1
)A1
 )A2
)A2
which in particular shows:
THEOREM 6.4. With the above notations, we have:
i) (ei, ea) generate an intrinsic subspace [ (1)]^, annihilated by
(1)]^, annihilated by
ii) The eagenerate an intrinsic orthogonal complement F of E in [ (1)]^.
(1)]^.
iii) There is complete freedom to choose the e
to complete the full frame for TqQ .7. NON-HOLONOMIC TORSIONS AND CURVATURES
In this section we come back to the strongly non-holonomic case. Since B = 0 (and as we can take C = id) we have
 =
=
(7.1)
We look at the original structure equations for the  :
:
 = (
= (
(7.2)
where  = -
= -  and we expand
and we expand  as a certain combination of the coframe basis
as a certain combination of the coframe basis  ,
, (at this point there is still freedom to choose the matrix A defining the
(at this point there is still freedom to choose the matrix A defining the  ). The result is of the form
). The result is of the form
d = -
= - 
 +
+ 
 + s
+ s mi
mi
 .
.
We now use to our advantage the condition
 of Proposition 4.1. We can modify
of Proposition 4.1. We can modify
There is a unique choice of p's making the  's symmetrical, namely
's symmetrical, namely
 =
=
(7.4)
Summarizing, we have the Cartan structure equations for strongly non-holonomic connections:
THEOREM 7.1. (Cartan 1928, §6). Consider the non-holonomic connection  with connection forms (1.4) modified as in (7.3). Then
with connection forms (1.4) modified as in (7.3). Then  and D have the same geodesics and
and D have the same geodesics and
 = -
= -
(7.5)
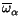 =
=
(7.6)
The forms  = -
= -  are uniquely defined by the symmetry requirement
are uniquely defined by the symmetry requirement
 =
=
(7.7)
Cartan did not invest on computing curvatures ["En même temps qu'une torsion, le développement comporte une courbure, dont il est inutile d'e'crire l'expression analytique'' (Cartan 1928, §8). We take Cartan's words as dogma, perhaps to be subverted in future work]. The curvature forms for the connection  would be helpful to compute characteristic classes of the bundle E
would be helpful to compute characteristic classes of the bundle E  Q.
Q.
7.1. A CANONICAL CHOICE OF METRIC IN F = E^
Assuming the strongly non-holonomic hypothesis, (6.9) yields for each pair of indices j  k,
k,

(7.8)
Interpreted as a linear system for the ua, this in particular implies
m(m - 1) n - m or m(m + 1)
n - m or m(m + 1)  2n .
2n .
We now work on the change of coframes
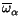 =
=
(7.9)
The differentials of the latter are given by:
d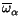 = Aa
= Aa d
d +
+  mod
mod 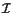
d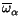 = Aa
= Aa (-
(- 
 -
- 
 ) +
) +  mod
mod 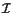
Now,
 =
=
(7.10)
so that
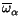 =
=
(7.11)
with
 =
=
(7.12)
We can choose matrix A uniquely by a Gram-Schmidt procedure on the n - m linearly independent vectors (cij )
)  = m + 1, ... , n in
= m + 1, ... , n in  (m(m-1)/2).
(m(m-1)/2).
Thus we obtain the conditions on the bivectors (Cartan's terminology):

(7.13)
From this point on, in order to maintain the ortonormality conditions, the change of coframes must be restricted to A  O(n - m). Hence we get
O(n - m). Hence we get
THEOREM 7.2. (Cartan 1928, §9). Assume the strongly non-holonomic case. The conditions (7.13) define uniquely a metric  on TQ = E
on TQ = E  F.
F.
7.2. GEOMETRIC INTERPRETATION OF TORSION
Recall the
m = Eqo valued 1-form given by (3.6)
given by (3.6)
 = "d
= "d " =
" =  uj
uj
which is the integrand of (3.5). The quotes indicate that this is a loose notation, "d " is not exact. Indeed, we compute
" is not exact. Indeed, we compute
d = d
= d
 .
.
Now, duj = -  uk by construction, so by Proposition 7.1
uk by construction, so by Proposition 7.1
 =
=
(7.14)
In the strongly non-holonomic case, Theorem 7.1 gives
 =
=
(7.15)
PROPOSITION 7.3. (Cartan 1928, §8). Consider an infinitesimal parallelogram in Q spanned by vectors u, v in TqQ, and the associated infinitesimal variation d (u, v) in
(u, v) in  m. If u, v belong to Eq there is no variation in
m. If u, v belong to Eq there is no variation in  m after the cycle. For u
m after the cycle. For u  Eq and v
Eq and v  Eq^ = Fq the variation is given by the torsion coefficients
Eq^ = Fq the variation is given by the torsion coefficients  's. For u, v
's. For u, v  Fq the variation is determined by the coefficients s
Fq the variation is determined by the coefficients s m i's.
m i's.
The symmetry (7.7) has the following interpretation:
 (
(
(7.16)
with u, v  Eq, n
Eq, n  Fq.
Fq.
One can consider the non-holonomic connection on F associated to the metric  . Moreover, one can repeat the procedure in Theorem 7.1. Write
. Moreover, one can repeat the procedure in Theorem 7.1. Write
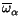 =
=
(7.17)
where the ambiguity on the  's can be removed by changing to another
's can be removed by changing to another  =
=  +
+  mod[
mod[ ] and imposing the symmetry
] and imposing the symmetry  =
=  and the antisymmetry
and the antisymmetry  = -
= -  .
.
Mutatis mutandis, the geometric interpretation of the torsion coefficients  's and cija's is analogous. In particular, there is no torsion for pairs u, v
's and cija's is analogous. In particular, there is no torsion for pairs u, v F.
F.
It seems that these geometric interpretations were forgotten by the geometers from the 60's on. For instance, in the very influential lectures (Hicks 1965, p. 59), it is written: "as far as we know, there is no nice motivation for the word torsion''.
7.3. THE CASE WHERE F IS INTEGRABLE
When the torsion coefficients in (7.5) all vanish, d =
= 
 , then all the forms d
, then all the forms d belong to the ideal
belong to the ideal
 = [
= [
(7.18)
so by Frobenius theorem, the distribution F =  ^ is integrable.
^ is integrable.
One can construct a local fibration
B, whose fibers are (pieces of) F leaves. Choose coordinates (q1, ... , qm, qm + 1, qn) on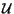 , such that (q1, ... , qm) are coordinates on B and the fibration is (q1, ... , qm, qm + 1, qn)
, such that (q1, ... , qm) are coordinates on B and the fibration is (q1, ... , qm, qm + 1, qn)  (q1, ... , qm). The distribution E will be given by
(q1, ... , qm). The distribution E will be given by
If the functions bai do not depend on the last m - n coordinates, we have locally an  m - n action on
m - n action on 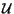
-
Given (
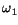 ,
,... ,
 ) a coframe on
) a coframe on 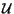 , find a Lie group
, find a Lie group G of dimension
n -
m, a diffeomorphism
F
P =
B
x
 and a connection on the principal bundle
and a connection on the principal bundle P such that the distribution
E
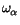 = 0 on
= 0 on 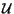 corresponds to the horizontal spaces of the connection on P.
corresponds to the horizontal spaces of the connection on P. -
Add to the previous a Riemannian metric
g on
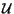 and assume that it is
and assume that it is G-equivariant.
-
Same, requiring that the vertical and horizontal spaces are
g-orthogonal. In other words, the vertical spaces
b
x
 correspond to the leaves of
correspond to the leaves of F.
Case 2) was considered in (Koiller 1992). The non-holonomic connection on E projects to a connection on B. Alternatively, it is also possible to use the Levi-Civita riemannian connection DB on B, relative to the projected metric. We get an equation of the form D
 = K(b) .
= K(b) .  where K is antisymmetric. The force in the right hand side is gyroscopic (does not produce work).
where K is antisymmetric. The force in the right hand side is gyroscopic (does not produce work).
This force K vanishes in case 3). This seems to be what Cartan had in mind in the abelian case ["Si alors dans l'expression de la force vive du système on tient compte des équations des liaisons, on obtient une forme quadratique en q'1, ... , q'm, avec des coefficients fonctions de q1, ... , qm. On peut appliquer les équations de Lagrange ordinnaires.'' (Cartan 1928, §10)]. We observe that in the example of Caplygin's sphere, we have the principal bundle with connection  2x SO(3)
2x SO(3)  SO(3), and the vertical and horizontal spaces are not orthogonal. A "non-holonomic force'' is present in the reduced system even in Cartan's homogeneous case.
SO(3), and the vertical and horizontal spaces are not orthogonal. A "non-holonomic force'' is present in the reduced system even in Cartan's homogeneous case.
8. RESTRICTED CONNECTIONS
In this section we adopt an "internal'' point of view, as opposed to the "extrinsic'' approach of the preceding ones. It is quite fragmentary and tentative, aiming to propose directions for future work. We change the notation for the configuration space, which will be denoted M.
Consider a subbundle E  M of TM, and a vector bundle H
M of TM, and a vector bundle H  M.
M.
DEFINITION 8.1. An E-connection D on H is an operator DXs for X section of E and s section of H, satisfying:
D is  -linear in X and s and C
-linear in X and s and C (M)-linear in X.
(M)-linear in X.
D is Leibnitzian in s:
DXfs = X( f )s + fDXs .
To emphasize the fact that X  E, we also call this object an E- restricted connection. When H = E an E-restricted connection on E will be called a non-holonomic connection on E.
E, we also call this object an E- restricted connection. When H = E an E-restricted connection on E will be called a non-holonomic connection on E.
A comment is in order. This definition seems natural here but we have searched the literature and have not found it. In fact, given a vector bundle H  M, the usual notion of a connection D on H (see e.g., Milnor and Stasheff 1974, appendix C) means a TM-connection on H, in the sense of our Definition 8.1. We will call those full connections. That is, X is allowed to be any section of TM, so one is able to covariantly differentiate allong any curve c(t) in M. The difference in Def 8.1 is that the covariant differention is defined just for curves with
M, the usual notion of a connection D on H (see e.g., Milnor and Stasheff 1974, appendix C) means a TM-connection on H, in the sense of our Definition 8.1. We will call those full connections. That is, X is allowed to be any section of TM, so one is able to covariantly differentiate allong any curve c(t) in M. The difference in Def 8.1 is that the covariant differention is defined just for curves with 
Given a full connection, evidently, it can the restricted to E or F. Given a (restricted) E-connection on H, can it always be extended to a (full) TM-connection? The answer is yes. Consider the following "cut-and-paste'' or "genetic engineering'' operations:
Let

(8.1)
be a Whitney sum decomposition with projection operators denoted by P (over E parallel to F) and Q (over F parallel to E).
i) Given a (full) connection DXY on TM, it induces full connections D1 on E and D2 on F, by restricting Y to one of the factors (say, E) and projecting the covariant derivative DXY over this factor. Since full connections are plentiful, so are restricted ones.
ii) Given D1, D2 E-restricted (F-restricted, respectively) connections on H, it is obvious that DXs = D
s + Ds defines a full connection on H.PROPOSITION 8.2. Given a non-holonomic connection D(E, E) on E, and D(F, E) an F-connection on E, the rule

(8.2)
defines a TM connection on E extending D. Here P and Q are respectively the projections on E (resp. F) along F (resp. E).
REMARK 8.3. However, given an E-restricted connection D1 in E and an F-restricted connection D2 in F, the rule
DXY = D
Y1 + DY2fails to define a connection in TM, because
X1(f )Y1 + X2(f )Y2
X(f )Y.The equivalence problem can be rephrased as follows: characterize the class of full connections D on M such that their non-holonomic restrictions DE = D(E, E)have the same geodesics.
8.1. PARALLEL TRANSPORT AND GEODESICS
The basic facts about TM-connections (see Hicks 1965), chapter 5) hold also for E-restricted connections. For instance,
-
(
D
X
Y)
m depends only on the values of
Y
H along any curve
c(
t)
M with
 (0) =
(0) = X
m.
-
Parallel transport of a vector
h
o
H
m along a curve
c(
t)
M with
E.
We slightly change the usual proofs (Hicks 1965). Take a local basis {hj}, j = 1, ... , p trivializing H over a neighborhood U  M and vectorfields e1, ... , eq on U
M and vectorfields e1, ... , eq on U  M generating E. Here q is the dimension of the fiber of E and p the dimension of the fiber of H. We define p2q functions
M generating E. Here q is the dimension of the fiber of E and p the dimension of the fiber of H. We define p2q functions 
 (1
(1  i, j
i, j  p, 1
p, 1  k
k  q) on U by
q) on U by

(8.3)
Write
We search aj(t) such that h(t) = 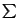 aj(t)hj satisfies
aj(t)hj satisfies
D
h(c(t)) 0.
0.
We get a linear system of ODEs in p-dimensions

(8.4)
where
 (t) =
(t) = 
 (c(t)) .
(c(t)) .
Recall that an E-connection on itself (that is, H = E) is called a non-holonomic connection on E. The equation D
 = 0 gives a nonlinear system in n + p dimensions (where n is the dimension of M and p = q is the dimension of E) for x and a given by
= 0 gives a nonlinear system in n + p dimensions (where n is the dimension of M and p = q is the dimension of E) for x and a given by

(8.5)
Here ekr is the r - component ( 1  r
r  n) of the k-th E-basis vector ( 1
n) of the k-th E-basis vector ( 1  k
k  p) in terms of a standard trivialization of TM.
p) in terms of a standard trivialization of TM.
8.2. TORSION AND CURVATURE
Let D, two (full) TM-connections, and DE,
two (full) TM-connections, and DE, their restrictions as E-connections along F. Consider the difference tensor on TM
their restrictions as E-connections along F. Consider the difference tensor on TM
B(X, Y) =  Y - DXY , X, Y
Y - DXY , X, Y 
 (TM) .
(TM) .
Clearly B is C (M)-linear in both slots. Decompose B = S + A into symmetric and skew-symmetric pieces:
(M)-linear in both slots. Decompose B = S + A into symmetric and skew-symmetric pieces:
 [
[
(8.6)
Consider also the torsions
 (
(
(8.7)
It is easy to verify
 (
(
(8.8)
These objects clearly make sense in the restricted version. Recall (Hicks 1965, 6.5) the notion of torsion associated to a (1, 1) tensor P ( m  M
M  Pm
Pm
Here we take for operator P the projection over E along F. In the context of restricted connections X, Y are vectorfields in E.
DEFINITION 8.4. Let BE the restriction of B to E, with values projected on E along F, and similarly define SE, AE. Define the restricted torsion by
 (
(
(8.10)
The latter is a Em valued tensor (vm, wm)  Emx Em
Emx Em
 (vm, wm)
(vm, wm)
THEOREM 8.5. The following are equivalent:
a) DE and  have the same E-geodesics.
have the same E-geodesics.
b) BE(X, X) = 0 for all X 
 (E).
(E).
c) SE = 0.
d) BE = AE.
COROLLARY 8.6. The restricted connections DE and  are equal if and only if they have the same geodesics and the same restricted torsion tensors.
are equal if and only if they have the same geodesics and the same restricted torsion tensors.
COROLLARY 8.7. Given a restricted connection  , there is a unique restricted connection DE having the same geodesics as
, there is a unique restricted connection DE having the same geodesics as  and zero restricted torsion.
and zero restricted torsion.
PROOF. The results on (Hicks 1965, section 5.4) follow ipsis literis in the restricted context. For instance, we show the latter. The uniqueness results from the second proposition. To show the existence, we define

(8.11)
DE is clearly an E-connection. We compute
BE(X, Y) =  T(X, Y) = AE , SE = 0,
T(X, Y) = AE , SE = 0,
since the torsion is skew symmetric. Since SE = 0, they have the same geodesics. Finally, a simple calculation gives
TE =  - 2AE = 0
- 2AE = 0
so DE has zero torsion. 
In terms of the original full connection, there is still too much liberty. We can extend DE to a full connection with arbitrary completions DF, E, DTM, F. In the spirit of Cartan's approach, one would like to characterize special completions. We plan to pursue this futurely. For this purpose, Vilms (1967) and Vagner (1965) can provide the starting point.
ACKNOWLEDGEMENTS
Supported in part by fellowships from FAPERJ and CNPq/PCI. We thank Prof. Manfredo do Carmo for encouragement and many stories about Cartan.
RESUMO
Nesta nota revisitamos a comunicação de E. Cartan no Congresso Internacional da IMU em Bolonha, Itália. As distribuições aqui consideradas serão do mesmo tipo que as tomadas por Cartan, uma classe especial que chamamos fortemente não-holônomas. Porém, preparamos o caminho para a aplicação do método da equivalência de Cartan (uma ferramenta poderosa para a obtenção de invariantes) a distribuições mais gerais.
Palavras-chave: mecânica não holonômica, método de equivalência de Cartan, conexões afins.
MONTGOMERY R. 2001. A tour of subriemannian geometries: geodesics and applications, American Mathematical Society, to appear.
Correspondence to: Jair Koiller
E-mail: jair@lncc.br
- ARNOLD V. 1978. Mathematical Methods in Classical Mechanics, Springer-Verlag.
- ARNOL'D V, KOZLOV V AND NEISHTADT A. 1988. Dynamical Systems III, Springer-Verlag.
- BATES L AND CUSHMAN R. 1999. What is a completely integrable nonholonomic dynamical system? Rep Math Phys, 44(1/2): 29-35.
- BLAJER W. 1995. An orthonormal tangent space method for constrained multibody systems, Comput Methods Appl Mech Engrg, 121: 45-57.
- BRYANT RL, CHERN SS, GARDNER RB, GOLDSCHMIDT HL AND GRIFFITS PA. 1991. Exterior Differential Systems, Springer-Verlag.
- CARTAN E. 1928. Sur la represéntation géométrique des systčmes matériels non holonomes, Proc Int Congr Math, Bologna, 4: 253-261.
- CARTAN E. 1939. Selecta, Gauthier-Villars; 1910, Ann Sci École Norm Sup, 27: 109-192.
- CHOQUET-BRUHAT Y, DEWITT-MORETTE C AND DILLARD-BLEICK M. 1997. Analysis, Manifolds and Physics, North-Holland.
- CUSHMAN R AND NIATYCKI J. 1998. Proceedings of the Pacific Institute of Mathematical Sciences workshop on nonholonomic constraints in dynamics, Rep Mathl Physics, 42: 1/2.
- DE LEÓN M AND MARTIN DE DIEGO D. 1996. On the geometry of non-holonomic Lagrangian systems, J Math Phys, 37: 3389-3414.
- GARDNER R. 1989. The Method of Equivalence and its Applications, SIAM.
- HICKS NJ. 1965. Notes on Differential Geometry, Van Nostrand.
- KOILLER J. 1992. Reduction of some classical non-holonomic systems with symmetry, Arch Rational Mech Anal, 118: 113-148.
- KOSCHORKE U. 1981. Vector fields and other vector bundle morphisms-a singularity approach. Lecture Notes in Mathematics 847, Springer, Berlin.
- KRISHNAPRASAD PS, BLOCH A, MARSDEN JE AND MURRAY RM. 1996. Non-holonomic Mechanics and Symmetry, Arch Ratl Mech Analysis, 136 (1): 21-99.
- LI Z AND CANNY JF. 1993. Non-holonomic Motion Planning, Kluwer.
- MILNOR J AND STASHEFF JD. 1974. Characteristic classes, Princeton Univ. Press.
- POSTNIKOV A, SHAPIRO B AND SHAPIRO M. 1999. Algebras of curvature forms on homogeneous manifolds. In: Differential topology, infinite-dimensional Lie algebras, and applications, 227-235, Amer Math Soc Transl Ser 2, 194, Amer Math Soc, Providence, RI.
- VAGNER VV. 1965. Geometria del calcolo delle variazioni, Ed. Cremonese.
- VERSHIK AM AND GERSHKOVICH V. 1994. Nonholonomic dynamical systems, geometry of distributions and variational problems, in V.I. ARNOLD, S.P. NOVIKOV (Eds.), Dynamical Systems VII, Springer-Verlag.
- VILMS J. 1967. Connections on tangent bundles, J Diff Geometry 1: 235-243.
Publication Dates
-
Publication in this collection
08 June 2001 -
Date of issue
June 2001
History
-
Accepted
12 Feb 2001 -
Received
05 Feb 2001