Integral energy spectra of hadrons induced by one-single nucleon by the method of characteristics

REGULAR ARTICLES

Integral energy spectra of hadrons induced by one-single nucleon by the method of characteristics

K. H. Tsui^I; H. M. Portella^I; A. S. Gomes^I; H. Shigueoka^I; L. C. S. de Oliveira^II

^IInstituto de Física - Universidade Federal Fluminense, Campus da Praia Vermelha, Av. General Milton Tavares de Souza s/n, Gragoatá, 24.210-340, Niterói, RJ, Brazil

^IICentro Brasileiro de Pesquisas Físicas CBPF/MCT, Rua Dr. Xavier Sigaud 150, 22290-180, Rio de Janeiro, RJ, Brazil

ABSTRACT

Hadron energy spectra induced by one-single nucleon are obtained solving diffusion equations by the method of characteristics. Our solutions are a generalization of earlier papers that allow us to calculate hadron fluxes including the energy dependence of the interaction lengths and inelasticities. A comparison with the integral hadron spectra of the so-called ''halo events" detected by the Brazil-Japan Collaboration at Mt. Chacaltaya is made, in order to test our solutions. A reasonable agreement between then is obtained, considering the rising with energy of the nucleon inelasticity coefficient.

Keywords: Cosmic Rays; Hadron energy spectra; Method of characteristics; Halo events

I. INTRODUCTION

In the last year, we developed an analytical method [1] that allow us to calculate with a good precision the hadronic and electromagnetic components of cosmic rays in the earth's atmosphere. Our solutions, obtained with a power law primary spectra, permit us to include the scaling violation for the hadron interactions and the energy dependence of the hadron interaction mean-free paths and inelasticities.

For sake of completeness, we looked for another boundary condition in order to test our analytical method. If we choose, for instance, a single nucleon (delta function) as the boundary condition, the nucleon spectra then obtained is an exact solution. They are presented in the usual modified Bessel functions of order 1. Differently of the common solutions found in the literature [2-4], the argument of these functions is variable according to the index of summation. This is a consequence of the energy dependence of the interaction mean-free path and inelasticity. This initial condition is important to describe the flux of the so-called "halo events" detected with nuclear emulsion at mountain altitudes and Extensive Air Showers as well.

The Brazil-Japan Collaboration has detected cosmic-ray events in the energy range (10¹³ - 10¹⁷) eV with emulsion chamber exposed at Mt. Chacaltaya. About 20 events have been observed in the visible energy region E > 1000 TeV. Approximately, half of them [5-8] are associated with an uniform darkened wide area on X-ray films. This area, in the central part, is called "halo" and so these events are called "halo events". Similar experiments at Pamir [9],Fuji [10] and Kanbala [11] have also observed such events. Recently, a new experiment [12], using a hadron calorimeter associated with emulsion chambers at Mt. Chacaltaya, has reported this kind of events too. Thus, the appearance of a strong concentration of energy and particles as a halo seems to be a common feature in this energy region.

After the eighties, these super-families were also compared with simulated ones using different primary compositions and models for high-energy nuclear interactions [13-15]. These simulations cannot describe fully all events with the same inputs on primary composition and nuclear collision models. Due to their big values of the hadronic number and energy, some authors [16] suggested that these events can be explained as centauro-like ones.

An important issue in the high energy region concerns to the behavior of the inelasticity, which is defined as the fraction of energy giving up by the leading hadron in a collision induced by an incident hadron on a target nucleon or nucleus. This parameter has been exhaustively studied in several papers, but until now continues to be an open question. Several authors have suggested that the average inelasticity coefficient is an increasing function of the energy [17,18], whereas others proposed that it is a decreasing one [19-21]. However, high energy cosmic rays, which reflects the nuclear interaction in the energy region covering 1 to 100 TeV, are well fitted with a constant value of the mean inelasticity equal to 0.50 [22,23]. At higher energies, in which these super-families belong, a constant value for the inelasticity is no longer valid in order to explain experimental data. This is why, we think that our method is important to clarify this particular aspect.

This paper is organized as follows: In section II we obtain the integral hadron energy spectra. The nucleon spectra, in real space, is evaluated for the method of residues arriving to an exact solution. For the meson case, we use a parametrization made by Portella [24] that relates the charged pion-to-nucleon ratio at mountain altitudes. In section III we compare these fluxes with the data of some halo events (P06, Ursa Maior, Andromeda and Mini-Andromeda III) [6-8]. In section IV we discuss the results and make some remarks and conclusions.

II. THE HADRON ENERGY SPECTRA

As described in the ^{Appendix B}, the Eq(B.5) represents the Mellin transform of the nucleon flux.

Considering the single incident nucleon with energy E₀ as,

so the Mellin transform of this initial condition is

By inverting the above Mellin transform, we obtain the nucleon flux in a formal way that reads

The only contribution to the flux comes from the essential pole s = s₀ in A(s). To consider this residue, we expand the exponential function in power series to obtain

To evaluate the residue, we define the function acting on the (s - s₀) powers inside the integral by G(s) = = g^s. Since G(s) is analytic in the neighborhood of s = s₀, we expand it in a Laurent series about s = s₀ so that Res(s₀) becomes

By taking (n-m) = +1 terms, we pick up the contributions to the essential residue so that

where Z²(n)/4 = (A/B)^b ( t/l_N)(1/d)(lng). The last equation can be rewritten in terms of the modified Bessel functions of order 1. Thus, results as

This is semi-divergent. It diverges up to some nth term due to the factors like ()ⁿ. Afterwards, it begins to converge due to the factorials of n. We notice that, with the energy dependence, g = g(n) is a function of the summation index n, so that Z(n) is a function of n through lng. For the single incident nucleon case, the fraction < 1 so that g is larger than unity and lng is positive. Consequently, Z²(n) is positive which leads to the modified Bessel function solution. With k = 0, g = is only a function of E, and lng is then independent of n.

The essential residue here plays a very important role because it represents the flux at a given atmospheric depth . We remark that this case of single incident nucleon can also be solved in real space in terms of probability distributions under the assumption of constant mean-free path and uniform elasticity [2,3]. In the Mellin transform space, it can also be solved by residues under the same assumption [4]. In both approaches, the results are in terms of the modified Bessel functions I₁(Z) of order 1. Here, we have generalized the earlier works [2,3] to the case of energy dependent mean-free path and elasticity. In this case, the argument of the modified Bessel function is now n-dependent, Z = Z(n).

The pion fluxes at mountain altitudes are obtained from nucleon intensities using a parametrization taken from[24] and written as

where a = 0.43 and b = 0.04 TeV^-1 for Mt. Chacaltaya. The integral flux of hadrons is then easily calculated from Eq. (7) and the equation above. It can be written as follows

The integral energy spectrum of hadrons for halo events is presented in the fractional form, that is

The hadronic visible energy is the energy of hadrons detected by means of electromagnetic showers induced by g-rays from p⁰ decays. It is related to the hadron energy as

We used for k _g (gamma ray inelasticity) the mean value 0.25 [10].

III. NUMERICAL RESULTS

In order to make numerical calculations about the integral hadron fluxes, we take into account the nucleon collision mean-free path in the earth's atmosphere decreasing with the energy. We have used the expression l_N(E) = l_N()^-b with B = 1 TeV, l_N = 83 g/cm² and b = 0.056 which are obtained from accelerator and EAS data in the region 1 TeV < E_lab < 1000 TeV [25]. For the pion mean-free path, we assume that l _p / l_N 1.4, and that it has the same energy dependence like the nucleon case [32]. In the present calculation we have only one free parameter, A(TeV), which is the normalization factor of the energy in Mellin's transform.

Figure 1 below shows a comparison of our integral hadron fluxes with the data of four halo events detected at Mt. Chacaltaya by the Brazil-Japan Collaboration. In this figure two lines appear representing the inelasticity coefficients, rising (dotted) and decreasing (dashed) with energy. Our calculations are obtained with 0.53 < K_N < 0.64 and 0.53 > K_N > 0.38 for dotted and dashed lines, respectively. We notice that the solution with inelasticity coefficient rising with energy is the best one, confirming recent results about ordinary families originated from power law spectrum measured at mountain altitudes [1,33].

IV. DISCUSSIONS AND CONCLUSIONS

Using a recently method developed by us, we calculated the nucleon flux at different depths in a wide energy range started by one single nucleon. We have generalized earlier papers which did not include the energy dependence of the collision mean-free path and of the mean nucleon inelasticity. Our solution is presented in the usual modified Bessel functions of order 1. In our solution, the argument of those functions is variable according the summation index differently of the common solution found in the literature. This fact is related directly with the energy dependence of the two parameters mentioned above.

The meson fluxes are obtained with a parametrization already mentioned in the text. A comparison with the integral hadronic spectra measured at Mt. Chacaltaya for 4 halo events is made. A best fit is obtained for < K_N > rising with energy in the range 2 < < 1000 TeV. The above parametrization is calculated considering a breaking of scaling law in the fragmentation region only.

The effect of the energy variation of the interaction mean-free path on the integral hadron flux was also worked out. When the energy increases the collision mean-free path decreases, and the number of produced hadrons is enhanced because the inelastic cross section becomes higher, nevertheless these hadrons are in a lower energy range. Therefore, these particles are out of the detector's threshold resulting in a steeper flux. The same effect appears in the discussion of the inelasticity coefficient. When the inelasticity rises with energy the number of produced particles becomes higher. Therefore, particles in the high energy range are in lower number compared with the cases of the coefficient of inelasticity constant or decreasing with energy.

Acknowledgments

This work was supported by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq, The Brazilian National Council of Scientific and Technological Developments) and the Fundacão de Amparo a Pesquisa do Estado do Rio de Janeiro (FAPERJ, The Research Fostering Foundation of the State of Rio de Janeiro).

[1] K. H. Tsui et al, J. Phys. G: Nucl. and Part. Phys. 31, 1275 (2005).

[2] N. Arata and F. M. O. Castro, Braz. J. Phys. 18, 261 (1988).

[3] N. G. Boyadzhyan, A. P. Garayaka, and E A Mamidzhanyan, Sov. J. Nucl. Phys. 34, 67 (1981).

[4] J. Bellandi Filho et al, J. Phys. G: Nucl. Part. Phys. 18, 1559 (1992).

[5] C. M. G. Lattes et al, ICRC 7, 2275 (1971).

[6] N. M. Amato, N. Arata, and R. H. C. Maldonado, Il Nuovo Cimento 10C, 559 (1987).

[7] J. A. Chinellato, PhD Thesis University of Campinas, Brazil (1981).

[8] S. Yamashita, J. Phys. Soc. Japan 54, 529 (1985).

[9] Pamir Collab., Proc. of the 20th ICRC 5, 383 (1987).

[10] M. Akashi et al, Il Nuovo Cimento 67A, 221 (1982).

[11] J. R. Ren et al, Proc. of the 20th ICRC 5, 375 (1987).

[12] H. Aoki et al, J. Phys. G: Nucl. and Part. Phys. 30, 137 (2004).

[13] L. N. Capedevielle et al, KFK Report 4998 (1992).

[14] N. N. Kalmikov and S. S. Ostapchenko, Yad. Fiz. 56, 105 (1993).

[15] K. Werner, Phys. Rep. 232, 87 (1993).

[16] N. M. Amato et al, J. Phys. G: Nucl. and Part. Phys. 20, 829 (1994).

[17] J. D. Deus, Phys. Rev. D 32, 2334 (1985).

[18] A. B. Kaidalov and K. A. Ter-Martyrosian, Phys. Lett. B 117, 247 (1982). A. B. Kaidalov and K. A. Ter-Martyrosian, Sov. J. Nucl. Phys. 40, 135R (1984).

[19] G N Fowler et al, Phys. Rev. D 35, 870 (1987). G N Fowler et al, Phys. Rev. C 40, 1219R (1989).

[20] A. Ohsawa and K. Sawayanagi, Phys. Rev. D 45, 3128 (1992).

[21] Z. Wlodarczyk et al, J. Phys. G: Nucl. and Part. Phys. 21, 281 (1995).

[22] C. R. A. Augusto et al, Phys. Rev. D 61, 012003 (1999).

[23] A. Ohsawa, Prog. Theor. Phys. 92, 1005 (1994).

[24] H. M. Portella, PhD Thesis - CBPF, Brazil, , 94 (1999).

[25] H. M. Portella, F. M. O. Castro, and N. Arata, J. Phys. G: Nucl. and Part. Phys. 14, 1157 (1988).

[26] H. M. Portella, H. Shigueoka, A. S. Gomes, and C. E. C. Lima, J. Phys. G: Nucl. and Part. Phys. 27, 191 (2001).

[27] J. Bellandi Filho et al, Prog. Theor. Phys. 83, 58 (1990).

[28] R. Courrant and D. Hilbert, Methods of Mathematical Physics, Vol. II, Chapter II (Interscience, New York ) (1962).

[29] K. H. Tsui, Optics Commun. 90, 283 (1992).

[30] K. H. Tsui, Phys. Fluids B 5, 3808 (1993).

[31] L. Landau and G. Rumer, Proc. R. Soc. 166A, 213 (1938).

[32] H. M. Portella et al, J. Phys. A 31, 6861 (1998).

[33] H. M. Portella, L. C. S. Oliveira, and C. E. C. Lima, Int. J. Mod. Phys. A 19, 3583 (2004).

Received on 12 December, 2006

Appendix A. Method of characteristics for nucleon diffusion equations

From considerations of different fundamental physical processes, the number density flux of nucleons N(E,t) per energy interval dE centered at energy E at a given atmospheric depth t is described by

where l(E) is the energy dependent mean-free path, h(E^') = E/E^' < 1 is the elasticity, u(h) is the elasticity distribution. Modelling the mean-free path by a power index b [25],

Eq. (1) reads

where B is the normalization energy of the mean-free path. Instead of introducing mapping operators to the two terms on the right side of Eq. (A.3) to solve it formally in real space [26], we proceed to use the Mellin transform defined by

where the energy E is normalized to some reference energy A, so that the transform does not carry dimension of energy to power s. Now, Eq. (A.3) in the transform space reads

With K as the normalization energy of elasticity, we use the following average model of elasticity [20] to power s

where s₀ = -1/d. For a uniform elasticity distribution, we have k = 0, d = 1, and s₀ = -1. In particular, taking s = 1 gives the average elasticity

The equation of the flux transform then becomes

We notice that, if the energy E in the Mellin transform was not normalized to some reference energy A, then 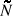(s,t), 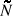(s+b,t) and 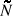(s+b+ks,t) would have different dimensions in energy which would conceal the effects of the energy dependence in mean-free path and elasticity. Here, in Eq. (A.6), they have the same dimension of N(E,0). The mean-free path factor (A/B)^b and the elasticity factor (A/K)^{k s} are working as the weighting factors among different transforms.

We observe that the nucleon cascade equation, Eq. (A.1), has two competing terms on the right side. The first term is the diffusion term that drains the flux N(E,t) dE at E to lower energies E^'. The second term is the attenuation term that fills the flux at E by higher energies E^'. Since the mean-free path scaled by Eq. (A.2) vanishes as E/B goes to infinity with b > 0, the first term would dominate the equation and the spatial gradient of the flux would be very negative at high energies. As for the elasticity h = E/E^' < 1, it goes to zero at a given E as E^' goes to infinity. For the average elasticity < h > of Eq. (A.8) to have the same limit at a given E as E^'/K becomes infinite, k has to be negative.

This partial differential equation is equivalent to the following set of ordinary differential equations which describes the trajectory of the coordinate point (s, t, 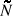) in the functional space parameterized to x [28]

This method of characteristics to solve first order partial differential equations was used in superradiant free electron lasers [29,30]. Solving for the equality between dt and ds,

we get a trajectory between the variables t and s through the parameter x, t = t(s,b, k), which is the characteristics of the partial differential equation, Eq. (B.1). Considering uniform elasticity, k = 0, d = 1, we have

where s(t) > s(0). Following Landau and Rumer [31] in their pioneering and landmark paper of electromagnetic cascade, s in the transform space, in our case here, also bears the meaning of shower age parameter. By recognizing the Mellin transform, with integer s, as also the s th energy moment of the distribution function N(E,t), Landau and Rumer constructed a scheme to uncover many physical properties of the electromagnetic cascade by using functional analysis on 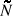(s,t) itself without doing the inverse transform. They noticed that 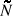(s,t) represented actually real physical parameters when and only when s was an integer.

To get the transform of the flux, we could solve the equality of d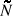 with dx, or with ds, or with dt. Since the boundary condition of 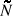is given in terms of s at t = 0 , we choose to solve with dt

where µ(s) = (A/B)^b[1-A(s)]. The factor (A/B)^b in Eqs. (B.4 and B.5) represents the relative weight of the mean-free path to the elasticity effect.

Appendix B.  Method of Characteristics

(

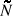To solve Eq. (A.9), we notice that both b and k are much less than s, so that one way to solve this equation is by iterations. Some researchers define two operators in the transform space to represent the two finite difference terms on the right side of Eq. (A.9) to solve it formally by operators [27]. Following the property b, k < s, we choose to make a Taylor expansion of the two terms in 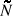(s,t) to get a first order differential equation. For nucleons we have

Publication Dates

• Publication in this collection
  17 July 2007
• Date of issue
  June 2007

History

• Received
  12 Dec 2006