Interaction Between Motions of Robotic Manipulator arms and the Non-Fixed base in On-Orbit Operations

ABSTRACT:

The objective of this paper is to study the problem of the robotic manipulator operating on a non-fixed base by considering two dynamics scenarios. One in which the base is free to react in response to the robotic manipulator motion and the other in which the robotic manipulator moves its links in such a way to compensate the reaction forces on the platform so as to keep it stable. This approach is passive in the sense that no additional control effort has to be done to compensate the effects of the reaction forces on the platform. The methodology to approach the problem includes lab experiments aiming the dynamics analysis of a robotic manipulator operating on an ice platform on a glass table. The mathematical model of a satellite like a robotic manipulator is developed and then implemented in a computer by using the MATLAB software environment. The results of the computer simulations confirm that the control effort for the attitude control is larger for the case in which the links are in operation compared to the case in which the robotic manipulator is not working. For the passive case, the results confirm the attitude stability of the robotic manipulator platform when it is working. The passive case is that in which the robotic manipulator links are moving in a synchronized configuration and in a reverse sense.

KEYWORDS:
On-orbit operations; attitude control robotic manipulators; Non-inertial platform

INTRODUCTION

In this section it is discussed the robot on-orbit applications and some basic concepts regarding excitation of robotic platform in response to on-board robot activities as well as the concepts of robot and telerobot. The platform excitation due to the robotic manipulator activities falls within a wide area of the attitude dynamics and control, known as control structure interaction (CSI).

It is very risky and highly expensive to send humans into space missions for any kind of activity. Presently, there is a consensus towards replacing humans by space robots in the space activities. Robots are machines that can be replaced and improved thanks to the enormous advances of the information technology (IT). Robots represent an attractive option to replace humans in space. Operations that require robots are on-orbit rendezvous and docking/berthing (RVD/B) of spacecraft (NASA 2005, Kawano et al. 1989, 1994, 1998, 2001; Mokuno et al. 1995), assembling of space vehicle in space (as done when assembling the International Space Station - ISS), on-orbit servicing, OOS (Skaar and Ruoff 1994), for maintenances and assistances, scientific experiments in space, missions for planetary explorations, among others. This is the direction of the future of the space exploration: to use intelligent robots and systems of robots with capability of local decision taking without the need for ground station commands/decision taking. There are some important differences between the ground-based and space-based robotic manipulators dynamics. The ground-based robotic manipulators may work on fixed platforms in the Earth gravitational environment. On the other hand space-based robotic manipulators work on movable and apparently weightless platforms in microgravity environments. The ground-based robotic manipulator platform may not move in response to the motion of the robotic manipulators as they are fixed while they execute required tasks. The on-orbit environment is characterized by microgravity and, because of this, the robotic manipulator base is not fixed in space (in inertial sense). It is free to move in response to the motion of the robotic manipulator when it is in activity.

On-orbit activities (Pedersen et al. 2004) may be external to the space vehicle (extravehicular activities - EVA) or internal to the spacecraft. Other space activities refer to towing a satellite from one orbit to another or simply docking with a spacecraft aiming maintenance operations. The scenario for an on-orbit operation may be as that of one robotic manipulator docked or berthed in a spacecraft and working on it. Depending on the work to be executed, the spacecraft becomes the robotic manipulator base and it may move in response to the manipulator links motion while it performs tasks. In such scenario the attitude and the translational motion of the spacecraft may be disturbed, requiring attitude and orbit control.

A telerobot differs from the autonomous robot because it involves a human located on a central control station to command the robot. The nowadays tendency to use autonomous robots requires more security to assure the success of on-orbit operations. The success of missions may be achieved by minimizing collision risks in the robot space work, by controlling the robot's hand applied forces, preventing malfunctioning of the hardware and software through risk analysis, as well as dynamical analysis to detection/prevention, and controlling the robotic manipulator platform excitation due the robotic operations. To close the discussion about this problem, it can be stated that the study of the response of the non-inertial platforms to the robot motions is fundamental for the success of all the space operations to be taken in the microgravity environment. One of the main requirements from the control area is to maintain the robotic platform stable when on-board robots are working. The platform may be the robotic base if the space vehicle is a spacecraft like robotic manipulator or a spacecraft that carries a robotic manipulator on its structure. So it is necessary to have an on-board control subsystem to control the excitation on the platform due to reaction torque and force arising from the robot activities. Such control may be attitude control and/or orbit control so as to maintain the spacecraft stable while the robotic manipulator operates. This can be done by using active control to keep the platform stable. The active control requires sensors and actuators. The sensors detect the platform positions and rates. The sensor data are read and processed by the attitude and orbit control subsystem (AOCS) software (SW). Then appropriate designed controllers command the actuators to act and keep the platform stable. This paper presents a robotic manipulator with the links planned to move in a synchronized way but in reverse sense. The idea is to eliminate the reaction torque on the robotic platform and then reduce the control effort to make the spacecraft stable during the manipulator activity.

LITERATURE REVIEW

A wide space robotics literature review is out of the scope of this paper. However some studies related to CSI for satellite and space stations are presented next. Space vehicles comprising robotic manipulator for on-orbit servicing and spacecraft like robotic manipulators fall within the CSI field.

Da Fonseca (1998) presented the modeling and dynamics analysis including attitude and vibration control for a space station containing a large flexible robotic manipulator with capability to move non-negligible masses. In the research the finite element technique is combined with the Lagrangian formulation to obtain the system equations of the dynamics. The linear quadratic regulator (LQR) technique was used to control the rotational-vibrational motion of the station. The control effort taking into account the impact of the elastic flexibility of the manipulator links on the attitude motion of the complete system is presented and discussed in that study. Arantes Jr. (2011) studied the RVD for non-cooperative targets. The author used pose (position and orientation) and motion estimation as well as dual quaternion to obtain the relative attitude motion. The chaser spacecraft was assumed to be like an autonomous space robot. The on-board estimation of the target and chaser relative attitude and relative position were the key aspects to synchronize the relative attitude aiming a close proximity of the target without collision. In the same line there is the research from Goddard Jr (1997), in which the author uses the extended Kalman filtering for pose and motion estimation. Longman (1994) presents a tutorial overview of the dynamics and control of satellite-mounted robots. The author discusses the problem of robots mounted on a non-fixed base and the satellite motion in response to the robot motion. The article presents the following example to illustrate the problem. The remote manipulator system (RMS), mounted on a Space Shuttle of mass equal to 67,000 kg is to manipulate a 30,000 kg load. By commanding the RMS to move the load 6 m, it results in a relative distance from the Shuttle of 6 m. However, due to opposite motion of the Shuttle of about 1.8 m, it results in a net distance of only 4.2 m with respect to the place the load should be moved to. The author also discusses the problem of attitude perturbation and accelerations related to the robot manipulation of non-negligible masses and the impact of those perturbations in on-board experiments related to microgravity. The tutorial approaches the problem of predicting and correcting the attitude disturbances induced by the robot motion as well as the conditions in which it is required to turn off the attitude control subsystem during the robot operation. The paper belongs to the CSI area. Mukherjee and Zurowski (1994) present techniques of moving appendages for reorientation of free-flying multibody structure. The study belongs also to the CSI area. Alexander and Cannon (1987) discussed and demonstrated experimentally the computation of joint torques for manipulator endpoint control assuming that thrust forces of the vehicle were known. Vafa and Dubowsky (1987) proposed a novel concept (the virtual manipulator) to simplify the kinematics and the dynamics of space robot systems. The virtual concept refers to an imaginary manipulator which is similar to the real one, except by the fact that it is fixed at the center of mass of the complete system. By deriving the motion of the virtual manipulator for a given end effector motion, the motion of the actual system can be obtained in a straightforward manner. Umetani and Yoshida (1987) proposed a technique to control continuously the end effector without actively controlling the vehicle thrust forces. In the article the conservation of momentum for linear and angular motion is used as constraints equations to eliminate the dependent variables and obtain a generalized Jacobian matrix relating the end effector motion to the joint motion. Yoshida (2009) presents achievements in space robotics and states that the dynamic coupling between manipulator reaction and satellite attitude is an important issue. According to his results two approaches were tested. One is the coordinated control in which manipulator reaction is feedforwarded to the attitude control system (feedforward control). The other is the reactionless manipulation in which the manipulator arm moves on a specific path of no reaction onto the base. Both methods were successfully demonstrated. In our paper we use the synchronized reverse motion to obtain such result. Qureshi and Terzopoulos (2008) address the subject of capturing debris autonomously by using a robot. The technique presented in the paper is computer vision, intelligent perception, and control for space robotics. Dubowsky and Papadopoulos (1993) presented the kinematics, dynamics, and control of free-flying and freefloating space robotic systems. The problem of disturbance caused by the robot motion is also addressed in the paper. The authors present and discuss applications that were later implemented in ISS. The free-flying and intelligent spheres are being tested in ISS, and the idea is to use the free-flying systems for inspection of the ISS structure.

MATHEMATICAL MODELING

The methodology used to accomplish this work includes the mathematical modeling of a satellite like robotic manipulator, a lab experiment, and computer simulations by using the MATLAB environment for the sake of dynamical analysis. The methodology includes also the LQR technique to implement the spacecraft attitude control.

In addition to the computer simulations of the mathematical model, a lab experiment has been conducted in the Space Robotics Laboratory (SRL) of the Instituto Tecnológico de Aeronáutica, Departamento de Mecatrônica, Divisao de Mecânica Aeronáutica, aiming the dynamics analysis of a robotic manipulator operating on an ice platform on a glass table. The ice reduces the friction to low level allowing the analysis of the reactions on the platform.

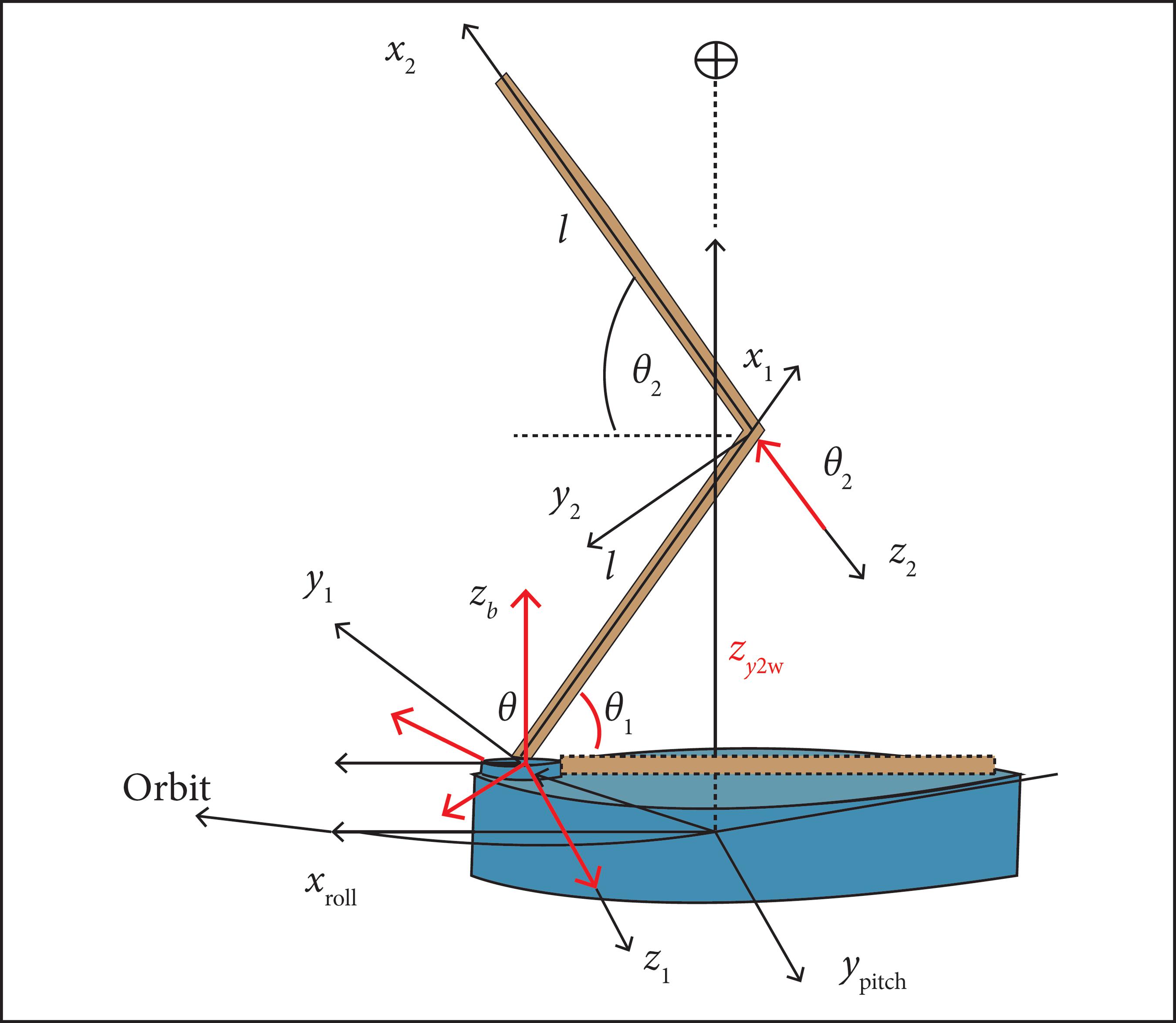
A mathematical model was developed aiming the computer simulations by using the MATLAB SW environment for the sake of dynamical analysis. The simulations aim the active attitude control including analysis of the control effort for two cases, one in which the robotic manipulator is not in operation and the other when the manipulator is operating. The third scenario is for a specific configuration of the robot manipulator in which the links are deployed in opposite directions canceling the associated reactions on the platform. This case shows that an appropriated design of the arms deployment can cancel the reactions on the platform, that is, the arm deployments do not affect the stabilized attitude, except for the rotational motion of the arms. Figure 1 illustrates the physical model of a satellite like a robotic manipulator. The mathematical model is given by Eqs. 3 to 7. These equations of motion have been derived by the Lagrangian formulation for quasi-coordinates (Meirovitch 1970).

Figure 1
Physical model to represent a spacecraft containing a robotic manipulator on its structure.

In Fig. 1, x, y, and z are the roll, pitch, and yaw axes, respectively; x_i, y_i, and z_i (i = 1, 2) are the robotic manipulators' arms axis; q_i (i = 1, 2) are the degrees-of-freedom (DOFs) of the arms; φ_b is the rotational DOF of the manipulator; stands for the Earth; roll, pitch, and yaw are the axes for the attitude representation in the local vertical/local horizontal (LVLH) frame.

For this study only the gravity-gradient torque has been considered as external perturbation. This torque is derived from the gravitational potential energy (for the first order approximation), and the detailed derivation can be seen in Kaplan (1976). The Lagrangian formulation for quasi-coordinates yields the Euler's modified equations including the coupling of the spacecraft rotational motion with the arms motion. The Lagrange's formula for generalized coordinates yields the robotic manipulator equations of motion. The Lagrange's formula for quasi-coordinates is:

(1) $\frac{d}{\mathrm{dt}}\left\{\frac{\mathit{\partial }T}{\mathit{\partial }\mathit{\omega }}\right\}\mathit{+}\left[\tilde{\mathit{\omega }}\right]\left\{\frac{\mathit{\partial }T}{\mathit{\partial }\mathit{\omega }}\right\}\mathit{=}\left\{{\mathit{\tau }}_g\right\}\mathit{+}\left\{{\mathit{\tau }}_c\right\}$

where:

T is the kinetic energy; {τ_g} are {τ_c} the external and the control torque vectors, respectively. yields the angular momentum vector; [ῶ] is a skew symmetric matrix in the components of the angular velocity vector (ω);

For the generalized coordinates, the Lagrange's formula is:

(2) $\frac{d}{\mathrm{dt}}\left(\frac{\mathit{\partial }L}{\mathit{\partial }{\dot{\mathit{\theta }}}_i}\right)\mathit{-}\frac{\mathit{\partial }L}{\mathit{\partial }{\mathit{\theta }}_i}\mathit{=}{Q}_{\mathit{\theta }i}$

where:

L is the Lagrangian function; q_i (i = 1, 2, 3), q₃ = φ, are the DOFs associated with each link of the robot manipulator; Q_qi are the generalized forces.

The Lagrangian function is given by T-V (kinetic and potential energy, respectively). Eventually, L = T, when no potential energy is considered in the problem. In this paper only the kinetic energy T appears in the Lagrangian formulation.

The kinetic energy for the system is given by:

(3) $\begin{array}{c}T\mathit{=}\frac{1}{2}{\left\{\mathit{\omega }\right\}}^T\left[J_p\right]\left\{\mathit{\omega }\right\}\mathit{+}\frac{1}{2}{{\sum }_{i\mathit{=}1}^3\left\{{\dot{\mathit{\Theta }}}_i\mathit{+}\mathit{\omega }\right\}}^T\hfill \\ \left({\left[{\mathit{\Theta }}_i\right]}^T\left[I_{\mathit{\ell }i}\right]\left[{\mathit{\Theta }}_i\right]\right)\left\{{\dot{\mathit{\Theta }}}_i\mathit{+}\mathit{\omega }\right\}\mathit{+}{\left\{\tilde{\mathit{\omega }}\right\}}^T\hfill \\ {\sum }_{i\mathit{=}1}^2\left[I_{\mathit{\ell }i}\right]\left[{\mathit{\Theta }}_i\right]\left\{{\dot{\mathit{\Theta }}}_i\right\}\hfill \end{array}$

where:

[J_p] and [I_li] are the platform inertia matrices associated with the rotational motion (of the complete system) and the arms, respectively; [Θ_i] is the transformation matrix relating the satellite frame (roll, pitch, and yaw axes) to those of the links. [J_T] is function of Θ₁, Θ₂, and Θ₃ (Θ₃ = φ) considering the moments of inertia of the manipulator links, written in the satellite frame. The varying part of the inertia matrix is the second parcel in the right side of Eq. 1. This is to say that as the manipulator links move the total inertia matrix varies.

(4) $\left[J_T\right]\mathit{=}\left[J_p\right]\mathit{+}{\sum }_{i\mathit{=}1}^3{\left[{\mathit{\Theta }}_i\right]}^T\left[l_{\mathit{\ell }i}\right]\left[{\mathit{\Theta }}_i\right]$

It varies with q_i, i = 1, 2, 3. So the matrices [Θ₁], [Θ₂], and [Θ₃] are function of Θ₁, Θ₂, and Θ₃. The third parcel on the right-hand side of the kinetic energy expression represents the crossing terms, and the expression is a function of the satellite and links angular rates, as well as the angles Θ₁, Θ₂, and Θ₃. The coupled terms may be verified in Eqs. 4 to 8.

The kinematics equations considering the linear system (attitude small angles) can be written as (Wie 1998):

(5) $\begin{array}{c}\left\{\begin{array}{c}{\mathit{\omega }}_x\\ {\mathit{\omega }}_y\\ {\mathit{\omega }}_z\end{array}\right\}\mathit{=}\left[\begin{array}{c}1\\ 0\\ 0\end{array}\begin{array}{c}0\\ c\mathit{\phi }\\ \mathit{-}s\mathit{\phi }\end{array}\begin{array}{c}\mathit{-}s\mathit{\theta }\\ s\mathit{\phi }c\mathit{\theta }\\ c\mathit{\phi }c\mathit{\theta }\end{array}\right]\left\{\begin{array}{c}\dot{\mathit{\phi }}\\ \dot{\mathit{\theta }}\\ \dot{\mathit{\psi }}\end{array}\right\}\mathit{-}\hfill \\ \left\{\begin{array}{c}\dot{\mathit{\phi }}\\ \dot{\mathit{\theta }}\\ \dot{\mathit{\psi }}\end{array}\right\}\mathit{-}n\left\{\begin{array}{c}c\mathit{\theta }s\mathit{\psi }\\ s\mathit{\phi }s\mathit{\theta }s\mathit{\psi }\mathit{+}c\mathit{\phi }c\mathit{\psi }\\ c\mathit{\phi }s\mathit{\theta }s\mathit{\psi }\mathit{-}s\mathit{\phi }c\mathit{\psi }\end{array}\right\}\hfill \end{array}$

where:

n is the orbital rate, constant for circular orbit; s and c mean sine and cosine, respectively; Θ, Φ, and Ψ are the pitch, roll, and yaw angles (attitude angles).

The kinematics differential equations for the orbiting spacecraft is then:

(6) $\left\{\begin{array}{c}\dot{\mathit{\phi }}\\ \dot{\mathit{\theta }}\\ \dot{\mathit{\psi }}\end{array}\right\}\mathit{=}\frac{1}{c\mathit{\theta }}\left[\begin{array}{c}c\mathit{\theta }\\ 0\\ 0\end{array}\begin{array}{c}s\mathit{\phi }s\mathit{\theta }\\ c\mathit{\phi }c\mathit{\theta }\\ s\mathit{\phi }\end{array}\begin{array}{c}c\mathit{\phi }s\mathit{\theta }\\ \mathit{-}s\mathit{\phi }c\mathit{\theta }\\ c\mathit{\phi }\end{array}\right]\left\{\begin{array}{c}{\mathit{\omega }}_x\\ {\mathit{\omega }}_y\\ {\mathit{\omega }}_z\end{array}\right\}\mathit{+}\frac{n}{c\mathit{\theta }}\left\{\begin{array}{c}s\mathit{\theta }\\ c\mathit{\psi }c\mathit{\theta }\\ s\mathit{\psi }s\mathit{\theta }\end{array}\right\}$

The Euler modified equations of motion are given by Eq. 1 and can be written as:

(7) $\begin{array}{c}{J}_{\mathrm{tx}}{\dot{\mathit{\omega }}}_x\mathit{-}{I}_{\mathrm{xz}12}{\dot{\mathit{\omega }}}_z\mathit{+}\left(J_{\mathrm{zt}}\mathit{-}{J}_{\mathrm{yt}}\right){\mathit{\omega }}_y\left({\mathit{\omega }}_z\mathit{+}\dot{\mathit{\varphi }}\right)\mathit{+}\hfill \\ \left[I_{y1}s\left(2{\mathit{\theta }}_1\right){\dot{\mathit{\theta }}}_1\mathit{+}{I}_{y2}s\left(2{\mathit{\theta }}_2\right){\dot{\mathit{\theta }}}_2\right]{\mathit{\omega }}_x\mathit{+}\mathrm{\{[}\left[{2I}_{y2}c\left(2{\mathit{\theta }}_2\right)\mathit{+}{I}_{z2}\right]\hfill \\ \left({\dot{\mathit{\theta }}}_2\mathit{-}{\dot{\mathit{\theta }}}_1\right)\mathit{-}{2I}_{y1}c\left(2{\mathit{\theta }}_1\right)\mathit{+}{I}_{z1}]{\dot{\mathit{\theta }}}_1\}\left({\mathit{\omega }}_z\mathit{+}\dot{\mathit{\varphi }}\right)\mathit{-}\hfill \\ I_{xz12}{\mathit{\omega }}_x{\mathit{\omega }}_y\mathit{=}{\mathit{\tau }}_x\mathit{+}{\mathit{\tau }}_{m12}\mathit{-}u\mathit{\varphi }\hfill \end{array}$

(8) $\begin{array}{c}{J}_{\mathrm{yt}}{\dot{\mathit{\omega }}}_y\mathit{+}\left(J_{\mathrm{zt}}\mathit{-}{J}_{\mathrm{xt}}\right){\mathit{\omega }}_x\left({\mathit{\omega }}_z\mathit{+}\dot{\mathit{\varphi }}\right)\mathit{+}\hfill \\ I_{xz1}\left({\left({\mathit{\omega }}_z\mathit{+}\dot{\mathit{\varphi }}\right)}^2\mathit{-}\mathit{\omega }_x{}^2\right)\mathit{=}{\mathit{\tau }}_y\mathit{+}{u}_{\mathit{\theta }1}\mathit{+}{u}_{\mathit{\theta }2}\hfill \end{array}$

(9) $\begin{array}{c}{\mathit{J}}_{{\mathit{z}}_{\mathit{t}}}{\dot{\mathit{\omega }}}_{\mathit{z}}-{\mathit{I}}_{{\mathit{xz}}_{12}}{\dot{\mathit{\omega }}}_{\mathit{x}}+\left({\mathit{J}}_{{\mathit{y}}_{\mathit{t}}}-{\mathit{J}}_{{\mathit{x}}_{\mathit{t}}}\right){\mathit{\omega }}_{\mathit{x}}{\mathit{\omega }}_{\mathit{y}}-[{\mathit{I}}_{{\mathit{y}}_1}\mathit{S}\left(2{\mathit{\theta }}_1\right){\dot{\mathit{\theta }}}_1+\hfill \\ {\mathit{I}}_{{\mathit{y}}_2}\mathit{S}\left(2{\mathit{\theta }}_2\right){\dot{\mathit{\theta }}}_2]{\mathit{\omega }}_{\mathit{x}}+\mathrm{\{[}\left[2{\mathit{I}}_{{\mathit{y}}_2}\mathit{c}\left(2{\mathit{\theta }}_2\right)+{\mathit{I}}_{{\mathit{z}}_2}\right]\left({\dot{\mathit{\theta }}}_2-{\dot{\mathit{\theta }}}_1\right)-\hfill \\ 2{\mathit{I}}_{{\mathit{y}}_1}\mathit{c}\left(2{\mathit{\theta }}_1\right)+{\mathit{I}}_{{\mathit{z}}_1}]{\dot{\mathit{\theta }}}_1\}\left({\mathit{\omega }}_{\mathit{z}}+\dot{\varphi }\right)-{\mathit{I}}_{{\mathit{xz}}_{12}}{\mathit{\omega }}_{\mathit{y}}\left({\mathit{\omega }}_{\mathit{z}}+\dot{\varphi }\right)=\hfill \\ {\mathit{\tau }}_{\mathit{z}}-{\mathit{\tau }}_{{\mathit{xz}}_{12}}+{\mathit{u}}_{\varphi }\hfill \end{array}$

(10) $\begin{array}{c}{\mathit{I}}_{{\mathit{z}}_{12}}\left({\ddot{\mathit{\theta }}}_1+{\dot{\mathit{\omega }}}_{\mathit{y}}\right)+{\mathit{I}}_{{\mathit{z}}_2}\left({\ddot{\mathit{\theta }}}_2-{\ddot{\mathit{\theta }}}_1\right)+\left[{\mathit{I}}_{{\mathit{y}}_1}\mathit{s}2{\mathit{\theta }}_1+{\mathit{I}}_{{\mathit{y}}_2}\mathit{s}2{\mathit{\theta }}_2\right]\hfill \\ \left({\mathit{\omega }}_{\mathit{z}}^2-{\mathit{\omega }}_{\mathit{x}}^2\right)+2\left[{\mathit{I}}_{{\mathit{y}}_1}\mathit{c}2{\mathit{\theta }}_1+{\mathit{I}}_{{\mathit{y}}_2}\mathit{c}2{\mathit{\theta }}_2\right]{\mathit{\omega }}_{\mathit{x}}{\mathit{\omega }}_{\mathit{z}}={\mathit{u}}_{{\mathit{\theta }}_1}\hfill \end{array}$

(11) $\begin{array}{c}{\mathit{I}}_{{\mathit{z}}_2}\left({\ddot{\mathit{\theta }}}_2-{\ddot{\mathit{\theta }}}_1+{\dot{\mathit{\omega }}}_{\mathit{y}}\right)+{\mathit{I}}_{{\mathit{y}}_2}\mathit{s}2{\mathit{\theta }}_2\left({\mathit{\omega }}_{\mathit{z}}^2-{\mathit{\omega }}_{\mathit{x}}^2\right)+\hfill \\ 2{\mathit{I}}_{{\mathit{y}}_2}\mathit{c}2{\mathit{\theta }}_2{\mathit{\omega }}_{\mathit{x}}{\mathit{\omega }}_{\mathit{z}}={\mathit{u}}_{{\mathit{\theta }}_2}\hfill \end{array}$

(12) $\ddot{\varphi }={\mathit{\tau }}_{\varphi }-\frac{{\mathit{J}}_{{\mathit{z}}_{\mathit{t}}}}{{\mathit{I}}_{{\mathit{z}}_1}}{\dot{\mathit{\omega }}}_{\mathit{z}}$

where:

J_tx,J_yt and J_zt are total moments of inertia for the complete system (satellite plus the manipulator). Note that these moments of inertia are not constant for they depend on the manipulator arms position Θ₁ and Θ₂ as well as φ; I_y1, I_y2, I_z1, I_z2 are the arms moments of inertia in their respective axes. The moments of inertia around the links longitudinal axes were neglected; u_Θ1 = I_z12i = 1, 2 are the control torque vector components applied at each joint of the robot links, along z₁ and z₂ axes; is a product of inertia appearing when projecting the moments of inertia of the arms on the satellite axes (function of the angles Θ_i); u_φ = I_zz_b axis). This torque enters into the right side of Eq. 9; τ_m12 is the torque magnitude of the link acting on the platform; φ_b is the angular position of the manipulator rotational joint as shown in Fig. 1. This DOF was not considered in the computer simulation; ω_x, ω_y, and ω_z are the components of the satellite angular velocity vector around the roll, pitch, and yaw axes; ω is function of the attitude angles and rates Φ, Θ, Ψ,Kaplan 1976); τ_x, τ_y, and τ_z are the components of the gravity-gradient torque. For roll, pitch, and yaw, as defined in this study, the gravity-gradient torque vector can be written as (Wie 1998):, ;, , . ( is the torque applied in the base of the robotic manipulator links (rotational joint about

(13) $\left\{{\mathit{\tau }}_{\mathit{g}}\right\}=\left\{\begin{array}{c}3{\mathit{n}}^2\left({\mathit{J}}_{\mathit{tz}}-{\mathit{J}}_{\mathit{ty}}\right)\mathit{s}\mathit{\phi }\mathit{c}\mathit{\phi }{\mathit{c}}^2\mathit{\theta }\hfill \\ 3{\mathit{n}}^2\left({\mathit{J}}_{\mathit{tz}}-{\mathit{J}}_{\mathit{tx}}\right)\mathit{c}\mathit{\phi }\mathit{s}\mathit{\theta }\mathit{c}\mathit{\theta }\hfill \\ 3{\mathit{n}}^2\left({\mathit{J}}_{\mathit{tx}}-{\mathit{J}}_{\mathit{ty}}\right)\mathit{s}\mathit{\phi }\mathit{s}\mathit{\theta }\mathit{c}\mathit{\theta }\hfill \end{array}\right\}$

The linear system equations can be obtained by replacing the linear kinematics equations in the Euler modified equations (Eqs. 7 - 9) and taking the liner terms in Eqs. 10 and 11. The linear kinematics equations are obtained from Eqs. 5 and 6:

(14) $\begin{array}{c}\left\{\begin{array}{c}\dot{\mathit{\phi }}\\ \dot{\mathit{\theta }}\\ \dot{\mathit{\psi }}\end{array}\right\}=\left[\begin{array}{ccc}1& 0& \mathit{\theta }\\ 0& 1& -\mathit{\phi }\\ 0& \mathit{\phi }& 1\end{array}\right]\left\{\begin{array}{c}{\mathit{\omega }}_{\mathit{x}}\\ {\mathit{\omega }}_{\mathit{y}}\\ {\mathit{\omega }}_{\mathit{z}}\end{array}\right\}+\mathit{n}\left\{\begin{array}{c}\mathit{\theta }\\ 1\\ 0\end{array}\right\}\hfill \\ \mathrm{or}\hfill \\ \left\{\begin{array}{c}{\mathit{\omega }}_{\mathit{x}}\\ {\mathit{\omega }}_{\mathit{y}}\\ {\mathit{\omega }}_{\mathit{z}}\end{array}\right\}=\left[\begin{array}{ccc}1& 0& -\mathit{\theta }\\ 0& 1& \mathit{\phi }\\ 0& -\mathit{\phi }& 1\end{array}\right]\left\{\begin{array}{c}\dot{\mathit{\phi }}\\ \dot{\mathit{\theta }}\\ \dot{\mathit{\psi }}\end{array}\right\}-\mathit{n}\left\{\begin{array}{c}\mathit{\psi }\\ 1\\ -\mathit{\phi }\end{array}\right\}\hfill \end{array}$

The linear expression for the gravity-gradient torque is obtained from Eq. 13 as:

(15) $\left\{{\mathit{\tau }}_{\mathit{g}}\right\}=\left\{\begin{array}{c}3{\mathit{n}}^2\left({\mathit{J}}_{\mathit{tz}}-{\mathit{J}}_{\mathit{ty}}\right)\mathit{\phi }\\ 3{\mathit{n}}^2\left({\mathit{J}}_{\mathit{tz}}-{\mathit{J}}_{\mathit{tx}}\right)\mathit{\theta }\\ 0\end{array}\right\}$

This torque appears in the right side of the Euler modified equations (Eqs. 7 - 9). Once the linear system equations are written, the state and the control matrices A and B (see Eq. 16) can be defined.

THE ATTITUDE CONTROL TECHNIQUE

The LQR is used for the spacecraft attitude control. No control is imposed to the robotic manipulator arms. The arms are only commanded to deploy/retract and rotate. The objective is to actively control the spacecraft attitude while the robotic manipulator is operating and then analyze the impact of arms motion on the control effort. Two different versions of mathematical models were used during the simulations. One version in which the deployment/retraction of the arms are not configured to passively cancel the reactions on the platform and the other in which the form of the arms deployment/retraction cancels the reactions on the platform. In such configuration the motion of the arms (when deploying/retracting) does not affect the platform motion. To apply the LQR technique the system equations are linearized about the equilibrium configuration (attitude angles equal to zero). To implement this technique the linear equations are written in the state form as:

(16) $\dot{\mathit{x}}=A\mathit{x}+B\mathit{u}$

where:

x is state vector; u is the state feedback control law resulting from the performance index optimization (cost function). Mathematically the control law is written as:

(17) $\mathit{u}=-K\mathit{x}$

and it minimizes the cost function:

(18) $\mathit{J}=\underset{0}{\overset{\infty }{\int }}{\mathit{x}}^{\mathit{T}}Q\mathit{x}+{\mathit{u}}^{\mathit{T}}R\mathit{u}\mathit{dt}$

where:

K is the gain matrix; the matrices Q and R are arbitrary weight matrices associated with the state and the control input, respectively.

The state vector x is defined as:

(19) $\mathit{x}=\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{\mathit{\theta }}_1\\ {\mathit{\theta }}_2\end{array}\\ \varphi \end{array}\\ \mathit{\theta }\\ \mathit{\phi }\end{array}\\ \begin{array}{c}{\dot{\mathit{\theta }}}_1\\ {\dot{\mathit{\theta }}}_2\\ \begin{array}{c}\dot{\mathit{\psi }}\\ \dot{\mathit{\theta }}\end{array}\end{array}\\ \dot{\mathit{\psi }}\end{array}\right\}=\left\{\begin{array}{c}\begin{array}{c}{\mathit{x}}_1\\ {\mathit{x}}_2\\ {\mathit{x}}_3\\ {\mathit{x}}_4\end{array}\\ {\mathit{x}}_5\\ \begin{array}{c}{\mathit{x}}_6\\ {\mathit{x}}_7\\ {\mathit{x}}_8\end{array}\\ \begin{array}{c}{\mathit{x}}_9\\ {\mathit{x}}_{10}\end{array}\end{array}\right\}$

For the sake of the computer simulation, φ_b (the DOF for the first link of the manipulator - see Fig. 1) was not considered since it plays a role similar to a reaction wheel mounted on the platform and is always under the spacecraft control subsystem. The state matrix is given by:

(20) $A=\left[\begin{array}{c}\mathit{Z}\hfill \\ {\mathit{J}}^{-1}{\mathit{c}}_2\hfill \end{array}\begin{array}{c}\mathit{I}\hfill \\ {\mathit{J}}^{-1}{\mathit{c}}_1\hfill \end{array}\right]$

where:

Z = 5 × 5 null matrix; I = 5 × 5 identity matrix; and

(21) $J\mathit{=}\left[\begin{array}{cccc}{\mathit{I}}_{\mathit{x}}\left({\mathit{\theta }}_{\mathit{i}}\right)& {\mathit{I}}_{{\mathit{z}}_2}& -\mathit{Iyz}\left({\mathit{\theta }}_{\mathit{i}}\right)& -{\mathit{I}}_{\mathit{x}}\left({\mathit{\theta }}_{\mathit{i}}\right)\\ {\mathit{I}}_{{\mathit{z}}_2}& {\mathit{I}}_{\mathit{y}}& 0& -{\mathit{I}}_{{\mathit{z}}_2}\\ 0& 0& {\mathit{J}}_{\mathit{tx}0}+{\mathit{I}}_{\mathit{x}}\left({\mathit{\theta }}_{\mathit{i}}\right)& 0\\ -{\mathit{I}}_{\mathit{x}}\left({\mathit{\theta }}_{\mathit{i}}\right)& -{\mathit{I}}_{{\mathit{z}}_2}& 0& {\mathit{J}}_{\mathit{tx}0}+{\mathit{I}}_{\mathit{y}}\\ 0& 0& -{\mathit{I}}_{\mathit{xz}}\left({\mathit{\theta }}_{\mathit{i}}\right)& 0\end{array}\begin{array}{c}0\\ 0\\ -{\mathit{I}}_{\mathit{xz}}\left({\mathit{\theta }}_{\mathit{i}}\right)\\ 0\\ {\mathit{J}}_{\mathit{tz}0}+{\mathit{I}}_{\mathit{z}}\left({\mathit{\theta }}_{\mathit{i}}\right)\end{array}\right]$

The inertia properties in function of q_i are the moments of inertia of the manipulator links written in the satellite frame.

(22) $C1=\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& -\mathit{n}\left({\mathit{J}}_{\mathit{tx}}-{\mathit{J}}_{\mathit{ty}}+{\mathit{J}}_{\mathit{tz}}\right)\\ 0& 0& 0& 0& 0\\ 0& 0& \mathit{n}\left({\mathit{J}}_{\mathit{tx}}-{\mathit{J}}_{\mathit{ty}}+{\mathit{J}}_{\mathit{tz}}\right)& 0& 0\end{array}\right]$

(23) $C2=\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& -4{\mathit{n}}^2\left({\mathit{J}}_{\mathit{ty}}-{\mathit{J}}_{\mathit{tz}}\right)& 0& 0\\ 0& 0& 0& -3{\mathit{n}}^2({\mathit{J}}_{\mathit{tx}}-{\mathit{J}}_{\mathit{tz}})& 0\\ 0& 0& \mathit{n}\left({\mathit{J}}_{\mathit{tx}}-{\mathit{J}}_{\mathit{ty}}+{\mathit{J}}_{\mathit{tz}}\right)& 0& {\mathit{n}}^2\left({\mathit{J}}_{\mathit{tx}}-{\mathit{J}}_{\mathit{ty}}\right)\end{array}\right]$

In spite of being arbitrary matrices, Q must be a positive semi-definite state matrix and R must be positive definite witting matrix. Matrices A and B are the plant and input matrices. The control input matrices R and Q are arbitrary. The state matrix Q is 10 × 10 and diagonal. All the elements were chosen to equal to 1, except the elements Q(4,4) = Q(9,9) = 1e+4. The input matrix R is 4 × 4, and all the elements are 1e+3, except R(4,4) = 1e-9.

The LQR technique requires the solution of the Riccati algebraic equation given by:

(24) $[\mathit{A}{]}^{\mathit{T}}[\mathit{P}]+[\mathit{P}\mathrm{][}\mathit{A}]+[\mathit{Q}]-[\mathit{P}\mathrm{][}\mathit{B}\mathrm{][}\mathit{R}{]}^{-1}[\mathit{B}{]}^{\mathit{T}}[\mathit{P}]=0$

where:

P is the Riccati matrix.

The plant matrix involves the non-constant inertia matrix (see Eq. 4) and must be solved at each step of integration. The differential equations representing the dynamics of a spacecraft like a robotic manipulator are characterized by an inertia matrix that varies with respect to time. The motion of the arm moves the link masses during the robotic operation, changing the moments and product of inertia of the whole space vehicle. The control technique involves working with an inertia matrix that must be updated at each step of integration. The block diagram shown in Fig. 2 presents this important feature of this research. In Fig. 2, u(t) is the state feedback control, e(t) refers to the error given by ref(t) − x_out (the state output) to provide the error, and t is the time.

Figure 2
Control block diagram.

The output returns to the dynamics model updating the inertia matrix and also to the reference for the evaluation of the error.

LAB EXPERIMENT

The planned experiment infrastructure consists of glass table, two floating robotic manipulators, a laptop, and the Kinect sensor, as shown in Fig. 3.

Figure 3
Glass table, robotic manipulator, a target, Kinect sensor in a bar over the table, and a laptop.

The mathematical model presented in this paper did not consider the DOF of the robotic manipulator grasping hand. An intelligent sensor (Kinect) is planned to track the manipulators motions on the table and is part of a communication subsystem to receive data from the sensor as well as to issue commands to the robot. This communication subsystem consists of a laptop, the Bluetooth technology and Arduinos. The complete system is human-operated and puts the complete system in the category of telerobots. Figures 4, 5, and 6 show the Kinect and the manipulator hardware communication configuration.

Figure 4
Kinect sensor to track the motion of the robotic manipulator on the glass table.

Figure 5
Experiment communication system diagram.

Figure 6
DOFs of the robotic manipulator on the platform.

The Kinect is a device of sensing movements developed by Microsoft® for the Xbox 360 console. It is equipped with a camera system that allows the user to control and interact with the console without having to touch a game controller, but just using gestures or voice commands. This device is powered by both hardware and software that execute fundamental tasks planned for the experiment. It generates a 3-D image of objects in its field of view. Furthermore, the Kinect have also a stereo microphone to allow conversations and voice commands. It is provided with an infrared light source, 3-D depth camera, and a RGB camera.

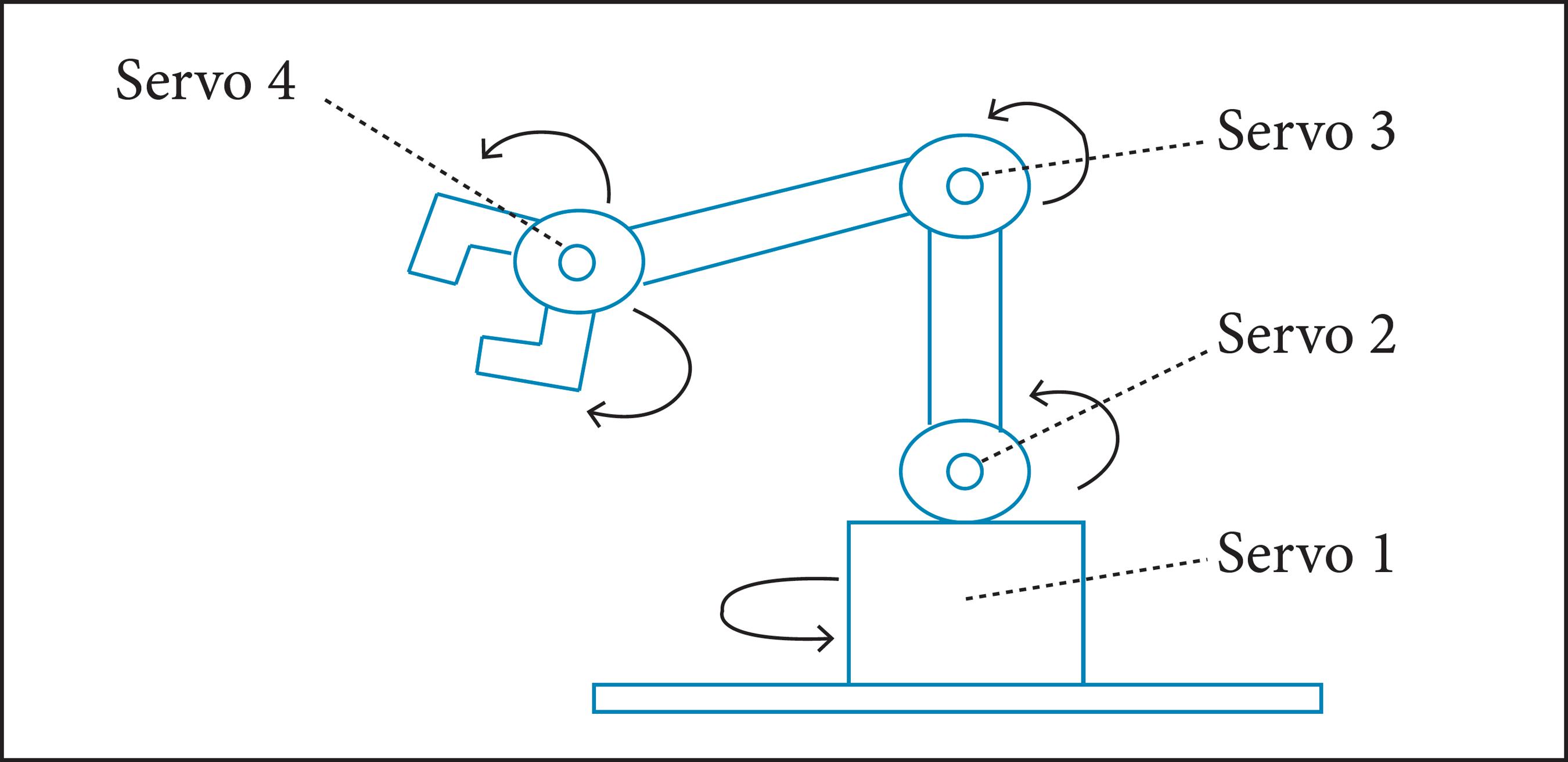
The robotic manipulator used in this experiment is an open development as an open-hardware project (http://www.instructables.com/id/Pocket-Sized-Robot-Arm-meArm-V04/). Figure 5 shows the communication hardware. The user sends the commands to the Arduino by using a computer equipped with the Bluetooth technology. The four servos receive the user commands through the interface with one of the Arduinos. These are connected by wire while the Bluetooth is a wireless-communication technology.

The DOFs of the manipulator are a rotation on its own base - two angular DOFs related to the other two link joints and the hand motion as shown in Fig. 6. The complete problem involves one more DOF related to the platform response to the robotic manipulator motion. In this paper an ice platform is used instead of a floating system (till in development).

Figure 7 shows the real robotic manipulator used in the lab experiment and the associated hardware. The measurements of the reactive linear effects of the manipulator were computed by using a camera to record the motion. The video was then treated to obtain the reaction effects of the manipulator motion on the non-inertial platform. The same procedure was used for the computation of the rotational effect of the links motion on the platform. Figure 8 illustrates the experiment assemblage to record the video.

Figure 7
The robotic manipulator and the associated hardware that were assembled on an ice platform.

Figure 8
Assemblage of the experiment to record and measure the ice platform response to the robotic manipulator motion.

For future experiments the manipulator platform is planned to use a compressed air system so as to allow the robot to float on a thin shell of air. However, in this very first prototype, ice platforms are used to represent the non-inertial base as proposed in the scope of this paper. The experiments being conducted in the lab aim to analyze the impact of the robotic arms on the platform rotational and translational motions. For this study the Kinect was not used. It will be used in future experiments with air-supported manipulators. Instead of using Kinect the motion was recorded by using a camera. Then the Kinovea software (www.software.informer.com) has been used to process the images, generate tables and then the graphics. Figure 9 illustrates the response of the ice platform to the motion of the robotic links (deployment/retraction of the links).

Figure 9
Motion of the ice platform in response to the robotic manipulator motion.

The experiments confirmed that the ice low friction allows the platform to move in response to the robotic manipulator link motions. The robotic manipulator shown in Fig. 7 was not designed so as to cancel the reactions on the ice platform passively.

SIMULATIONS, RESULTS, AND DISCUSSION

The mathematical model given by Eqs. 6 to 11 has been simulated through computer by considering two scenarios. One in which the robotic manipulator is not working (arms retracted). The other in which the arm is being deployed from a position 0º to 180º. In this case the arm deployment configuration does not cancel the reaction, and the base moves in response to the arms retraction. The objective is to analyze the control efforts to keep the satellite attitude within the prescribed.

The data used for the simulation are shown in Table 1, in which the symbols in the first to the fourth line are the three initial moments and the product of inertia, respectively, J_tx0, J_ty0, J_tz0, and J_txz0; Θ₁₀ and Θ₂₀ are the initial angles for the robotic manipulator links.

Table 1
Data used for the computer simulations.

Initial parameters	Initial values	Units
Jtx 0	7.5	kgm2
Jty 0	7.7	kgm2
Jtz 0	8.0	kgm2
Jtxz 0	0.035	kgm2
θ1 0	0; 180	Degrees
θ2 0	0; 180	Degrees
Roll	0; 5	Degrees
Pitch	0; 5	Degrees
Yaw	0; 6	Degrees

Figures 10 and 11 show the attitude control and the associated control effort for the satellite with the robotic manipulator off.

Figure 10
Attitude control by considering the robot manipulator out of work.

Figure 11
Control effort associated with the case shown in Fig. 10.

Figures 12 and 13 show the attitude control and the control efforts by considering the robotic manipulator working, that is, with the manipulator moving. From results shown in Fig. 13, it is clear that the associated control effort is larger by approximately one order compared to the case when the robotic manipulator arms are not moving (Fig. 10). Actually it was expected that the control effort to keep the platform stabilized during the action of the robotic manipulator arms would increase. Note that the maximum control effort to control the attitude for the case the arms were not moving is 0.06 Nm while for the case in which the arms were moving is 0.36 Nm. Another comment is that the time required to take the spacecraft attitude to the prescribed values (roll, pitch, and yaw equal to zero) is larger for the case when the robotic manipulator is working.

Figure 12
Attitude control by considering the robotic manipulator working.

Figure 13
Control effort associated with the case shown in Fig. 12.

Figure 14 shows the scenario in which the link motions cancel the reactions on the platform. The procedure to obtain the result was as follows: the attitude was set at zero positions in roll, pitch, and yaw. Then the operation to move the arms from zero position to about 180º was performed. The first manipulator link moves in counterclockwise direction while the second one moves in the clockwise direction, with synchronized motion. The result confirms the platform stability in the absence of any external perturbation. This approach is passive in the sense that no control action is needed to compensate the effect of the reaction torque on the robot base since that reaction is eliminated by the synchronized and reverse motion of the manipulator links.

Figure 14
Result for the scenario in which the motion of the arms cancels the reactions on the platform.

CONCLUSION

This study deals with the dynamics analysis of on-orbit robotic manipulator operations by considering the manipulator mounted on a non-fixed base. An experiment at the SRL laboratory (Divisao de Mecânica Aeronáutica, Instituto Tecnológico de Aeronáutica) was conducted to analyze the dynamics of a robotic manipulator assembled on an ice platform aiming the analysis of the ice platform response to the motion of the robotic manipulator arms. A mathematical model for a spacecraft like robotic manipulator was developed for the sake of attitude dynamics simulations. The goal is the study of the motion impact of the robotic manipulator arms on the attitude control effort and on the required time to take small attitude angles to zero. The results for the case when the robotic arms are moving/not moving were compared in the analysis. Through simulations it was verified that the control effort increases for the case when the robotic manipulator arms are moving. Also it was verified that the required time to take satellite attitude to zero increases for the same case. The simulations also focused on the case where the arms motions were synchronized and in opposite directions so as to cancel the torque reactions on the manipulator platform. The simulations results showed that the attitude is not affected by the motion of the robotic manipulator arms in this case.

ACKNOWLEDGEMENTS

To the Institutos Nacionais de Ciência e Tecnologia (INCT) for Space Studies, Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), Instituto Tecnológico de Aeronáutica (ITA), and Departamento de Computação, Pontifícia Universidade Católica de São Paulo (PUC-SP) for the support to this research.

0443 REFERENCES

• Alexander H, Cannon R (1987) Experiments on the control of a satellite manipulator. Proceedings of the American Control Conference; Seattle, USA.
• Arantes Jr G (2011) Rendezvous with a non-cooperating target (PhD thesis). Bremen: International University of Bremen.
• Da Fonseca IM (1998) Integrated structural/control optimization of a large space structure with articulation subject to the gravity-gradient torque. São José dos Campos: Instituto Tecnológico de Aeronáutica.
• Dubowsky S, Papadopoulos E (1993) The kinematics, dynamics, and control of free-flying and free-floating space robotics systems. IEEE Trans Robot Autom 9(5):531-543. doi: 10.1109/70.258046
  » https://doi.org/10.1109/70.258046
• Goddard Jr JS (1997) Pose and motion estimation from vision using dual quaternion-based extended Kalman filtering (PhD thesis). Knoxville: The University of Tennessee.
• Kaplan MH (1976) Modern spacecraft dynamics & control. New York: John Willey & Sons.
• Kawano I, Mokuno M, Horiguchi H, Kibe K (1994) In-orbit demonstration of an unmanned automatic rendezvous and docking system by the Japanese Engineering Test Satellite ETSVII. Proceedings of the AIAA-94-3648-CP; Scottsdale, USA.
• Kawano I, Mokuno M, Kasai T, Suzuki T (2001) Result of autonomous rendezvous docking experiment of engineering test satellite - VII. J Spacecraft Rockets 38(1):105-111. doi: 10.2514/2.3661
  » https://doi.org/10.2514/2.3661
• Kawano I, Mokuno M, Toru K, Takashi S (1998) First result of autonomous rendezvous docking experiments on NASDA's ETSVII satellite. Proceedings of the 49th International astronautical Congress. IAF-98-A3.09; Melbourne, Australia.
• Kawano I, Wakabayashi Y, Kasai T, Suzuki T (1989) In-orbit demonstration concept for the space platform in NASDA - rendezvous docking system. Proceedings of the International Astronautical Federation. IAF-89-017; Malaga, Spain.
• Longman RW (1994) A tutorial overview of the dynamics and control of satellite-mounted robots. In: Skaar S, Ruoff CF, editors. Teleoperation and robotics in space. Progress in Astronautics and Aeronautics. vol. 161. Washington: AIAA. p. 237-258.
• Meirovitch L (1970) Methods of analytical dynamics. New York: McGraw-Hill.
• Mokuno M, Kawano I, Hiroshi H, Kibe K (1995) Development of the ETS-VII RVD system by the Japanese Engineering Test Satellite ETS-VII. Proceedings of the AIAA-95-3357; Baltimore, USA.
• Mukherjee R, Zurowski M (1994) Reorientation of a structure in space using a three-link rigid manipulator. J Guid Contr Dynam 17(4):840-847. doi: 10.2514/3.21274
  » https://doi.org/10.2514/3.21274
• National Aeronautics and Space Administration (2005) Press kit; [accessed 2007 May 5]. www.nasa.gov/news/0600515_dart_ mishap_summary.html
  » www.nasa.gov/news/0600515_dart_ mishap_summary.html
• Pedersen L, Lortenkamp D, Wettergreen D, Nourbakhsh I, Smith T (2004) NASA Exploration Team (NEXT) Space Robotics Technology assessment Report. NASA/TM-2004.
• Qureshi F, Terzopoulos D (2008) Intelligent perception and control for space robotics. Mach Vis Appl 19(3):141-161. doi: 10.1007/s00138-007-0085-z
  » https://doi.org/10.1007/s00138-007-0085-z
• Skaar SB, Ruoff CF (1994) Teleoperation and robotics in space. Progr Astronaut Aeronaut 61:443-489. doi: 10.2514/4.866333
  » https://doi.org/10.2514/4.866333
• Umetani Y, Yoshida KA (1987) Continuous path control of space manipulators mounted on OMV. Acta Astronaut 15(12):981-986. doi: 10.1016/0094-5765(87)90022-1
  » https://doi.org/10.1016/0094-5765(87)90022-1
• Vafa Z, Dubowsky S (1987) On the dynamics of manipulators in space using the virtual manipulator approach. Proceedings of the IEEE International Conference on Robotics and automation; San Francisco, USA.
• Wie B (1998) Space vehicle dynamics and control. AIAA Education Series. Reston: AIAA.
• Yoshida K (2009) Achievements in space robotics. IEEE Robot Autom Mag 16(4):20-28. doi: 10.1109/MRa.2009.934818
  » https://doi.org/10.1109/MRa.2009.934818

Publication Dates

• Publication in this collection
  Oct-Dec 2015

History

• Received
  30 Dec 2014
• Accepted
  11 Nov 2015