Abstract
We consider the three dimensional electromagnetic inverse scattering problem of determining information about a buried coated object from a knowledge of the electric and magnetic fields measured on the surface of the earth corresponding to time harmonic electric dipoles as incident fields. We assume that the buried object is a perfect conductor that is (possibly) partially coated by a thin dielectric layer. No a priori assumption is made on the extent of the coating, i.e. the object can be fully coated, partially coated or not coated at all. We present an algorithm based on the linear sampling method and reciprocity gap functional for reconstructing the shape of the scattering obstacle together with an estimate of the surface impedance of the coating.
inverse scattering; mixed boundary conditions; buried objects
Target identification of buried coated objects* * This research was supported in part by the U.S. Air Force Office of Scientific Research under Grant FA9550-05-1-0127.
Fioralba Cakoni; David Colton
Department of Mathematical Sciences, University of Delaware, Newark, Delaware 19716, USA, E-mails: cakoni@math.udel.edu / colton@math.udel.edu
ABSTRACT
We consider the three dimensional electromagnetic inverse scattering problem of determining information about a buried coated object from a knowledge of the electric and magnetic fields measured on the surface of the earth corresponding to time harmonic electric dipoles as incident fields. We assume that the buried object is a perfect conductor that is (possibly) partially coated by a thin dielectric layer. No a priori assumption is made on the extent of the coating, i.e. the object can be fully coated, partially coated or not coated at all. We present an algorithm based on the linear sampling method and reciprocity gap functional for reconstructing the shape of the scattering obstacle together with an estimate of the surface impedance of the coating.
Mathematical subject classification: Primary: 35R30, 35Q60; Secondary: 35P25;78A45.
Key words: inverse scattering, mixed boundary conditions, buried objects.
1 Introduction
The use of electromagnetic fields to detect buried objects has a long history and continues to be an active area of research [3], [7], [8]. Of particular interest is the use of such methods to detect chemical waste deposits, examine urban infrastructure and locate landmines. However, from a practical point of view, there are two main reasons why such imagining problems remain basically unresolved. The first of these problems is the difficulty of distinguishing the scattered field due to the target from the scattered fields due to the earth, the antenna and, in particular, the air-earth interface. A second problem is that the material properties of the target are in general unknown. For example, a landmine can be made of wood, metal or plastic whereas a rusted barrel of chemical waste deposits is typically modeled by a complicated mixed boundary value problem involving a dielectric of unknown permittivity. Due to such problems, traditional methods of imagining such as the use of weak scattering approximations and nonlinear optimization techniques remain problematic.
In recent years a new class of electromagnetic imaging techniques has been developed which has the potential of overcoming the problems mentioned in the above paragraph. These new techniques can be described as ''qualitative methods in inverse scattering theory'' [4] and have a number of remarkable features which make them attractive for the imaging of buried objects. We will focus our attention on the most popular of these qualitative methods called the linear sampling method [6], [11], [15]. The remarkable feature of the linear sampling method is that 1) it is a linear method that does not ignore multiple scattering effects and 2) it determines the shape of a target without requiring any a priori knowledge of the target's physical properties. However, until very recently, the implementation of the linear sampling method for a nonhomogeneous background media required a knowledge of the Green's function for the background media. This is obviously an unattractive feature if it is desired to use this method for the detection of buried objects, particularly if the scattering effects due to the antenna play a significant role.
In order to overcome the problem of needing to compute the Green's function for the background media, a new version of the linear sampling method based on the reciprocity gap functional was introduced by Colton and Haddar [10] for the scalar case and by Cakoni, Fares and Haddar [7] for the vector case. However, in imagining nothing is free and the price paid for avoiding the need to compute the Green's function is that one now needs to measure both the electric and magnetic fields corresponding to time harmonic electric dipoles as incident fields. In the case when the buried object is a perfect conductor or a penetrable, anisotropic inhomogeneous medium, the efficaciousness of this approach to the imaging of buried objects was shown in [7]. The purpose of this paper is to consider the case when the buried object is a perfect conductor that may be partially coated by a thin dielectric layer. The inverse scattering problem in this case is considerably more complicated than the simple case of a perfect conductor since it is unknown a priori whether or not the target is coated. In particular, the inverse problem is now to not only determine the shape of the target but also whether or not the target is coated and if so the value of the surface impedance of the coating [13]. As in [7], we will consider the case when the electric and magnetic fields are both known on the entire boundary of an absorbing homogeneous region of the background media that is known a priori to contain the target. The case of an object buried in the earth is then handled by assuming that the part of the boundary below the surface of the earth is far away from the incident sources and hence we can assume that the total electric and magnetic fields are very small on this portion of the boundary.
It gives the authors particular pleasure to present our work on the detection of buried objects using electromagnetic fields in the proceedings of a conference dedicated to the twenty fifth anniversary of Alberto Calderon's seminal paper on the same topic [8]. As is seen by the papers in this volume, Calderon's paper of 1980 has been a major influence not only on our own work but also on the work of many other mathematicians and scientists working in diverse disciplines. We are happy to be part of this celebration!
2 Formulation of the direct and inverse scattering problems
We consider the scattering of a time-harmonic electromagnetic field of frequency w by a scattering object embedded in a piecewise homogeneous background medium in
3. We assume that the magnetic permeability µ0 > 0 of the background medium is a positive constant whereas the electric permittivity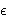 (x) and conductivity s(x) are piecewise constant. Moreover we assume that for |x| = r > R, for R sufficiently large, s = 0 and
(x) and conductivity s(x) are piecewise constant. Moreover we assume that for |x| = r > R, for R sufficiently large, s = 0 and 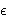 (x) =
(x) = 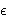 0. Then the electric field
0. Then the electric field 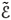 and magnetic field
and magnetic field 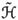 in the background medium satisfy the time-harmonic Maxwell's equations
in the background medium satisfy the time-harmonic Maxwell's equations
After an appropriate scaling [12] and elimination of the magnetic field we now obtain the following equation for the electric field 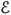 in the background medium
in the background medium
curl curl 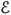 K2n (x)
K2n (x) 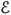 = 0
= 0
where
Note that the piecewise constant function n(x) satisfies n(x) = 1 for r > R, Â(n) > 0 and Á(n) > 0. The surfaces across which n(x) is discontinuous are assumed to be piecewise smooth and closed.
Now let D be a scattering object embedded in the above piecewise homogeneous background such that  3\
3\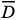 is connected. We suppose that the boundary ¶D of D is piecewise smooth and denote by n the outward unit normal. Furthermore, we assume that the boundary ¶D = GDÈPÈGI is split in two open disjoint parts GD and GI having P as their possible common boundary in ¶D. The domain D is the support of a perfect conductor (possibly a disconnected object) that is partially coated on a portion GI of the boundary by a very thin layer of dielectric material. We assume for sake of presentation that the coating is homogeneous. Let the positive constant l > 0 describe the surface impedance of the coating. The incident field is considered to be an electric dipole located at x0Î L with polarization p Î
is connected. We suppose that the boundary ¶D of D is piecewise smooth and denote by n the outward unit normal. Furthermore, we assume that the boundary ¶D = GDÈPÈGI is split in two open disjoint parts GD and GI having P as their possible common boundary in ¶D. The domain D is the support of a perfect conductor (possibly a disconnected object) that is partially coated on a portion GI of the boundary by a very thin layer of dielectric material. We assume for sake of presentation that the coating is homogeneous. Let the positive constant l > 0 describe the surface impedance of the coating. The incident field is considered to be an electric dipole located at x0Î L with polarization p Î  3 given by
3 given by
where  = k2ns and L is an open surface (to be made precise later on) situated in a layer with constant index of refraction ns. We denote by
= k2ns and L is an open surface (to be made precise later on) situated in a layer with constant index of refraction ns. We denote by  (x,x0) the free space Green's tensor of the background medium and define Ei(x): = Ei(x,x0,p) =
(x,x0) the free space Green's tensor of the background medium and define Ei(x): = Ei(x,x0,p) =  (x,x0)p which satisfies
(x,x0)p which satisfies
where d denotes the Dirac distribution. Note that Ei can be written as
where  =
=  (·, x0,p) is the electric scattered field due to the background medium.
(·, x0,p) is the electric scattered field due to the background medium.
We now consider a bounded domain W such that 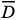 is contained in W and the open surface L is contained in
is contained in W and the open surface L is contained in  3\
3\ . Let ¶W denote the piecewise smooth boundary of W. Note that L or a portion of L may be a subset of ¶W. We assume the medium inside the domain W containing the scattering object D is homogeneous with constant index of refraction nb and define
. Let ¶W denote the piecewise smooth boundary of W. Note that L or a portion of L may be a subset of ¶W. We assume the medium inside the domain W containing the scattering object D is homogeneous with constant index of refraction nb and define  = k2nb (see Fig. 1).
= k2nb (see Fig. 1).
Then the total electric field E = Es+Ei, where Es is the scattered field due to the obstacle D, satisfies the following equation and mixed boundary conditions:
In addition, the scattered field Es satisfies the Silver Müller radiation condition
uniformly in  = x/|x|, r = |x|.
= x/|x|, r = |x|.
In order to formulate precisely the above scattering problem we are concerned with throughout this paper, we need the following spaces:
We introduce the space
equipped with the norm
For the exterior domain De we define the above spaces in the same way for every De Ç BR, with BR a ball of arbitrary radius R and denote these spaces by Hloc(curl,De) and Xloc(De,G2), respectively. The traces n×u|¶D and n×(u×n)|¶D of u Î H(curl,D) (or u Î Hloc(curl, D)) are in the Hilbert spaces
respectively, with curl¶D denoting the surface curl. Note that by an integration by parts we can define a duality relation between  (¶D) and
(¶D) and  (¶D) (see [17] in the case when the boundary is smooth, and [2] in the case when the boundary is piecewise smooth). Finally, we introduce the trace space of X(D,GI) on GD by
(¶D) (see [17] in the case when the boundary is smooth, and [2] in the case when the boundary is piecewise smooth). Finally, we introduce the trace space of X(D,GI) on GD by
where the ball BR contains D and H0(curl,BR) is the space of functions u in H(curl,BR) satisfying n× = 0. Obviously, Y(GD) is a Banach space with the norm
= 0. Obviously, Y(GD) is a Banach space with the norm
where the infimum is taken over all functions u Î H0(curl,BR) such that n× Î
Î  (GI) and h = n×
(GI) and h = n× . Y(GD) is also a Hilbert space and its dual space Y'(GD) can be precisely characterized. In particular a function f Î Y(GD)' can be extended to a function
. Y(GD) is also a Hilbert space and its dual space Y'(GD) can be precisely characterized. In particular a function f Î Y(GD)' can be extended to a function  Î
Î  (¶D) defined on the whole boundary and satisfying
(¶D) defined on the whole boundary and satisfying  Î
Î  (GI) (see [6] for details).
(GI) (see [6] for details).
The direct scattering problem can be formulated as given Ei defined by (3) find Es = E-Ei Î X( 3\
3\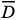 ) satisfying (4)-(7). In a similar way as in [6] it can be shown that the direct scattering problem has a unique solution.
) satisfying (4)-(7). In a similar way as in [6] it can be shown that the direct scattering problem has a unique solution.
Remark 2.1. It is also possible to consider the problem of objects buried in an unbounded multi-layer medium. In this case, the radiation condition and mathematical analysis of the forward problem become more complicated (see [14] for the case of two layered medium). However the following analysis of the inverse scattering problems remains the same.
In order to formulate the inverse problem we assume that both the tangential components n×E and n×curl E of the total electric field E = E(· , x0,p) and magnetic field H =  curl E, respectively, are known on ¶W for all point sources x0Î L. Furthermore, without loss of generality, we assume that L is a closed surface surrounding W situated in a layer with index of refraction ns. By an analyticity argument the following analysis also holds true if the point sources are located on an open analytic surface provided it can be extended to a closed (analytic) surface as above.
curl E, respectively, are known on ¶W for all point sources x0Î L. Furthermore, without loss of generality, we assume that L is a closed surface surrounding W situated in a layer with index of refraction ns. By an analyticity argument the following analysis also holds true if the point sources are located on an open analytic surface provided it can be extended to a closed (analytic) surface as above.
The inverse scattering problem we are interested in is to determine D and l from a knowledge of the tangential components n×E and n×curl E of the total electric field E = E(·, x0,p) and magnetic field H =  curl E measured on ¶W for all point sources x0Î L and two linearly independent polarizations p tangent to L at x0. Here n denotes the outward unit normal to ¶W. We remark that in what follows n is always the outward unit normal to the surface under consideration unless otherwise stated. We remark that by modifying the approach in [12] it is possible to prove that the above data uniquely determines D and than the uniqueness for l follows in the same way as in [16]. Here we are mainly concern with the solution of the inverse problem.
curl E measured on ¶W for all point sources x0Î L and two linearly independent polarizations p tangent to L at x0. Here n denotes the outward unit normal to ¶W. We remark that in what follows n is always the outward unit normal to the surface under consideration unless otherwise stated. We remark that by modifying the approach in [12] it is possible to prove that the above data uniquely determines D and than the uniqueness for l follows in the same way as in [16]. Here we are mainly concern with the solution of the inverse problem.
3 The reciprocity gap functional
Let E = E(·,x0,p) = Es(·,x0,p)+ (· ,x0)p and H = 1/ik curl E be the total electric and magnetic fields, respectively, corresponding to the scattering problem (4)-(7). Note that we suppress the dependence of the total field on the wave number ks of the medium where the point source is located. For any function W Î H(curl, W), we can define the gap reciprocity functional by
(· ,x0)p and H = 1/ik curl E be the total electric and magnetic fields, respectively, corresponding to the scattering problem (4)-(7). Note that we suppress the dependence of the total field on the wave number ks of the medium where the point source is located. For any function W Î H(curl, W), we can define the gap reciprocity functional by
Since E Î H(curl, W), the integral is interpreted in the sense of the duality between  (¶W) and
(¶W) and  (¶W). Note that E depends on x0 and hence so does
(¶W). Note that E depends on x0 and hence so does  . Next, in order to connect
. Next, in order to connect  with the scattering problem, we define the subspace
with the scattering problem, we define the subspace  (W) Ì H(curl, W) by
(W) Ì H(curl, W) by
where UT: = (n×U)×n. The reciprocity gap functional restricted to  (W) can be seen as an operator R :
(W) can be seen as an operator R :  (W) ®
(W) ®  (L) defined by
(L) defined by
for all x0Î L.
In order to derive an integral equation from  , we need to use a parametric family of solutions in
, we need to use a parametric family of solutions in  (W) which satisfy certain properties to be made precise later. In particular, we consider the electric Herglotz function
(W) which satisfy certain properties to be made precise later. In particular, we consider the electric Herglotz function  g defined by
g defined by
where S2 is the unit sphere. Now, letting
denote the electric dipole corresponding to kb, we look for a solution g Î  (S2) of
(S2) of
Alternatively, we can define the single layer potential by
where
and  is a regular part of the boundary of some simply connected domain containing W in its interior, and look for a solution j Î
is a regular part of the boundary of some simply connected domain containing W in its interior, and look for a solution j Î  (
( ) of
) of
Note that both { g, g Î
g, g Î  (S2)} and {Aj, j Î
(S2)} and {Aj, j Î  (
( )} are subsets of
)} are subsets of  (W). To fix our ideas, we use in this paper only electric Herglotz functions. Hence, the reciprocity gap functional method is based on the characterization of D from the behavior of a solution j of (15) for different sampling points z Î W. We also emphasize that the background Green's function
(W). To fix our ideas, we use in this paper only electric Herglotz functions. Hence, the reciprocity gap functional method is based on the characterization of D from the behavior of a solution j of (15) for different sampling points z Î W. We also emphasize that the background Green's function  (· ,x0)p does not appear in (15).
(· ,x0)p does not appear in (15).
To study the integral equation (15), which is ill-posed since R is a smoothing operator, we first study the properties of R.
Lemma 3.1. Assume that GI is not empty. Then the operator R: (W) ®
(W) ®  (L) defined by (12) is injective.
(L) defined by (12) is injective.
Proof. R W = 0 means  (E(·, x0, p(x0)), W) = 0 for all (x0, p(x0)). Since both E and W satisfy Maxwell's equation in W\
(E(·, x0, p(x0)), W) = 0 for all (x0, p(x0)). Since both E and W satisfy Maxwell's equation in W\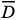 , we have, using the boundary condition for E on ¶D,
, we have, using the boundary condition for E on ¶D,
where first integral is interpreted in sense of duality between Y(GD) and Y(GD)' while the second integral in the sense of  (GI). Next let
(GI). Next let  be the unique solution to (see [6])
be the unique solution to (see [6])
Then from the above problem, the boundary conditions for the total field E = Es+ (·, x0)p and (18) we have that
(·, x0)p and (18) we have that
Now since Es and  are both radiating solutions to the same equation the above equation simplifies to
are both radiating solutions to the same equation the above equation simplifies to
Since p is an arbitrary polarization on the tangent plane to L at x0, we obtain n× (x0) = 0 for x0Î L. Furthermore, since
(x0) = 0 for x0Î L. Furthermore, since  is a radiating solution to Maxwell's equations outside the domain bounded by L, we conclude by the uniqueness of the scattering problem for a perfect conductor (c.f. [12]) that
is a radiating solution to Maxwell's equations outside the domain bounded by L, we conclude by the uniqueness of the scattering problem for a perfect conductor (c.f. [12]) that  = 0 outside the domain bounded by L. Then the unique continuation principle implies that
= 0 outside the domain bounded by L. Then the unique continuation principle implies that  = 0 outside D, whence both n×W = 0 on GD and n×curl W- ikbl(n×W)×n = 0. Finally from the uniqueness of the interior mixed boundary value problem for W we conclude that W = 0 which proves the lemma.
= 0 outside D, whence both n×W = 0 on GD and n×curl W- ikbl(n×W)×n = 0. Finally from the uniqueness of the interior mixed boundary value problem for W we conclude that W = 0 which proves the lemma.
Lemma 3.2. Assume that GI is not empty. Then the operator R: (W) ®
(W) ®  (L) defined by (12) has dense range.
(L) defined by (12) has dense range.
Proof. Consider b Î  (L) and assume that
(L) and assume that
From (12) and the bi-linearity of  one has
one has
where
and a = (b·p) p. Using the second vector Green's formula and the boundary conditions for E one concludes that
for all W Î  (W), where again the first integral is interpreted in sense of duality between Y(GD) and Y(GD)' while the second integral in the sense of
(W), where again the first integral is interpreted in sense of duality between Y(GD) and Y(GD)' while the second integral in the sense of  (GI). Since
(GI). Since  (W) contains the Herglotz wave functions given by (13), from Theorem 2.8 in [6]and the well posedness of the interior mixed boundary value problem one has that the set
(W) contains the Herglotz wave functions given by (13), from Theorem 2.8 in [6]and the well posedness of the interior mixed boundary value problem one has that the set
is dense in Y(GD)×L2(GI). Therefore
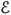 = 0 on GI
= 0 on GI
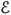 = 0 on GD
= 0 on GD
The boundary conditions for 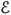 imply that both n×
imply that both n×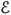 = 0 and n×curl
= 0 and n×curl 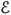 = 0 on ¶D. This means that the extension of
= 0 on ¶D. This means that the extension of 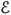 by 0 inside D satisfies Maxwell's equations inside the domain bounded by L with the index n set equal to nb inside D. From the unique continuation principle one has that
by 0 inside D satisfies Maxwell's equations inside the domain bounded by L with the index n set equal to nb inside D. From the unique continuation principle one has that 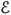 is 0 inside the domain bounded by L and outside D. Noting that
is 0 inside the domain bounded by L and outside D. Noting that
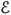 (x) =
(x) =  (ES(x, x0, a(x0)) +
(ES(x, x0, a(x0)) +  (x, x0) a (x0))ds(x0)
(x, x0) a (x0))ds(x0)
one concludes that 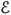 ×n is continuous across L. The uniqueness theorem for the exterior problem for Maxwell's equations with boundary data n×
×n is continuous across L. The uniqueness theorem for the exterior problem for Maxwell's equations with boundary data n×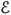 = 0 on L implies that
= 0 on L implies that 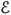 = 0 outside the domain bounded by L as well. Finally, from the jump relations of the vector potential across L [12] we have that
= 0 outside the domain bounded by L as well. Finally, from the jump relations of the vector potential across L [12] we have that
Hence (b·p) p = 0 for all p tangential to L which implies that b = 0. This ends the proof.
Remark 3.1. It is easy to prove (see e.g. Theorem 4.8 in [4]) that the operator R:  (W) ®
(W) ®  (L) is compact.
(L) is compact.
4 Solution of the inverse problem
We now investigate the solvability of
with respect to g where Ee(·, z,q,kb) is given by (14) and  g is the electric Herglotz function with kernel g given by (13). To this end, we recall the interior mixed boundary value problem for z Î D
g is the electric Herglotz function with kernel g given by (13). To this end, we recall the interior mixed boundary value problem for z Î D
It is shown in [6] that there is a unique solution Ez Î X(D,GI) of the above problem. We can now prove the following result:
Theorem 4.1. Assume that GI¹ Æ and let E = E(· ,x0,p) and H = 1/ik curl E be the total electric and magnetic fields, respectively, corresponding to the scattering problem (4)-(7). Then
1. For z Î D and a given 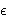 > 0, there exists a
> 0, there exists a  Î
Î  (S2) such that
(S2) such that
and the corresponding electric Herglotz wave function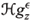 converges to the solution of (22)-(24) in X(D,GI) as
converges to the solution of (22)-(24) in X(D,GI) as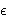 ® 0.
® 0.
2. For a fixed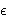 > 0, we have that
> 0, we have that
3. For z Î  3\
3\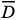 and a given
and a given 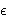 > 0, every
> 0, every Î
Î  (S2) that satisfies
(S2) that satisfies
is such that
Proof. Let z Î D. Since W Î  (W) and Ee(·, z,q,kb) satisfy curl curl W-kbW = 0 in W\
(W) and Ee(·, z,q,kb) satisfy curl curl W-kbW = 0 in W\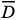 , integrating by parts and using the boundary condition for the total field we have that
, integrating by parts and using the boundary condition for the total field we have that
From the proof of Lemma 3.1 we see that  (E,W) =
(E,W) =  (E,Ee(·, z,q,kb)) has a unique solution W if and only if there exists a W Î
(E,Ee(·, z,q,kb)) has a unique solution W if and only if there exists a W Î  (W) such that n×W-n×Ee(·, z,q,kb) = 0 on GD and n×curl [Ez-Ee(·, z,q, kb)]-ikbl[n×(Ez-Ee(·, z,q, kb)]×n = 0 on GI which is in general not true. However in [6], Theorem 2.8, it is proved that the family
(W) such that n×W-n×Ee(·, z,q,kb) = 0 on GD and n×curl [Ez-Ee(·, z,q, kb)]-ikbl[n×(Ez-Ee(·, z,q, kb)]×n = 0 on GI which is in general not true. However in [6], Theorem 2.8, it is proved that the family
is dense in Y(GD)× (GI). Hence, for every
(GI). Hence, for every 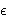 > 0 there exists a Herglotz function
> 0 there exists a Herglotz function 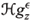 such that n×
such that n×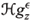 approximates n×Ee(·, z,q) with respect to the Y(GD) norm and n×curl
approximates n×Ee(·, z,q) with respect to the Y(GD) norm and n×curl  g-ikbl(n×
g-ikbl(n× g)×n approximates n×curl Ee(·, z,q,kb)-ikbl(n×Ee(·, z,q, kb))×n with respect to the
g)×n approximates n×curl Ee(·, z,q,kb)-ikbl(n×Ee(·, z,q, kb))×n with respect to the  (GI) norm. In particular, from (18),
(GI) norm. In particular, from (18),  is an approximate solution to (21) and
is an approximate solution to (21) and 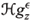 converges to the solution of (22)-(24) in the X( D,GI) norm as
converges to the solution of (22)-(24) in the X( D,GI) norm as 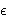 ® 0. Next, since n×Ee(·, z,q)® ¥ in the Y(GD) norm and n×curl Ee(·, z,q,kb)-ikbl(n×Ee(·, z,q, kb))×n ® ¥ in the
® 0. Next, since n×Ee(·, z,q)® ¥ in the Y(GD) norm and n×curl Ee(·, z,q,kb)-ikbl(n×Ee(·, z,q, kb))×n ® ¥ in the  (GI) norm as z approaches the boundary, we obtain from the well posedness of the interior mixed boundary value problem that, for a fixed
(GI) norm as z approaches the boundary, we obtain from the well posedness of the interior mixed boundary value problem that, for a fixed 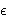 > 0,
> 0,  = ¥ and
= ¥ and  = ¥. Now we consider z Î W\
= ¥. Now we consider z Î W\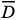 and let
and let  and its corresponding Herglotz function
and its corresponding Herglotz function 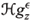 be such that
be such that
Note that from Lemma 3.2 we can always find such a 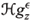 . Assume to the contrary that
. Assume to the contrary that  < C where the positive constant C is independent of
< C where the positive constant C is independent of 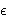 . From the trace theorems we have that the mixed trace of
. From the trace theorems we have that the mixed trace of 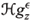 is also bounded in the corresponding norms. Noting that the total field can be written as E(·, x0,p) = Es(·, x0,p)+
is also bounded in the corresponding norms. Noting that the total field can be written as E(·, x0,p) = Es(·, x0,p)+  (·,x0)p and integrating by parts, weobtain that
(·,x0)p and integrating by parts, weobtain that
Due to the symmetry of the background Green's function, Es(x,x0,p) as a function of x0 solves curlx0 curlx0Es(x,x0,p)-k2n(x0)Es(x,x0,p) = 0 in the domain bounded by L and ¶D. Hence the first two integrals in the above equation give a solution W(x0) to the same equation as the one satisfied by Es(·, x0,p), whereas the last two integrals add up to - (z,x0)p by the Stratton-Chu formula and the fact that Ee(x,z,q,kb) is the fundamental solution of curl curl E-
(z,x0)p by the Stratton-Chu formula and the fact that Ee(x,z,q,kb) is the fundamental solution of curl curl E- E = 0. On the other hand we have that
E = 0. On the other hand we have that
Combining the above equalities we obtain that
Now since  < C there exists a subfamily, still denoted by
< C there exists a subfamily, still denoted by 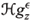 , that converges weakly to a V Î X(D,GI) as
, that converges weakly to a V Î X(D,GI) as 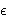 ® 0 and therefore n×
® 0 and therefore n×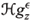 and n×curl
and n×curl 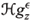 -ikbl(n×
-ikbl(n×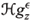 )×n converges weakly to n×V and n×curl V-ikbl(n×V)×n in the duality pairing Y(GD), Y(GD)' and
)×n converges weakly to n×V and n×curl V-ikbl(n×V)×n in the duality pairing Y(GD), Y(GD)' and  (GI), respectively. Let us set
(GI), respectively. Let us set
From (25) we now have that
Since  (x0) and W(x0) can be continued as radiating solutions to
(x0) and W(x0) can be continued as radiating solutions to
curlx0 curlx0ES (x, x0, p) K2n (x0) ES (x, x0, p) = 0
outside the domain bounded by L we deduce by uniqueness and the unique continuation principle that (28) holds true in
3\(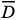 È{z0}). We now arrive at a contradiction by letting x0® z. Hence
È{z0}). We now arrive at a contradiction by letting x0® z. Hence 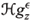 is unbounded in the X(D,GI) norm as
is unbounded in the X(D,GI) norm as 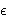 ® 0, which proves the theorem.
® 0, which proves the theorem.
Theorem 4.1 provides a characterization of the boundary ¶D of the scattering object D. Unfortunately, since the behavior of 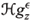 is described in terms of a norm depending on the unknown region D,
is described in terms of a norm depending on the unknown region D, 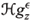 cannot be used to characterize D. Instead, we characterize the obstacle by the behavior of
cannot be used to characterize D. Instead, we characterize the obstacle by the behavior of  . In particular, given a discrepancy
. In particular, given a discrepancy 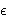 > 0 and
> 0 and  the e-approximate solution of (21), the boundary of the scatterer is reconstructed as the set of points z where the
the e-approximate solution of (21), the boundary of the scatterer is reconstructed as the set of points z where the  (S2) norm of
(S2) norm of  becomes large. In practice, since (21) is severely ill-posed due to the compactness of the operator R, one uses regularization methods to obtain a solution to (21). Obviously, an important question is whether this regularized solution will exhibit the properties of the
becomes large. In practice, since (21) is severely ill-posed due to the compactness of the operator R, one uses regularization methods to obtain a solution to (21). Obviously, an important question is whether this regularized solution will exhibit the properties of the 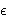 -approximate solution provided by Theorem 4.1. In general, this question is still open (However, see [1] for an answer to this question in the case of the scalar problem for a perfect conductor in homogeneous background using far field data). Numerical examples for similar reconstruction methods have shown in these cases that the computed regularized solution behaves in the way that the theory predicts [7], [9], [11], [15]. Note that the method determines D without any a priori knowledge of GD, GI or l.
-approximate solution provided by Theorem 4.1. In general, this question is still open (However, see [1] for an answer to this question in the case of the scalar problem for a perfect conductor in homogeneous background using far field data). Numerical examples for similar reconstruction methods have shown in these cases that the computed regularized solution behaves in the way that the theory predicts [7], [9], [11], [15]. Note that the method determines D without any a priori knowledge of GD, GI or l.
Assuming now that D is known, we want to determine the surface impedance l by making use of the approximate solution g of the equation (21). To this end let z Î D and Ez the unique solution of (22)-(24). Define Wz: = Ez-Ee(·, z,q, kb). Applying the second vector Green's formula in W\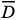 and the boundary conditions for Wz we have that
and the boundary conditions for Wz we have that
One can easily see that if E Î H(curl,D) and H =  curl E is a solution of Maxwell's equations and z Î D we have that
curl E is a solution of Maxwell's equations and z Î D we have that
and
n ×  (y) · curlyEe(y,z,q,kb) = iKbq · curlzF (y,z) (n ×
(y) · curlyEe(y,z,q,kb) = iKbq · curlzF (y,z) (n ×  (y))
(y))
and therefore from the Stratton-Chu formula
Furthermore, using again the second Green's formula in W\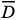 for Ee(·,z,q,kb) and
for Ee(·,z,q,kb) and  we obtain that
we obtain that
Finally, using (31) and the identity (30), (29) becomes
Noting that n×[Ez-Ee(·, z,q, kb)] is zero on GD, we have proven the following theorem:
Theorem 4.2. Let z Î D be a fix point and Ez be the corresponding solution of (22)-(24). Then
where the constant A(z,W, kb, q) which depends on the chosen W, z, kb and the polariazation q is given b
Note that (32) provides a formula for calculating l since Ez can be approximated by the Herglotz function  g where g is the approximate (regularized) solution of (21).
g where g is the approximate (regularized) solution of (21).
We end the paper with two remarks.
Remark 4.1. All the above analysis can be done if instead of  g one uses single layer potentials Aj and the same results hold for the solution j of (17). In fact there are many choices of the parameterization of the gap reciprocity functional
g one uses single layer potentials Aj and the same results hold for the solution j of (17). In fact there are many choices of the parameterization of the gap reciprocity functional  (E, W) in terms of W: = Fy where Fy Î
(E, W) in terms of W: = Fy where Fy Î  (W) with density function y in a Hilbert space H. The only requirement is that {Fy, y Î H } forms a dense subset of
(W) with density function y in a Hilbert space H. The only requirement is that {Fy, y Î H } forms a dense subset of  (W).
(W).
Remark 4.2. The above analysis for solving the equation (21) requires the measured tangential component of the total electric and magnetic field on the whole boundary ¶W of W. The case of an object buried in the earth is handled by assuming that the part of ¶W below the surface of the earth is far away from the incident sources and hence we can assume that the total electric and magnetic fields are very small on this portion of the boundary.
Numerical examples for determining D and l for partially coated buried objects using the above analysis will follow in a forthcoming paper. Note also that it is possible to treat the case of non constant inpedence. In this case one can only determine the essential suprimum of l (see [5] for the case of a homogeneous background).
Received: 01/IX/06. Accepted: 01/X/06.
#689/06.
- [1] T. Arens, Why linear sampling method works. Inverse Problems, 20 (2004), 163-173.
- [2] A. Buffa and P. Jr. Ciarlet, On traces for functional spaces related to Maxwell's equations. Part I: An integration by parts formula in Lipschitz polyhedra. Math. Meth. Appl. Sci., 24 (2001), 9-30.
- [3] C. Baum, Detection and Identification of Visually Obscured Targets Taylor and Francis, London, 1999.
- [4] F. Cakoni and D. Colton, Qualitative Methods in Inverse Scattering Theory Springer, Berlin, 2006.
- [5] F. Cakoni and D. Colton, The determination of the surface impedance of a partially coated obstacle from far field data. SIAM J. Appl. Math., 64 (2004), 709-723.
- [6] F. Cakoni, D. Colton and P. Monk, The electromagnetic inverse scattering problem for partly coated Lipschitz domains. Proc. Royal Soc. Edinburgh, 134A (2004), 661-682.
- [7] F. Cakoni, M.B. Fares and H. Haddar, Analysis of two linear sampling methods applied to electromagnetic imagining of burried objects. Inverse Problems, 22 (2006), 845-867.
- [8] A.P. Calderon, On an inverse boundary value problem, in Seminar on Numerical Analysis and its Applications to Continuum Physics, Soc. Brasileira de Matematica, Rio de Janeiro, 1980, 67-73.
- [9] F. Collino, M.B. Fares and H. Haddar, Numerical and analytical studies of the linear sampling method in electromagnetic scattering problems. Inverse Problems, 19 (2003) 1279-1299.
- [10] D. Colton and H. Haddar, An application of the reciprocity gap functional to inverse scattering theory. Inverse Problems, 21 (2005), 383-398.
- [11] D. Colton, H. Haddar and P. Monk, The linear sampling method for solving the electromagnetic scattering problem. SIAM J. Sci. Comp., 24 (2002), 719-731. 383-398.
- [12] D. Colton and R. Kress, Inverse Acoustic and Electromagnetic Scattering Theory, 2nd Edn. Springer Verlag, 1998.
- [13] D. Colton and P. Monk, Target identification of coated objects, IEEE Trans. Antennas Prop., 54 (2006), 1232-1242.
- [14] P. Cutzach and C. Hazard, Existence, uniqueness and analyticity properties for electromagnetic scattering in a two layered medium. Math. Meth. Appl. Sci., 21 (1998), 433-461.
- [15] H. Haddar and P. Monk, The linear sampling method for solving the electromagnetic inverse medium problem. Inverse problems, 18 (2002), 891-906.
- [16] R. Kress, Uniqueness in inverse obstacle scattering for electromagnetic waves in Proceedings of the URSI General Assembly Maastricht, 2002, Downloadable from the web site http://www.num.math.uni-goettingen.de/kress/researchlist.html
- [17] P. Monk, Finite Element Methods for Maxwell's Equations Oxford University Press, Oxford, 2003.
Publication Dates
-
Publication in this collection
19 Mar 2007 -
Date of issue
2006
History
-
Accepted
01 Oct 2006 -
Received
01 Sept 2006























































