On a continuum theory of brittle materials with microstructure

On a continuum theory of brittle materials with microstructure

Fernando Pereira Duda^I; Angela Cristina Cardoso de Souza^II

^IPrograma de Engenharia Mecânica, COPPE/UFRJ, Cx. Postal 68503 21945-970 Rio de Janeiro, Brasil E-mail: [e-mail]

^IILaboratório de Mecânica Teórica e Aplicada, PGMEC/TEM/UFF Rua Passo da Pátria 156, sala 409 - 24210-240 Niterói, Brasil E-mail: [e-mail]

ABSTRACT

This paper deals with a finite strain continuum theory of elastic-brittle solids with microstructure. A single scalar microstructural field is introduced, meant to represent - even if in a summary way - the concentration of microdefects within the material. A system of microforces, dual to the microstructural field, is axiomatically introduced. The corresponding balance, augmented with suitable constitutive information, yields, inter alia, a kinetic equation for the microstructural field, criteria for damage nucleation, growth and healing as well as a failure criterion based on attainment of a critical value of the microstructural field. The theory is applied for the description of the Mullins effect.

Mathematical subject classification: 74C15, 74C20.

Key Words: continuum mechanics, damage mechanics, brittle materials.

1 Introduction

There are many circumstances where the macroscopic behavior of solids is strongly influenced by processes on the microscale. This is the case, for instance, of the dynamic fracture behavior of brittle solids, where the macroscopic behavior is governed by nucleation, growth and coalescence of microcracks (see Ravi-Chandar, 1998).

In this paper we deal with the development of a finite strain continuum theory for the behavior of elastic-brittle solids that accounts for: microscale processes, by introducing a scalar microstructural field and the corresponding microforce system; rate and nonlocal effects, by including constitutive dependences on the rate and the gradient of the microstructural field. The microstructural field may represent, for instance, the cohesion state within the material: it varies from 1 (pristine material) to 0 (cracked-up material).

The main ingredients of our theory are the following: i) basic laws: the standard force and moment balances; the microforce balance; the dissipation inequality that includes, via the microforces, the power expended during microstructural changes, ii) constitutive theory: constitutive equations consistent with the dissipation inequality, that include both rate and gradient dependence on the microstructural field. The basic laws are postulated following the framework developed by Fried and Gurtin (1994) and Gurtin (1996). The microforce balance, augmented with suitable constitutive information, yields: a kinetic equation for the microstructural field; criteria for both cohesion decreasing (damage initiation and growth) and cohesion increasing (damage healing); the notion of elastic range; a failure criterion based on the attainment of a critical value of the microstructural field; a criterion for damage healing impossibility. Also, the model can describe distinct behavior under traction and compression.

An application of the presented theory for the description of the stress-softening phenomenon, also called the Mullins effect, is outlined. This phenomenon is typical for many materials such as rubbers, elastomers and biomaterials (see, for instance, Krishnaswamy and Beatty (2000), Beatty and Krishnaswamy (2000), DeSimone et al (2001) and references cited therein.).

The present modelling approach is similar to the dynamic fracture modelling approaches presented by Aranson et al (2000) and Karma et al (2001). But in contradistinction to their work, our approach is based on a clear separation of basic balance laws from constitutive equations, including dissipation. In this respect, our theory is similar to the isotropic damage theory presented by Costa-Mattos and Sampaio (1995), and Frémond and Nedjar (1996).

The paper is organized as follows. Section 2 introduces the basic notions of a continuum theory for an elastic material with microstructure. A general constitutive theory is presented in Section 3, where constitutive assumptions are introduced and restricted by using the Coleman-Noll (1963) principle. Section 4 presents the theory for the case in which the microstructural field is the cohesion descriptor. Application for the description of the Mullins effect is outlined in Section 5.

We adopt notations commonly used in continuum mechanics (see Gurtin, 1981). Symbols and quantities are defined when they first appear.

2 Basic notions

Let be a body identified with the bounded region of space it occupies in a fixed reference configuration. The macrokinematics is described by the motion y,

which maps the particle located at X Î at time t to its place x and is one-to-one at each t, with deformation gradient F : = Ñy consistent with det F > 0.The microkinematics is described by the macroscopic scalar field a, withgradient:

so that a(X,t) characterizes the observed microstructure at the particle X at time t.

We characterize the standard force system by the first Piola-Kirchhoff stress S and by body force per unit volume¹ b, both measured in the reference configuration. Then, the standard force and moment balances are, respectively,

where is an arbitrary part of , n the unitary exterior normal to the boundary of (¶), y₀ is an arbitrary spatial point and a×c represents the vectorial product of the vectors a and c. In local form, the standard force and moment balances are respectively:

where DivA denotes the divergence of the tensor or vector field A.

The working of the standard forces on a part is defined by the classical relation:

where A · B = tr (A^TB), for A and B tensors, and a · c is the usual internal product for the vectors a and c. The last equality is obtained by using (4)₁.

The microforce system is characterized by the microstress vector x, the (scalar) internal microforce p, the (scalar) external microforce m. The microforce system is constrained by the microforce balance:

which in local form is:

The working of the microforces on a part is given by:

where the last equality is obtained by using (7).

Within the present purely mechanical context, the Second Law, or Dissipation Inequality, takes the form:

where y is the free energy per unit referential volume. The corresponding local form is given by:

3 Constitutive theory

We consider constitutive equations giving y, S, x and p at any given point and time when:

are known at that point and time; i.e.,

We assume that: , and are smooth functions; 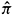is smooth when 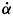¹ 0 with jump discontinuity at 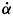= 0. Thus, p is constitutively determined only when 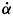¹ 0. Otherwise, it is constitutively indeterminate and defined by (7).

By inserting (12) into the dissipation inequality (10) we obtain the functional inequality:

Following the Coleman-Noll procedure we conclude that:

(i) the response function does not depend on 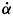, i.e,

(ii) the response function and must be related through.

(iii) the response functions and must be related through

(iv) the response functions 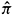must comply with the residual inequality

which implies that²:

It is convenient to use the additive decomposition of

_d:

into rate-independent ( ) and rate-dependent ( ) parts, where:

and, in order to satisfy (18), we assume in what follows that:

Using the results obtained so far and assuming that m = 0, we write the microforce balance (7) as:

where 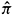is given by

The distinction between (22)₁ and (22)₂ is very important: the first is a restriction on the manner in which microstructural changes may occur; the second is an identity that defines p when there are no microstructural changes, which implies that the microforce balance is automatically satisfied.

4 Special theory

We may interpret the microstructural field a as the cohesion variable: it varies from 1 (pristine material) to 0 (cracked-up material). In the continuum damage mechanics literature (1 - a) is called the damage variable. If 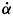> 0 (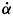 < 0) in a given material point, its cohesion is undergoing a positive (negative) growth.

Now, we specialize the theory by assuming that the free energy response is given by:

where is the strain energy response, which is such that (F, 0) = 0, (I, a) = 0 and:

The function represents the cohesion energy response and the gradient energy response is assumed to be given by:

where k > 0 is a material constant.

As we already remarked, the microforce balance restricts the manner in which microstructural changes occur (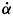¹ 0). Thus, in the current context, microstructural changes (equation (22)₁) are restricted by:

where:

From the above definition and the constitutive assumptions made so far(A⁺> 0, A^-< 0), we can observe that R^-> R⁺.

Equation (27)₁ implies that:

is a necessary condition for positive cohesion growth, whereas equation (27)₂ implies that:

is a necessary condition for negative cohesion growth.

It is somewhat illuminating to interpret the first term of right hand side of (28). It measures the difference between the cohesion variable at a point and its mean value at neighboring points. It is positive (negative) if this difference is negative (positive).

4.1 Kinetic equation and elastic range

Now, we assume that both (29) and (30) are also sufficient conditions for microstructural changes. Thus,

Therefore, from (27), we write the kinetic law for a as:

Equations (32)₁ and (32)₃ correspond to positive (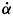 > 0) and negative ( 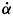< 0) cohesion growth, respectively. Equation (32)₂ corresponds to situations where the cohesion state is frozen in. In this case, no microstructural changes occur and the material behaves elastically. Thus, we define the Elastic Range as the set of all F , for a fixed (a, p, Da), such that:

4.2 Damage healing and irreversibility

By damage healing we mean a positive cohesion growth. This very interesting effect is exhibited by certain materials (see for instance White et al (2001)). As already discussed, a necessary and sufficient condition for damage healing is given by (29):

where we may interpret

as the damage healing driving force.

We see that both first and second terms of the right hand side of the above equation favour damage healing only when: Da > 0, which means that in comparison with the point in question the cohesion of neighboring points are higher; f'(a) < 0, which means that, from the energetic point of view, the material point prefers the virgin state. On the other hand, the third term never favours damage healing because A⁺> 0. Also, from (25), we see that t > 0 always opposes damage healing.

Let us assume that, for a fixed (F, p, Da), R⁺ is a nondecreasing function of a. In this case, the condition R⁺ < 0 means that damage healing is impossible even if t = 0. Also, let us write the condition (34) in terms of a. For this, we first define for a fixed (F, p, Da), the critical value of a - a_H - as the solution, if it exists, of the equation R⁺(F,a_H, p, Da) = 0. Then, we conclude that damage healing is impossible whenever a < a_H.

4.3 Damage nucleation, growth and failure criterion

As we already discussed, a necessary and sufficient condition for negative cohesion growth is given by (30):

where we interpret:

as the resistance against decohesion. We see that both first and third terms of the right hand side of the above equation oppose damage growth only when: Da > 0, which means that in comparison with the point in question the cohesion of neighboring points are higher; f'(a) < 0, which means, from the energetic point of view, that the material point prefers the virgin state. Also, the third term always opposes damage growth because A^-< 0. Also, from (25), we see that t > 0 drives the decohesion process.

Let us assume that, for a fixed (F, p, Da), R^- is a nondecreasing function of a. This means that, in a given material point, the resistance can not decrease if the cohesion increases. In this case, we discuss a special case under which negative cohesion growth is always possible. This case is given by the condition R^- < 0, which means that damage grows without resistance even if t = 0. For this reason, we interpret this condition as a failure criterion. It is convenient to write the condition (36) in terms of a. For this, we first define for a fixed (F, p, Da), the critical value of a - a_C - as the solution, if it exists, of the equation

R^-(F, a_C, p, Da) = 0 .

Therefore, we conclude that damage grows without resistance whenever a < a_C.

It is convenient to split the negative cohesion growth into damage nucleation and damage growth. By damage nucleation we mean a negative cohesion growth in the special case where, at a point, a = 1, Da = 0 and p = 0. Otherwise, we have damage growth. Thus, damage nucleation takes place whenever:

t(F, 1) > Y₁ : = -f'(1) - A^-(F, 1, 0),

where Y₁ is the damage nucleation threshold. On the other hand, damage growth takes place whenever:

t(F, a) > Y₂ : = kDa - f'(a) - A^-(s),

where Y₂ is the damage growth threshold.

Finally, we remark that the damage resistance function R^- is analogous to the R-curve in fracture mechanics. Its dependence on F allows the damage resistance to be strain dependent. In particular, different tensile and compressive responses can be described.

5 Example: Mullins effect

As an application of the modelling framework developed in this paper, we present in this section some qualitative results related to the stress-softening phenomenon (Mullins effect) as is outlined by Krishnaswamy and Beatty (2000).

We consider an uniaxial extension described by:

where x_i and X_I are the cartesian coordinates of x and X (equation (1)), and l and d are positive constants.

The principal invariants of the right Cauchy-Green strain tensor C = F^T F are:

To model certain foamed rubbers Krishnaswamy and Beatty (2000) use the following strain energy function for the pristine material:

where m₀ is a positive material constant. By assuming that the strain energy response is

it follows from equation (25) that

and, by equation (15), that the components of first Piola-Kirchhoff stress S, which is given by

are S_ij = 0 for i ¹ j, and

In the case of an uniaxial stress state, where S₁₁ = S and S₂₂ = S₃₃ = 0, we have that

whereas the corresponding component of the Cauchy stress is

We also assume that gradient effects are negligible, which means that k: = 0 in equation (26), and that the cohesion energy (24) is given by:

where b > 0 is a material parameter. We choose a simple constitutive function for B⁺ and B^- in equation (20):

where b > 0 is the kinetic modulus. We also choose in equation (20) the following constitutive functions:

where, by (21), c > 0, a_T < 0 and a_C < 0. Notice that, as we already remarked, A⁺ is a parameter associated with damage healing. In order to preclude this effect it is enough to assign a large value to c, otherwise, if we consider damage healing we choose a small enough value to c. The constitutive choice for A^- allows us to consider different resistances to traction (a_T) and compression (a_C).

Taking into account the aforementioned constitutive assumptions, the equation (32) is now written as:

where:

Equation (49), which is a rate-dependent kinetic law for a, is similar to the viscoplastic regularization of the Perzyna type (see Simo and Hughes (1999)), in which the rate-independent law is recovered by taking b ® 0.

Let us define the normalized quantities:

H* = where H = T, S, t, b, c, a_T, a_C and b* - b m₀

We consider initially the cyclic loading shown in Figure 1. Figure 2 shows the normalized Cauchy stress T^* versus the stretch l with the parameters:

b^* = 0.4, = = 0, c^* = 10⁵

(which means that there is not damage healing) and b^* = 0.005 s^-1 (which means that this case is rate-independent). Observe that this curve is very close to the one obtained by Krishnaswamy and Beatty (2000).

It is interesting to observe the same situation in a rate-dependent model, by using b^* = 0.5 s^-1. Figure 3 shows the response for this case.

Now we consider the loading shown in Figure 4.

Figure 5 shows the normalized Cauchy stress T^* versus the stretch l with the parameters: b^* = 0.4, = = 0, c^* = 10⁵ (without damage healing) and c^* = 0.8 (with damage healing), and b^* = 0.005 s^-1 (rate-independent case). Observe that during the stretch growth both cases (with and without damage healing) have the same result. During the unloading damage healing occurs and the results are different. The damage healing is better viewed in Figure 6 where the damage variable increases during the unloading.

We show in Figure 8 different tensile and compressive responses under the loading history shown in Figure 7. In this case we use the following parameters:

b^* = 0.4, = -0.1, = -1.0, c^* = 10⁵

(without damage healing) and b^* = 0.005 s^-1 (rate-independent case).

6 Conclusions

We have proposed a finite strain continuum theory to describe the behavior of elastic-brittle solids with microstructure. The microstructure was described by a single scalar microstructural field. A system of microforces, dual to the microstructural field, was axiomatically introduced. The corresponding balance, augmented with suitable constitutive information, yielded a kinetic equation for the microstructural field, criteria for damage nucleation, growth and healing as well as a failure criterion based on attainment of a critical value of the microstructural field. The potentiality of the theory was addressed by applying it to the description of the Mullins effect.

Acknowledgements

The support of this research by the CNPq and CTPETRO/CNPq (466146/00) (F.P. Duda) and by the FAPERJ (A.C. Souza) is gratefully acknowledged.

Received: 12/V/03. Accepted: 29/IV/04.

#579/03.

• [1] I.S. Aranson, V.A. Kalatsky and V.M. Vinokur, Continuum Field Description of Crack Propagation, Phys. Rev. Lett. 85 (2000), 118-121.
• [2] M.F. Beatty and S. Krishnaswamy, The Mullins effect in equibiaxial deformation, J. Appl. Math. Phys. (ZAMP), 51 (2000), 984-1015.
• [3] B.D. Coleman and W. Noll, The thermodynamics of elastic materials with heat conduction and viscosity, Arch. Rational Mech. and Analysis, 13 (1963), 167-178.
• [4] H. Costa Mattos and R. Sampaio, Analysis of the fracture of brittle elastic materials using a continuum damage model, Structural Eng. Mech. 3 (1995), 411-427.
• [5] A. DeSimone, J.J. Marigo and L. Teresi, A damage mechanics approach to stress softening and its application to rubber, Eur. J. Mech. A/Solids, 20 (2001), 873-892.
• [6] M. Frémond and B. Nedjar, Damange, gradient of damage and principles of virtual power, Int. J. Solids Structures, 33 (8) (1996), 1083-1103.
• [7] E. Fried and M.E. Gurtin, Dynamic solid-solid transition with phase characterized by an order parameter, Physica D, 72 (1994), 287-308.
• [8] M.E. Gurtin, Generalized Ginzburg-Landau and Cahn-Hilliard equations based on a microforce balance, Physica D, 92 (1996), 178-192.
• [9] M.E. Gurtin, An Introduction to Continuum Mechanics, Academic Press, New York (1981).
• [10] A. Karma, D.A. Kessler and H. Levine, Phase-field model of mode III dynamic fracture, Phys. Rev. Lett. 87 (4) (2001), 455011-455014.
• [11] S. Krishnaswamy and M.F. Beatty, The Mullins effect in compressible solids, Int. J. Eng. Sci. 38 (2000), 1397-1414.
• [12] K. Ravi-Chandar, Dynamic fracture of nominally brittle materials, Int. J. Fracture, 90 (1998), 83-102.
• [13] J.C. Simo and T.J.R. Hughes, Computational Inelasticity, Springer Verlag, Berlin (1999).
• [14] S.R. White, N.R. Sottos, P.H. Geubelle, J.S. Moore, M.R. Kester, S.R. Sriram, E.N. Brown and S. Viswanathan, Autonomic healing of polymer composites, Nature, 409 (2001),794-797.

1

Inertia forces are included in

b.

2

We remark that by definition,

_d and

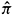have the same properties as far as their dependence on (s,

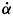) is concerned.

Publication Dates

• Publication in this collection
  11 July 2005
• Date of issue
  Dec 2004

History

• Accepted
  29 Apr 2004
• Received
  12 May 2003