Electromagnetism in a nonsymmetric theory of gravitation

Electromagnetism in a nonsymmetric theory of gravitation

S. Ragusa and D. Bosquetti

Departamento de Física e Informática,

Instituto de Física de São Carlos,

Universidade de São Paulo, C.P. 369,

13560-250 São Carlos, SP, Brazil

e-mail: [e-mail]

Received 29 March, 2000. Revised version received on 5 June, 2000

The field equations of a proposed nonsymmetric theory of gravitation are derived when electro-magnetic fields are present, by adopting a nonminimal coupling which ensures the validity of the equivalence principle. The static and spherically symmetric solution of the field of a charged point particle is obtained.

I Introduction

In a previous work [1] a theory of gravitation based on a nonsymmetric metric was formulated (pure gravitation with no association of the antisymmetric part of the metric to the electromagnetic field strength). The sources of the metric field are the matter energy-momentum tensor T_mn and the matter fermionic particle number current density S^m . This is a conserved current with particle number fermionic charge F = ò S⁰d⁴x , a constant which measures the coupling of the current to the geeometry. The theory was shown to be free of non-physical radiative negative-energy modes even when it is expanded about a Riemannian background, being outside of the class of ill-behaved nonsymmetric theories analyzed by Damour, Deser and McCarthy [2]. Only the symmetric part of the connection is present in the field equations, making the theory as close as possible to general relativity. A solution of the field equations for a spherically neutral point particle has been obtained [3], together with its implications for the motion of light and test particles. The theory is shown [3] to be consistent with all four general relativity solar tests. In the following we shall study the field equations when electromagnetic fields are present. The electromagnetic field Lagrangian that we shall use is the one given by Mann, Palmer and Moffat [4], which rescues the validity of the weak equivalence principle, which Will [5] showed to be violated if only a minimal electromagnetic coupling (same form as in general relativity) were adopted. This is because with such a minimal coupling the gravitational acceleration a of an electrically neutral body of total mass m composed of charged particles turns out to depend on its internal electrostatic energy E_e . Spedifically, the accelaration is related to the one of gravity g by [6] a = g ( 1 + hE_e/mc² ), where h depends on the metric coeficcients. Will then shows that in the case of a nonsymmetric theory with a minimal electromagnetic coupling h is not zero. With the coupling proposed by Mann et al, as written in Eq. (1) below, h turns out to be null, ensuring then the equivalence principle. The field equations contain one free parameter, Z . However, the solution of the field equations for a static and spherically symmetric field turns out to be independent of Z .

In Sec. II we establish the expression of the gravitationally modified Maxwell inhomogeneous equation and of the electromagnetic energy-momentum-stress tensor. In Sec. III we display the field equations of the theory when the electromagnetic field is present and in Sec. IV we determine the solution of the coupled field equations for the case of a static and spherically symmetric point particle. We draw our conclusions in Sec. V.

II The electromagnetic field equations

Mann et al [4] write the electromagnetic Lagrangian density L_em = L_em with

where, as usual, F_mn = A_n,m-A_m,n is the electromagnetic field strength tensor and

The matrix g^mn is the inverse of the nonsymmetric gravitational field g_mn defined by

g = detg_mn and g_s = detg_(mn) . The minimal coupling would correspond to have f and Z both equal to one. Equation (2) can also be written as

where round (square) brackets stand for symmetric (antisymmetric) part.

Varying the Lagrangian density with respect with respect to A_m of the field plus the interaction Lagrangian density, L_em = -J^mA_m , we get, using Eq. (4)

which is the inhomogeneous Maxwell equation in the presence of the nonsymmetric field. Next we consider the variation with respect to g^mn . We get

where

is the energy-momentum tensor of the electromagnetic field. This is a traceless tensor, g^maE_ma = 0 , because we have the relation

This can be proved by direct calculation from the relations g^-1 = e_abgdg^0ag^1bg^2gg^3d and = e_abgdg^(0a)g^(1b)g^(2g)g^(3d) , or from the relations g = e^abgdg_0ag_1bg_2gg_3d and g_s = e^abgdg_(0a)g_(1b)g_(2g)g_(3d) together with g^mn( ¶g_rs/¶g^mn) = -g_rs (to obtain this last relation just write its right hand side as ag_rs and then contract with g^rs to obtain a = -1 ).

III The gravitational field equations

When the electromagnetic field is present, the gravitational field equations of the theory [1] become

where T^¢_mn = T_mn-(1/2)g_mnT with T = g^abT_ab, c.p. stand for the cyclic permutation of the indices m,n and a, L is the cosmological constant and

involving only the symmetric part of the connection, is the analogue of the Riemannian Ricci tensor, and

Since at infinity the field of localized matter tends to that of flat space-time, g^[mn] as well as g_[mn] must satisfy the boundary condition of vanishing at infinity.

We also have the relation

where s_mn , symmetric and with determinant s , is the inverse of g^(mn) , defined by g^(mn)s_ma = d_aⁿ .

It is to be noted that T_mn , defined [1] by dL_m = (/2)dg^mnT_mn where L_m is the matter Lagrangian density, is related to the contravariant matter tensor T^mn , defined by L_m = -()/2)dg_abT^ab as in general relativity, by[1]

This follows from the relation d g_ab = -dg^mng_mbg_an , resulting from the variation of Eq. (3). Therefore, T_mn will have a symmetric and an antisymetric part even for a symmetric T^ab .

IV The field of a charged point particle

The static and spherically symmetric metric tensor in spherical polar coordinates is of the form

and all other components equal to zero. The non-zero elements components of the inverse matrix are

Outside the source, in vacuum, the solution of Eq. (12) is [3], for m = 0 , wr²(ag-w²)-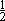 = F , where F is the conserved number fermionic charge . Then,

As g = (w²-ag)r⁴sin²Q and g_s = -agr⁴sin²Q, we get from Eq. (2),

The second way of writing the value of f makes it easier the calculation of its g^mn -derivatives. The electric field is E(r) = F₀₁ . Now, outside the source Eq. (5) yields, for m = 0 ,

independently of Z . Upon integration we get

where the constant of integration has been put equal to the charge Q of the particle to reproduce the usual Reissner-Nordström (RN) result when F = 0, which implies, from Eq. (27) below, ag = 1 . From Eqs. (7), (18) and (20) we obtain the following non-zero components of E_mn:

We see that the energy-momentum tensor is independent of Z and, therefore, the same will occur for the gravitational field equations.

From now on the calculation proceeds as in Ref. [3]. From Eqs. (15) and (25) we see that Eq. (10) is identically satisfied. From Eqs. (9) and (22) we obtain aU₀₀ + gU₁₁ = 0, as in Ref. [3]. It then follows the same relation

derived in [3], which integrates to

Recalling Eq. (17) we then obtain

From now one we shall neglected the small contribution of the cosmological constant in Eq. (9). The U₂₂ equation gives, after using Eqs. (23) and (17),

Using Eq. (26) we get

Choosing the constant of integration in such a way that the RN result is obtained when F = 0 , we get

where m is the mass of the charged particle and

which goes to -r^-1 when F vanishes. Then, from Eq. (27) we obtain

Equation (32) can be put in closed form:

with the term -p/2 to give the right limit, -r^-1, when F vanishes.

The electric field is, from Eqs. (20) and (27),

At large distances,

r >> |

F |

,

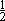
E(

r) goes into the RN Coulomb field but for small values of

r , it behaves as

r

^-1 .

V Conclusions

By adopting a nonminimal coupling that ensures the validity of the equivalence principle we have derived the field equations of a proposed nonsymmetric theory of gravitation [1] when electromagnetic fields are present. The nonminimal coupling contains one free parameter, Z . However, it is shown that for a static spherically symmetric field the electromagnetic field equations and the energy-momentum-stress tensor are independent of Z . Therefore, from this last fact, it follows that the same will occur for the gravitational field equations. The solution of the field equations for the case of charged point particle is obtained. Apart from de strong deviation of the metric tensor from the usual Reissner-Nordström (RN) solution, the electric field departs strongly from the Coulomb field value obtained in the RN case, to which it approaches only at large distances. At small distances it behaves as r^-1.

• [1] S. Ragusa, Phys. Rev. D 56, 864 (1997).
• [2] T. Damour, S. Deser and J. McCarthy, Phys. Rev. D 47, 1541 (1993).
• [3] S. Ragusa, Gen. Relat. Gravit. 31, 1 (1999).
• [4] R. B.Mann, J. H. Palmer and J. W. Moffat, Phys. Rev. Lett. 62, 2765 (1989).
• [5] C. M. Will, Phys. Rev. Lett. 62, 369 (1989).
• [6] A. P. Lightman and D. L. Lee, Phys. Rev. D 8, 364 (1973).

Publication Dates

• Publication in this collection
  11 Jan 2002
• Date of issue
  2000

History

• Received
  29 Mar 2000
• Reviewed
  05 June 2000