SQUIDs and inverse problem techniques in nondestructive evaluation of metals

SQUIDs and inverse problem techniques in nondestructive evaluation of metals

A. C. Bruno

Departamento de Física, Pontifícia Universidade Católica do Rio de Janeiro

Rua Marquês de São Vicente 225, Rio de Janeiro, RJ 22453-900 Brazil

Received on 3 July, 2001

Superconducting Quantum Interference Devices coupled to gradiometers were used to detect flaws in metals. We detected flaws in aluminum samples carrying current, measuring fields at lift-off distances up to one order of magnitude larger than the size of the flaw. Configured as a susceptometer we detected surface-braking flaws in steel samples, measuring the distortion on the applied magnetic field. We also used spatial filtering techniques to enhance the visualization of the magnetic field due to the flaws. In order to assess its severity, we used the generalized inverse method and singular value decomposition to reconstruct small spherical inclusions in steel. In addition, finite elements and optimization techniques were used to image complex shaped flaws.

I Introduction

Nondestructive Evaluation (NDE) consists in the development of measurement technologies and analysis techniques for the quantitative characterization of materials and components by a noninvasive way. It aims to assess the integrity, properties and composition; and to measure geometrical features such as flaws and other imperfections. NDE is used in process control, in production quality control, and in components, which are already in use. NDE enjoys also an increasingly important role in both: the development and the understanding of new materials. Its goals are improving the quality and cost effectiveness of producing these materials, and perhaps what is more important, extending the useful lifetime of components and structures fabricated by them. At present, many efforts are intended to develop and perfect techniques that are capable of monitoring and controlling the amount and rate of material degradation during in-service life, which has been accomplished, using advanced sensors along with data processing and imaging techniques.

Among the several NDE techniques available [1], we focused our efforts on electromagnetic NDE that consists basically in applying current or magnetic field to a sample and measuring the response. We used SQUIDs (Superconducting QUantum Interference Devices) and inverse problem techniques, for measuring and sizing flaws in metal samples. Conventional technology, in many situations, lacks adequate sensitivity, spatial resolution, dynamic range and frequency response; the SQUID deals with all those problems with unequalled skill. In order to provide quantitative images comparable to the ones obtained by other NDE techniques such as ultrasound, x-ray or thermal imaging, we applied inverse problem algorithms, to obtain two and three-dimensional images of flaws in the samples under test.

We first described a home made SQUID as part of a NDE system set up to measure flaws in aluminum samples. In order to better visualize the measurements we implemented two-dimensional spatial filters to process the data. Next, a SQUID susceptometer is presented and tested to detect flaws on steel samples. With the purpose of imaging the flawed samples, inverse problem techniques are introduced and tested with simulations and actual measurements.

II The wire-junction SQUID

The SQUID is the most sensitive device known for the measurement of magnetic flux. It can be built basically from a superconducting ring closed by a Josephson junction. There are two types of SQUIDs. The RF SQUID has one Josephson junction and the DC SQUID has two Josephson junctions in parallel. Its operation is based on two phenomena that occur when the material the SQUID is made of becomes superconduting: flux quantization and the Josephson effect. Flux quantization dictates that the flux inside the SQUID ring cannot change continuously, but only in multiples of F₀, the flux quantum (F₀ = h/2e = 2.07 ×10^-15 Tesla- m²). The Josephson effect states that a superconducting current can cross the Josephson junction, which consists of a weak link between two superconductors, up to a limit known as the critical current. These properties cause the SQUID impedance to be a periodic function of the magnetic flux threading the SQUID. The net result is that the SQUID works as a flux-to-voltage converter with unparalleled sensitivity. In order to become superconducting, conventional SQUIDs, made of niobium, must be immersed in liquid helium.

Our niobium two-hole RF SQUID [2], developed in collaboration with James E. Zimmerman from NIST, is radio frequency biased, through a resonant circuit, by means of a room temperature current source. The resonant circuit is coupled to the SQUID by inserting its inductor element in one of the SQUID holes, as depicted in Fig. 1. A key advantage of our SQUID is the Josephson junction design. It is made of two niobium 0.4 mm wire segments, one flat on the end and one pointed, pushed against each other, as shown schematically in Fig. 1b. Due to its extremely high sensitivity, the SQUID is not used directly to measure magnetic fields. Rather, it is encapsulated in a superconducting shield, with the magnetic signal coupled to it by a flux transformer. The flux transformer consists of a primary coil wound in a differential configuration and a secondary coil coupled to the SQUID, by inserting it in the other SQUID hole, as shown in Fig. 1. This secondary coil is inside the shield and the primary coil is placed at the position where the magnetic field should be measured. When the external magnetic field induces current in the primary coil, this current generates a magnetic field in the SQUID through the secondary coil. We used the primary coil in a configuration known as an axial second order gradiometer. An axial gradiometer consists of coaxial coils connected in series with specific number of turns with appropriate polarity, and separated by distances called baselines, as shown schematically in Fig. 1a.

Figure 1.
(a) Schematic drawing of an RF-SQUID coupled to a flux transformer. The primary coil is configured as a second order gradiometer. (b) Top view of the RF-SQUID sensor showing the wire-junction design.

In a first approximation, it works as a spatial discriminator, favoring the detection of fields from near sources against fields from distant ones. With the purpose of dealing with all kinds of gradiometer designs, in a quantitative way, we developed a one-dimensional model for the gradiometer based on spatial filtering techniques [3, 4]. This model is valid if the field is approximately constant over the gradiometer area. Later on, E. Andrade Lima et al. [5, 6] developed a general two-dimensional model, where this restriction was removed. The model is not dependent on any particular field source; it relies only on the geometrical features of the gradiometer such as coil area and shape, and the baseline. It can be used to simulate any gradiometer response, perform gradiometer analysis and design, and for calibration.

Our SQUID gradiometer has 15 mm diameter coils, 40 mm baseline and achieves a 50 ×10^-15 Tesla/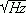 sensitivity down to 0.1 Hz. More sophisticated systems, using a DC SQUID, can be one order of magnitude more sensitive. Due to its high sensitivity, and to the discovery of new materials, to which superconductivity occurs at liquid nitrogen temperatures, SQUID systems open new frontiers for nondestructive evaluation of electrically conducting and also ferromagnetic materials.

III Electric current injection method

The Electric Current Injection (ECI) method is used in materials where the electrical conductivity due to the flaw differs significantly from the conductivity of the bulk material. This method is applicable to regularly shaped objects, made of materials that are electrically conductive but not magnetically permeable. The ECI method is carried out by injecting current between two points of the test sample and detecting the associated magnetic field. For practical values of applied electric current in metals, the strengths of the associated magnetic field and of the field distortion due to the flaw are orders of magnitude smaller than the earth's field. For instance, a sizable 10 mm hole through a conductive plate carrying a 10 A current generates a peak field distortion of about 0.5 mT at 10 mm distance. A high sensitivity is needed when the probe cannot be placed at close proximity to the sample under test or when searching for a smaller defect.

In order to test the feasibility of using the SQUID as a part of an ECI system [7], we measured several aluminum samples with dimensions 1 m × 1 m × 1 mm, with single circular holes with diameters ranging from 2 mm to 8 mm. A current was applied to the ends of the plates with amplitudes varying from 100 mA to 5 A. The measurements were taken by moving the plate under the SQUID system in two orthogonal directions. Very often, the actual sample to be inspected may not be accessible, so, we used lift off distances much larger than the hole diameters. In this situation the field distortion due to the flaws were immersed in the magnetic field generated by the finite plate itself.

Fig. 2a is a contour plot representation of the measured field at a 90 mm lift-off, due to a plate carrying a 5 A current and an 8 mm flaw. A slight distortion of the contour lines, due to the flaw, can be seen over the hole position along the x direction at y = 100 mm. Fig. 2b shows a characteristic dipolar pattern due to the flaw, as a result of processing the signal in Fig. 2a with a high-pass spatial filtering algorithm developed by C. Hall Barbosa et al. [8]. A spatial filter is a processing technique applied to signals that vary in space, analogous to the conventional filtering techniques that are applied to time varying signals. The implemented algorithm is based on spatial operations performed on local neighbors of every input flux value. Each point is replaced by a weighed average of its neighbors. This can be done, by convolving the magnetic flux with a spatial mask that defines the finite impulse response filter weights [9]:

where f_i (m, n) and f₀ (m, n) are the input and output flux of the spatial filter, respectively, W is the window defining the spatial mask and w(k, l) are the filter weights given by the matrix below:

Figure 2.
(a) Contour plot representation of B_z measured at a distance of 90 mm from an 1 m × 1 m × 1 mm aluminum plate carrying 5 A current, with an 8 mm hole centered at x = 90 mm and y = 100 mm. (b) Contour plot representation after application of the spatial filter algorithm, where the dipolar pattern can be observed. The × mark indicates the center of the hole and the dotted lines in the contour plot represent negative field values.

The algorithm was implemented with a technique known as unsharp-masking, which consists in filtering the image with a high order low-pass filter, as the one represented by the matrix above, and then subtracting the result from the original image.

IV Magnetic field perturbation method

This method is used to detect flaws in ferromagnetic materials where the flaw permeability differs significantly from the one of the bulk sample. Consider a uniform steel plate placed perpendicularly to the axis of a magnetizing coil. It can be shown that, at the center of the coil, the field lines are perpendicular to the plate surface [10]. If we scan a magnetometer over the plate and a surface-breaking flaw is present, the field will be distorted in this region due to the discontinuity in the magnetic permeability. The field distortion will be proportional to the volume of the flaw to a certain depth. Because of the resulting shielding of magnetic fields, just a small amount of the applied field penetrates deeply into the sample, thus making the field perturbations from deep flaws difficult to be detected.

We used a SQUID susceptometer system, custom-made by Conductus, Inc., in collaboration with John P. Wikswo, Jr. at Vanderbilt University, to measure flawed plates and pipes [11, 12]. The system consists of DC SQUIDs coupled to five first-order axial gradiometers and a magnetometer, all capable of being used in conjunction with three superconducting magnets. The gradiometer used for these measurements has 3 mm diameter coils with 8 turns, a 40 mm baseline and a sensitivity of 100 pT/

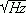. A static magnetic field of up to 100 mT can be generated at the sample site by a 38 mm long magnet with a 24 mm diameter that is concentric with the gradiometer.

The test samples consist of low carbon steel plates 150 × 120 × 13 mm placed about 3 mm below the pick-up coils. In this case we placed the SQUID system close to the sample due to the proximity of the sample borders. A pattern of four flaws at the vertices of a 20 mm square was drilled in the steel surface, with the flaws having several depths. Each flaw consists of a blind hole machined with drill bits having a 45^° angle tip, with diameters ranging from 5 mm to 0.8 mm and depths from 5 mm to 0.3 mm.

A very high system stability was observed, as an apparently unflawed plate is scanned by the system. The measurements were made inside a magnetic shield enclosure. The main source of noise was the small vibrations of the sample due to the movement of the x-y scanning stage in the presence of the applied field.

Applying the field perpendicular to the sample makes this technique more suitable for detecting surface-breaking flaws. If the field is applied parallel to the sample, superficial flaws will be difficult to detect if the sensor sensitivity stays the same. As an example, Fig. 3a shows a wire-mesh representation of the normal component of the magnetic detected by the SQUID, due to a 100 mT field applied parallel to the surface of the test sample. From left to right, the upper flaws have a diameter of 5 mm and depths of 2.5 mm and 4 mm respectively. The lower flaws have a diameter of 1.5 mm and depths of 4 mm and 2 mm respectively. Notice that only the dips corresponding to the upper flaws are visible. The field ramp is caused by a misalignment between the surface of the sample and the plane of the gradiometer coil. When only 10 mT is applied perpendicular to the sample, the distortions due to all 4 flaws can be visualized as seen in Fig. 3b. The different pattern for the upper ones represents multiple resets in the SQUID electronics due to the amount of field distortion, which reflects the large size of these two flaws for this particular susceptometer sensitivity range; the resets could have been avoided by reducing the SQUID sensitivity, but then the small flaws might have been missed.

Figure 3.
(a) Wire-mesh visualization of the magnetic field Bz detected by the SQUID scanning a steel sample having four flaws. The two dips are due to the upper flaws when an 100 mT field is applied parallel to the sample surface. (b) Applying a magnetic field ten times smaller perpendicular to the sample allow us to see all four flaws.

V Forward problem for simple flaws

Once the magnetic field associated to a flaw is detected, there remains the problem of how to estimate its geometrical shape. One option can be the use of neural networks to associate a magnetic field pattern with the flaw geometry [13]. Another approach is to solve the so called inverse problem. The first step in solving the inverse problem is to design a forward problem, which consists in finding a suitable model that contains the flaw characteristics we are interested. Simple flaws that can be restricted to straight-line voids, when the two surfaces are close together, such as small inclusions or cracks, can be modeled by positioning magnetic dipoles in the region of the flaw. This is based on the fact that a flaw has boundary surfaces, which reduces the flux density in the material when it is magnetized. Magnetostatic theory shows that some magnetic dipole sources exist at such boundary surfaces, pointing in the opposite direction of the applied field. The magnetic field due to a dipole can be obtained from the gradient of the magnetic scalar potential [14]:

where m₀ is the permeability of the free space, r is the measurement position, r₀ is the dipole position and m the dipole magnetic moment. The normal component of the magnetic field b_z measured at position (x, y, z) for a dipole located at position (x₀, y₀, z₀), and pointing in the x direction, can be written as:

The description of the dipole model above, disregards the bulk magnetization of the sample, so this expression accounts only for the field generated by the flaw.

VI Inverse problem for simple flaws

In such case, an analytical inverse solution is possible. Once the magnetic field is obtained, the strength of the magnetic dipole m_x can be found, using the inverse procedure explained below. The strength will be point wise proportional to the difference between the normal components of the magnetic field intensity in the adjoining media. Similar inverse problems also exist in other areas such as biomagnetism [15], geomagnetism [16], and electrical impedance tomography [17] and a number of different approaches have been used to solve them [18-21]. Although knowing that in general, this problem has no unique solution, it was shown that it is possible to find a best estimate for the inverse solution, using adequate a priori information and, constraining the possible solutions to predetermined source configurations suited for each specific problem [22, 23].

We applied the so-called truncated generalized inverse or minimum-norm least-squares estimation [24, 25], where the chosen solution minimizes the squared difference between the measured field and the field generated by the estimated source distribution. It also has the property of minimum norm solution, as compared to all other possible solutions, which means that the solution found would be the one with minimal energy. In order to test feasibility of this approach, we will simulate the measurement of a structure consisting of a permeable bar with a constant permeability m, containing flaws in the shape of spherical inclusions of radius r. It has a thickness t, width w, and length l. Its cross sectional plane is located between the x coordinates - w/2 and + w/2 and between the z coordinates -t and 0, as shown in Fig. 4.

Figure 4.
Permeable bar with thickness t, width w, and length l. An external magnetic field is applied along the x direction. The inverse solution will be seek on a series of planes, each one consisting of a regularly spaced grid of N_d magnetic dipoles pointing against the externally applied field as illustrated above.

The search for possible solutions was confined to a set of zx planes containing a regularly spaced N × N grid of magnetic dipoles with unknown strengths. The orientation of the dipoles in the solution plane is fixed along the -x direction, since the applied field H_a is along the +x direction and the field is detected perpendicularly to the top of the bar.

By obtaining the strengths for each grid position of the recovery dipoles, it is possible to locate the flaw, and estimate its spatial distribution, i.e., positions where the dipole strengths are greater than zero. Assuming that the normal component of the field is measured at N_p positions, we will represent it by an N_p × 1 vector b_z. The N × N recovery dipole grid will be represented by an N_d × 1 vector m. Thus, the field vector b_z due to the flaw, can be written as a linear function of the unknown recovery dipoles strength vector m:

where L is the (N_p × N_d) geometric or lead-field matrix. From the forward solution stated in eq. (3) each element of L is given by:

where (x_i, y_i, z_i) are the measurement positions, (x_j, y_j, z_j) the recovery dipole positions, i = 1, ..., N_p and j = 1, ..., N_d.

We will consider here cases where N_p > N_d, as this is the usual situation found in real measurements, i.e., more measurement positions than dipoles in the recovery model. In this case, only an approximate solution can be found. Nevertheless, the generalized inverse allows us to obtain a best estimation of m, denoted by m^*. This estimate will minimize the norm of the residual error ||e||:

Multiplying both sides of (4) by L^T the transpose of matrix L, the expression for the minimization of the residual error norm is:

However, due to imprecision in the measurements, the square matrix L^TL can be singular and a unique solution of the form:

cannot be obtained. Through the application of the generalized inverse technique, it is still possible to find the best estimate of the dipole distribution applying the singular value decomposition on the lead-field matrix L, yielding to the following product of matrices:

where U is an orthogonal N_p × N_p matrix, V is also an orthogonal N_d × N_d matrix, and S is a diagonal N_p × N_d matrix, whose elements are arranged in a noncrescent order. The nonzero elements of S are called the singular values of L. Substituting (9) in (4) and applying the definition of the generalized inverse, the approximate solution is given by:

Two different distributions of spherical inclusions inside the permeable bar were simulated. The z component of the field above the sample surface due to an inclusion is given by [26]:

where m₀ is the permeability of the free space, and H_a is the magnetizing field applied along the x direction. We scanned a 1 mm regularly spaced recovery grid with 11 × 11 magnetic dipoles located between -5 mm £ x₀£ 5 mm, and -10 mm £ z₀£ 0 mm through the y axis. The magnetic field produced by one single spherical inclusion, with 1 mm of diameter, centered at x₀ = 0 mm and z₀ = -3 mm, can be seen in Fig. 5a. Figure 5b shows the cross sectional view of the single spherical inclusion at plane y₀ = 0 mm. A uniform magnetic field of 1T was applied to the bar. In the present simulations the bulk field of the material was neglected.

Figure 5.
(a) Normal component of the magnetic field produced by an 1 mm diameter spherical inclusion inside a ferromagnetic structure (m = 1000 H/m) subjected to an external magnetic field of 1T. (b) Illustration of the cross sectional view of a 1 mm diameter spherical inclusion in the bar centered at z₀ = -3 mm and y₀ = 0 mm. (c) Reconstructed image obtained. The grayscale image has been displayed to present maximum dynamic range.

The reconstruction is represented as a gray scale image, where white represents the maximum dipole moment (inclusion) and black represents its minimum. The magnetic image as a result of the reconstruction method applied to the field due to the single inclusion can be seen in Fig. 5c.

In the second simulation, we used a cluster of 13 spherical inclusions with 0.5 mm diameter centered about x₀ = 0 mm and z₀ = -3 mm. The corresponding field is plotted in Fig. 6a. The cross sectional view of the second distribution can be seen in Fig. 6b. Despite the similarities of the detected fields, the technique was able to successfully distinguish between the two distinct inclusion configurations as shown in Fig. 6c. As far as the inclusions located in the lower part of the cluster are concerned, the image reconstructed from the second distribution lacks better resolution. This is because the magnetic field produced by the upper inclusions blinds the inverse technique and the image cannot be reconstructed accurately.

Figure 6.
(a) Normal component of the magnetic field produced by a cluster of 13 spherical inclusions with 0.5 mm diameter inside the permeable bar subjected to an external magnetic field of 1T. (b) Illustration of the cross sectional view of the 13 inclusions inside the bar. (c) Image reconstruction of the cluster of inclusions. The grayscale image has been displayed to present maximum dynamic range.

VII Forward problem for complex flaws

Unfortunately, for flaws with complex geometries and due to nonlinear response of ferromagnetic materials, an analytical approach is seldom used actually. In such case three- dimensional finite-element modeling is essential for precise characterization of large flaws, although there are still many problems to be solved including the hysteresis in the magnetization characteristic of ferromagnetic materials.

We designed our forward problem as a particular case, when the sample is free from electric currents. Thus, we can write Maxwell's equations in our solution space, i.e. the region in space where we want to calculate the magnetic field as:

where, B and H are related by B = mH and m is the permeability of the sample, which in the majority of cases depends on H. Then, a scalar potential y(x,y,z) can be defined, from which the field H is derived through the expression

This definition is valid for any curl free field, so we can rewrite eq. (13) as

which in explicit three-dimensional form is

Our problem resides in solving the above second-order differential equation for y with the appropriate boundary conditions, to take into account the applied field. Once the potential is known, the field generated by the sample with or without flaws, can be obtained using eq. (14). The solution of eq. (16), for most practical geometries, is impossible to be obtained by analytical methods. One of the numerical methods used to solve it, is known as the Finite Element Method. It consists in trying to find an approximation y^* to the potential y which satisfies

in all solution space. Normally, a polynomial approximation is used. Instead of forming a continuous approximation over all the solution space, we can form piecewise approximations that are valid inside each part. In order to do that, the solution space is divided into a number of finite size elements, the finite elements. The polynomial approximation will depend on the shape of the element used. These elements form a mesh over the solution space. It is clear that the smaller these elements or the denser the mesh, the closer the numerical solution will be to the exact one. As a last remark, since the permeability m is not constant, it is necessary to establish an iterative procedure until convergence is obtained. There are a number of software packages available that solve this class of problems and in particular the one stated by eq. (17), for a given solution space geometry [27].

VIII Inverse problem for complex flaws

Our approach to solve the inverse problem associated with complex shaped flaws relies on the use of a finite element procedure to simulate the field due to a mesh in which the coordinates of specific nodes can be altered. The field generated by the model is compared in a least squares sense to the one actually measured due to a flawed sample. If the difference is larger than a threshold the mesh coordinates are altered and the process starts again, until the field generated by the model fits the measured field. This is an ill-posed problem with no unique solution, so we have to make use of a priori information, in order to constrain the possible solutions to a predetermined class of source configurations.

We are particularly interested in studying corrosion pits, which usually start by having a hemispheric shape. To test the inverse procedure, we used the following setup, which half is depicted schematically in Fig.7, where two permanent magnets generate a magnetic field through the plates. Fig. 8 shows an example of a mesh using hexahedral elements generated to simulate the central upper plate in of Fig. 7. Notice that the geometry of the finite elements in the central part of the mesh was chosen to have a circular shape. Choosing the height g^* of the nodes at the circular paths, will allow us to design flaws with circular shapes of various sizes and depths.

Figure 8.
Detail of the finite element mesh used to perform the inverse solution.

Our shape design problem can be stated as: find (g^*₁, g^*₂, g^*₃, ...) such that

where d is a threshold, W is the space where the measurements H_meas. were performed, and (g^*₁,g^*₂,g^*₃,...) is the design-variable vector with the heights of circles in the finite element mesh we are looking for.

The inverse procedure was implemented and tested with experimental data by R. Schifini et al. [28, 29] reproducing the magnetic circuit of Fig.7 containing two ferromagnetic plates (140 × 140 × 6.35 mm) joined by NdFeB magnets with opposite orientations. Point wise Hall magnetic sensors (0.2 × 0.2 mm²) were used to scan the outside surface of the upper plate measuring the tangential component of the magnetic field. Several hemispheroidal pits with different shapes were machined on the sample plate and the inverse procedure carried out. The results obtained show very good agreement with the actual shapes. As an example, Fig. 9a shows the magnetic field measurement due to an 8 mm diameter pit with 2 mm depth, which is shown in Fig. 9b. The measurements were made at a 4 mm distance from a plate. The result of the inverse procedure is shown in Fig. 9c.

Figure 9.
(a) Measured magnetic field perpendicular to the plate using a point wise Hall probe. (b) Detail of the geometry of the fabricated corrosion pit with 8 mm diameter and 2 mm depth. (c) Result of the inverse problem using the finite element approach. .

IX Conclusions

We successfully used SQUID systems to detect circular shaped flaws in aluminum samples carrying currents down to the mA range. Due to the SQUID sensitivity, measurements of millimeter sized flaws could be made at distances 10 times its size. With the system configured as a susceptometer we were able to detect surface-breaking flaws having volumes down to 0.1 mm³ in steel samples, measuring the distortion on the applied magnetic field. Spatial filtering techniques proved to be very useful to extract the signal due to the flaw when the field generated by the sample itself was one order of magnitude higher. To size the detected flaws, we used an inverse problem technique based on the truncated generalized inverse and singular value decomposition to reconstruct simulated spherical inclusions in steel. Finally, using point wise field measurements, finite elements and optimization techniques were used to image complex shaped flaws, such as corrosion pits.

Acknowledgments

I would like to thank CNPq, CT-PETRO, FINEP, PADCT-2, PADCT-3, PETROBRAS and RHAE, for financial support. I thank also the invaluable help of the following undergraduate and graduate students, Carlos Hall, Eduardo Andrade, Guilherme Kühner, Luis Felipe Scavarda, Paula Ornelas and Ricardo Schifini.

• [1] Don E. Bray and Don McBride. Nondestructive Testing Techniques (Wiley, New York, 1992).
• [2] A. C. Bruno and J. E. Zimmerman, Superconducting Devices and Their Applications, p. 240 Springer-Verlag, Berlin (1992).
• [3] A. C. Bruno, P. Costa Ribeiro, J. P. von der Weid and O. G. Symko, J. Appl. Phys. 59, 2584 (1986).
• [4] A. C. Bruno and P. Costa Ribeiro, J. Appl. Phys. 63, 2820 (1988).
• [5] E. Andrade Lima, A. C. Bruno, and J. Szczupak, Supercond. Sci. Technol. 12, 949 (1999).
• [6] E. Andrade Lima and A. C. Bruno, IEEE Trans. Appl. Supercond. 11, 1299 (2001).
• [7] A. C. Bruno, C. Hall Barbosa and L. F. Scavarda, Res. Nondest. Eval. 8, 165 (1996).
• [8] C. Hall Barbosa, A. C. Bruno, L. F. Scavarda, E. Andrade Lima, P. Costa Ribeiro, C. Kelber, IEEE Trans. Appl. Supercond. 5, 2486 (1995).
• [9] A. K. Jain, Fundamentals of Digital Signal Processing, Prentice-Hall, New York (1989).
• [10] A. Cochran, G. B. Donaldson, S. Evanson, R. J. P. Bain, IEE PROC-A 140, 113 (1993).
• [11] A. C. Bruno, A. P. Ewing, J. P. Wikswo, Jr., IEEE Trans. Appl. Supercond. 5, 2482 (1995).
• [12] C. Hall Barbosa, A. C. Bruno, G. S. Kühner, J. P. Wikswo, Jr., A. P. Ewing, Y. P. Ma and C. S. Camerini, Rev. Prog. Quant. Nondest. Eval. 17, 1091 (1998).
• [13] C. H. Barbosa, M. Vellasco, M. A. Pacheco, A. C. Bruno, C. S. Camerini, Rev. Sci. Instrum. 71, 3806 (2000).
• [14] J. R. Reitz, F. J. Milford, and R. W. Christy, Foundations of Electromagnetic Theory (Addison-Wesley, Reading, 1980).
• [15] M. Hämäläinen, T. Hari, R. J. Ilmoniemi, J. Knuutila, O. V. Lounasmaa, Rev. Mod. Phys. 65, 413 (1993).
• [16] D. W. Vasco, Geophys. J. Int. 142, 970 (2000)
• [17] P. Metherall, D. C. Barber, R. H. Smallwood and B. H. Brown, Nature 380, 509 (1996).
• [18] J. G. Berryman and R. V. Kohn, Phys. Rev. Lett. 65, 325 (1990).
• [19] P. Hughett, Ann. Biomed. Eng. 23, 506 (1995).
• [20] S. Tan, N. G. Sepulveda, and J. P. Wikswo, Jr., J. Comput. Phys. 122, 150 (1995).
• [21] O Dorn, H. Bertete-Aguirre and J. G. Berryman, Inv. Prob. 15, 1523 (1999).
• [22] J-Z. Wang, S. J. Williamson, and L. Kaufman, IEEE Trans. Biomed. Eng. 39, 665 (1992).
• [23] N. G. Gençer, Y. Z. Ider, and S. J. Williamson, IEEE Trans. Biomed. Eng. 43, 139 (1996).
• [24] A. C. Bruno, J. App. Phys. 82, 5899 (1997).
• [25] A. C. Bruno, L. Couto Miranda, C. Hall Barbosa, E. Andrade Lima, and G. S. Kühner, IEEE Trans. Mags. 34, 2912 (1998).
• [26] D. E. Bray and R. K. Stanley, Nondestructive Evaluation (McGraw Hill, New York, 1989).
• [27] Opera-3d, Vector Fields Ltd., 24 Bankside, Kidlington, Oxon, OX5 1JE, UK.
• [28] R. Schifini and A. C. Bruno, Rev. Prog. Quant. Nondest. Eval. 19, 897
• [29] A. C. Bruno, R. Schifini, G. S. K.ühner, C. H. Barbosa, J. P. Wikswo, Jr., C. S. Camerini, J. Mag. Mag. Mat. 226, 2061 (2001).

Publication Dates

• Publication in this collection
  23 Apr 2002
• Date of issue
  Dec 2001

History

• Received
  03 July 2001