Comparing the Mori formalism and the green function methods

Comparing the Mori formalism and the green function methods

A.S.T. Pires; M.E. Gouvêa

Departamento de Física, ICEx, Universidade Federal de Minas Gerais, Belo Horizonte, CP 702, MG, 30123-970, Brazil

ABSTRACT

Using a simple model described by a Hamiltonian of fermions coupled to bosons, we show that the relaxation function calculated via a low temperature approximation to the Mori memory function is similar, at least to lowest order, to the relaxation function calculated using a Green function formalism.

The analytical calculation of dynamic properties of many-body systems is, in general, a difficult task to accomplish and most of the theoretical models that have been proposed to take account of this job involve - in despite of the high degree of complexity of the calculations usually required - some approximations and/or are restricted to a limited range of temperatures or wave-vectors. One of the most useful methods for studying the dynamics of a many-particle system is the memory function method proposed by Mori[1] in 1965. That method is based on a generalized Langevin equation, and is a generalization of the projection-operator technique proposed by Zwanzig [2]. Mori's method is physically appealing because it can show how two different time scales, slow and fast, can possibly arise from Hamiltonian systems and how transport coefficients can be related to the interaction energy [1,3]. The method leads to an expression for the Laplace transform of the autocorrelation function in the form of a continued fraction involving static and dynamical quantities. One of the drawbacks of the method is that the related static properties are not calculated as part of the whole procedure but, rather, are assumed to be known from ab initio. However, the main problem of the procedure seems to be the absence of a prescription on how to cut the continued fraction expansion in which the memory function is expanded. Several approximations, or recipes for a reasonable cut, have been proposed in the literature for the calculation of the memory function [3,4], and the relaxation function so obtained has been successfully compared to experimental data [5,6], and to results obtained by using other methods [7]. Although there is a great number of applications of Mori's method, only a few discussions concerning the essence of the method and the validity of the results obtained whit a particular approximation scheme have appeared in the literature [3,8]. A particularly useful approximation to the method, in the low temperature regime, was introduced by some authors [9,10] almost two decades ago; we will refer to this scheme as the low temperature approximation of Mori's method (LTMM). In the LTMM, the memory function, formulated as a relaxation function, is decoupled in the mode-mode approximation. One of the interesting aspects of the approximation is the fact that it yields all frequency moments exact up to first order in temperature.

As it is well known, another very important method to treat low temperature quantum models is the perturbation theory in terms of Green functions [11]. Obviously, each of these two theoretical models, LTMM and Green functions, has its own advantages and drawbacks, and, also, the choice of which method shall be adopted depends, strongly, on the specific features of the problem to be studied. There are, however, some models where these two methods can be applied requiring, basically, the same amount of analytical calculation. Therefore, it is interesting to compare the results obtained by using these two methods.

The aim of this paper is not to propose a new method to treat many-body Hamiltonians, neither to establish limits of validity for each of the two methods discussed here. As we show in the following, these two methods, despite having different characteristics, can lead to the same result. This conclusion is important because it is known how to check the accuracy of a result obtained by using the Green function method up to a certain order: being a perturbative approach, all one has to do is to go one step further obtaining higher order diagrams. However, the LTMM does not have this perturbative character and one of the ways to test its validity is by comparison to other methods: this is what is done in this work.

Our discussion will be based on the results obtained for the following Hamiltonian

For simplicity, we will consider a one-dimensional problem, but the calculations can be easily extended to any number of dimensions. This Hamiltonian can be the prototype for several models. For instance, if a_q is a fermion operator and b_q is a boson operator, Hamiltonian (1) can be used to describe the electron-phonon coupling, as used by Rice and Strässler[12] in their theory for a quasi-one-dimensional band conductor. This same choice for a_q and b_q makes Hamiltonian (1) also suitable to describe a chain of spins with s = 1/2 coupled to phonons, as required for the understanding of the spin-Peierls transition [13]. If a_q and b_q are both boson operators, we can have an exciton-photon system that can be applied, for example, to the study of energy transport by excitons [14]. It is important to notice that our model Hamiltonian does not include terms with four interacting operators.

It is important to emphasize that the discussion done here is not restricted to Hamiltonians as simple as the one defined by (1). In fact, if we wanted to apply one of the two methods, Green function or LTMM, to a more general spin Hamiltonian, the first step would always be to write the operators of that Hamiltonian in terms of creation and annihilation operators. The final product of this procedure, would be a Hamiltonian involving an harmonic part and anharmonic interaction terms - Hamiltonian (1) is just a simple especimen of this kind. More complicated Hamiltonians would require more troublesome calculations, but the kind of conclusion we are looking for in this paper will remain the same.

In order to compare the results obtained by using the LTMM and the Green function methods, we will use these two methods to obtain the relaxation function related to operator b_q. Obviously, the same calculations and conclusions will apply to operator a_q. We start by defining a phonon variable

and calculate the relaxation function given by

using, first, the memory function formalism. In (3), (A(t),B) is the inner product of two operators A and B, defined as

where the brackets á . ñ denote the usual thermal average, and b = 1/k_BT is the Boltzmann factor. In the following, the Boltzmann constant k_B will be taken as equal to 1.

Following Mori's procedure [1,3], the relaxation function is written as

where

is the second frequency moment and S^'(q,w) and S^"(q,w) are, respectively, the real and imaginary parts of the memory function S(q,w), which is the Laplace transform of S(q,t), defined by

In the expressions above, is the time derivative of the f operator

where L is the Liouville operator. The Q operator appearing in the definition of the memory function, Eq. (8), is a projection operator that projects out any terms proportional to f_q and [1,3].

It has to be emphasized that Eq. (5) for the relaxation function is exact. However, the evaluation of the memory function as given by Eq. (8), involves the exp(–iQlQt) term whose exact calculation requires the solution of the the many-body problem directly. Therefore, it is necessary to introduce some degree of approximation at this point. Ayk [9] and Reiter and co-workers[10] proposed an approximation scheme (LTMM) which is correct up to first order in temperature. In their approach, the exponential of Eq. (8), QLQ, is replaced by the normal time evolution operator L giving

The calculation of this approximate expression for the memory function is done according to the following recipe: we start by using the Liouville operator to calculate L²f_q. Then, we expand L²f_q in terms of boson operators retaining, only, the linear and quadratic terms. The operation of Q on this expansion erases the terms linear in f_q. At last, we use the quadratic part of the Hamiltonian to calculate the time evolution and expectation values of the operators.

More insight about the physical meaning of this approximation can be obtained if we take S(q,z), the Laplace transform of the time dependent memory function, and use the following expression

This expression is exact in the frequency space [15]. Here, L(q,z) is given by

Using Eq. (11), we can write

Thus, we see that the replacement QLQ ® L is, in fact, a weak coupling approximation.

Now, we perform the calculation of the relaxation function for Hamiltonian (1) in the LTMM context, following the recipe steps. Using the equation of motion (9), we find, after a straightforward calculation,

Inserting (14) into (10), we find

Using Eq. (4), we finally arrive at

where

In Eq.(17), n_p denotes the usual occupation number. If the operator b_q in Hamiltonian (1) is a boson, n_p = ( – 1)^–1, and if b_q represents a fermion, n_p = ( + 1)^–1.

The calculation of the denominator of (7), (, ), is done by using the identity (, ) = –i á[,B] ñ. We easily obtain (, ) = 1. Then, using Eqs. (7) and (16) we obtain the final expression for the memory function

The calculation of the second moment, Eq. (20), can also be done directly and gives

which is, according to (1), the phonon frequency.

The Green function treatment for Hamiltonian (1) is standard [11-13] and, for this reason, we will present only the final result. The first non-vanishing correction, in a perturbation expansion, appears in the second order, and is given by

where the irreducible phonon self-energy 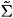(q,w) is defined by

with

The relationship between D(q,w) and the relaxation function is well known and is given by

where Im D(q,w) denotes the imaginary part of D(q,w). Using (24), we can write the relaxation function as

where

^' and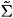 ^" represent, respectively, the real and imaginary parts of the phonon self-energy, .

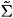Using the fact that the term (f_q , f_–q) w₂(q) in the numerator of Eq. (5) is equal to the unity, we see that Eqs. (5) and (25) have the same form if we replace wS in Eq. (5) by the function 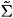appearing in (25). Comparing Eqs. (19) and (22), we see that wS would be identical to 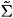if we had wA(q,k) = W_–A(q,k). Thus, there would be no difference between the two results obtained here if, in the numerator of (22), we could replace W_– by w. However, it can be seen that, in the summation to be done in Eq.(22), the main contribution comes from the region of w » W_–, and, then, the replacement w ® W_– can be considered as a good approximation.

At this point, it is relevant to make some comments about the Green function method and the interchange of W and w. Lets, then, consider the harmonic part of Hamiltonian (1)

because this Hamiltonian can be treated exactly. The (exact) relaxation function for the operator f_q defined in Eq. (2) is given by

However, if we apply the Green function technique to obtain the relaxation function for (26), we obtain

It is important to emphasize that both expressions, (27) and (28), are exact. In this case, the d-function allows us to interchange w and w₂(q). In Hamiltonians like (1), with other interaction terms, w₂(q) has to be replaced by W_– in the expression for the relaxation function. Due to the interaction terms, the peak linewidth becomes finite but is very narrow allowing us to interchange the two frequencies w ® W_– because the main contribution comes from the region around the peak.

We have thus shown that, for Hamiltonian (1), the memory function formalism, in the context of LTMM, at least to lowest order in the calculation, gives the same result as the Green function technique. The same conclusion holds true if we had considered a relaxation function involving the a_q operators.

Acknowledgements

This work was partially supported by CNPq ( Conselho Nacional de Desenvolvimento Científico e Tecnológico)

References

1. H. Mori, Prog. Theor. Phys. 34, 399 (1965).

2. R. Zwanzig, in Lectures in Theoretical Physics, edited by W.E. Brittin, B.W. Downs, and J. Downs (Interscience, New York, 1961), vol. 3, p.135.

3. A.S.T. Pires, Helvetica Phys. Acta 61, 988 (1988).

4. U. Balucani, M.H. Lee, and V. Tognetti, Physics Rep. 373, 409 (2003).

5. J.A. Plascak, A.S.T. Pires, and F.C. Sá Barreto, Solid State Commun. 44, 787 (1982). M.E. Gouvêa and A.S.T. Pires, Phys. Status Solidi(b) 146, 263 (1988); A.S.T. Pires and B.J.O. Franco, Solid State Commun. 54, 913 (1985).

6. S. Itoh, Y. Endoh, K. Kakurai, and H. Tanaka, Phys. Rev. Lett. 74, 2375 (1995); S. Itoh, H. Tanaka, and M.J. Bull, J. Phys. Soc. Jpn. 71, 1148 (2002).

7. C. Buragohain and S. Sachdev, Phys. Rev. B59, 9258 (1999).

8. M.H. Lee and R. Dekeyeser, Physica B 86-88, 1273 (1977).

9. S. Ayk, Phys. Rev. Lett. 56, 38 (1986).

10. G. Reiter and A. Sjölander, Phys. Rev. Lett. 39, 1047 (1977); T. Becher and G. Reiter, Phys. Rev. Lett. 63, 1004 (1989).

11. A.A. Abrikosov, L.P. Gorkov, and I.E. Dzyaloshinski, in Methods of Quantum Field Theory in Statistical Mechanics, (Prentice-Hall Inc, New Jersey, 1963).

12. M.J. Rice and S. Strassler, Solid State Commun. 13, 125 (1973).

13. M.C. Cross and D.S. Fisher, Phys. Rev. B19, 402 (1979).

14. J. Wagenhuber, K.W. Becker, and U. Rossler, Z. Phys. B73, 201 (1988).

15. J. Fivez, B. De Raedt, De Raedt, J. Phys. C: Solid State Phys. 14, 2923 (1981).

Received on 10 November, 2003; revised version received on 20 February, 2004

Publication Dates

• Publication in this collection
  04 Nov 2004
• Date of issue
  Sept 2004

History

• Reviewed
  20 Feb 2004
• Received
  10 Nov 2003