Dispersionless limit of integrable models

Dispersionless limit of integrable models

J. C. Brunelli

Universidade Federal de Santa Catarina

Departamento de Física - CFM

Campus Universitário - Trindade

C.P. 476, CEP 88040-900

Florianópolis, SC - Brazil

[e-mail]

Received 7 January, 2000

Nonlinear dispersionless equations arise as the dispersionless limit of well know integrable hierarchies of equations or by construction, such as the system of hydrodynamic type. Some of these equations are integrable in the Hamiltonian sense and appear in the study of topological minimal models. In the first part of the review, we will give a brief introduction to integrable models, mainly its Lax representation. Then, we will introduce the dispersionless limit and show some of our results concerning the two-component hyperbolic system of equations such as the polytropic gas and Born-Infeld equations.

I Introduction

The study of integrable models or solvable nonlinear partial differential equations is an active area of research since the discovery of the inverse scattering method [1-3]. These models are in a sense universal since they show up in many areas of physics such as solid state, nonlinear optics, hydrodynamics, field theory just to name a few. Also, integrable models are linked to many areas of mathematics (see the chart in http://www.ma.hw.ac.uk/solitons/procs/ bullough1/bullough1/bullough1.html) and have beautiful structures behind them.

In this review we want to approach the dispersionless limit of some integrable models and describe some of our work on this subject [4-7]. This review is organized as follows: In Section II we review or at least introduce some basic facts on integrable models. We use the Korteweg-de Vries equation (KdV) as an example. In Section III we introduce the dispersionless limit of an integrable model using the KdV equation to obtain the corresponding Riemann equation. Section IV reviews our work with a special class of dispersionless systems known as two-component hyperbolic systems. We show our results concerning the Hamiltonian structures for the Riemann equation [4] the dispersionless Lax representation for the polytropic gas dynamics [5] and Born-Infeld equation [6]. Finally, in Section V, we conclude with some problems that deserve further investigations.

II Integrable Models

II.1 Solitons

We are interested in nonlinear partial differential equations such as the sine-Gordon equation, nonlinear Schrödinger equation, Korteweg-de Vries equation (KdV), etc. These equations, as we will see, are very special since they are integrable. From now on we will illustrate the main results concerning integrability using the KdV equation.

The KdV equation has as solution what is called today a soliton. We can trace the discovery of the soliton back to 1834 with the Scott Russell's experiment [8] to generate solitary waves in water, i.e., localized single entity waves. A modern version of his experiment is shown in Fig. 1 (see http://www.ma.hw.ac.uk/~chris/scott_russel.html for an attempt to recreate Scott Russell's soliton). Scott Russell found that the volume V of water wave is equal to the volume of water displaced and that the speed c of the solitary wave is related with its amplitude a, depth of water h and acceleration of gravity g by

Figure 1.
Generation of a solitary wave.

This equation shows that higher waves travel faster. Attempts to obtain (1) theoretically were done by Boussinesq (1871) and Lord Rayleigh (1876) but an equation for u(x, t) in the small amplitude (h >> a) and in the long wave regime (h << l) was deduced by Korteweg-de Vries in 1895 [9]. This is the now famous KdV equation

where u(x, t) is the wave profile and u_t = , u_x = ,¼ .

The interest in the KdV equation (2) was resumed after studies of Fermi, Pasta and Ulam in 1955 [10] on numerical models of phonons in non-linear lattices, which are models closely related with the discretisation of the KdV equation. Motivated by these results, Zabusky and Kruskal in 1965 [11] studied numerically equations like (2) with periodic boundary conditions and were led to introduce the concept of soliton" solutions. In 1967 Gardner, Greene, Kruskal and Miura [12] solved equation (2) exactly, introducing the Inverse Scattering Transform Method" (ISTM), and were able to obtain its analytic expression. The so called 1-soliton and 2-soliton solutions of the KdV equation (2), for rapidly decreasing boundary conditions

are

In Fig. 2 we have pictures for the time evolution of the KdV solitons (3) (for some brief solitons movies see http://www.ma.hw.ac.uk/solitons and http://www.physics.otago.ac.nz/Physics100/simulations/ Gamelan/java/toda). The 1-soliton solution in Fig. 2 is the solitary wave obtained in the Scott Russell's experiment. Observe that as the time evolves the wave keeps its form. For the 2-soliton solution in Fig. 2, since the taller the soliton the faster it moves, the two solitons will interact nonlinearly when they meet. But, the amazing fact is that the two solitons will almost keep their initial form after interaction, there will be only a shift in their positions. This particle-like character and ability to retain its identity after interactions is what characterize a soliton solution of a nonlinear equation such as the KdV one.

Figure 2.
Time evolution for the solitons of the KdV equation.

II.2 Inverse Scattering

The next breakthrough in the soliton thread came in 1968 with the Lax [13] discovery about the meaning of the ISTM. His observation is that the KdV equation has the representation

where

are operators. Here ¶ º satisfies ¶f = f_x + f¶. We call L the Lax operator and in some sense we can find a Lax representation such as (4) for any integrable system. In this way, starting from (4), we can apply the ISTM for other nonlinear equations.

We can write the following eigenvalue problem for the Lax operator L

It is easy to see that since L evolves in time as (4) we have l_t = 0, i.e., the eigenvalue problem is isospectral. For the KdV equation (6) assumes the form

which is the time-independent Schrödinger equation and where t is a parameter (not the time in the Schrödinger equation). Now we can obtain a solution u(x, t) as follows: For some given initial condition u(x, 0) we solve (7) and obtain the scattering data S(t = 0), since u satisfies the KdV equation we can obtain the scattering data for any t, so from S(t) we use the inverse scattering (as we usually do in quantum mechanics) to find the potential" u(x, t) from the scattering data S(t). This is the ISTM routine and the main steps are illustrated in the diagram bellow.

II.3 Hamiltonian Systems

In 1970 Gardner [14] showed that the KdV equation is a Hamiltonian integrable system. Then, Faddeev and Zakharov in 1971 [15] were able to interpret the ISTM as a change of variables to the action angle variables. In fact, the representation of integrable models as integrable Hamiltonian systems is the starting point to the Quantum Inverse Scattering Method". Before we see how the KdV equation can be expressed in Hamiltonian form let us review the symplectic formalism for Hamiltonian systems. A Hamiltonian system is described by a phase space q_i, p_i, with i = 1, ..., N, and a Hamiltonian function H(p_i, q_i). The equations of motion are then given by the Hamilton's equations

Alternatively, we can describe a Hamiltonian system using Poisson brackets, for the dynamical variables A(q, p) and B(q, p), defined by

which is skew-symmetric and satisfies the Jacobi identity. The variables of phase space satisfy the canonical relations {q_i, q_j} = {p_i, p_j} = 0 and {q_i, p_j} = d_ij. The Hamilton's equations (8) assume the form

Putting the variables q_i and p_i in an 2N dimension column z the equations (8) assume the form

or

and even in a more compact form as

This is the symplectic formalism for Hamiltonian systems. The Poisson brackets can be written as

where J^ab = -J^ba and å(J^ab¶_dJ^bc + cyclic) = 0. The canonical relations are given by {z, z} = J and (10) by

We can perform some generalizations, allowing J to depend on z, J(z), and going from a discret sympletic space, of dimension 2N, to the continuum where we have now a field u(x, t) instead of z(t). Then, we have the following dictionary"

If there is a J^-1 we say that we are in a symplectic manifold, otherwise we are in a more general situation of a Poisson manifold. Note that the functional derivative is defined as

which for H[u] = u(x) yields

and for H[u] = òdx h(x, u, u_x, u_xx, ...)

where the right hand side is just the Euler-Lagrange operator acting on h.

Now, let us return to the KdV equation (2) and observe that it can be rewritten as

Introducing the Hamiltonian

we see that and = 0. The operator

is skew-adjoint and satisfies the Jacobi identity. So, (17) can be written in Hamiltonian form as

where

and we are omitting the explicit dependence on t.

Besides (18) the KdV equation (2) has an infinite number of conserved charges

and it can be shown that these charges are in involution, i.e.,

making the KdV equation integrable in Lioville's sense.

In 1978 Magri [16] discovered that equations like KdV have a second Hamiltonian structure. The operator

is skew-adjoint and satisfies Jacobi identity, and the KdV equation can be written in the alternative Hamiltonian form

where

These charges (22) are also in involution with respect to this second Hamiltonian structure

We say that the KdV equation is a bi-Hamiltonian system. In general we say that a system is bi-hamiltonian if there are Hamiltonian operators

₁ and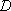 ₂ which are compatible, i.e., such that 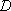₁, 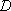₂ and l₁

₁ + l₂

₂ satisfy the Jacobi identity. It can be shown [16] that if a system is bi-Hamiltonian it is integrable in Lioville's sense.

Starting with the works of Gel'fand and Dickey in 1975 [17], Adler in 1979 [18] and many others, algebraic developments started to take place. The key role played by the Lax operator L, in obtaining the conserved charges H_n, the Hamiltonian structures, the hierarchy of equations that share H_n was then revealed. In the next sections we will introduce and apply some of these techniques in the dispersionless situation.

III Dispersionless Limit

We have seen that solitons preserve their shape and speed after collision. The soliton solution has a nondispersive nature. This is so not because dispersion effects are absent but because there is a compensation by the nonlinearities of the system. Let us look at the KdV equation (2) more closelly. If we eliminate the nonlinear term in (2) we get the linear dispersive equation

which admits the solution

This is a pure dispersive solution. In Fig. 3 we see that a initial configuration at t = 0 will disperse as time goes on. Eliminating the dispersive term we get the pure nonlinear equation

Figure 3.
The balance effects of dispersion and breaking in a soliton.

It can be easily checked by substitution that

with f arbitrary, satisfies (30). From this solution we conclude that the velocity of a point of the wave, with constant amplitude u, is proportional to its amplitude leading to the "breaking" of the wave, as shown in Fig. 3. The wave also develops discontinuities (indicated by the vertical dashed line in Fig. 3) in its evolution. The "miracle" of the soliton solution is due to a balance between the dispersion and the breaking of the wave, both phenonema placed together lead to the wave profile to propagate without changing its shape.

Equation (30) is called the dispersionless KdV or Riemann equation [19]. The interesting fact is that this equation is a integrable Hamiltonian system. We will return to study this equation in the next section but for the moment let us analyse how we get dispersionless equations. Dispersionless equations can be obtained by construction or as a quasi-classical limit of integrable ones [20] . In the latter case we make the scaling ® a , ® a and take the limit a ® 0. For the KdV equation (2) (we will change the constant factors on it, so instead of (5) we have L = ¶² + u and B = ¶³ + (¶u + u¶))

This is like the WKB aproximation in quantum mechanics and we will use it as our guideline [20].

Dispersionless integrable systems were introduced by Lebedev and Manin [21] and Zakharov [22], and although interesting on their own started to appear recently in developments in low-dimensional quantum field theory. It has been shown that there is a connection between 2-dimensional field theories and integrable equations of hydrodynamical type [23-25] (which are dispersionless systems). In 2-dimensional topological field theories [26] we are interested in calculating, from the partition function

the correlation functions

which depend only on the topology of the manifold M. The 2-point and 3-point correlation functions are given respectively by [27]

where t = (t¹, t², ..., tⁿ) are the coupling constants and F(t) is the free energy. The correlations (34) define a commutative and associative algebra (with an identity)

with e_a defining a basis for the algebra. The associativity of the algebra, (e_a°e_b)°e_g = e_a°(e_b°e_g), gives

These are the Witten-Dijkgraaf-Verlinde-Verlinde (WDVV) equations [26, 27] and can be identified with equations of hydrodynamic type. So, solutions of hydrodynamic equation can be identified with particular solutions of the topological field theory [25].

IV Two-Component Hyperbolic Systems

In a series of papers [28-31] Nutku and collaborators started to study dispersionless systems of equations that are in-between the simple Riemann equation [19] and the more general equations of hydrodynamic type [24]

In Fig. 4 we can find a chart with the main equations, of the two-component hyperbolic system type, studied on these papers.

A wealth of results concerning the integrability of these systems were revealled. Infinitely many conservation laws and multi-Hamiltonian structures were obtained. In this section we will be interested in reproduce some of these results from an algebraic point of view. In order to achive this goal we must understand the Lax representation for these systems.

IV.1 Riemann Equation

The Riemann equation

is the prototype for the hyperbolic systems. We address the following question: Is there a Lax representation for (37)? Yes, and we can obtain it performing the semiclassical limit [20] explained in Section 3. So, if the KdV equation goes to the Riemann equation (37) in the semiclassical limit, the Lax operator L = ¶²+u and B = ¶³ + (¶u + u¶) goes to the polynomials in the variable p

and the Lax representation (4) goes to

called dispersionless Lax representation (note the resemblance when we pass from quantum to classical mechanics doing ¶ ® p and [ , ]®{ , }). Here

is the dispersionless Poisson bracket [21, 22]. So, if we substitute (38) in (39) we get (37).

From now on we will apply some of the techniques described in [17] and [18] in a very informal way, since we want to give only a flavor of how the "machinery" works.

Let us calculate the square root of E in (38). So, we write the Laurent polynomial

and from E = E^1/2E^1/2 we obtain a₀, a₁, a₂, a₃, ..., or equivalently, we perform a series expansion for p ® ¥

Now we calculate E^3/2 = E^1/2E, E^5/2 = E^1/2E² and so on

The set of general Laurent polynomial A = gives rise to an associative algebra g = {A}. This algebra can be written as a direct sum g = g₊ Å g_-, where g₊ = {A₊} and g_- = {A_-} with A₊ = å_{i ³ 0}a_ipⁱ and A_- = å_{i < 0}a_ipⁱ, respectively. We can recognize M in (38) as

In fact, from (39) we are motivated to write

and we have a hierarchy of equations. We call it dispersionless KdV (or Riemann) hierarchy and we write

treating u as a function of k + 1 variables

For each t_k we have what is called a flow and it can be shown that they commute

consequently, the whole set of equations (45) is integrable since, as we have already pointed out, the Riemann equation is an integrable Hamiltonian system (all the equations in (45) share the same set of conserved charges).

The Riemann equation can be put in the form

It follows that the quantity H µ òdx u² is conserved. In fact òdx uⁿ are conserved as we can show explicitly. These conserved charges can also be obtained from E. Let be A any general Laurent polynomial

following [18] we introduce the Adler's trace as

which satisfies the usual relation TrAB = TrBA. From (42) and (43) we see that

and we have

with

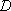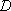_n = 0. From a Hamiltonian point of view the Riemann equation is a quadri-Hamiltonian system [30]. There are Hamiltonian operators ₁, ₂, 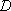₃ which are compatible and another Hamiltonian operator 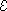which is compatible only with 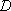₁. We can write

where

Hamiltonian structures can also be obtained from the Lax operator L (E in the dispersionless case). They are the symplectic structures of Kostant-Kirillov [32] on the orbits of the coadjoint representation of Lie groups [18, 33]. For dispersionless equations the corresponding Lie algebra is given by the associative algebra of Laurent polynomials endowed with the bracket (40). For the KdV equation the Lie algebra is given by the algebra of the pseudo-differential operators with the usual commutator. 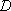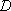Following this scheme the Hamiltonian structures ₁, ₂, 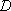₃ can be derived (see [4] for details) while we were not able to obtain 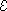from this scheme.

IV.2 Polytropic Gas Equation

We will try to apply the results of the last Section to some others dispersionless equations, such as the ones in the chart of Fig. 4. The polytropic gas dynamics equation

was studied from a Hamiltonian point of view in [30]. In (55) u is the velocity of the fluid, v is its density, f = v^g-2 and is related to the pressure (f(v) = ) and g is the ratio of specific heats (we call an ideal gas polytropic if the specific heats are constant over a large range of temperature).

The first step will be to derive a Lax representation for (55). We get a hint if we consider g = 2 in (55). In this case we have the shallow water equation [19] also known as the irrotational Benney equation [34]. Even though we do not know the dispersive system which originates (55) for any g we do know it for the case g = 2. This is the dispersive shallow water [35] equation, also called the two boson equation in field theory

This equation has the following nonstandard Lax representation [36, 37]

where (L²)_{³ 1} stands for the purely nonnegative (without p⁰ terms) part of the polynomial in p and J₀µ u, J₁µ v are the two bosons fields. Now, if we perform the semiclassical limit and do the appropriate identifications (56) yields (55) for g = 2 and from (57) we get the following dispersionless Lax representation

For any g we can use (58) as an ansatz to obtain the dispersionless Lax representation for (55) and it reads [5]

In [30] two sets of conserved charges were derived for (55) when g à 2. So, if (59) is really the correct Lax pair it must somehow provide both sets accordingly to the algebraic scheme described in the last section. In fact, since L has singularities in p = 0 and p = ¥ we can expand in powers of p in the two following ways

So, the first set of charges follows from

where the first densities are

and

which are the first set of charges obtained in [30]. The second set follows from

and the first densities are

where

is the second set of charges obtained in [30]

In (59) was expanded in p = ¥, a expansion around p = 0 provides a second consistent dispersionless Lax equation

which yields (with the proper rescaling) the equations

From the chart in Fig. 4 we recognize this equations as the polytropic elastic media equation.

IV.3 Born-Infeld Equation

With the Lax representation for the polytropic gas, obtained in the last section, we can get a Lax representation for the Born-Infeld equation given in the chart of Fig. 4

In (69) the Born-Infeld equation is expressed in the so called null coordinates version [31]. If we perform the transformation

we obtain the Born-Infeld equation written as a second-order equation in null coordinates

A Lax representation for (69) can be obtained as follows [6]. In the first place if we do the change of variables

called Verosky transformation [31], we will end up with the equation

known as the Chaplygin gas. In view of this it would be desirable to first obtain a Lax description of the Chaplygin gas like equations

This is indeed possible if we set g®-a, a ³ 1 in (59), so (74) can be obtained from

where is expanded around p = 0 and ()_{£ 1} is the polynomial in p that produces consistent equations, instead of the purely nonnegative polynomial used in (59). For a = 1 the Lax operator

reproduces (69). Again, conserved charges follows from

and the first Born-Infeld charges are

and these are exactly the charges derived in [31]. Another set is obtained from

and the first ones are

This is a new set of conserved charges, for the Born-Infeld equation (69), not found previously in [31].

Conclusions

We believe, from the results of the Section 4, that the study of dispersionless systems via a Lax representation is worthwhile. So, the search for a dispersionless Lax representation for the equations in the upper part of the chart in Fig. 4 is being pursued. Also, the derivation of the multi-Hamiltonian structures of these systems, as described in [28-31], is under investigation following the coadjoint orbit method [32, 33]. Another question that comes to mind is the dispersive generalization of these equations. Attempts in this direction can be found in [38].

Some topological equations are also related with the systems discussed here. For instance, the hyperbolic Monge-Ampère equation

may be related with the Born-Infeld equation as follows. If we perform the change of variables

the Monge-Ampère equation can be written as a first order system

and this equation can be related to the Chaplygin gas equation (73) through the following change of variables

Thus, we can give a Lax description for the hyperbolic Monge-Ampère equation through the Lax representation derived in Section 4.3. Finally, the Witten-Dijkgraaf-Verlinde-Verlinde (WDVV) equations (36), for n = 3, with

where t²º x and t³º t, yields the third order Monge-Ampère equation

This equation is a bi-Hamiltonian system and has a matrix Lax representation. It is then possible to generate a whole set of nonlocal charges much like the nonlinear sigma model (details are given in [7]). It is likely that a dispersionless sort of Lax representation for (86) may exist.

Acknowledgements

I would like to thank Ashok Das and Celso M. Doria for useful discussions. This work was supported by CNPq, Brazil.

References

[1] L. D. Faddeev and L. A. Takhtajan, Hamiltonian Methods in the Theory of Solitons, Springer-Verlag, 1987.

[2] A. Das, Integrable Models, World Scientific, 1989.

[3] P. G. Drazin and R.S. Johnson, Solitons: an Introduction, Cambridge University Press, 1989.

[4] J. C. Brunelli, Hamiltonian Structures for the Generalized Dispersionless KdV Hierarchy, Rev. Math. Phys. 8, 1041 (1996) (solv-int/961001).

[5] J. C. Brunelli and A. Das, A Lax Description for Polytropic Gas Dynamics, Phys. Lett. A235, 597 (1997) (solv-int/9706005).

[6] J. C. Brunelli and A. Das, A Lax Representation for the Born-Infeld Equation, Phys. Lett. B426, 57 (1998) (hep-th/9712081).

[7] J. C. Brunelli and A. Das, Non-local Charges and their Algebra in Topological Field Theory, Phys. Lett. B438, 99 (1998) (hep-th/9802070).

[8] J. Scott-Russell, Report on Waves, 14th Meeting of the British Association for the Advancement of Science, John Murray, London, 1844, p. 311.

[9] D. J. Korteweg and G. de Vries, On the Change of Form of Long Waves Advancing in a Rectangular Canal, and on a New Type of Long Stationary Waves, Philos. Mag. 39, 422 (1895).

[10] E. Fermi, J. Pasta and S. M. Ulam, Studies in Nonlinear Problems, Tech. Rep. LA-1940, Los Alamos Sci. Lab. (also in Collected Papers of Enrico Fermi, Vol. II, 1965, p. 978, Chicago University Press).

[11] N. J. Zabusky and M. D. Kruskal, Interaction of "Solitons" in a Collisionless Plasma and the Recurrence of Initial States, Phys. Rev. Lett. 15, 240 (1965).

[12] C. S. Gardner, J. M. Greene, M. D. Kruskal and R. M. Miura, Method for Solving the Korteweg-de Vries Equation, Phys. Rev. Lett. 19, 1095 (1967).

[13] P. D. Lax, Integrals of Nonlinear Equations of Evolution and Solitary Waves, Comm. Pure Appl. Math. 21, 467 (1968).

[14] C. S. Gardner, Korteweg-de Vries Equation and Generalizations. IV. The Korteweg-de Vries Equation as a Hamiltonian System, J. Math. Phys. 11, 1548 (1970).

[15] V. E. Zakharov and L. D. Faddeev, Korteweg-de Vries Equation: A Completely Integrable Hamiltonian Systems, Func. Anal. Appl. 5, 280 (1971).

[16] F. Magri, A Simple Model of the Integrable Hamiltonian Equation, J. Math. Phys. 19, 1156 (1978).

[17] I. M. Gel'fand and L. A. Dickey, Asymptotic Behaviour of the Resolvent of Sturm-Liouville Equations and the Algebra of the Korteweg-de Vries Equation, Russ. Math. Surveys 30, 77 (1975).

[18] M. Adler, On a Trace Functional for Formal Pseudodifferential Operators and the Symplectic Structure for the Korteweg-de Vries Type Equations, Invent. Math. 50, 403 (1979).

[19] G. B. Whitham, Linear and Nonlinear Waves, John Wiley & Sons, 1974.

[20] V. E. Zakharov, Benney Equations and Quasiclassical Approximation in the Method of the Inverse Problem, Funct. Anal. Appl. 14, 89 (1980).

[21] D. Lebedev and Yu. I. Manin, Conservation Laws and Lax Representation on Benney's Long Wave Equations, Phys. Lett. 74A, 154 (1979).

[22] V. E. Zakharov, On the Benney's Equations, Physica 3D, 193 (1981).

[23] I. Krichever, The Dispersionless Lax Equations and Topological Minimal Models, Comm. Math. Phys. 143, 415 (1992); The t-Function of the Universal Whitham Hierarchy, Matrix Models and Topological Field Theories, Commun. Pure Appl. Math. 47, 437 (1994); Whitham Theory for Integrable Systems and Topological Quantum Field Theories, in New Symmetry Principles in Quantum Field Theory, p. 309, ed. J. Fröhlich et al., Plenum Press, New York, 1992.

[24] B. A. Dubrovin and S. P. Novikov, Hydrodynamics of Weakly Deformed Soliton Lattices. Differential Geometry and Hamiltonian Theory, Russ. Math. Surv. 44, 35 (1989).

[25] B. Dubrovin, Integrable Systems in Topological Field Theory, Nucl. Phys. B379, 627 (1992); Geometry of 2D Topological Field Theories, preprint SISSA-89/94/FM, SISSA, Trieste, 1994, hep-th/9407018.

[26] E. Witten, On the Structure of the Topological Phase of Two-Dimensional Gravity, Nucl. Phys. B340, 281 (1990).

[27] R. Dijkgraaf, H. Verlinde and E. Verlinde, Topological Strings in d < 1, Nucl. Phys. B352, 59 (1991).

[28] Y. Nutku, On a New Class of Completely Integrable Nonlinear Wave Equations. I. Infinitely Many Conservation Laws, J. Math. Phys. 26, 1237 (1985).

[29] Y. Nutku, On a New Class of Completely Integrable Nonlinear Wave Equations. II. Multi-Hamiltonian Structure, J. Math. Phys. 28, 2579 (1987).

[30] P. J. Olver and Y. Nutku, Hamiltonian Structures for Systems of Hyperbolic Conservation Laws, J. Math. Phys. 29, 1610 (1988).

[31] M. Arik, F. Neyzi, Y. Nutku, P. Olver and J. M. Verosky, Multi-Hamiltonian Structure of the Born-Infeld Equation, J. Math. Phys. 30, 1338 (1989).

[32] A. A. Kirillov, Elements of the Theory of Representations, Springer Verlag, 1976; B. Kostant, Quantization and Unitary Representation, part I: Prequantization, Lect. Notes in Math. 170, 87 (1970); J. M. Souriau, Structure des Systems Dynamiques, Dunod, 1970.

[33] B. Kostant, Quantization and Representation Theory, London Math. Soc. Lect. Notes 34, 287 (1979); A. G. Reyman, M. A. Semenov-Tian-Shansky and I. B. Frenkel, Graded Lie Algebras and Completely Integrable Systems, Sov. Math. Dokl. 20, 811 (1979); A. G. Reyman and M. A. Semenov-Tian-Shansky, Reduction of Hamiltonian Systems, Affine Lie Algebras and Lax Equations. I and II, Invent. Math. 54, 81 (1979) and 63, 423 (1981); W. W. Symes, Systems of Toda Type, Inverse Spectral Problems and Representation Theory, Invent. Math. 59, 13 (1980); D. R. Lebedev and Yu. I. Manin, Gelfand-Dikii Hamiltonian Operator and Coadjoint Representation of Volterra Group, Funct. Anal. Appl. 13, 268 (1980).

[34] D. J. Benney, Some Properties of Long Nonlinear Waves, Stud. Appl. Math. 52, 45 (1973).

[35] L. J. F. Broer, Approximative Equations for Long Water Waves, Appl. Sci. Res. 31, 377 (1975); D. J. Kaup, A Higher-Order Water-Wave Equation and the Method for Solving It, Progr. Theor. Phys. 54, 396 (1975).

[36] B. A. Kupershmidt, Mathematics of Dispersive Water Waves, Commun. Math. Phys. 99, 51 (1985).

[37] J. C. Brunelli, A. Das and W.-J. Huang ,Gelfand-Dikii Brackets for Nonstandard Lax Equations, Mod. Phys. Lett. 9A, 2147 (1994).

[38] B. Enriquez, A. Yu Orlov and V. N. Rubtsov, Dispersionful Analogues of Benney's Equations and N-Wave Systems, Inverse Problems 12, 241 (1996).

Publication Dates

• Publication in this collection
  07 Jan 2002
• Date of issue
  June 2000

History

• Received
  07 Jan 2000