Noncommutative configuration space: classical and quantum mechanical aspects

Abstract

In this work we examine noncommutativity of position coordinates in classical symplectic mechanics and its quantisation. In coordinates {q i,p k} the canonical symplectic two-form is omega0 = dq i

Noncommutativity; Symplectic mechanics; Quantization

REGULAR ARTICLES

Noncommutative configuration space. Classical and quantum mechanical aspects

F. J. Vanhecke; C. Sigaud; A. R. da Silva

Instituto de Física, Instituto de Matemática, UFRJ, Rio de Janeiro, Brazil

ABSTRACT

In this work we examine noncommutativity of position coordinates in classical symplectic mechanics and its quantisation. In coordinates {qⁱ,p_k} the canonical symplectic two-form is w₀ = dqⁱÙdp_i. It is well known in symplectic mechanics [5, 6, 9] that the interaction of a charged particle with a magnetic field can be described in a Hamiltonian formalism without a choice of a potential. This is done by means of a modified symplectic two-form w = w₀-eF, where e is the charge and the (time-independent) magnetic field F is closed: dF = 0. With this symplectic structure, the canonical momentum variables acquire non-vanishing Poisson brackets: {p_k,p_l} = e F_kl(q). Similarly a closed two-form in p-space G may be introduced. Such a dual magnetic field G interacts with the particle's dual charge r. A new modified symplectic two-form w = w₀-eF+rG is then defined. Now, both p- and q-variables will cease to Poisson commute and upon quantisation they become noncommuting operators. In the particular case of a linear phase space R^2N, it makes sense to consider constant F and G fields. It is then possible to define, by a linear transformation, global Darboux coordinates: {xⁱ,p_k} = dⁱ_k. These can then be quantised in the usual way $widehat{\xi}^i,\widehat{\pi}^i $ = i(^h/_2p) dⁱ_k. The case of a quadratic potential is examined with some detail when N equals 2 and 3.

Keywords: Noncommutativity; Symplectic mechanics; Quantization

I. INTRODUCTION

The idea to consider non vanishing commutation relations between position operators [x,y] = i

², analogous to the canonical commutation relations between position and conjugate momentum [x,p_x] = i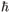, is ascribed to Heisenberg, who saw there a possibility to introduce a fundamental lenght 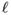which might control the short distance singularities of quantum field theory. However, noncommutativity of coordinates appeared first nonrelativistically in the work of Peierls [2] on the diamagnetism of conduction electrons. In the limit of a strong magnetic field in the z-direction, the gap between Landau levels becomes large and, to leading order, one obtains [x,y] = i

c/eB. In relativistic quantum mechanics, noncommutativity was first examined in 1947 by Snyder [3] and, in the last five years, inspired by string and brane-theory, many papers on field theory in noncommutative spaces appeared in the physics literature. The apparent unitarity problem related to time-space noncommutativity in field theory was studied and solved in [10]. Also (nonrelativistic) quantum mechanics on noncommutative twodimensional spaces has been examined more thorougly in the recent years: [11-16]. The above mentionned unitarity problem in quantum physics is also examined in Balachandran et al. [17].

In this work we discuss noncommutativity of configuration space in classical mechanics on the cotangent bundle T^*() and its canonical quantisation in the most simple case. In section we review the classical theory of a non relativistic particle interacting with a time-independent magnetic field F = 1/2 F_ij(q) dqⁱÙdq^j ; dF = 0. This is done in every textbook introducing a potential in a Lagrangian formalism. The Legendre transformation defines then the Hamiltonian and the canonical symplectic two-form dqⁱÙdp_i implements the corresponding Hamiltonian vector field. We also recall the less well known procedure of avoiding the introduction of a potential using a modified symplectic structure: w = dqⁱÙdp_i-eF. The coupling with the charge e is hidden in the symplectic structure and does not show up in the Hamiltonian: H₀(q,p) = d^kl p_k p_l/2m + (q). In section , a closed two-form in p-space, the dual field: G = 1/2 G^kl(p) dp_kÙdp_l, is added to the symplectic structure w = dqⁱÙdp_i-eF+rG, where r is a dual charge.

Such an approach with a modified symplectic structure has been previously considered by Duval and Horvathy [11, 14] emphasizing the N = 2-dimensional case in connection with the quantum Hall effect. We should also mention Plyushchay's interpretation [18] of such a dual charge r when N = 2 as the anyon spin. Considering here an arbitrary number of dimensions N, no such interpretation of r is assumed. The crucial point is that, now, both p- and q-variables cease to Poisson commute and upon quantisation they should become noncommuting operators. In the particular case of a linear phase space R^2N, it makes sense to consider constant F and G fields. It is then possible to define global Darboux coordinates with Poisson brackets {xⁱ,p_k} = dⁱ_k. These can then be quantised uniquely [1] in the usual way: [ⁱ,_k] = i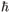dⁱ_k. However, in general, the dynamics become non-linear and there is no guarantee that the Hamiltonian vector field is complete. It is then not trivial to quantise the Hamiltonian, which becomes nonlocal. However, for a linear or quadratic Hamiltonian, this is possible and it is seen that the noncommutativity generates a magnetic moment type interaction. The cases N = 2 and N = 3 are discussed in detail in section . In section we examine the problem of symmetries in the modified symplectic manifold. Finally, in section general comments are made and further developments are suggested. In ^appendix we recall basic notions in symplectic geometry and in ^appendix we give a brief account of the Gotay-Nester-Hinds algorithm [7] for constrained Hamiltonian systems.

II. NON RELATIVISTIC PARTICLE INTERACTING WITH A TIME-INDEPENDENT MAGNETIC FIELD

A particle of mass m and charge e, with potential energy , moving in a Euclidean configuration space , with cartesian coordinates qⁱ, interacts with a (time-independent) magnetic field given by a closed two-form F(q) = F_ij(q) dqⁱÙdq^j. The dynamics is given by the Laplace equation:

Assuming to be Euclidean avoids topological subtleties, so that there exists a global potential one-form A(q) = A_i(q) dqⁱ such that F = dA. A global Lagrangian formalism can then be established with a Lagrangian function on the tangent bundle {t:T()®}:

The Euler-Lagrange equation is obtained as:

and coincides with the Laplace equation (II.1).

The Legendre transform

defines the Hamiltonian on the cotangent bundle {T^*() }:

With the canonical symplectic two-form

the Hamiltonian vector field of

_A is:

Its integral curves are solutions of:

which is again equivalent to (II.1).

If the second de Rham cohomology were not trivial, () ¹ 0, there is no global potential A and a local Lagrangian formalism is needed. This can be done enlarging the configuration space to the total space of a principal U(1) bundle over with a connection, given locally by A¹. This can be avoided using a global Hamiltonian formalism[20] in the cotangent bundle T^*() using a modified symplectic two-form:

and a "charge-free" Hamiltonian:

The Hamiltonian vector fields corresponding to an observable f(q,p) are now defined relative to w as w = df and given by:

With the Hamiltonian 0, the dynamics are again given by the Laplace equation (II.1) in the form:

The Poisson brackets, relative to the symplectic structure II.5, are:

In particular, the coordinates themselves have Poisson brackets:

Obviously, the meaning of the {q,p} variables in (II.3) and (II.5) are different. However both formalisms (w₀,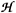A) and (w,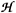0) lead to the same equations of motion and thus, they must be equivalent. Indeed, in each open set U homeomorphic to R⁶, the vanishing dF = 0 implies the existence of A such that F = dA in U and, locally:

Thus there exist local Darboux coordinates:

such that w = dxⁱÙdp_i, which is the form (II.3).

The dynamics defined by the Hamiltonian 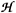0(q,p) = p²/2m+(q), with symplectic two-form w, is equivalent to the dynamics defined by the Hamiltonian 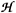A(x,p) = (p-e A(x))²/2m+(x) and canonical symplectic structure w = dxⁱÙdp_i. Equivalence is trivial since both symplectic two-forms are equal, but expressed in different coordinates {q,p} and {x,p}, related by (II.9). It seems worthwhile to note that a gauge transformation A®A' = A+gradf corresponds to a change of Darboux coordinates

{xⁱ,p_k} Þ {xⁱ' = xⁱ, = p_k+e¶_kf} ,

i.e. a symplectic transformation.

III. NONCOMMUTATIVE COORDINATES

Let us consider an affine configuration space = A^N so that points of phase space, identified with = R^2N = , may be given by linear coordinates (q,p). Together with the (usual) magnetic field F, we may introduce a (dual) magnetic field G = 1/2 G^kl(p) dp_kÙdp_l, a closed two-form, dG = 0, in space. Let e be the usual electric charge and r, a dual charge, which couples the particle with F and G. Consider the closed two-form:

In matrix notation this two-form (II.1) is represented as:

where[21] F = (1-eF rG) ; Y = (1-rG eF).

The fundamental Hamiltonian equation i_Xw = df, in (A.1), reads:

This can be rewritten as

Obviously, from (III.2) or (III.4), the closed two-form w will be non degenerate, and hence symplectic, if det(W) = det(Y) = det(F) ¹ 0, so that (W) has an inverse:

Explicitely:

The corresponding Poisson brackets are given by:

with the matrix

Explicitely:

In particular, for the coordinates (qⁱ,p_k), we have:

With 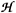(q,p) = (d^kl p_k p_l/2m)+(q), the equations of motion read:

The celebrated Darboux theorem guarantees the existence of local coordinates (xⁱ,p_k), such that w = dxⁱÙdp_i. When one of the charges (e,r) vanishes, such Darboux coordinates are easily obtained using the potential one-forms A = A_i(q)dqⁱ and Ã= Ã^k(p)dp_k, such that F = dA and G = dÃ.

Indeed, if r = 0, as in section II, Darboux coordinates are provided by xⁱ = qⁱ ; p_k = p_k+e A_k(q). A modified symplectic potential and two-form are defined by:

The Hamiltonian and corresponding equations of motion are:

which yields the second order equation in x, as in (II.1):

When e = 0, Darboux variables are

and we define

The Hamiltonian and equations of motion are now given by:

The second order equation, obeyed by p(!), is given by

Here the q-variable is assumed to be solved in terms of from equation _k = - ¶(q)/¶q^k and this is possible if det((q)) ¹ 0 !

In the case of nonzero charges (e,r) and non-constant F and G fields, there is no generic formula to define global Darboux coordinates (xⁱ,p_k). However, if the fields F and G are constant, the Poisson matrix (III.2) is brought in canonical Darboux form by a linear symplectic orthogonalization procedure, à la Hilbert-Schmidt. In the next section this is done explicitely for N = 2 and N = 3. Obviously such a linear transformation: (qⁱ,p_k)Þ(xⁱ,p_k) is defined up to a linear symplectic map of Sp(2n). These variables (xⁱ,p_k) Î R²ⁿ can be canonically quantised as operators obeying the commutation relations

As von Neumann taught us in [1], they are realised on the Hilbert space of square integrable functions of the variable x as

The original variables (qⁱ,p_k) being linear functions of the (xⁱ,p_k) are then also quantised.

When det(Y) = det(F) = 0, the closed two-form w is singular. When its rank is constant, w defines a presymplectic structure on phase space which we call the primary constraint manifold denoted by ₁. The consistency of the resulting constrained Hamiltonian system will be examined in the N = 2 and N = 3 cases.

IV. EXAMPLES: N = 2 AND 3

In the two examples below, we consider a classical Hamiltonian of the form

A complete resolution will be given for a harmonic oscillator potential:

Also of interest is the case of a constant ëlectric field": (q) = - E_k q^k, which is exactly solvable and left to the reader.

A. Dynamics in the noncommutative plane

The magnetic fields in two dimensions, are written as:

where B and C are pseudoscalars. The closed two-form (III.1) becomes

The equation i_Xw = df reads

Denoting c 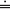(1+C B), the matrices F and Y are written as and Y^k_l = c d^k_l. The matrix (II.2) is then invertible if c does not vanish.

1. The non degenerate case

Here, we will assume c to be strictly positive. The above equation (IV.5) can then be inverted with Hamiltonian vector fields given by:

The Poisson brackets (III.11) become:

Substitution of the Ansatz

in the canonical Poison brackets, leads to the equations

We choose the solution:

such that (IV.8) reduces to (II.9) when C = 0 or to (III.17) in case B = 0. The 2-form (III.1) has the canonical Darboux form w = dxⁱÙdp_i in the variables

These have an inverse if, and only if c ¹ 0:

With the complex variables

the above changes of variables are written as:

The inverse transformations are:

The Hamiltonian (IV.2) becomes

where L is angular momentum

The "renormalised" mass and elasticity constant are given by:

where

The corresponding frequency is given in terms of the "bare" frequency w₀ = by:

and , the induced Larmor frequency, by:

The solution of Hamiltonian's equations with (IV.16) is standard. With[22]

reduced variables are introduced by:

The original (q,p) are expressed as:

where

The symplectic structure and the Poisson brackets are:

The fundamental nonzero Poisson bracket is

In these variables, the Hamiltonian (IV.16) reads:

where

The corresponding equations of motion are:

With the shift variables

the symplectic structure and the Poisson brackets are given by:

with fundamental nonzero brackets:

The Hamiltonian, with the (positive !) frequencies

reads now:

The corresponding equations of motion and their solutions are given by:

The relations between variables are given by:

The inverse transformations are:

Quantisation is trivial though the substitution of the fundamental Poison brackets (IV.27),(IV.34) by operator commutators

Having kept the initial ordering, the quantum Hamiltonian has eigenvalues:

where n_(±) are nonnegative integers. The corresponding eigenvectors are denoted by |n₍₊₎,n_(-) > .

2. The degenerate or constraint case

The condition c 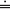(1+BC) = 0 determines w as a presymplectic structure on and shall be called the primary constraint. Again, the notation is simplified using complex variables[23]. The presymplectic two-form reads

The Hamiltonian (IV.2) becomes

Writing a vector field as

The homogeneous equation, i_Zw = 0 has nontrivial solutions. Indeed, with U₀ = Z¹+iZ² and V₀ = Z₁+iZ₂, equation (IV.45) yields the system:

of which the determinant is c = 1+BC = 0.

The inhomogeneous equation i_Xw = d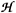, i.e. the Hamiltonian dynamics, reads

It will have a solution if

This condition, termed secondary constraint, is explicitely given by:

For the Hamiltonian (IV.44) this condition (IV.49) is linear:

and defines the secondary constraint manifold 2.

, a particular solution of i_Xw = d is given by:

The general solution is given by:

where (U₀,V₀) is restricted to obey (IV.46). This vector field, restricted to 2, should conserve the constraints i.e. must be tangent to 2:

The vector fields U and V are completely defined on 2, with ensuing equations of motion:

In terms of the frequency:

the solution is given by

Obviously, if q₀ and p₀ obey the secondary constraints (IV.50), q(t) and p(t) obey them at all times.

The same result can be obtained by symplectic reduction, restricting the pre-symplectic two-form (IV.43) to 2:

The fundamental Poisson bracket is

The dynamics are given by:

And, with the reduced Hamiltonian

_r given by

this yields equation (IV.56). When B > 0, hence C < 0, we define

such that

Quantisation is again trivial introducing operators a and a^†;, obeying

such that the quantum Hamiltonian

has eigenvalues:

3. The c ® 0 limit of (IV A 1).

We need the expansion of

in powers of e = , where 1+bc = e² and 2u = 1+e.

Also, from (IV.25), we obtain

For definitenees, we assume in the following B > 0 and so C < 0 in the limit e ® 0. We obtain

Also:

One of the frequencies w₍₊₎ diverges, while the other w_(-) tends to w_r defined in (IV.55). The relations in (IV.39) yield the initial conditions:

The solutions (IV.40), in the e ® 0 limit are then written as

The first term is a fast oscillating function with diverging frequency and so averages to zero. Furthermore, if the initial conditions are on

₂, i.e. if (q₀+i|B|p₀/(mw₀)²) = 0, this first term behaves as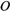 (e) exp{int/e²} converging to zero. The second term is then reduced to the expression (IV.56) of q(t). Similar considerations hold for p(t) in such a way that the solution stays on M₂.

B. Noncommutative R³

In R³, the magnetic fields F and G are written in terms of pseudovectors = {B^k} and C = {C_k} as:

The closed two-form (III.1) is written as:

The fundamental equation i_Xw = df f reads

Defining J = C· = C_k B^k and c = 1+J, this is also written as

The 3×3 matrices F and Y read:

F_i^j = c d_i^j-C_i B^j ; Y^k_l = c d^k_l-B^k C_l ,

with detF = detY = c². Assuming again c¹ 0[24], these matrices have inverses:

The Hamiltonian vector fields are obtained from (IV.78):

The Poissson brackets are given by:

The Ansatz (IV.8) has to be generalised to

For a,b similar equations as in (IV.9) are obtained:

with a the same solution (c assumed to be strictly positive):

Furthermore, there is an additional equation for a':

Substituting (IV.83), one obtains

with solution, remaining finite when J ® 0,:

The formulae (IV.81) are finally written as:

In old fashioned vector notation, this appears as:

The inverse formulae of (IV.86) are obtained as:

Or, in vector notation:

where

Again, for sake of simplicity, we consider a configuration space which is Euclidean = E³ with metric <;> = d_ij vⁱ w^j = (v·) such that v_i= d_ij vⁱ. Substitution of (IV.88) in a Hamiltonian of the form (IV.2), leads to a Hamiltonian quadratic in (x,p) and to a system of linear evolution equations. In the case when and C point in the same direction:

a particularly simple Hamiltonian is obtained. Parallel coordinates are defined by x³ , p₃ and transverse coordinate vectors by ^ = - x³

_Z and p_^ = p - p₃e_Z. Indeed, eq. (IV.88) becomes

The Hamiltonian is:

The transverse degrees of freedom are seen to have a renormalised[25] mass and elasticity constant which are given by the same expressions as in (IV.18):

where

The fields and C induce a sort of magnetic moment interaction along the Z-axis with the same Larmor frequency as before:

where L₃ = x¹p₂-x²p₁. Acrtually, the condition (IV.91) reduces the (N = 3) case to a sum (N = 2)Å(N = 1). The three relevant frequencies of our oscilator are:

The spectrum of the quantum Hamiltonian is easily obtained as

where n_(±),n₃ are nonnegative integers. Corresponding eigenvectors are denoted by |n₍₊₎,n_(-),n₃ > .

V. SYMMETRIES

For Euclidean configuration space º E^N, with metric d_ij, an infinitesimal rotation is written as:

where (M_ab)ⁱ_j= dⁱ_a d_bj-dⁱ_b d_aj are the generators of the rotation group obeying the Lie algebra relations:

This induces the push forward in T^*():

In a basis[26] {e_ab} of (SO(N)), let u = (1/2)e_abu^ab denote a generic element. With (u) = exp{u^ab M_ab}, finite rotations are written as

The vector field X_u (see ^{appendix A}) is given by its components:

It conserves the canonical symplectic potential and two-form:

_Xuq₀ = 0 ; _Xuw₀ = 0 .

The action is in fact Hamiltonian for the canonical symplectic structure. With the notation of ^{appendix A}, we have

In terms of the momenta , the rotation (V.98) reads

The Lie algebra relations (V.99) become Poisson brackets:

Naturally, for the modified symplectic structure (III.1), the action (V100) will be symplectic if, and only if, the magnetic fields obey:

For constant magnetic fields, this holds if (u) belongs to the intersection of the isotropy groups of F and G, which, in three dimensions, is not empty if both magnetic fields are along the same axis. A rotation along this "z-axis" is then symplectic. However, in general it will not be Hamiltonian and there will be no momentum _Z such that dq = {q,_Z}. Again the discussion simplifies when one of the charges r or e vanishes. If the potentials A or à are invariant under (u), then the action is Hamiltonian[27] with momentum defined by the symplectic potentials (III.13) or (III.18) as

Obviously there is always an SO(N) group action on the (x,p) coordinates which is Hamiltonian with respect to (III.1) and momentum given by:

However, the hamiltonian (IV.2), looking apparently SO(N) symmetric, is explicitely seen not to be so when expressed in the (x,p) variables.

VI. FINAL COMMENTS

The symplectic structure in cotangent space, T^*() , was modified through the introduction of a closed two-form F on T^*, which has the geometic meaning of the pull-back of the magnetic field F, a closed two-form on : F = k^*(F). A first caveat warns us that the other closed two-form G does not have such an intrinsic interpretation. Indeed, it is obvious that a mere change of coordinates in will spoil the form (III.1) of w. This means that our approach must be restricted to configuration spaces with additional properties, which have to be conserved by coordinate changes. The most simple example is a flat linear[28] space = E^N, when () is assumed to hold in linear coordinates. Obviously, a linear change in coordinates will then conserve this particular form. Although the restriction to constant fields F and G is a severe limitation[29] it allowed us to find explicit Darboux coordinates (IV.8) when N = 2 and (IV.81) when N = 3.

Finally, when det{\Een- rG eF} = 0, the closed two-form w is degenerate with constant rank and defines a pre-symplectic structure on T^*(). Its null-foliation decomposes T^*() in disjoint leaves and on the space of leaves, w projects to a unique symplectic two-form. In two dimensions, the representations of the corresponding quantum algebra in Hilbert space and its reduction in the degeneracy case were studied in [11-14,18].

References

[1] J. von Neumann, Math. Annalen 104, 570 (1931).

[2] R. Peierls, Z. Phys. 80,763 (1933).

[3] H. S. Snyder, Phys. Rev. 71, 38 (1947).

[4] A. Messiah, Mécanique Quantique I, Dunod,1962.

[5] J-M. Souriau, Structure des systèmes dynamiques, Dunod, 1970.

[6] R. Abraham and J. E. Marsden, Foundations of Mechanics, Benjamin, 1978

[7] M. J. Gotay, J. M. Nester, and G. Hinds, J. Math. Phys. 19, 2388 (1978).

[8] A.P. Balachandran, G. Marmo, B-S. Skagerstam, and A. Stern, Gauge Symmetries and Fibre Bundles, Lect. Notes in Physics 188 (1983).

[9] V. Guillemin and S. Sternberg, Symplectic Tecniques in Physics, Cambridge University Press, 1984.

[10] S. Doplicher, K. Fredenhagen, and J. Roberts, Comm. Math. Phys. 172, 187 (1995).

[11] C. Duval and P. A. Horvàthy, Phys. Lett. B 479,284 (2000).

[12] V. P. Nair and A. Polychronakos, Phys. Lett. B 505, 267 (2001).

[13] B. Morariu, and A. Polychronakos, Nucl. Phys. B 610, 531( 2001) and Nucl. Phys. B 634, 326 (2002).

[14] P. A. Horvàthy, Ann. Phys. 299, 128 (2002).

[15] A. E. F. Djemaï and H. Smail, arXiv:hep-th/0309006(2003).

[16] A. Bérard and H. Mohrbach, arXiv:hep-th/0310167(2003) and arXiv:hep-th/0404165(2004)

[17] A. P. Balachandran, T. R. Govindarajan, C. Molina, and P. Teotonio-Sobrinho, arXiv:hep-th/0406125, (2004).

[18] P. A. Horvàthy and M. S. Plyushchay, Phys. Lett. B 595, 547 (2004).

[19] See e.g. [8]

[20] Well known in symplectic mechanics, see e.g.[5, 6, 9].

[21] Observe that Fk' = dk ' ¡ eFk j rGj' and Yⁱ_j = dⁱ_j - rGi' eF' j are mutually transposed and that the matrices Yk j rGj' = rGk jFj ' and Fk j eFj' = eFk jYj ' are antisymmetric.

[22] In the limit c ® 0, we have m'w'₀=$\sqrt{m^\prime, \kappa^\prime}$® |B|.

[23] Recall that with complex variables q = q1 + iq2, the diferentials dq = dq1 +idq2 and dq^†; = dq1 - idq2 have local dual vector fields {¶=¶q = (¶=¶q¹ - i¶=¶q²)/2 ; ¶=¶q^†; = (¶=¶q¹ + i¶=¶q²)/2 and similarly for the p = p1 + ip2 variables.

[24] The (N = 3) case wil only be examined in the nondegenerate case c > 0.

[25] Due to k²+k'²(rC)² (eB)²+2kk' rCeB=1, the mass and elastic constant of the z degrees of freedom, as expected, are not renormalised.

[26] with dual basis {e^ab} in L*(SO(N)).

[27] Exercise 4.2A in [6], defining a (generalized) Poincar´e momentum.

[28] Quantum mechanics on a noncommutative shere S² and on general noncommutative Riemann surfaces was examined in ([12, 13].

[29] In the case e = 0, Darboux coordinates are given by (III.17) and in [16] such model was considered with the possibility of having a monopole in p-space!

[30] T_f (t)* denotes the pull-back of T_f (t) and L is the Lie derivative along X_f .

[31] We use L_X = di_X +i_X d on differential forms.

[32] M₁ is the primary constrained manifold, arising e.g. from a degenerate Lagrangian.

Received on 17 October, 2005

To each observable, which is a differentiable function f on {,w}, the symplectic structure associates a Hamiltonian vector field:

Such a vector field generates a one-parameter (local) transformation group:

_f(t):® :z₀® z(t), solution of dz(t)/dt = X_f(z(t)) , z(0) = z₀.

In particular, the Hamiltonian 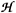generates the dynamics of the associated mechanical system. With the usual interpretation of time, is assumed to be complete such that its flux is defined for all t Î [-¥,+¥]. Transformations, induced by an Hamiltonian vector field X_f, conserve the symplectic structure[30]:

More generally, the transformations conserving the symplectic structure form the group Sympl() of symplectomorphisms or canonical transformations. Vector fields obeying 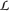_Xw = 0, generate canonical transformations and are called locally Hamiltonian, since [31] di_Xw = 0 implies that, locally in some U Ì , there exists a function f such that df_|U = (i_Xw)_|U.

The Darboux theorem guarantees the existence of local charts U Ì with coordinates {qⁱ,p_k} such that, in each U, w is written as:

In the natural basis {¶/¶qⁱ,¶/¶p_k} of T_z(), the Hamiltonian vector fields corresponding to f reads

The Poisson bracket of two observables is defined by: {f,g} 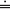w(X_f,X_g), with the following properties:

{f1,f2}=-{f2,f1}

{f1,g1 g2}={f,g1} g2+g1{f,g2}

{f,{g1,g2}}={{f,g1},g2}+ {g1,{f,g2}}

These properties, relating the pointwise product g₁·g₂ with the bracket {f,g}, are said to endow the set of differentiable functions on with the structure of a Poisson algebra (). In a coordinate system (z^A), where w = w_AB dz^AÙdz^B, it is given by:

where L is minus w^-1. In Darboux coordinates it reads:

The Poisson brackets of the Darboux coordinates themselves are:

The dynamical evolution of an observable is given by:

A Lie group G acts as a symmety group on a symplectic manifold , if there is a group homomorphism :G ® Sympl():g ® (g). An infinitesimal action defined by a Lie algebra element u Î is given by the locally Hamiltonian vector field

When each X_u is Hamiltonian, the group action is said to be almost Hamiltonian and {,w} is called a symplectic G-space. In such a case, a linear map : ® ():u ® (u) can always be constructed such that X_u = w^#(d (u)). When there is a which is also a Lie algebra homomorphism: ([u,v]) = {(u),(v)}, the group is said to have a Hamiltonian action and {,w,} is called a Hamiltonian G-space. Since is linear in , it defines a momentum mapping from to the dual ^* of the Lie algebra defined by: á(z)|uñ = (u,z). When is a Hamiltonian G-space, the momentum mapping is equivariant under the action of G on and its co-adjoint action on ^*.

In general there may be topological obstructions to such a Lie algebra homomorphism. However, when G acts on : j:G ® Diff():g ® j(g):q ® q^' = j(g)q, the action is extended to a symplectic action in { = T^*(),w₀}: :G ® Sympl():g ® (g): (q,p) ® (q',p'), where p' is defined by p = (j(g))p'. It follows that (g)^*q₀ = q₀ ; (g)^*w₀ = w₀. The infinitesimal action is given by X_u(z) = (d(exp(tu))z/dt)_{|t = 0} and q₀ = 0 ; w₀ = 0. From (X_u) = dáq₀|X_uñ, it follows that the action is almost Hamiltonian with (u) = áq₀|X_uñ. Moreover, since áq₀|X_[u,v]ñ = w₀(X_u,X_v) = {(u),(v)}, the action is Hamiltonian and {T^*(),w₀,} is a Hamiltonian G-space.

APPENDIX B: PRESYMPLECTIC MECHANICS

A manifold

₁, endowed with a closed but degenerate[32] 2-form w, with constant rank, is said to be presymplectic. The mapping w^b has a nonvanishing kernel, given by those nonzero vector fields X₀ obeying w^b(X₀)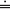 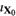w = 0. The fundamental dynamical equation

has then a solution if

If this is nowhere satisfied on

₁, the hamiltonian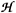 does not define any dynamics on ₁. When (B.2) is identically satisfied, a particular solution X_P of (B.1) is defined in the entire manifold ₁ and so is the general solution obtained summing the general solution of the homogeneous equation 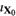w = 0, i.e X_G = X_P+X₀, which will contain arbitrary functions. When (B.2) is satisfied for some points z Î ₁, we shall asssume they form a submanifold, called the secondary constrained submanifold with injection i₂:₂

₁. The particular solution X_P of (B.1) is now defined in ₂ and so is the general solution X_G. Requiring that X_G conserves the constraints amounts to ask that X_G is tangent to ₂:

Again, when there are no points where this tangency condition is satisfied, (B.1) is meaningless. Another possibility is that some of the arbitrary functions in X₀ become determined and the tangency condition is obeyed on the entire ₂. The general solution then still contains some arbitrary functions. Finally it may happen that the conditions (B.3) are only satisfied on some ₃ with i₃: ₃

₂. The story then goes on until one of the first two alternatives are reached.

appendix

,w} be a symplectic manifold with symplectic structure defined by a two-form w which is closed, ) ® ): ) ® ):a ® w) of a differential configuration space . In a coordinate system {, a cotangent vector may be written as aº ) and an associated holonomic basis {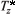(). The canonical one-form is defined as q -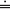

Let {,w} be a symplectic manifold with symplectic structure defined by a two-form w which is closed, dw = 0, and nondegenerate such that the induced mapping w^b:T() ® T^*(): X ® i_Xw has an inverse w^#:T^*() ® T():a ® w^#(a). The paradigm of a (non-compact) symplectic manifold is a cotangent bundle T^*() of a differential configuration space . In a coordinate system {qⁱ} of , a cotangent vector may be written as a_q = p_i dqⁱ. This defines coordinates z Þ {qⁱ,p_k} of points z Î º T^*() and an associated holonomic basis {dp_k, dqⁱ} of 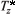(). The canonical one-form is defined as q₀

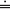p_i dqⁱ. Obviously, the exact two-form w₀ - dq₀ = dqⁱÙdp_i is symplectic.

Publication Dates

• Publication in this collection
  10 Apr 2006
• Date of issue
  Mar 2006

History

• Received
  17 Oct 2005