Bidimensional instability in antiferroelectric liquid crystals

Bidimensional Instability in Antiferroelectric Liquid Crystals

M. Becchi^1,2, S. Ponti^1,2, A. Strigazzi^1,2, V. Chigrinov^3,4, and S. Torgova^2,5

¹ Dipartimento di Fisica and I.N.F.M., Politecnico di Torino,

Corso Duca degli Abruzzi 24, I-10129 Torino, Italy

² Joint Laboratory of Orientationally Ordered Media (OOM-Lab),

C. Duca degli Abruzzi 24, I-10129 Torino, Italy

³ Institute of Crystallography, Leninski pr. 52, Moscow, Russia

⁴ Hong Kong University of Science and Technology, China

⁵ SSC RF "NIOPIK"(Organic Intermediates & Dyes Institute),

B. Sadovaya 1/4, Moscow 103787, Russia

Received on 30 January, 2002

In the last decade it has been experimentally found a periodic domain pattern arising in smectic C^* liquid crystals in surface stabilized bookshelf geometry. Such a periodic texture appears after switching-off an external electric field, even in strong anchoring conditions. It has a static character and can be bidimensional, being dependent on both directions normal to the smectic planes and normal to the cell plates. In the present work an explanation to this phenomenon is proposed. According to our model in the antiferroelectric phase the biperiodic texture is a threshold phenomenon, appearing for values of the spontaneous polarization greater than a critical value, whereas in the ferroelectric phase this type of bidimensional instability is hindered.

I Introduction

The importance of Ferroelectric Liquid Crystals (FLC) is strictly related to the nonlinear electro-optic effect determined by the coupling of the spontaneous polarization with an external applied electric field [1]. The effect can be characterized by bistability and optical memory in the surface stabilized bookshelf [2, 3] or quasi bookshelf [4] configuration. In this case, each single layer exhibits a uniform spontaneous polarization, oriented in the same way in the whole cell (see Fig.1 a).

But some smectic C^* materials, like MHPOBC, due to their molecular structure [5] can present also a dual arrangement, in which consecutive layers naturally have alternative sense of - antiferroelectric phase (AFLC). In this state the whole cell spontaneous polarization vanishes. An AFLC under applied electric field can move towards other two stable states, up- and down- via an azimuthal rotation df = ±p of alternate layers (see Fig.1 b), allowing to obtain a tristability behaviour [3]. In the last decade, the appearance of static modulated pattern was observed, both in ferroelectric- and in antiferroelectric phase [6]-[12], for instance after switching off a DC field applied to a uniform surface stabilized cell. Regular periodic domains occur in this case as static stripes, oriented either parallel [8-11] or perpendicular [6, 7, 12] to the smectic layers normal, which lies in a plane parallel to the cell walls (see Fig. 2).

Up to now several qualitative models describe the possible role played by the presence of a periodic disclination array [13], by flexoelectricity and charge conduction [12].

The purpose of the present paper is to investigate a new mechanism, explaining the biperiodic instability as the result of a competition between the polarization-field coupling and the coulombian interaction between the polarization charges in the smectic layers. This competition is driven by the anchoring, mediated by the bulk elasticity [14], biased by the dielectric contribution and corrected by the flexoelectricity [15].

II Theory

Let us consider a bookshelf arrangement of a material exhibiting both ferroelectric - and antiferroelectric- phases, like MHOPBC. The cell reference frame [x, y, z] has x-axis normal to the cell walls, y-axis parallel to the the glass plates and to the smectic planes, z-axis normal to the smectic planes (see Fig. 1a). 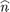is the molecular director, and 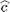is the tilt director. q is the polar angle characterizing the tilt cone, whereas f is the azimuth of the 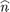-director orientation (see Fig. 1b). Any variation dq is connected with a hard distortion, hindered at constant temperature; instead, any variation df is allowed, describing a soft distortion. The LC spontaneous polarization =P_s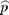, where 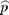= 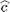× 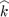( 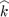is parallel to the z-axis), lies in the smectic layer parallel to xy-plane. The initial configuration of 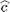is parallel to y-axis (f₀ = p/2). By applying an external electric field along z the linear coupling with the polarization produces a certain azimuthal rotation (f-f₀). After switching off the field, the 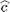-distribution relaxes to a configuration different with respect to the previous one. The new configuration is biperiodically distributed in zx-plane, being invariant along y-axis. To describe the modulated pattern, it is convenient to define

where the wave amplitude |j|

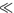
f

₀. Moreover, the tilt-director

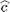
is given by

The free energy density of the whole cell accounts for the following contributions:

Elastic term

The elastic energy involved in a distortion, where any curvature of smectic plane is prohibited, is given by [16]:

where j

_xº ¶j/¶

x,j

_zº ¶j/¶

z and

B

_i and

B

₁₃ are smectic elastic constants. More precisely,

B

₁ describes the bend of smectic director

,

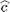
B

₂ the splay of smectic director

,

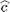
B

₃ the twist of smectic director

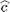
, and

B

₁₃ is a mixed bend-twist of the nematic director

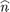
, which vanishes in one-constant approximation [3].

Flexoelectric term

The flexoelectric polarization is defined as [15]:

where

d

_i are flexoelectric moduli.

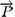
_f(

x,

z) writes

turning out to be bidimensionally modulated as well, then creating an internal field

(

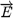
x,

z), characterized by the potential Y(

x,

z):

being |Y(

x,

z)|

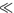
P

_s

D

_x, where

D

_x is the cell thickness. In the local frame [

,

,

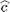
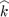
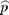
] the internal field

(

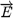
x,

z) is:

and couples with

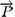
_f, giving

Dielectric term

The dielectric contribution to the cell free energy density writes

where

The rank 2 dielectric tensor

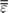
(e

_||, e

_p, e

_t) has only its diagonal components different from zero [16, 17], expressed in the intrinsic frame [

,

,

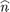
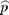
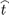
] where

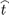
is the transverse unit vector

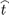
º

×

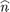
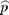
. It takes into account the bonded charges separation in the chiral liquid crystal. Due to the fact that the wave amplitude |j| of the periodic distortion is much smaller than f

₀, the director

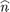
reads

Thus, from Eqs. (9 - 11) the free energy term is

and eventually becomes

Electrostatic interaction term among bonded charges

The Coulomb interaction free energy density between spontaneous polarization charges Q, Q¢ separated at the same surface in correspondence of two smectic layers l, l¢ is given by

where

V is the relevant volume,

,

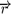
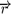
¢ are the positions of

Q,

Q¢, and the sign to be chosen is either (+) or (-) respectively for ferroelectric- and antiferroelectric -phases, according to the fact that interacting dipole charges separated at the same cell surface are of the same or different signs. This means that a chiral LC in ferroelectric state has a repulsive coulombian potential, since the charges separated at the same surface in correspondence of adjacent layers have the same sign (

f

_C = a

²

Q

²/

d ), whereas in antiferroelectric state it has attractive coulombian potential, since the charges separated have alternatively opposite sign (

f

_C = -a

²

Q

²/

d ) - note that a is a convenient constant and

d is the smectic layer thickness. More precisely

f

_C writes

where s, s¢ are the surface charges densities at the walls,

dA,

dA¢ are the relevant surface elements and

D

_i is the cell size along the

i-direction. Putting

P

_s,

as the involved spontaneous polarizations, the corresponding charges are

Approximating Dirac delta function by d(

z) = 1/|

z-

z¢|, the integration of Eq. (15) over the whole cell gives

The local spontaneous polarization is

and the divergence is

The Coulomb term eventually reads

where (+) and (-) are relevant to the ferroelectric- and antiferroelectric- states, respectively. The total bulk free energy density is the sum of all contributions already mentioned:

In the hypothesis that the anchoring is strong, the total free energy coincides with the total bulk free energy. By minimizing it with the usual procedure, the Euler-Lagrange Eqs.

can be written as

where d º (d₃ + d₆)/2, d^*º d₄ - d₉ are combinations of the flexoelectric moduli. System (23) is comprising two 2^nd order linear differential equations in the azimuth j(x,z) and the internal electric potential Y(x, z). The system admits harmonic solutions as the following:

where

q

_x,

q

_z represent the wave-vector of the possible biperiodic coupled distortion. By substituting Eq. (24) into linearized Euler- Lagrange Eqs. (23), a linear system in j(

x,

z), Y(

x,

z) is obtained. The nontriviality condition yields to the dispersion relation

where the wave-vector ratio is defined as

The minimum value of

r, which satisfies the condition (25), determines the threshold of the appearance of the biperiodic instability. In the case of strong anchoring, it turns out to be

since at the cell walls the director is kept in its undeformed position: j(

x = 0,

z) = 0, j(

x =

D

_x,

z) = 0, and the minimum energy distortion has the wavelength l

_x equal to the double cell thickness, l

_x=2

D

_x, where

D

_x» 2 mm.

If the elastic constants for bend B₁ and for splay B₂ are equal and if the dielectric permittivity is isotropic, e_|| = e_p = e_tº e, the dispersion relation can be written more simply as

resulting in a 4^th degree algebraic equation. Let us remind the correspondence between the smectic C^* and the nematic elastic constants

where the smectic tilt q = q(

T) is only dependent on temperature

T. At room temperature

T = 25

^°

C it has the typical value q ~ 20

^°. The usual values of the other relevant parameters are

B

₁ ~

B

₂ ~

B

₃ ~ 0.1 ¸0.5,

K

_ii ~ 10

^-6dyn,

B

₁₃ ~ ±

B

₁ ~ ±10

^-6dyn,

d ~ 10

^-5dyn,

d

^* ~ ±10

^-5dyn,

P

_s ~ (0.05¸50)nC/cm

², f

₀ ~ 10

^°¸90

^°, e = 1 . Hence the last term of Eq. (28) turns out to be negligible. If the elastic coupling no commar bend-twist,

B

₁₃ is negligible (for rigid smectic planes,

B

₁₃=0) and if the splay does not influence the phenomenon (

B

₂=0), thus (28) reduces to

giving simply:

We point out that only in antiferroelectric state this model predicts the existence of the biperiodic distortion for smectic C^* cells in bookshelf geometry with strong anchoring. Then in the case of elastic- and dielectric- isotropy, by neglecting the flexoelectrical corrections, the wave-vector ratio turns out to be proportional to the spontaneous polarization of one smectic plane:

where

In a more general case Eq. (28) holds and it is necessary to perform a numerical calculation. As a result, in Figs. 3a and 4a the wave-vector ratio as a function of the spontaneous polarization is reported for different values of pre-azimuth F₀ . When F₀ = 0^°, in the initial conditions the tilt director 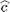is normal to the cell plates; when F₀ = 90^°, the tilt director 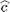lies in the cell plates, and the 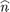-orientation is unidirectional planar. According to the present model, numerical calculations performed on the dispersion relation Eq. (28) demonstrate that the biperiodic pattern is a threshold phenomenon, with the wavelength l_x bonded to the cell thickness in the case of strong anchoring. Above the threshold, the wavelength l_z is almost inversely proportional to the smectic layer spontaneous polarization P_s , and increases with the pre-azimuth as well. In Fig. 3b and 4b a zoom of the origin zone of Figs. 3a and 4a is reported, showing that for pre-azimuth F₀ ~ 0^°, implying pre-tilt close to the smectic tilt q, the transition is of the first order, whereas for pre-azimuth F₀ ~ 90^°, implying a quasi-planar configuration, the transition is of the second order. The first order character yields in the range F₀=0^°-45^°, whereas the second order character yields in the range F₀ = 45^°-90^°. In any case the P_s-threshold diminishes as the pre-azimuth F₀ increases as well, converging to a minimum critical value » 0.2 ues.

III Conclusions

The arising of periodical instability in smectic C^* has been analysed and a new model in the frame of continuum theory has been established. According to our model, a soft mixed bend- and twist- distortion spontaneously arises in homogeneous surface stabilised cells ordered in bookshelf geometry, when the external field is switched off. Such distortion is biperiodical, since the two wave-vectors instead of wave vector and directions instead of direction. In antiferroelectric configuration it can be explained without invoking smectic planes- and layers deformation, as a competition between the coupling of spontaneous polarisation-internal electric field and the Coulombian interaction among charges separated in smectic layers at the cell walls. Such competition is driven by anchoring and is mediated by elasticity. The dielectric- and flexoelectric- contributions just give small corrections to this picture. In the case of strong anchoring, the wave-vector ratio is proportional to the spontaneous polarisation of one smectic plane. However, in the ferroelectric state, such type of biperiodical distortion is hindered.

Acknowledgments

This work was partially supported by European Community in the frame of INCO Copernicus Concerted Action "Photocom", under Contract No. IC15-CT98-0806, and of the BRITE-Euram III TN "LC Photonet". The support of TMR Network "SILC" under Contract No. FMRX-CT98-0209 is also gratefully acknowledged. Two of the authors (S.I.T. and A.S.) fully acknowledge the invitation and the support of Organizing Committee of "5th Ibero-American Workshop on Complex Fluids and Their Application", which allowed them to attend the Workshop. We are grateful to L. Kramer for very useful discussion.

• [1] R.B. Meyer, L. Liebert, L. Strzelecki, and P. Keller, J. Phys (France) 36, L69 (1975).
• [2] N.A. Clark and S.T. Lagerwall, Appl. Phys. Lett. 36, 899 (1980).
• [3] S.T. Lagerwall, Ferroelectric and Antiferroelectric Liquid Crystals, (Wiley-VCH, Weinheim, 1999).
• [4] Yu.P. Panarin, E.P. Pozhidaev, and M.I. Barnik, Mol. Mat. 1, 29 (1992).
• [5] Tadashi Akahane and Atsushi Obinata, Liq. Cryst. 15, 883 (1993) et ref. therein.
• [6] L.A. Beresnev, M.V. Loseva, N.I. Chernova, S.G. Kononov, P.V. Adomenas, and E.P. Pozhidaev, Pisma JETF, 51, 457 (1990).
• [7] L.A. Beresnev, M. Pfelffer, W. Haase, N.I. Chernova, and P.V. Adomenas, Pisma JETF, 53, 170 (1991).
• [8] L. Lejcek and S. Pirkl, Liq. Cryst. 8, 871 (1990).
• [9] J. Pavel and M. Glogarova, Liq. Cryst. 9, 87 (1991).
• [10] R.F. Shao, P.C. Willis, and N.A. Clark, Ferroelectrics 121, 127 (1991).
• [11] V.P. Vorflusev, Yu.P. Panarin, S.A. Pikin, and V.G. Chigrinov, (unpublished).
• [12] J. MacLennan, Europhys. Lett. 13, 435 (1990).
• [13] S.A. Pikin, Mol. Cryst. Liq. Cryst. 215, 73 (1992).
• [14] F.M. Leslie, I.W. Stewart, and M. Nakagawa, Mol. Cryst. Liq. Cryst. 198, 443 (1991).
• [15] I. Dahl, Ferroelectrics 84, 345 (1988).
• [16] C.J. Elston, J.R. Sambles, and M.G. Clark, J. Appl. Phys. 68, 1242 (1990).
• [17] J.C. Jones, E.P. Raynes, M.J. Towler, and J.R. Sambles, Mol. Cryst. Liq. Cryst. 199, 277 (1991).

Publication Dates

• Publication in this collection
  18 Nov 2002
• Date of issue
  June 2002

History

• Received
  30 Jan 2002