Influence of Viscoelastic Properties on the Propagation of Small Amplitude Sound Waves

Influence of Viscoelastic Properties on the Propagation of Small Amplitude Sound Waves

Oscar Sotolongo Costa, Alexei Vázquez Vázquez, and José Marín Antuna

Department of Theoretical Physics

Havana University, Havana 10400, Cuba

Received May 10, 1997

The influence of viscoelastic properties in sound propagation is analyzed. A generalization of Oldroyd viscoelastic model for incompressible solutions is made for the case of compressible fluids, introducing viscoelastic effects in normal stresses. This generalized model allows us to obtain an integro-differential equation for the small oscillations of pressure in the sound wave. The dispersion relations obtained from this equation are valid in any range of frequency and contain as particular case results reported in the literature.

I. Introduction

Viscoelastic models are interesting because they fit quite well the data found in experiments of many polymeric fluids. The simplest model that accounts for viscoelastic properties is the so-called Maxwell model in which only pure viscoelastic effects are included [1]. An extension of Maxwell model that allows to fit data of many polymeric solutions was introduced by Oldroyd [2]. This model is made by the superposition of a Maxwell component and a Newtonian one. More complex models have been proposed in order to obtain frame invariant equations [3,4]. These models account for the viscoelastic behavior of incompressible fluids. They have been successfully used in problems where only shear stresses are important, such as: flow through tubes [5,6], flow trough porous media [7], shear waves [4], convection [8,9], and so on. In this paper we deal with the propagation of sound waves in viscoelastic media, and include the influence of the viscoelastic properties in normal stresses. An extension of Oldroyd model to the case of compressible solutions is made in section II. With this generalized model an integro-differential equation for the small oscillations of pressure in the sound wave is obtained in section III. The dispersion relations derived from this equation are analyzed in section IV.

II. Oldroyd model for compressible solutions

The relation between stress and deformation is the so-called constitutive equation, whose determination in complex fluids (polymers, etc.) is the main object of rheology. A viscoelastic model which describes quite well the behavior of polymeric solutions is the Oldroyd model. In this model the equation of motion can be written as [4]

. (2.1)

where r is the liquid density, h_S is the solvent viscosity characterizing the purely viscous (Newtonian) component of the stress, and t is the viscoelastic extra stress tensor. Here

(2.2)

is the total or substantial time derivative and n = n(r, t) is the velocity in the point r of the fluid at time t .

In Oldroyd model the viscoelastic extra stress tensor is given by the following tensorial generalization of Maxwell model [4]

, (2.3)

where D is the deformation rate tensor defined as

, (2.4)

(2.4) and l₁, h₁ are the shear relaxation time and viscosity, respectively. The symbol T indicates transposition. Then D is the symmetric part of the tensor is a differential operator which is introduced in order to obtain a frame invariant constitutive equation [4]. This operator is not unique, it can be written in the following general form

, (2.5)

where W is the antisimetric part of the tensor , i.e.

, (2.6)

and a is a parameter. The cases a = 1 and a = - 1 corresponds with the lower and upper convected invariant derivatives, respectively, and the case a = 0 with the corrotational rate.

Besides, since in the Oldroyd model the fluid is considered incompressible [4] then the continuity equation is given by

(2.7)

which consequently implies, from Eq. (2.3), that Trt = 0 for t >> l₁.

In order to introduce viscoelastic effects in normal stresses this model is generalized as follows. We will assume that Trt also satisfies Eq. (2.3), but with l₂ and h₂ as the relaxation time and the viscosity associated to normal stresses, i.e.

Trt + l₂dTrt/dt = 2h₂TrD, (2.8)

Here we have used the total derivative instead of the differential operator d/dt because the quantity Trt is a scalar.

On the other hand, if the fluid is compressible the continuity equation is now given by

(2.9)

where the density variations were considered.

The system of equations (2.1, 2.3, 2.8, 2.9) is completed by the equation of state

p = p(r, x) (2.10)

where x may be the temperature or the entropy. If fluctuations of fluid variables like pressure, density and velocity have large periods then the process will takes place under thermal equilibrium and temperature T may be considered constant. In this case a convenient choice is x = T . On the other hand, if they have a very short period the process may be considered adiabatic and, therefore, isoentropic. Now the best choice will be x = s , s been the entropy. In both cases it is obtained that

(2.11)

that is, the pressure only depends on liquid density.

Notice that Eq. (2.11) is only valid in these limit cases. In the general case the fluctuations of x , the temperature for instance, most be taken into account introducing the heat conduction equation. However, in this paper, heat conduction effects are neglected and only viscoalestic processes are considered.

III. Equation for the small oscillations of pressure

The equations presented in the previous section can be linearized when r, p and n perform small oscillations around the equilibrium values r₀ , p₀ and 0, respectively. If T and L are the characteristic time and length of temporal and spatial variations, respectively, and I the mean displacement of the fluid particles in the sound wave, then

, (3.1)

, (3.2)

, (3.3)

, (3.4)

where || || is some norm of second rank tensors.

Thus, if l << L , from these relations and Eqs. (2.2) and (2.5), we have

, (3.5)

, (3.6)

In this approximation the equation of motion is reduced to

. (3.7)

and the equations for shear (2.3) and normal (2.8) stress are now first order linear differential equations. The integration of this equations leads to the linear constitutive relation

, (3.8)

where I is the identity tensor, and

G(t) = (h₁/l₁)exp(-t/l₁), (3.9)

K(

t) = (h

₂/l

₂)exp(-

t/l

₂), (3.10)

are the shear and normal stress relaxation functions, respectively.

Besides, the continuity (2.9) and state (2.11) equations have, in the linear approximation, the form

, (3.11)

, (3.12)

where is the compressibility modulus at constant x .

Now, eliminating t, D , n and r from equations (2.4, 3.7, 3.8, 3.11, 3.12) one obtains

, (3.13)

where

M(s) = K(s) + 4G(s)/3 (3.14)

is the relaxation function of longitudinal stresses. The first term in (3.13) is due to the compressibility of the solution at equilibrium, the second one to the Newtonian component of the solvent, and the last one to the viscoelastic effects in the longitudinal stress, which has some component of shear and normal stresses. In the next section we are going to study the influence of these three terms in the dispersion relations.

IV. Dispersion relations

In order to analyze the frequency dependence of the absorption coefficient and the sound velocity a plane harmonic wave is proposed, i.e. the pressure has the form

p = p₀ + Aexp[i(k . r + wt)], (4.1)

where A is the amplitude of the oscillations around p₀, and w is the cyclic frequency. k , the module of the wave vector, is related to the absorption coefficient a and the sound velocity V through the equation

k = w/V + ia . (4.2)

Substitution of (4.1) into the equation for the small oscillations of pressure (3.13), gives

, (4.3)

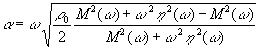
, (4.4)

Here

(4.5)

and

(4.6)

are the frequency dependent longitudinal modulus and viscosity respectively.

Frequently, shear and normal relaxation times are approximately equal. From now on we will assume l₁» l₂ = l. In this approximation the longitudinal modulus (4.5) and viscosity (4.6) are reduced to

, (4.8)

, (4.9)

where

h₀ = h_s + h₂ + 4h₁/3 (4.10)

is the static longitudinal viscosity.

For low frequencies, wl << 1, M(w) » K₀ and h(w) » h₀. So, for frequencies such that K₀ >> wh₀ from (4.3) and (4.4) it is obtained

V ²₀ = K₀/r₀ , (4.11)

a₀ = w²h₀/2r₀V₀³ , (4.12)

which are the expressions for a viscous compressible fluid [11].

At low frequencies the polymer solution behaves like a viscous compressible fluid with compressibility modulus K₀ and a longitudinal viscosity h₀, given by (4.10). In this case the only influence of the added polymer phase is to increase the viscosity of the solution.

On the other hand, for high frequencies, wl >> 1, M(w) » K₀ + (h₀ - h_s)/l and h(w) »= h_s. So, for frequencies such that K₀ + (h₀ - h_s)/l << wh_s from (4.3) and (4.4) it is obtained

, (4.13)

, (4.14)

which corresponds with the behavior of a viscous incompressible fluid at high frequencies [11,12]. At high frequencies the added polymer does not exert any influence on the behavior of the solution. The sound propagation is determined by the solvent viscosity h_s.

At intermediate frequencies, when wl ~ 1 , the longitudinal modulus and viscosity are frequency dependent through Eqs. (4.5) and (4.6), respectively. This is a consequence of viscoelastic effects. At low frequencies the contribution of the polymer is Newtonian according to Eq. (4.6), at high frequencies elastic according to (4.5), and at intermediate frequencies it will be a mixture of both limiting cases. In this region it is necessary to use the general expressions (4.3) and (4.4) for the sound velocity and the absorption coefficient, respectively.

V. Conclusions

The propagation of small amplitude sound waves in an Oldroyd compressible fluid was analyzed. The Oldroyd model for incompressible solutions was generalized to the case of compressible ones, by including viscoelastic effects in normal stress through Eq. (2.8). This paper is original in this aspect.

In the linear approximation the model leads to an integro-differential equation for the small amplitude oscillations of pressure in the sound wave. Three fundamental factors are included: the compressibility of the solution, the Newtonian component due to the solvent, and the viscoelastic contribution due to the polymer, characterized by the relaxation function of longitudinal stress, Eq. (3.12).

The obtained dispersion relations are valid in any range of frequency, which give a great generality to our results. They are given by Eq. (4.3) for the sound velocity and (4.4) for the absorption coefficient. These expressions contain two important limiting cases, at low frequencies the solution behaves like a viscous compressible fluid with compressibility K₀ and longitudinal viscosity h₀, and at high frequencies the behavior of the solution is determined by the Newtonian viscosity of the solvent h_s.

References

1. J. C. Maxwell, Phil. Trans. 157, 69 (1867).

2. J. G. Oldroyd, Proc. Roy Soc. (London) A200, 523 (1950).

3. R. B. Bird, R. C. Amstrong and O. Hassager, Dynamic of Polymeric Fluids Vol. 1, Wiley, New York (1977).

4. D. D. Joseph, Fluid Dynamics of Viscoelastic Liquids, Springer, New York (1990).

5. M. Ahrens, Y. Yoo, and D. D. Joseph, J. Non-Newt. Fluid Mech. 24, 67 (1987).

6. S. Pilitsis and A. N. Beris, J. Non-Newt. Fluid Mech. 31, 231 (1989).

7. J. A. Deiber and W. R. Schowalter, AIChE J. 27, 912 (1981).

8. G. E. Karniadakis, Inter. J. Heat and Mass Transfer 31, 107 (1988).

9. J. Martinez, Internal Report 5, Univ. Navarra, Spain (1991)

10. A. Vázquez Vázquez, O. Sotolongo Costa, and J. Marí n Antuña, Procedings of the III CCFD and III LASFM, Caracas (1995).

11. L. Landau and E. Lifchitz, Fluid Mechanics, Nauka, Moscow (1971).

12. J. Marín Antuna and O. Sotolongo Costa, Rev. Cub. Fis. 11, 13 (1991).

Publication Dates

• Publication in this collection
  04 Feb 1999
• Date of issue
  Sept 1997

History

• Received
  10 May 1997