On properness of minimal surfaces with bounded curvature

On properness of minimal surfaces with bounded curvature

Gregório P. Bessa; Luquésio P. M. Jorge

Departamento de Matemática, Universidade Federal do Ceará 60455-760 Fortaleza, CE, Brasil

^{Correspondence}

ABSTRACT

We show that immersed minimal surfaces in the euclidean 3-space with bounded curvature and proper self intersections are proper. We also showthat restricted to wide components the immersing map is always proper, regardless the map being proper or not. Prior to these results it was only known that injectively immersed minimal surfaces with bounded curvature were proper.

Key words: Proper immersion, bounded curvature, proper self intersections.

RESUMO

Mostramos que as superfícies mínimas imersas no espaço euclideano de dimensão três, com curvatura limitada e autointersecções próprias, são próprias. Mostramos também que restrita às componentes amplas, a imersão é própria, independentemente do fato de ser a imersão inicial própria ou não. Antes destes resultados, era apenas conhecido que as imersões injetivas, mínimas, completas, com curvatura limitada, eram próprias.

Palavras-chave: imersão própria, curvatura limitada, autointersecções próprias.

1. INTRODUCTION

Most of the results about the structure of complete minimal surfaces of 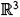requires the hypothesis that the surfaces are proper. It would be an interesting problem to determine what geometries imply that a complete minimal surface of

is proper. The first result, (to the best of our knowledge), toward this problem is due to Rosenberg (Rosenberg 2000). He proved that an injectively immersed complete minimal surface of 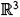with bounded sectional curvature is proper. On the other extreme, there are examples of complete non proper minimal surfaces of 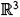with bounded sectional curvature, whose closures are dense in large subsets of 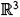, (Andrade 2000). These examples show that bounded sectional curvature alone is not enough to make a minimal immersion proper but the failure happens in what can be considered as ''pathological'' examples.

The key to understand these phenomena are the self intersections. In Andrade's examples they have accumulation points, in contrast to injectively immersed surfaces that are not self intersecting. In the middle of these two cases there are many known examples of proper complete minimal surfaces with bounded sectional curvature self intersecting ''properly''. Our first result, Theorem 1.2, explains the (non)properness of these examples above in terms of their self intersections. To give its precise statement we need the following definition.

DEFINITION 1.1. An isometric immersion j : M ® 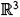is said to have proper self intersections if the restriction of j to G = j^–1(L) is a proper map, where L = {x Î 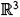; # (j^–1(x)) > 2} .

THEOREM 1.2. An isometric minimal immersion j : M ® 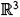of a complete surface with bounded sectional curvature and with proper self intersections is proper.

There is another way that one can extend Rosenberg's result. Among the connected components of M \ G, one type is called wide component, and it is possible to show that restricted to a wide component the immersing map is proper. Moreover, when the immersing map is injective the whole surface is a wide component.

DEFINITION 1.3. A connected component M' of M \ G is wide if for divergent sequence of points x_kÎ M' with j(x_k) converging in

there is a sequence of positive real numbers r_k ® ¥ such that the geodesic balls B_M(x_k,r_k) of M centered at x_k with radius r_k are contained in M'. Otherwise we say that the connected component is narrow.

THEOREM 1.4. Let j : M ® 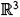be an isometric minimal immersion of a complete surface with bounded sectional curvature. Then the restriction of j to any wide component M' of M \ G is proper.

Theorem 1.4 has a slight more general version which shows the role that the set G plays in the properness problem.

THEOREM 1.5. Let j : M ® 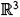be an isometric minimal immersion of a complete surface with bounded sectional curvature. There is no divergent sequence of points x_kÎ M with j(x_k) converging in

and dist_M(x_k, G) ® ¥.

We shall finish this introduction presenting some questions related to this work that we think are of importance.

QUESTION 1.6. Let j : M ® 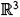be an isometric minimal immersion of a complete surface with bounded curvature. Let S Ì Limj be a limit leaf. Can S be injectively immersed? Or can S have an injectively immersed end?

The definitions of Limj and limit leaf are given below in the preliminaries. The negative answer would be an indicative that Limj is generated by accumulation points of j|_G. Related to Question 1.6 one can ask, when Limj is generated by Limjj_|G and when it is not?

QUESTION 1.7. Let j : M ® 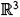be a non proper isometric minimal immersion of a complete surface with bounded curvature. Does M \ G have wide connected components?

The non existence of wide components in M \ G would suggest that M is included in the Limj. Unfortunately there are not enough examples to understand what happens.

Finally, it is important to know when a minimal immersion of M is an O-minimal set or not. O-minimal structures have been studied in algebraic geometry by many people such as L. Bröker, M. Coste, L. Van Den Dries and others (see Van Den Dries 1980). The following question, if answered positively, would imply that a minimal immersion with bounded curvature is an O-minimal set.

QUESTION 1.8. Let j : M ® 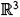be a non proper isometric minimal immersion of a complete surface with bounded curvature. Does the intersection of M with one line of

have only finite connected components?

2. PRELIMINARIES

One of the reasons of the properness requirement in most structure results in minimal surface theory is the absence of tools applicable for non proper minimal immersions. To remedy this situation we introduced in (Bessa and Jorge 2001) the notion of limit sets of an isometric immersion. The limit sets of non proper isometric minimal immersions into 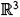with bounded curvature have a rich structure that can be used to better understand those type of immersions. Here in this section, we recall its definition and state the results needed in the the sequel.

DEFINITION 2.1. Let j : M ® N, be an isometric immersion where M and N are complete Riemannian manifolds. The set of all points p Î N such that there exists a divergent sequence {p_l} Ì M so that j(p_l) ® p in N is called the limit set of j, denoted by Limj, i.e.

Limj = {p Î N; ${p_l} Ì M, dist_M(p₀, p_l) ® ¥ nd dist_N(p, j(p_l)) ® 0}

The following theorem about limit set was proved in (Bessa and Jorge 2001) in a more general situation than this version here presented.

THEOREM 2.2. Let j : M ® 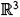be a non proper isometric minimal immersion of a complete surface with bounded sectional curvature. Then for each point p Î Limj there is a family of complete immersed minimal surfaces S_lÌ Lim j, with bounded sectional curvature, containing p, (p Î S_l). Each of these surfaces S_l is called a limit leaf passing through p.

REMARK 2.3. The idea of a proof for this theorem is the following: Since the immersing map j is non proper, there is a divergent sequence of points x_k in M with j(x_k) converging to a point p in 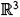. By the fact that the immersion is minimal, the surface has bounded sectional curvature and the ambient space¹ is 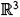, there is a sequence of disjoint disks D_k Ì M with radius uniformly bounded from below containing x_k such that j(D_k) are minimal graphs over their tangent spaces at j(x_k), also with radius uniformly bounded from below. These graphs converge, up to subsequences, to a minimal graph D with bounded curvature, containing p. Each point q of D is limit of a sequence of points j(q_k) Î j(D_k). This limit graph extends to a complete minimal surface with bounded curvature S Ì Lim j called limit leaf. One can see that given a compact K Ì S, there are a sequence of compacts K_k Ì j(M) converging (locally as graphs) to K.

In (Bessa et al. 2001) was proved the following theorem.

THEOREM 2.5. Let j : Mⁿ

Nⁿ⁺¹ be a complete minimal immersed hypersurface with scalar curvature bounded from below in a complete n + 1 dimensional Riemannian manifold N with bounded geometry. Suppose in addition that N has non negative Ricci curvature Ric_N> 0. Then j is proper or every orientable leaf S Ì Limj such that S Ç j(M) = Æ is stable. Moreover, if S is compact then S is totally geodesic and the Ricci curvature of N is identically zero in the normal directions to S.

In this note, we observe that one can have a slight improvement in Theorem 2.5. It is possible to allow certain kind of intersections between S and j(M) keeping the same conclusions. To explain better what kind of intersections we can allow, let us define proper intersections.

DEFINITION 2.4. Let j_i : M_i

N be isometric immersions, i = 1,2. We say that the intersection L = j₁ (M₁) Ç j₂(M₂) is proper if the restrictions of j_i to G_i =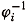 (L)) is a proper map.

REMARK 2.6. Theorem 2.5 is still true if the intersection S Ç j(M) is proper. The proof of Theorem 2.5 needs the hypothesis S Ç j(M) = Æ only to guarantee that S has no self intersections (see Theorem 1.5 and its proof in (Bessa et al. 2001)). This is also obtained if the intersection S Ç j(M) is proper. Otherwise, if S has self intersection in a point p Î S then there are two disks D_i Ì S, i = 1,2, both containing p and intersecting themselves transversally. Each disk D_i is limit of disks Ì j(M). For large indexes j, these disks intersect S at points Î Ç S. These intersection points converge to p and their inverse image are going to infinity in M, showing that the intersection of S and j(M) is non proper.

REMARK 2.7. In Theorem 2.5, when N º 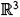then the stability of S implies that S is a plane, (Do Carmo and Peng 1979), (Fisher-Colbrie and Schoen 1980). More generally, when n = 2 the stability of S implies that S is totally geodesic also in the non compact case, (Schoen 1983).

3. PROOF OF THEOREMS 1.2, 1.4 and 1.5

PROOF OF THEOREM 1.5.

Suppose we have a divergent sequence of points x_k Î M with j(x_k) converging to a point p Î 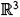and dist_M(x_k, G) ® ¥. For each x_k, consider an open disk D_k centered at x_k with radius dist_M(x_k, G). The sequence j(D_k) converges to a complete limit leaf S of Limj passing by p. Suppose (by contradiction) that there is q Î S Ç j(M). By Remark 2.3 there is a sequence of points y_k Î D_k, with dist(x_k, y_k) < dist(p, q) + 1 such that j(y_k) ® q. For large indices, the disks D(y_k,1) Ì D_k centered at y_k with radius 1 are such that j(D(y_k, 1)) converges in a C² topology to a disc in S centered at q with a radius near 1, thus they intersect j(M) transversally, showing that D_k Ç G ¹ Æ, contradiction. Therefore S Ç j(M) = Æ. This leads to another contradiction, because by Theorem 2.5 or the Strong Half Space Theorem, S and j(M) are parallel planes and proper.

PROOF OF THEOREM 1.2.

If the statement of Theorem 1.2 is not true then by Theorem 1.5, there is a divergent sequence x_k Î M such that j(x_k) converges to a point p Î 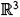and

r = dist(x_k, G) < ¥.

Let y_k Î G a sequence of points realizing the distance dist(x_k, G). Passing to a subsequence if necessary we may say that dist (x_k, y_k) < r + 1. Then y_k Î G is a divergent sequence and j(y_k) Î (p, r + 1). This contradicts the properness of j|_G.

PROOF OF THEOREM 1.4.

Suppose that j restricted to a wide component M' Ì M \ G is not proper. Let x_k Î M' be a divergent sequence such that j(x_k) converges to a point p Î 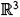. By Theorem 1.5, we have that

dist(x_k, ¶M') < ¥

but by the definition of wide component this can not be.

ACKNOWLEDGMENTS

G.P.B's work was partially supported by CAPES-PROCAD GRANT # 0188/00-0 and L.P.M.J's work was partially supported by CAPES GRANT # BEX2067/00-5.

Manuscript received on February 27, 2003; accepted for publication on June 8, 2003; presented by MANFREDO DO CARMO

• ANDRADE FP. 2000. A wild minimal plane in ³. Proc Amer Math Soc 128: 1451-1457.
• BESSA GP AND JORGE LP. 2001. Limit set structure of isometric immersions. Preprint.
• BESSA GP, JORGE LP AND OLIVEIRA-FILHO G. 2001. Half-Space Theorems for Minimal Surfaces with Bounded Curvature. J Differential Geom 57: 493-508.
• DO CARMO M AND PENG CK. 1979. Stable complete minimal surfaces in ³ are planes. Bull Amer Math Soc 1: 903-905.
• FISHER-COLBRIE AND SCHOEN R. 1980. The Structure of complete stable minimal surfaces in 3-manifolds of non-negative scalar curvature. Comm Pure Appl Math 33: 199-211.
• ROSENBERG H. 2000. A complete embedded minimal surface in ³ of bounded curvature is proper. Unpublished.
• SCHOEN R. 1983. Estimates for stable minimal surfaces in three dimensional manifolds. Ann of Math Stud 103: 111-126.
• VAN DEN DRIES L. 1980. O-minimal structures and real analytic geometry. Current Developments in Mathematics, International Press, 105-152.

1

The ambient space need to have bounded geometry, meaning sectional curvature bounded from above and injectivity radius bounded from below.

Publication Dates

• Publication in this collection
  25 Aug 2003
• Date of issue
  Sept 2003

History

• Received
  27 Feb 2003
• Accepted
  28 June 2003